六年级下册数学北师大版1.3圆柱的体积(课件)(共79张PPT)
文档属性
| 名称 | 六年级下册数学北师大版1.3圆柱的体积(课件)(共79张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 13:26:29 | ||
图片预览






文档简介
(共79张PPT)
第一单元 · 圆柱与圆锥
1.3 圆柱的体积
北京师范大学出版社 六年级 | 下册
什么叫物体的体积?你会计算下面哪些图形的体积?
知识回顾
√
√
5cm
4cm
2.5cm
4cm
4cm
4cm
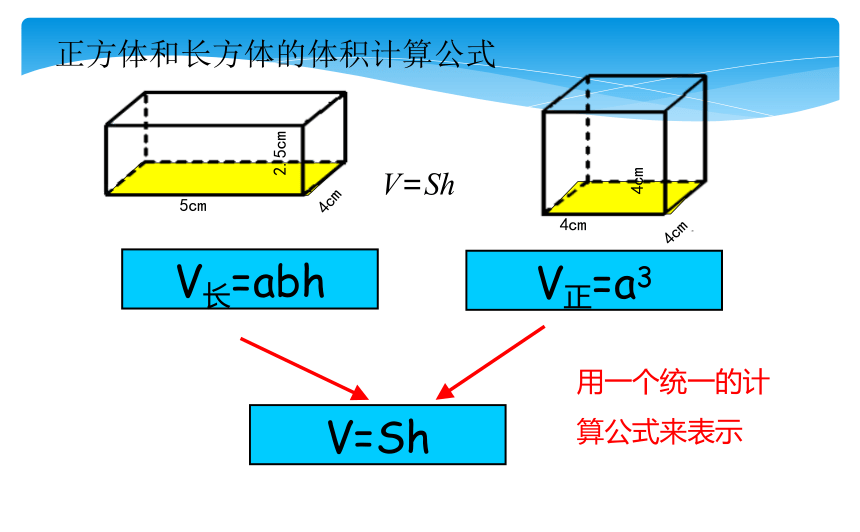
V长=abh
V正=a3
V=Sh
V=Sh
用一个统一的计算公式来表示
正方体和长方体的体积计算公式
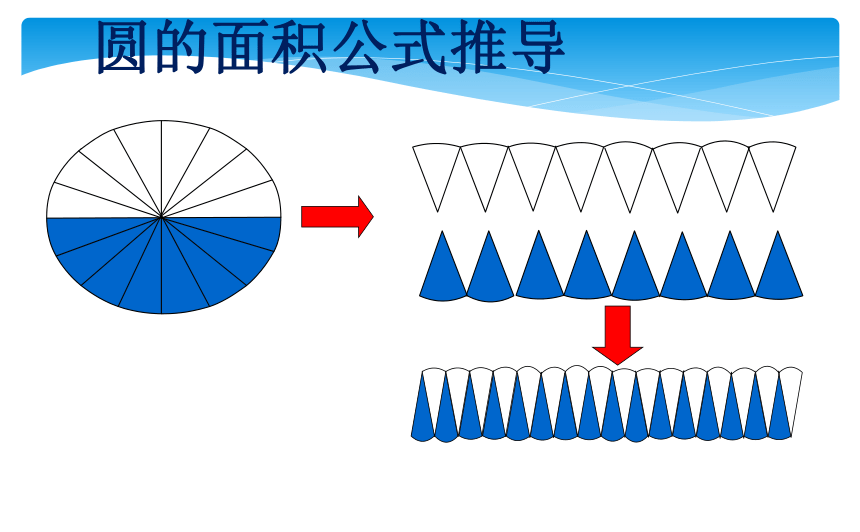
圆的面积公式推导
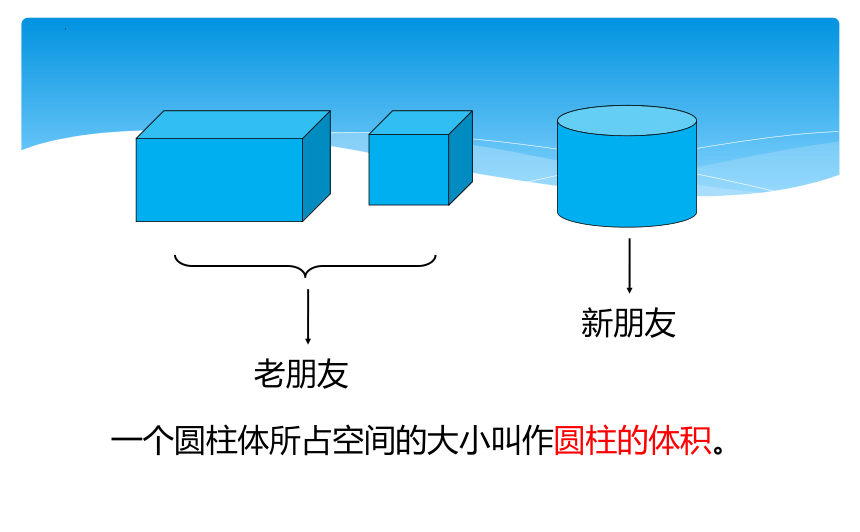
老朋友
新朋友
一个圆柱体所占空间的大小叫作圆柱的体积。
新知探究
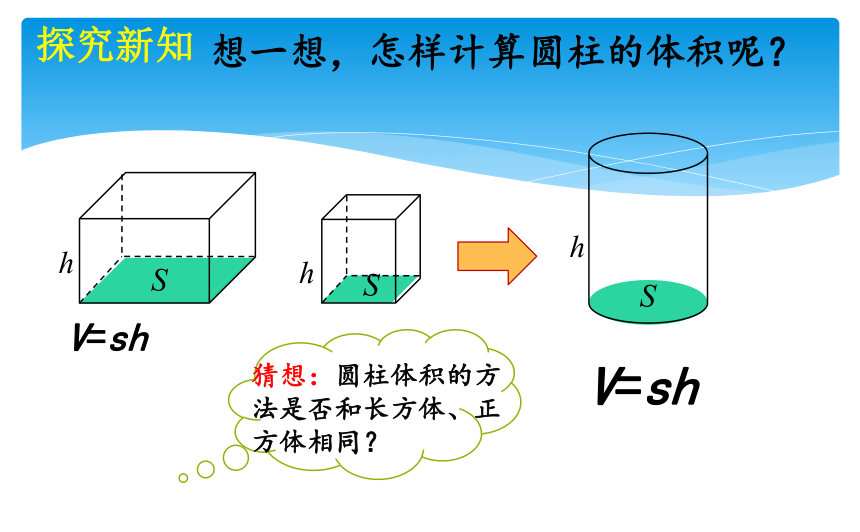
想一想,怎样计算圆柱的体积呢?
V=sh
V=sh
猜想:圆柱体积的方法是否和长方体、正方体相同?
探究新知
圆柱的体积=底面积×高
实践探究
探究问题:
①圆柱的体积与拼成后的长方体的体积有什么关系
②长方体的底面积与圆柱的底面积有什么关系
③长方体的高与圆柱体的高有什么关系?
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
高
长方体的体积=底面积 ×高
圆柱体的体积=
×
底面积
为了推导圆柱的体积,我们可以将圆柱转化为( ),长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( ),长方体的体积等于圆柱的( )。
因为长方体的体积=( )×( ),所以圆柱的体
积=( )×( )。
长方体
底面积
高
体积
底面积
高
底面积
高
新知总结
http://www.lspjy.com/
http://www.lspjy.com/
V圆柱=S× h
= × h
3号
4号
5号
d=10cm
h=9cm
r=3cm
h=9cm
C=18.84cm
h=12cm
V=706.5立方厘米
V=254.34立方厘米
V=339.12立方厘米
高
圆柱体的体积=
×
底面积
已知r和h
V=
× h
高
圆柱体的体积=
×
底面积
已知d和h
V=
× h
高
圆柱体的体积=
×
底面积
已知C和h
V=
×h
V =S h
体积 = 底面积×高
祖暅定理
V =S h
体积 = 底面积×高
幂势即同,则积不容异
横截面
高
祖暅定理
著名的“祖暅原理”,由祖冲之的儿子祖暅,总结了刘徽的有关工作,祖暅应用这个原理,解决了刘徽尚未解决的球体积公式。
该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年。
(1)圆柱体的底面积越大,它的体积越大。
( )
(2)圆柱体的高越长,它的体积越大。
( )
(3)圆柱体的体积与长方体的体积相等。
( )
(4)圆柱体的底面直径和高可以相等。
( )
判一判
做中学:把一张长5厘米、宽4厘米的长方形纸分别绕它的长和宽旋转一周(如下图),形成两个圆柱。
3.14×42×5=251.2(m3)
3.14×52×4=314(m3)
314>251.2
答:绕宽旋转一周形成的圆柱体积大。
做中学:把一张长5厘米、宽4厘米的长方形纸,横着卷成圆柱形,再竖着卷成圆柱形。
3.14×(5÷3.14÷2)2×4
≈7.96(m3)
7.96>6.37
答:横着卷形成的圆柱体积大。
3.14×(4÷3.14÷2)2×5
≈6.37(m3)
做中学:下面的长方体和圆柱哪个体积大?说说你的比较方法
4×4=16(dm2)
3.14×22=12.56(m2)
16>12.56
答:长方体的体积大。
体积变形:求小铁块的体积
2cm
2cm
10cm
3.14×(10÷2)2×2
=157(cm3)
体积变形:将一个棱长为6分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱有多长
6×6×6=216(dm3)
3.14×32=28.26(dm2)
216÷28.26≈7.64(dm)
体积变形:把一个棱长6分米的正方体木块切削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?
3.14×(6÷2)2×6
=3.14×9×6
=175.84(dm3)
1.(基础题)想一想,填一填。
(1)7.8米3=( )分米3
3升56毫升=( )毫升=( )立方厘米
7800
(2)一个圆柱形水杯(水杯厚度忽略不计),它的底面
积是10 cm2,高是12 cm,则这个水杯可以装水
( )升。
0.12
3056
3056
(3)一个圆柱的体积是62.8立方厘米,底面半径是
2厘米,则高是( )厘米。
5
2.(易错题)我是聪明的小法官。
(1)正方体、长方体和圆柱的体积都等于底面积
乘高。 ( )
√
(2)底面直径是4厘米的圆柱,其体积和侧面积一
样大。 ( )
×
(3)一个圆柱的高扩大到原来的2倍,底面半径缩小
到原来的 ,体积不变。 ( )
×
1、把一块长31.4厘米,宽20厘米,高4厘米的长方体钢坯锻造成底面积是50.24平方厘米的圆柱形钢材,这根钢材长多少厘米
2、两个底面积相等的圆柱体,其中一个高为4.5 dm,体积为81 dm3;另一个高为3 dm, 求它的体积。
3、把一个棱长为6分米的正方体木块削成一个最大的圆柱,这个圆柱的体积是多少立方分米
4、一个圆柱,如果把它的高截短3厘米,它的表面积减少94.2平方厘米,那么它的体积减小多少立方厘米
3.(重点题)把一块长31.4厘米,宽20厘米,高4
厘米的长方体钢坯锻造成底面积是50.24平方
厘米的圆柱形钢材,这根钢材长多少厘米
31.4×20×4÷50.24=50(厘米)
答:这根钢材长50厘米。
4.(难点题)两个底面积相等的圆柱体,其中一
个高为4.5 dm,体积为81 dm3;另一个高为3 dm,
求它的体积。
81÷4.5×3=54(dm3)
答:它的体积是54 dm 。
5.(探究题)把一个棱长为6分米的正方体木块
削成一个最大的圆柱,这个圆柱的体积是多少
立方分米
3.14×(6÷2)2×6=169.56(立方分米)
答:这个圆柱的体积是169.56立方分米。
6.(创新题)一个圆柱,如果把它的高截短3厘
米,它的表面积减少94.2平方厘米,那么它的
体积减小多少立方厘米
3.14×(94.2÷3÷3.14÷2)2×3=235.5(立方厘米)
答:它的体积减少235.5立方厘米。
知道S和h:
知道r和h:
知道d和h:
知道C和h:
V=Sh
V=πr2×h
V=(C÷π÷2)2×h
课堂总结
圆柱的体积公式
第一单元 · 圆柱与圆锥
1.3 圆柱的体积
北京师范大学出版社 六年级 | 下册
什么叫物体的体积?你会计算下面哪些图形的体积?
知识回顾
√
√
5cm
4cm
2.5cm
4cm
4cm
4cm
V长=abh
V正=a3
V=Sh
V=Sh
用一个统一的计算公式来表示
正方体和长方体的体积计算公式
圆的面积公式推导
老朋友
新朋友
一个圆柱体所占空间的大小叫作圆柱的体积。
新知探究
想一想,怎样计算圆柱的体积呢?
V=sh
V=sh
猜想:圆柱体积的方法是否和长方体、正方体相同?
探究新知
圆柱的体积=底面积×高
实践探究
探究问题:
①圆柱的体积与拼成后的长方体的体积有什么关系
②长方体的底面积与圆柱的底面积有什么关系
③长方体的高与圆柱体的高有什么关系?
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
底面积
长方体的体积=底面积 × 高
高
长方体的体积=底面积 ×高
圆柱体的体积=
×
底面积
为了推导圆柱的体积,我们可以将圆柱转化为( ),长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( ),长方体的体积等于圆柱的( )。
因为长方体的体积=( )×( ),所以圆柱的体
积=( )×( )。
长方体
底面积
高
体积
底面积
高
底面积
高
新知总结
http://www.lspjy.com/
http://www.lspjy.com/
V圆柱=S× h
= × h
3号
4号
5号
d=10cm
h=9cm
r=3cm
h=9cm
C=18.84cm
h=12cm
V=706.5立方厘米
V=254.34立方厘米
V=339.12立方厘米
高
圆柱体的体积=
×
底面积
已知r和h
V=
× h
高
圆柱体的体积=
×
底面积
已知d和h
V=
× h
高
圆柱体的体积=
×
底面积
已知C和h
V=
×h
V =S h
体积 = 底面积×高
祖暅定理
V =S h
体积 = 底面积×高
幂势即同,则积不容异
横截面
高
祖暅定理
著名的“祖暅原理”,由祖冲之的儿子祖暅,总结了刘徽的有关工作,祖暅应用这个原理,解决了刘徽尚未解决的球体积公式。
该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年。
(1)圆柱体的底面积越大,它的体积越大。
( )
(2)圆柱体的高越长,它的体积越大。
( )
(3)圆柱体的体积与长方体的体积相等。
( )
(4)圆柱体的底面直径和高可以相等。
( )
判一判
做中学:把一张长5厘米、宽4厘米的长方形纸分别绕它的长和宽旋转一周(如下图),形成两个圆柱。
3.14×42×5=251.2(m3)
3.14×52×4=314(m3)
314>251.2
答:绕宽旋转一周形成的圆柱体积大。
做中学:把一张长5厘米、宽4厘米的长方形纸,横着卷成圆柱形,再竖着卷成圆柱形。
3.14×(5÷3.14÷2)2×4
≈7.96(m3)
7.96>6.37
答:横着卷形成的圆柱体积大。
3.14×(4÷3.14÷2)2×5
≈6.37(m3)
做中学:下面的长方体和圆柱哪个体积大?说说你的比较方法
4×4=16(dm2)
3.14×22=12.56(m2)
16>12.56
答:长方体的体积大。
体积变形:求小铁块的体积
2cm
2cm
10cm
3.14×(10÷2)2×2
=157(cm3)
体积变形:将一个棱长为6分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱有多长
6×6×6=216(dm3)
3.14×32=28.26(dm2)
216÷28.26≈7.64(dm)
体积变形:把一个棱长6分米的正方体木块切削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?
3.14×(6÷2)2×6
=3.14×9×6
=175.84(dm3)
1.(基础题)想一想,填一填。
(1)7.8米3=( )分米3
3升56毫升=( )毫升=( )立方厘米
7800
(2)一个圆柱形水杯(水杯厚度忽略不计),它的底面
积是10 cm2,高是12 cm,则这个水杯可以装水
( )升。
0.12
3056
3056
(3)一个圆柱的体积是62.8立方厘米,底面半径是
2厘米,则高是( )厘米。
5
2.(易错题)我是聪明的小法官。
(1)正方体、长方体和圆柱的体积都等于底面积
乘高。 ( )
√
(2)底面直径是4厘米的圆柱,其体积和侧面积一
样大。 ( )
×
(3)一个圆柱的高扩大到原来的2倍,底面半径缩小
到原来的 ,体积不变。 ( )
×
1、把一块长31.4厘米,宽20厘米,高4厘米的长方体钢坯锻造成底面积是50.24平方厘米的圆柱形钢材,这根钢材长多少厘米
2、两个底面积相等的圆柱体,其中一个高为4.5 dm,体积为81 dm3;另一个高为3 dm, 求它的体积。
3、把一个棱长为6分米的正方体木块削成一个最大的圆柱,这个圆柱的体积是多少立方分米
4、一个圆柱,如果把它的高截短3厘米,它的表面积减少94.2平方厘米,那么它的体积减小多少立方厘米
3.(重点题)把一块长31.4厘米,宽20厘米,高4
厘米的长方体钢坯锻造成底面积是50.24平方
厘米的圆柱形钢材,这根钢材长多少厘米
31.4×20×4÷50.24=50(厘米)
答:这根钢材长50厘米。
4.(难点题)两个底面积相等的圆柱体,其中一
个高为4.5 dm,体积为81 dm3;另一个高为3 dm,
求它的体积。
81÷4.5×3=54(dm3)
答:它的体积是54 dm 。
5.(探究题)把一个棱长为6分米的正方体木块
削成一个最大的圆柱,这个圆柱的体积是多少
立方分米
3.14×(6÷2)2×6=169.56(立方分米)
答:这个圆柱的体积是169.56立方分米。
6.(创新题)一个圆柱,如果把它的高截短3厘
米,它的表面积减少94.2平方厘米,那么它的
体积减小多少立方厘米
3.14×(94.2÷3÷3.14÷2)2×3=235.5(立方厘米)
答:它的体积减少235.5立方厘米。
知道S和h:
知道r和h:
知道d和h:
知道C和h:
V=Sh
V=πr2×h
V=(C÷π÷2)2×h
课堂总结
圆柱的体积公式
