华东师大版七年级数学上册 5.2.2 平行线的判定课件(共24张PPT)
文档属性
| 名称 | 华东师大版七年级数学上册 5.2.2 平行线的判定课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 16:34:22 | ||
图片预览




文档简介
(共24张PPT)
第5章相交线与平行线
华东师大版七年级上册
5.2.2平行线的判定
知识和技能
掌握平行线的判定方法
过程与方法
经历探究直线平行的条件的过程,掌握直线平行的条件
情感态度与价值观
经历观察、操作、交流等活动,进一步发展空间观念和推理能力
学习目标:
问题1
两条不重合的直线的位置关系有哪几种?
问题2
怎样的两条直线平行?
问题3
上节课你学了平行线的哪些内容?
相交(包括垂直)和平行两种.
在同一平面内,不相交的两条直线平行.
2. 如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
1. 经过直线外一点,有且只有一条直线与已知直线平行.
知识回顾:
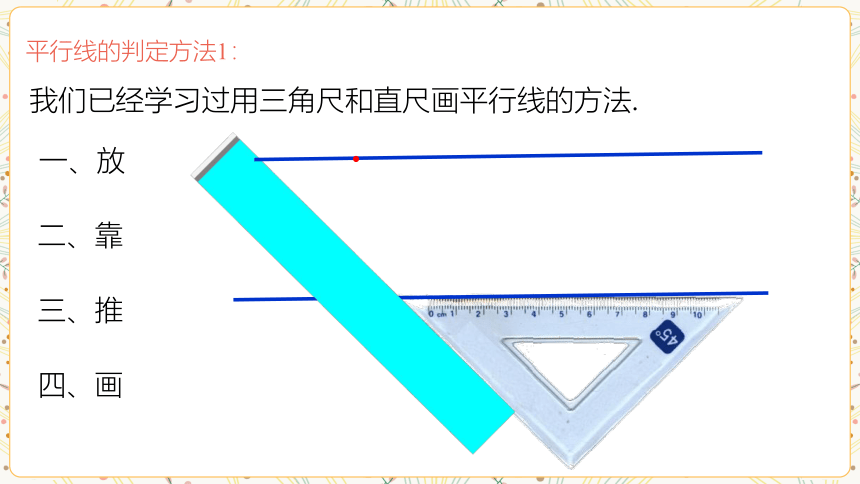
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
●
平行线的判定方法1:
b
A
2
1
a
B
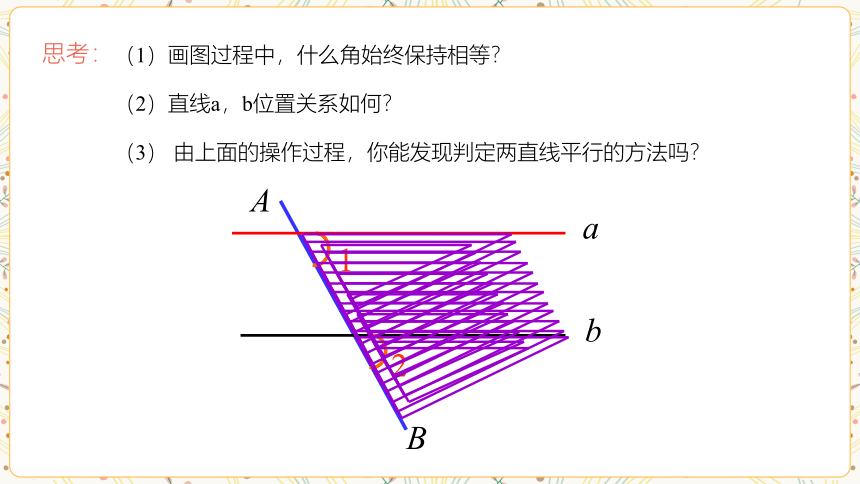
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
(3) 由上面的操作过程,你能发现判定两直线平行的方法吗?
思考:
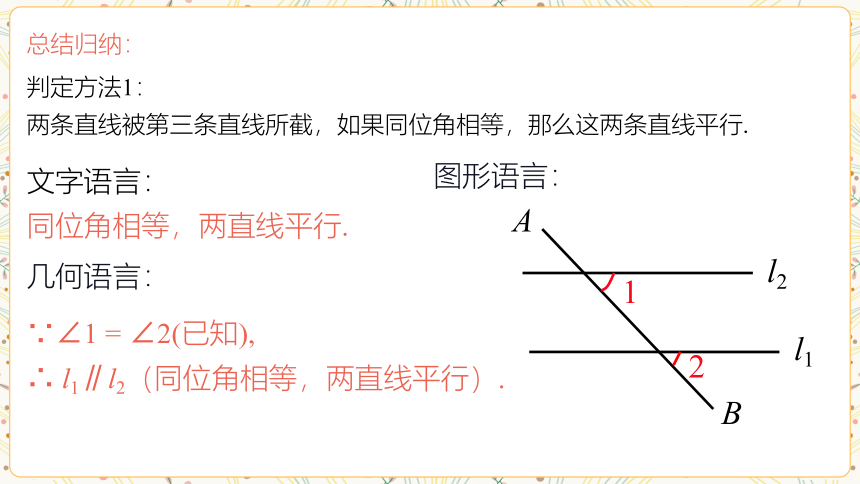
判定方法1:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
文字语言:
同位角相等,两直线平行.
几何语言:
∵∠1 = ∠2(已知),
∴ l1∥l2(同位角相等,两直线平行).
1
2
l2
l1
A
B
总结归纳:
图形语言:
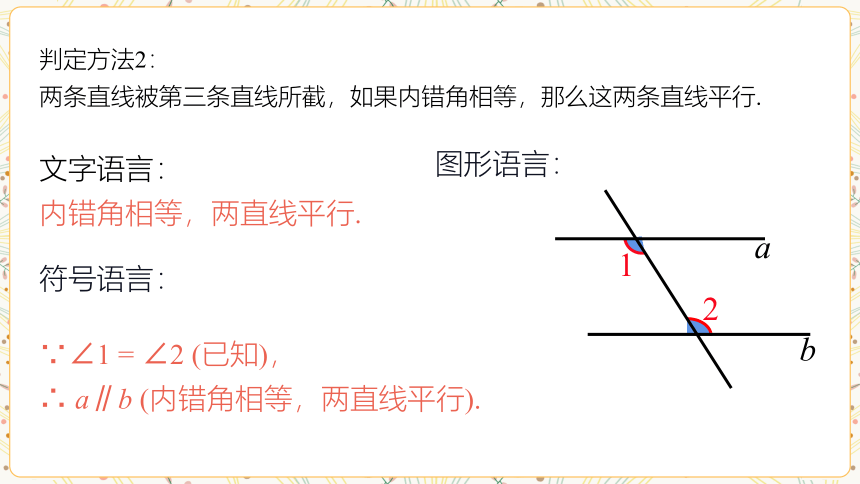
判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
文字语言:
内错角相等,两直线平行.
∵∠1 = ∠2 (已知),
∴ a∥b (内错角相等,两直线平行).
符号语言:
2
b
a
1
图形语言:
判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
文字语言:
同旁内角互补,两直线平行.
符号语言:
2
b
a
1
∵∠1 + ∠2 = 180° (已知),
∴ a∥b (同旁内角互补,两直线平行).
图形语言:
根据图形填空:
(1) (已知)
____//____(内错角相等,两直线平行)
(2) (已知)
____//____(__________________________)
同旁内角互补,两直线平行
(3) (已知)
____//____(__________________________)
(4) (已知)
____//____(_________________________).
同位角相等,两直线平行
小试牛刀:
CF
CF
AD
AD
BC
BC
DE
DE
同旁内角互补,两直线平行
思考:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
理由:
∵ b⊥a,c⊥a(已知),
∴ ∠1 =∠2 = 90°(垂直定义).
∴ b∥c(同位角相等,两直线平行).
小组讨论并思考:
你还能利用其他方法说明 b∥c 吗?
a
b
c
1
2
在同一平面内,垂直于同一条直线的两条直线平行.
大展身手:
1.如图:如果∠1=∠2,那么AB//CD,其依据可以简单说成( )
D
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
2.如图:∠1=120°,要使a//b,则∠2的大小是( )
A.60°
B.80°
C.100°
D.120°
D
3.如图:工人师傅在工程施工中,需要在同一平面内弯制一个变形
管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB//BC
B.BC//CD
C.AB // DC
D.AB与CD相交
C
4.下列画出的直线a与直线b不一定平行的是( )
C
5.如图:若 与 互补,与互补,则一定有( )
B
B.
C. D.
6.如图:若 ,则____//____;若 ,则____//____.
7.如图: 和 分别为直线 与直线
和 相交所成的角.如果 那
么当 ____时,可判定 .
第5题图
8.小明把一副三角板摆放在桌面上,如图所示,其中边
, 在同一条直线上,可以得到____//____,依据是
________________________.
内错角相等,两直线平行
AC
DE
9.如图:已知 于点 于点 .试说明: .
解: (已知),
(____________).
同理, .
(__________),
即 .
(已知),
____(__________).
____//____(________________________).
垂直的定义
等量代换
等量代换
内错角相等,两直线平行
∠4
DF
AE
10.如图,已知 平分 , 平分 ,
且 与 互余.试说明: .
解: 与 互余,
.
平分 , 平分 ,
, .
.
.
11.如图①,∠B=25°,∠D=42°,∠BCD=67°,试判断AB和DE的位置关系,并说明理由。
解:AB//DE
过点C向右作∠BCF=25°,则∠BCF=∠B,
∴AB//CF则∠DCF=∠BCD-∠BCF= 67°-25°
=42°所以________________________.
(1)请补充上述解题过程。
∴∠DCF=∠D,∴CF//ED,∴AB
(2)如图②,∠1=120°,∠2=150°,AE⊥EC,试判断AB,CD的 位置关系,并说明理由。
(2)AB//CD
如图②,过点E向右作∠AEF=60°
∵∠1=120°
∴∠1+∠AEF=180°
∴AB//EF
∵AE⊥EC,∴∠AEC=90°
∴∠FEC=90°—60°=30°
∵∠2=150°
∴∠FEC+∠2=180°
∴EF // CD
∴AB // CD
第5章相交线与平行线
华东师大版七年级上册
5.2.2平行线的判定
知识和技能
掌握平行线的判定方法
过程与方法
经历探究直线平行的条件的过程,掌握直线平行的条件
情感态度与价值观
经历观察、操作、交流等活动,进一步发展空间观念和推理能力
学习目标:
问题1
两条不重合的直线的位置关系有哪几种?
问题2
怎样的两条直线平行?
问题3
上节课你学了平行线的哪些内容?
相交(包括垂直)和平行两种.
在同一平面内,不相交的两条直线平行.
2. 如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
1. 经过直线外一点,有且只有一条直线与已知直线平行.
知识回顾:
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
●
平行线的判定方法1:
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
(3) 由上面的操作过程,你能发现判定两直线平行的方法吗?
思考:
判定方法1:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
文字语言:
同位角相等,两直线平行.
几何语言:
∵∠1 = ∠2(已知),
∴ l1∥l2(同位角相等,两直线平行).
1
2
l2
l1
A
B
总结归纳:
图形语言:
判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
文字语言:
内错角相等,两直线平行.
∵∠1 = ∠2 (已知),
∴ a∥b (内错角相等,两直线平行).
符号语言:
2
b
a
1
图形语言:
判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
文字语言:
同旁内角互补,两直线平行.
符号语言:
2
b
a
1
∵∠1 + ∠2 = 180° (已知),
∴ a∥b (同旁内角互补,两直线平行).
图形语言:
根据图形填空:
(1) (已知)
____//____(内错角相等,两直线平行)
(2) (已知)
____//____(__________________________)
同旁内角互补,两直线平行
(3) (已知)
____//____(__________________________)
(4) (已知)
____//____(_________________________).
同位角相等,两直线平行
小试牛刀:
CF
CF
AD
AD
BC
BC
DE
DE
同旁内角互补,两直线平行
思考:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
理由:
∵ b⊥a,c⊥a(已知),
∴ ∠1 =∠2 = 90°(垂直定义).
∴ b∥c(同位角相等,两直线平行).
小组讨论并思考:
你还能利用其他方法说明 b∥c 吗?
a
b
c
1
2
在同一平面内,垂直于同一条直线的两条直线平行.
大展身手:
1.如图:如果∠1=∠2,那么AB//CD,其依据可以简单说成( )
D
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
2.如图:∠1=120°,要使a//b,则∠2的大小是( )
A.60°
B.80°
C.100°
D.120°
D
3.如图:工人师傅在工程施工中,需要在同一平面内弯制一个变形
管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB//BC
B.BC//CD
C.AB // DC
D.AB与CD相交
C
4.下列画出的直线a与直线b不一定平行的是( )
C
5.如图:若 与 互补,与互补,则一定有( )
B
B.
C. D.
6.如图:若 ,则____//____;若 ,则____//____.
7.如图: 和 分别为直线 与直线
和 相交所成的角.如果 那
么当 ____时,可判定 .
第5题图
8.小明把一副三角板摆放在桌面上,如图所示,其中边
, 在同一条直线上,可以得到____//____,依据是
________________________.
内错角相等,两直线平行
AC
DE
9.如图:已知 于点 于点 .试说明: .
解: (已知),
(____________).
同理, .
(__________),
即 .
(已知),
____(__________).
____//____(________________________).
垂直的定义
等量代换
等量代换
内错角相等,两直线平行
∠4
DF
AE
10.如图,已知 平分 , 平分 ,
且 与 互余.试说明: .
解: 与 互余,
.
平分 , 平分 ,
, .
.
.
11.如图①,∠B=25°,∠D=42°,∠BCD=67°,试判断AB和DE的位置关系,并说明理由。
解:AB//DE
过点C向右作∠BCF=25°,则∠BCF=∠B,
∴AB//CF则∠DCF=∠BCD-∠BCF= 67°-25°
=42°所以________________________.
(1)请补充上述解题过程。
∴∠DCF=∠D,∴CF//ED,∴AB
(2)如图②,∠1=120°,∠2=150°,AE⊥EC,试判断AB,CD的 位置关系,并说明理由。
(2)AB//CD
如图②,过点E向右作∠AEF=60°
∵∠1=120°
∴∠1+∠AEF=180°
∴AB//EF
∵AE⊥EC,∴∠AEC=90°
∴∠FEC=90°—60°=30°
∵∠2=150°
∴∠FEC+∠2=180°
∴EF // CD
∴AB // CD
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
