人教版 九年级数学下册 27.2.1 相似三角形的判定 课件 (共23张PPT)
文档属性
| 名称 | 人教版 九年级数学下册 27.2.1 相似三角形的判定 课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 436.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 16:36:58 | ||
图片预览





文档简介
(共23张PPT)
27.2.1 相似三角形的判定
人教版 九年级 下册
教材分析
本节课通过类比相似多边形的概念,让学生尝试归纳相似三角形的概念.针对我们之前学过的全等三角形的判定方法,尝试让学生探究相似三角形的判定方法.本节课我们借助网格,通过计算得出两条直线被一组平行线所截,所得的对应线段成比例.再通过探究活动,得出平行线分线段定理推论内容.相似三角形是全等三角形的拓展,而相似三角形的判定是相似三角形的主要内容之一,它是进一步对相似三角形的本质和定义的全面研究,也是相似三角形性质的研究基础.
教学目标
教学目标:1. 理解相似三角形的概念.
2. 掌握平行线分线段成比例的基本事实及其推论.
3. 会用平行线判定两个三角形相似并进行证明和计算.
教学重点:掌握平行线分线段成比例定理的基本事实、推论以及利用平行线
法判定三角形相似.
教学难点:运用平行线分线段成比例定理的基本事实、推论以及利用平行线法
判定三角形相似来解决问题.
新知导入
情境引入
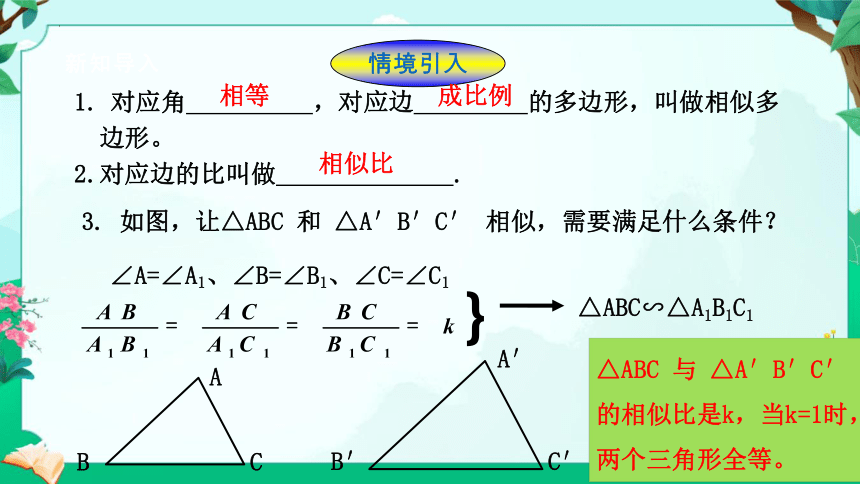
对应角 ,对应边 的多边形,叫做相似多
边形。
2.对应边的比叫做 .
3. 如图,让△ABC 和 △A′B′C′ 相似,需要满足什么条件?
相等
成比例
相似比
A
B
C
A′
B′
C′
∠A=∠A1、∠B=∠B1、∠C=∠C1
△ABC∽△A1B1C1
}
△ABC 与 △A′B′C′
的相似比是k,当k=1时,两个三角形全等。
新知讲解
合作学习
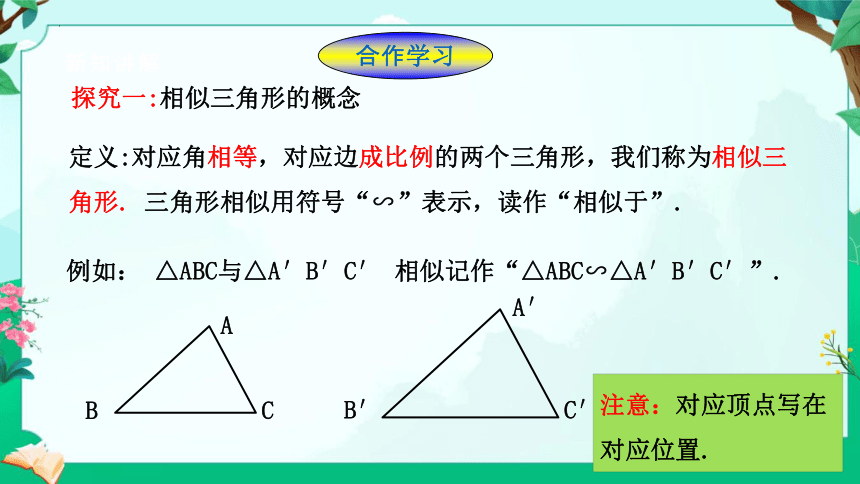
例如: △ABC与△A′B′C′ 相似记作“△ABC∽△A′B′C′”.
定义:对应角相等,对应边成比例的两个三角形,我们称为相似三角形. 三角形相似用符号“∽”表示,读作“相似于”.
注意:对应顶点写在对应位置.
探究一:相似三角形的概念
A
B
C
A′
B′
C′
如图,任意画两条直线l1,l2,再画三条与l1,l2,都相交的平行线l3,l4,l5.分别度量l3,l4,l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度.
A
C
E
B
D
F
l4
l5
l1
l2
l3
探究二:平行线分线段成比例(基本事实)
(1) 计算 的值,
它们相等吗?
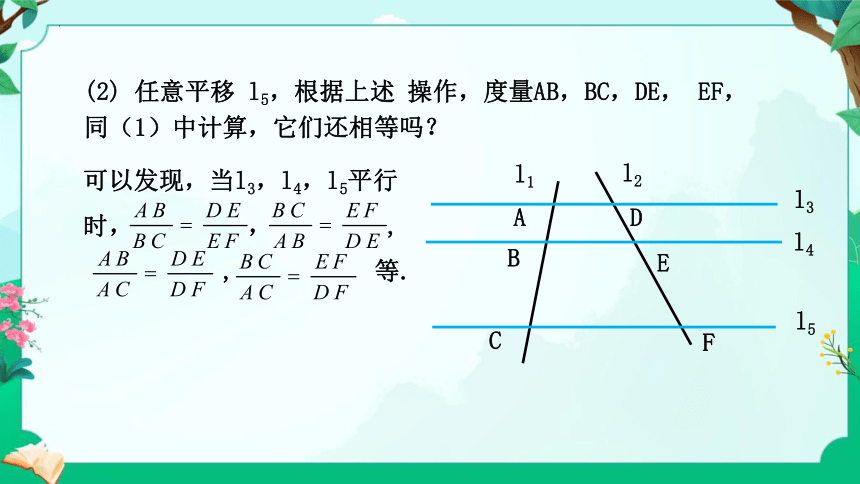
(2) 任意平移 l5,根据上述 操作,度量AB,BC,DE, EF, 同(1)中计算,它们还相等吗?
A
C
E
B
D
F
l4
l5
l1
l2
l3
可以发现,当l3,l4,l5平行时, , ,
, 等.
提炼概念
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若l3∥l4∥ l5,则
, ,
,
归纳总结:
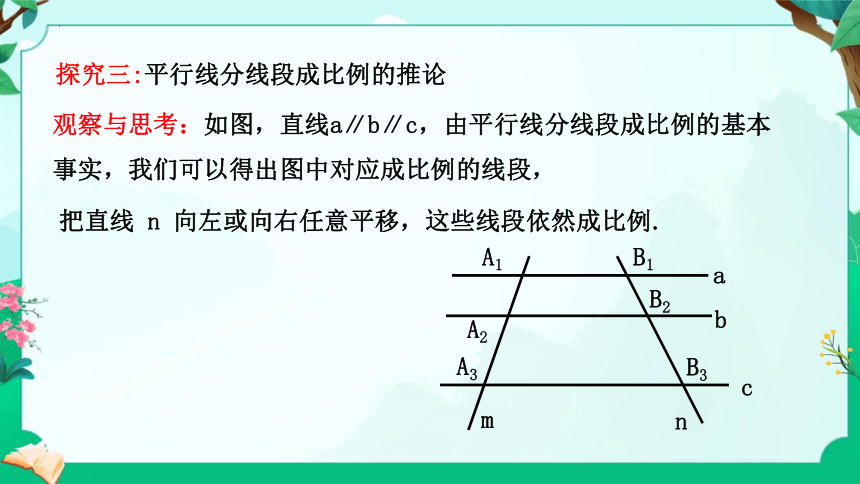
观察与思考:如图,直线a∥b∥c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
把直线 n 向左或向右任意平移,这些线段依然成比例.
A1
A2
A3
b
c
m
B1
B2
B3
n
a
探究三:平行线分线段成比例的推论
A1
A2
A3
b
c
m
B1
B2
B3
n
a
若把直线 n 向左平移到 B1 与A1 重合的位置,说说图中有哪些成比例线段?
得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
A1
A2
A3
b
c
m
B1
B2
B3
n
a
若把 直线 n 向左平移到 B2 与A2 重合的位置,说说图中有哪些成比例线段?
得到新的图形,刚刚所说的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
( )
平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例. (“A”型和“X”型)
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳总结:平行线分线段成比例的推论
符号语言:
如左图,∵A2B2∥ A3B3
探究四:三角形相似的判定定理一
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题(1) :△ADE与△ABC的三个内角分别相等吗?
问题(2) :它们的边长是否对应成比例?
B
C
A
D
E
(1) 由DE∥BC及∠A是公共角得三个内角
对应相等;
(2)由前面的结论可得 ,而 中的DE不在△ABC的边BC上,不能直接利用前面的结论.
如何证明三边长对应成比例呢?
B
C
A
D
E
要证明 ,而除 DE 外,其他的线段都在
△ABC 的边上,要想利用前面学到的结论来证明三角形相似,
需要怎样做呢?
可以将 DE 平移到BC 边上去
证明:
在 △ADE与 △ABC中,∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点 E 作 EF∥AB,交 BC 于点 F.
C
A
B
D
E
F
用相似的定义证明△ADE∽△ABC
∵ DE∥BC,EF∥AB,
∴
∵ 四边形DEFB为平行四边形,
∴ DE=BF.
∴△ADE∽△ABC.
∴
三角形相似的两种常见类型:
“A ”型
“X ”型
D
E
A
B
C
A
B
C
D
E
相似三角形的判定定理(一):
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
典例精讲
例: 如图,F是平行四边形ABCD的边CD上一点,连接BF,并延长BF交AD的延长线于点E.
求证:
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC.
(平行于三角形一边的直线截其他两边,所得的对应线段成比例).
同理可得
归纳概念
平行线除了具备造成“三线八角”相等或互补的
功能外,还可以分线段成比例,而利用平行线得线
段成比例的基本思路是:
(1)善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
(2)平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
课堂练习
1.在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
A.AB:AD =1:2 B.AE:EC=1:2
C.AD:EC=1:2 D.DE:BC=1:2
2.如图,直线l1∥l2∥l3.直线AC交l1,l2,l3于点A,B,C,直线DF交l1,l2,l3于点D,E,F,已知 , = .
B
2
4.如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB.
解:
课堂总结
说一说
1、平行线分线段成比例的基本事实是什么?
2、平行线分线段成比例的推论是什么?符合语言是什么?
3、三角形相似的判定定理一是什么?符号语言是什么?
本节课你有哪些收获?
27.2.1 相似三角形的判定
人教版 九年级 下册
教材分析
本节课通过类比相似多边形的概念,让学生尝试归纳相似三角形的概念.针对我们之前学过的全等三角形的判定方法,尝试让学生探究相似三角形的判定方法.本节课我们借助网格,通过计算得出两条直线被一组平行线所截,所得的对应线段成比例.再通过探究活动,得出平行线分线段定理推论内容.相似三角形是全等三角形的拓展,而相似三角形的判定是相似三角形的主要内容之一,它是进一步对相似三角形的本质和定义的全面研究,也是相似三角形性质的研究基础.
教学目标
教学目标:1. 理解相似三角形的概念.
2. 掌握平行线分线段成比例的基本事实及其推论.
3. 会用平行线判定两个三角形相似并进行证明和计算.
教学重点:掌握平行线分线段成比例定理的基本事实、推论以及利用平行线
法判定三角形相似.
教学难点:运用平行线分线段成比例定理的基本事实、推论以及利用平行线法
判定三角形相似来解决问题.
新知导入
情境引入
对应角 ,对应边 的多边形,叫做相似多
边形。
2.对应边的比叫做 .
3. 如图,让△ABC 和 △A′B′C′ 相似,需要满足什么条件?
相等
成比例
相似比
A
B
C
A′
B′
C′
∠A=∠A1、∠B=∠B1、∠C=∠C1
△ABC∽△A1B1C1
}
△ABC 与 △A′B′C′
的相似比是k,当k=1时,两个三角形全等。
新知讲解
合作学习
例如: △ABC与△A′B′C′ 相似记作“△ABC∽△A′B′C′”.
定义:对应角相等,对应边成比例的两个三角形,我们称为相似三角形. 三角形相似用符号“∽”表示,读作“相似于”.
注意:对应顶点写在对应位置.
探究一:相似三角形的概念
A
B
C
A′
B′
C′
如图,任意画两条直线l1,l2,再画三条与l1,l2,都相交的平行线l3,l4,l5.分别度量l3,l4,l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度.
A
C
E
B
D
F
l4
l5
l1
l2
l3
探究二:平行线分线段成比例(基本事实)
(1) 计算 的值,
它们相等吗?
(2) 任意平移 l5,根据上述 操作,度量AB,BC,DE, EF, 同(1)中计算,它们还相等吗?
A
C
E
B
D
F
l4
l5
l1
l2
l3
可以发现,当l3,l4,l5平行时, , ,
, 等.
提炼概念
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若l3∥l4∥ l5,则
, ,
,
归纳总结:
观察与思考:如图,直线a∥b∥c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
把直线 n 向左或向右任意平移,这些线段依然成比例.
A1
A2
A3
b
c
m
B1
B2
B3
n
a
探究三:平行线分线段成比例的推论
A1
A2
A3
b
c
m
B1
B2
B3
n
a
若把直线 n 向左平移到 B1 与A1 重合的位置,说说图中有哪些成比例线段?
得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
A1
A2
A3
b
c
m
B1
B2
B3
n
a
若把 直线 n 向左平移到 B2 与A2 重合的位置,说说图中有哪些成比例线段?
得到新的图形,刚刚所说的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
( )
平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例. (“A”型和“X”型)
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳总结:平行线分线段成比例的推论
符号语言:
如左图,∵A2B2∥ A3B3
探究四:三角形相似的判定定理一
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题(1) :△ADE与△ABC的三个内角分别相等吗?
问题(2) :它们的边长是否对应成比例?
B
C
A
D
E
(1) 由DE∥BC及∠A是公共角得三个内角
对应相等;
(2)由前面的结论可得 ,而 中的DE不在△ABC的边BC上,不能直接利用前面的结论.
如何证明三边长对应成比例呢?
B
C
A
D
E
要证明 ,而除 DE 外,其他的线段都在
△ABC 的边上,要想利用前面学到的结论来证明三角形相似,
需要怎样做呢?
可以将 DE 平移到BC 边上去
证明:
在 △ADE与 △ABC中,∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点 E 作 EF∥AB,交 BC 于点 F.
C
A
B
D
E
F
用相似的定义证明△ADE∽△ABC
∵ DE∥BC,EF∥AB,
∴
∵ 四边形DEFB为平行四边形,
∴ DE=BF.
∴△ADE∽△ABC.
∴
三角形相似的两种常见类型:
“A ”型
“X ”型
D
E
A
B
C
A
B
C
D
E
相似三角形的判定定理(一):
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
典例精讲
例: 如图,F是平行四边形ABCD的边CD上一点,连接BF,并延长BF交AD的延长线于点E.
求证:
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC.
(平行于三角形一边的直线截其他两边,所得的对应线段成比例).
同理可得
归纳概念
平行线除了具备造成“三线八角”相等或互补的
功能外,还可以分线段成比例,而利用平行线得线
段成比例的基本思路是:
(1)善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
(2)平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
课堂练习
1.在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
A.AB:AD =1:2 B.AE:EC=1:2
C.AD:EC=1:2 D.DE:BC=1:2
2.如图,直线l1∥l2∥l3.直线AC交l1,l2,l3于点A,B,C,直线DF交l1,l2,l3于点D,E,F,已知 , = .
B
2
4.如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB.
解:
课堂总结
说一说
1、平行线分线段成比例的基本事实是什么?
2、平行线分线段成比例的推论是什么?符合语言是什么?
3、三角形相似的判定定理一是什么?符号语言是什么?
本节课你有哪些收获?
