3.4.1 基本不等式课件
图片预览







文档简介
课件20张PPT。3.4.1 基本不等式By 郭玉莲
我们经常接触的式子大多数是等式,而在客观世界中,有些不等关系是永远成立的。
例如:
在周长相等时,圆的面积比正方形的面积
大,正方形的面积又比非正方形的任意矩形
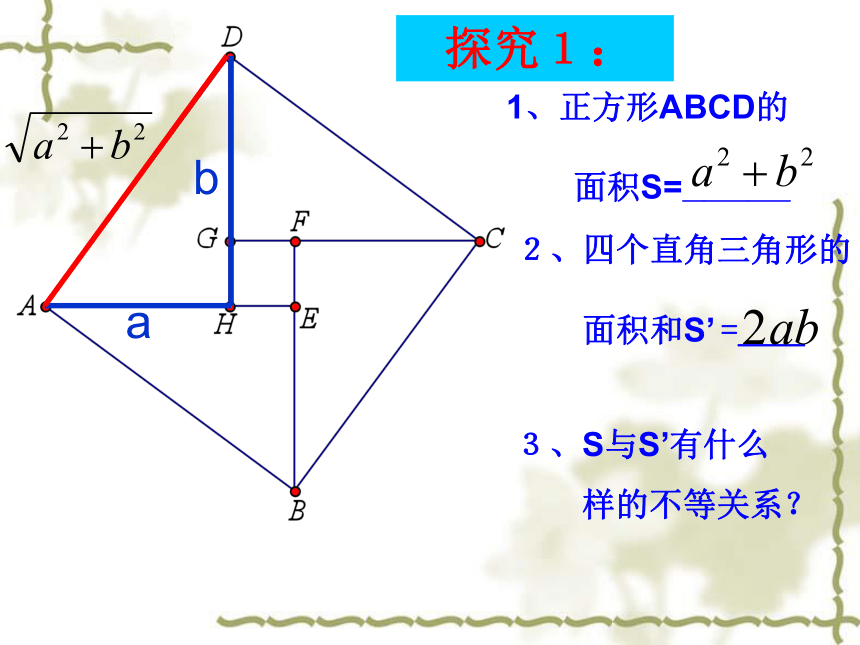
的面积大。 这是2002年在北京召开的第24届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。ab1、正方形ABCD的
面积S=_____2、四个直角三角形的
面积和S’ =__3、S与S’有什么
样的不等关系? 探究1: 若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,取“=”号)文字叙述为:两数的平方和不小于积的2倍。 结论1:证明:那么a2+b2≥2 a b那么a + b ≥2 (当且仅当a=b时,取“=”号)若a∈R,b∈R若a>0 b>0 如果a>0,b>0,我们用 去替换a、b,能得到什么结论?
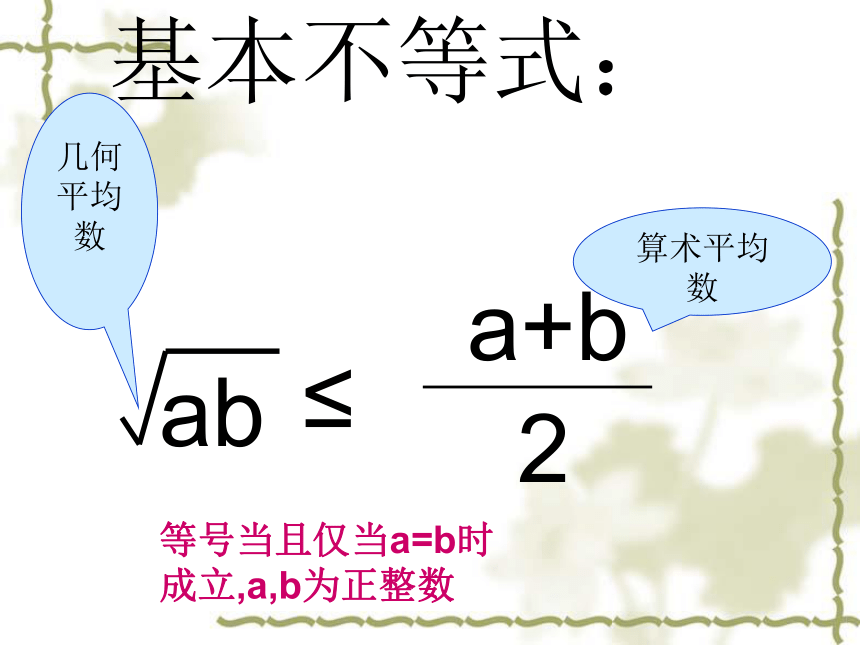
探究2:(当且仅当a=b时,取“=”号)(a>0,b>0) 结论 2:基本不等式:ab≤a+b2几何平均数算术平均数等号当且仅当a=b时成立,a,b为正整数 两个正数的算术平均数不小于它们的几何平均数 探究3:ABCDE1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____2、你能用这个图形得出基本不等式
几何解释吗?ab半弦不大于半径我们把 叫做a,b的算术平均数,把 叫做a,b的几何平均数;
文字叙述为:两个正数的算术平均数不小于它们的几何平均数,因此也叫均值不等式;
从形的角度来看,基本不等式具有特定的几何意义;从数的角度来看,基本不等式揭示了“和”与“积”这两种结构间的不等关系;
注意基本不等式成立的条件 :
⑴ a、 b是两个正数;
⑵ 当且仅当a=b时“=”号成立。剖析公式 解:<<例1.试判断 与 2 的大小 关系?
变式(1):试判断 与 2 的大小关系? 例题讲解变式(2):求 的最值等号“=”当且仅当x=1/x时成立解: 例题讲解例2: (1)用篱笆围一个面积为100 平方米的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短的篱笆是多少? (2)一段长为36 m的篱笆围成一个矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少?课堂小结1、本节课主要学习了基本不等式的证明与初步应用。2、注意公式的正向、逆向使用的条件以
及“=”成立的条件。 (1)若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,取“=”号) (2) (当且仅当a=b时,取“=”号) 3、会用基本不等式解决简单的最大(小)值问题。 巩固练习1、用20cm长的铁丝折成一个面积最大的矩形,应怎样折?
2、已知直角三角形的面积等于50,两条直角边各为多少时,两条直角边的和最小,最小值是多少?作业与思考:1、作业
课本第100页习题3.4A第1﹑2题。
2、思考题:若x>3 ,求 的最小值
我们经常接触的式子大多数是等式,而在客观世界中,有些不等关系是永远成立的。
例如:
在周长相等时,圆的面积比正方形的面积
大,正方形的面积又比非正方形的任意矩形
的面积大。 这是2002年在北京召开的第24届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。ab1、正方形ABCD的
面积S=_____2、四个直角三角形的
面积和S’ =__3、S与S’有什么
样的不等关系? 探究1: 若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,取“=”号)文字叙述为:两数的平方和不小于积的2倍。 结论1:证明:那么a2+b2≥2 a b那么a + b ≥2 (当且仅当a=b时,取“=”号)若a∈R,b∈R若a>0 b>0 如果a>0,b>0,我们用 去替换a、b,能得到什么结论?
探究2:(当且仅当a=b时,取“=”号)(a>0,b>0) 结论 2:基本不等式:ab≤a+b2几何平均数算术平均数等号当且仅当a=b时成立,a,b为正整数 两个正数的算术平均数不小于它们的几何平均数 探究3:ABCDE1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____2、你能用这个图形得出基本不等式
几何解释吗?ab半弦不大于半径我们把 叫做a,b的算术平均数,把 叫做a,b的几何平均数;
文字叙述为:两个正数的算术平均数不小于它们的几何平均数,因此也叫均值不等式;
从形的角度来看,基本不等式具有特定的几何意义;从数的角度来看,基本不等式揭示了“和”与“积”这两种结构间的不等关系;
注意基本不等式成立的条件 :
⑴ a、 b是两个正数;
⑵ 当且仅当a=b时“=”号成立。剖析公式 解:<<例1.试判断 与 2 的大小 关系?
变式(1):试判断 与 2 的大小关系? 例题讲解变式(2):求 的最值等号“=”当且仅当x=1/x时成立解: 例题讲解例2: (1)用篱笆围一个面积为100 平方米的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短的篱笆是多少? (2)一段长为36 m的篱笆围成一个矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少?课堂小结1、本节课主要学习了基本不等式的证明与初步应用。2、注意公式的正向、逆向使用的条件以
及“=”成立的条件。 (1)若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,取“=”号) (2) (当且仅当a=b时,取“=”号) 3、会用基本不等式解决简单的最大(小)值问题。 巩固练习1、用20cm长的铁丝折成一个面积最大的矩形,应怎样折?
2、已知直角三角形的面积等于50,两条直角边各为多少时,两条直角边的和最小,最小值是多少?作业与思考:1、作业
课本第100页习题3.4A第1﹑2题。
2、思考题:若x>3 ,求 的最小值
