19.2.1正比例函数导学案
文档属性
| 名称 | 19.2.1正比例函数导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 40.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-02 00:00:00 | ||
图片预览


文档简介
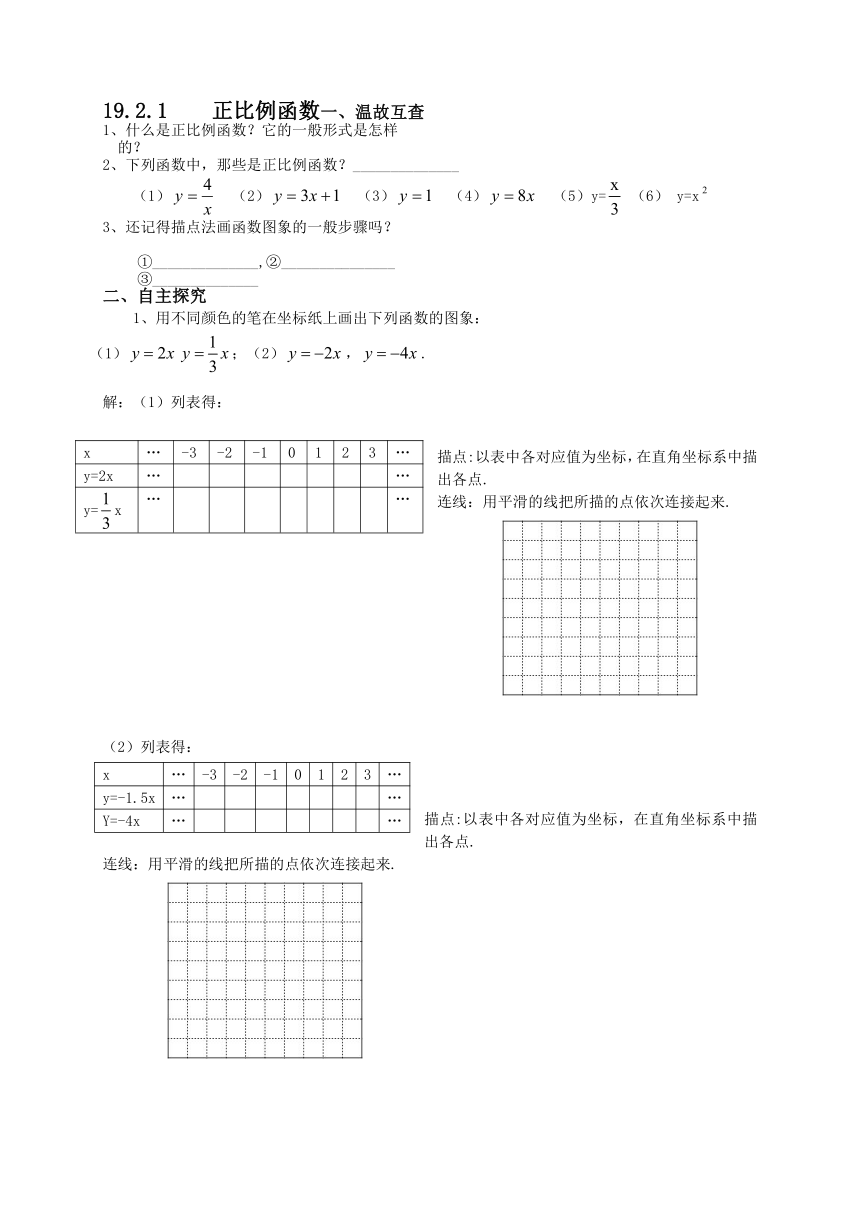
19.2.1 正比例函数一、温故互查
1、什么是正比例函数?它的一般形式是怎样
的?
2、下列函数中,那些是正比例函数?______________
(1) (2) (3) (4) (5)y= (6) y=x
3、还记得描点法画函数图象的一般步骤吗?
①______________,②_______________
③______________
二、自主探究
1、用不同颜色的笔在坐标纸上画出下列函数的图象:
(1);(2),.
解:(1)列表得:
x … -3 -2 -1 0 1 2 3 …
y=2x … …
y=x … …
描点:以表中各对应值为坐标,在直角坐标系中描出各点.
连线:用平滑的线把所描的点依次连接起来.
(2)列表得:
x … -3 -2 -1 0 1 2 3 …
y=-1.5x … …
Y=-4x … …
描点:以表中各对应值为坐标,在直角坐标系中描出各点.
连线:用平滑的线把所描的点依次连接起来.
探究:1.观察(1)中所画图像,填写你发现的规律:
函数和y= x的图像是经过原点的 __________,
函数和y= x的图像经过第
_______象限,从左到右_______,即y随x的增大而________;
归纳:正比例函数()的图像经过第_______象限,从左到右_______,即y随x的增大而________.
2、观察(2)中所画图像,填写你发现的规律:
(1)函数和y=-4x的图像是经过原点的 __________.
(2)函数和y=-4x的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
归纳:函数()的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
总结:正比例函数(k≠0)是一条经过 .
当k > 0时,直线经过 象限,从左
到右呈 趋势,即随的增大而
当k〈0时,直线经过 象限,从左
到右呈 趋势,即随的减小 而 .
3.因为过 点有且只有一条直线,我们
在画正比例函数图象时,只需确定两点,通常
是( , )和( , ).
三、尝试解题
1、用最简单的方法 在同一直角坐标系中,分别作出下列函数的图像: y=x,y=-3x.
2.一列火车以90km/h的速度匀速前进.求它的行驶路程s(单位:km)关于时间t(单位:h)的函数解析式,并画出函数图象.
3.函数y=-5x的图象在第_______象限,经过点(0,____)与点(1,_____),y随x的增大而________.
四、巩固训练
1.函数y=(k-)xk2是正比例函数,且y随x的增大而减小,则k=_______
2.函数y=kx(k≠0)的图象过P(-3,3),则k=____,图象过_____象限.
3.设函数是正比例函数,且图像过一、三象限,则m的值为 _________.
五、归纳小结
六、当堂检测
1.已知正比例函数如果的值随的值增大而减小,那么的取值范圆是 .
2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是 .
3.当时,函数的图像在第( )象限.
A、一、三 B、二、四 C、二 D、三
4. 关于函数,下列结论中正确的是 ( )
A.函数图象经过点(1,2)
B.函数图象经过第二、四象限
C.随的增大而增大
D.不论取何值,总有>0
5.正比例函数y=(3m-1)x的图像经过点A(x1,x2)和B(y1,y2),且该图像经过第二、四象限.
(1)求m的取值范围
(2)当x1>x2时,比较 y1与y2的大小,并说明理由.
1、什么是正比例函数?它的一般形式是怎样
的?
2、下列函数中,那些是正比例函数?______________
(1) (2) (3) (4) (5)y= (6) y=x
3、还记得描点法画函数图象的一般步骤吗?
①______________,②_______________
③______________
二、自主探究
1、用不同颜色的笔在坐标纸上画出下列函数的图象:
(1);(2),.
解:(1)列表得:
x … -3 -2 -1 0 1 2 3 …
y=2x … …
y=x … …
描点:以表中各对应值为坐标,在直角坐标系中描出各点.
连线:用平滑的线把所描的点依次连接起来.
(2)列表得:
x … -3 -2 -1 0 1 2 3 …
y=-1.5x … …
Y=-4x … …
描点:以表中各对应值为坐标,在直角坐标系中描出各点.
连线:用平滑的线把所描的点依次连接起来.
探究:1.观察(1)中所画图像,填写你发现的规律:
函数和y= x的图像是经过原点的 __________,
函数和y= x的图像经过第
_______象限,从左到右_______,即y随x的增大而________;
归纳:正比例函数()的图像经过第_______象限,从左到右_______,即y随x的增大而________.
2、观察(2)中所画图像,填写你发现的规律:
(1)函数和y=-4x的图像是经过原点的 __________.
(2)函数和y=-4x的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
归纳:函数()的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
总结:正比例函数(k≠0)是一条经过 .
当k > 0时,直线经过 象限,从左
到右呈 趋势,即随的增大而
当k〈0时,直线经过 象限,从左
到右呈 趋势,即随的减小 而 .
3.因为过 点有且只有一条直线,我们
在画正比例函数图象时,只需确定两点,通常
是( , )和( , ).
三、尝试解题
1、用最简单的方法 在同一直角坐标系中,分别作出下列函数的图像: y=x,y=-3x.
2.一列火车以90km/h的速度匀速前进.求它的行驶路程s(单位:km)关于时间t(单位:h)的函数解析式,并画出函数图象.
3.函数y=-5x的图象在第_______象限,经过点(0,____)与点(1,_____),y随x的增大而________.
四、巩固训练
1.函数y=(k-)xk2是正比例函数,且y随x的增大而减小,则k=_______
2.函数y=kx(k≠0)的图象过P(-3,3),则k=____,图象过_____象限.
3.设函数是正比例函数,且图像过一、三象限,则m的值为 _________.
五、归纳小结
六、当堂检测
1.已知正比例函数如果的值随的值增大而减小,那么的取值范圆是 .
2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是 .
3.当时,函数的图像在第( )象限.
A、一、三 B、二、四 C、二 D、三
4. 关于函数,下列结论中正确的是 ( )
A.函数图象经过点(1,2)
B.函数图象经过第二、四象限
C.随的增大而增大
D.不论取何值,总有>0
5.正比例函数y=(3m-1)x的图像经过点A(x1,x2)和B(y1,y2),且该图像经过第二、四象限.
(1)求m的取值范围
(2)当x1>x2时,比较 y1与y2的大小,并说明理由.
