新人教版19.2.1正比例函数导学案
文档属性
| 名称 | 新人教版19.2.1正比例函数导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-02 00:00:00 | ||
图片预览

文档简介
19.2.1 正比例函数
学习目标:
1、理解正比例函数的概念,在用描点法画正比例函数图象过程中发现正比例函数图象性质
2、能用正比例函数图象的性质简便地画出正比例函数图像
3、能够利用正比例函数解决简单的数学问题
学习重点:画正比例函数图像及总结正比例函数的性质
学习难点:正比例函数图像的性质
思维导航:正比例函数中对比例系数K是常数且K=0
结合图像归纳出正比例函数的增减性
学习过程:
(一) 、正比例函数的概念
1.下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式。这些函数解析式有哪些共同特征?
(1)圆的周长随半径的变化而变化。
(2)铁的密度为7.8g/,铁块的质量m(单位:g)随它的体积V(单位:)的变化而变化。
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h(单位:cm)随练习本的本数n的变化而变化。
(4)冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:min)的变化而变化。
2.观察“思考”所得的四个函数;
(1)观察这些函数关系式,这些函数都是常数与自变量 的形式;
(2)一般地,形如 ( )函数,叫做正比例函数,其中叫做 。
跟踪练习(一):
1、下列函数中,那些是正比例函数?______________
(1) (2) (3) (4) (5)y= (6) y=x
2.已知一个正比例函数的比例系数是-5,则它的解析式为____________
3.关于x的函数是正比例函数,则m__________
4.若y=5x是正比例函数,则m=___________.
5. 若是正比例函数,则= .
(二)正比例函数图像的画法与性质
知识链接:用描点法画函数图象的一般步骤:
①______________,②___________________③___________________
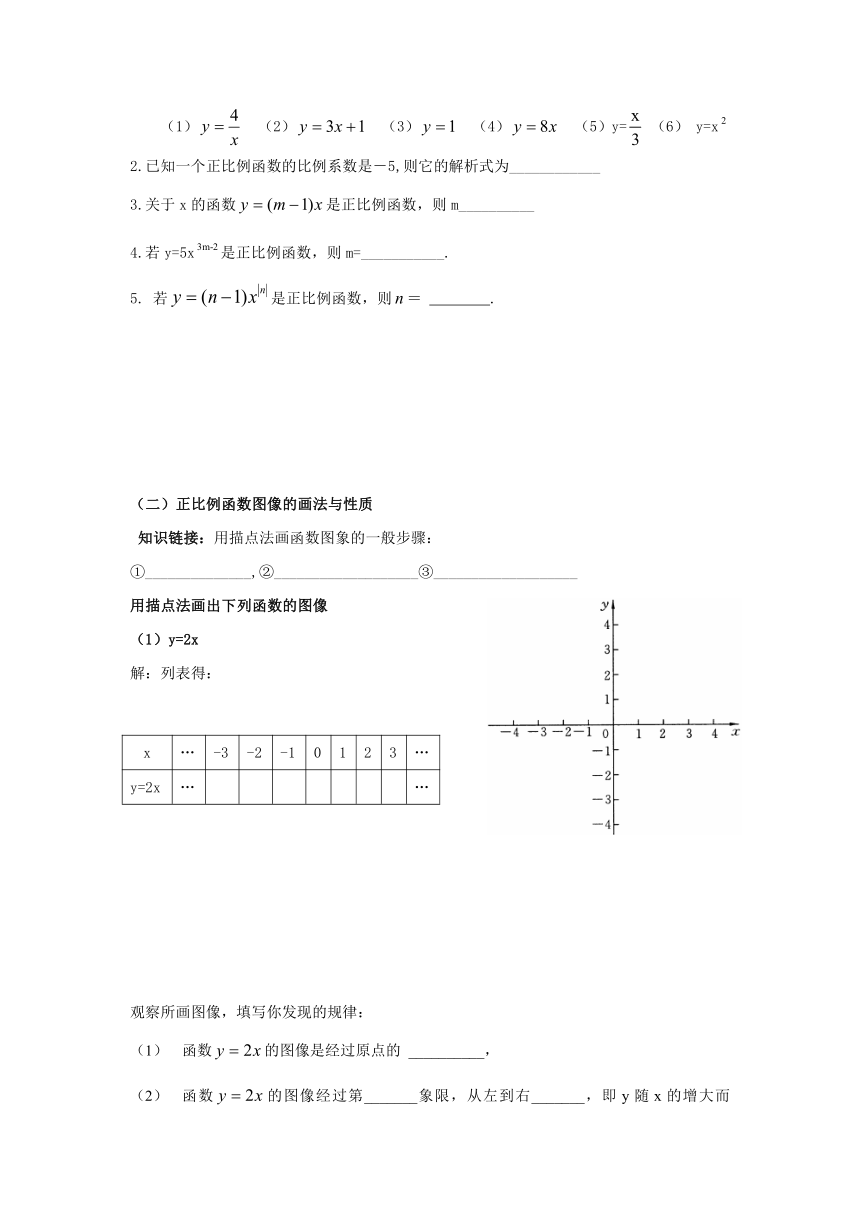
用描点法画出下列函数的图像
(1)y=2x
解:列表得:
x … -3 -2 -1 0 1 2 3 …
y=2x … …
观察所画图像,填写你发现的规律:
函数的图像是经过原点的 __________,
函数的图像经过第_______象限,从左到右_______,即y随x的增大而________;
函数()的图像经过第_______象限,从左到右_______,即y随x的增大而________;
(2) y=-2x
解:列表得:
x … …
y=-2 … …
观察所画图像,填写你发现的规律:
函数的图像是经过原点的 __________.
函数的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
函数()的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
总结:正比例函数的性质
正比例函数(k≠0)是一条经过 .
当k > 0时,直线经过 象限,从左到右呈 趋势,即随的增大而
当k〈0时,直线经过 象限,从左到右呈 趋势,即随的减小 而
跟踪练习(二):
1.已知正比例函数,若随的增大而增大,则的取值范围是( ) A.k<0 B.k>0 C. D.
2.已知正比例函数的图像过第二、四象限,则( )
A、y随x的增大而增大 B、y随x的增大而减小
C、当时,y随x的增大而增大;当时,y随x的增大而减少;
D、不论x如何变化,y不变。
3.当时,函数的图像在第( )象限。
A、一、三 B、二、四 C、二 D、三
4.函数的图像在第_______象限,经过点(0,____)与点(1,____),y随x的增大而_________
(三)两点法画正比例函数的图像
1.因为 点确定一条直线,我们在画正比例函数图象时,只需确定两点即可,通常是( , )和( , )
2.试一试:用最简单的方法画出下列函数的图像
(1)、 y=-3x (2) y=x
(四)达标测评
1.y=, y=, y=3x+9, y=2x中,正比例函数是____________.
2.若x、y是变量,且函数y=(k+1)是正比例函数,则k=_________.
3.若函数是关于的正比例函数,则
4.函数的图像经过点P(-1,3)则k的值为( )
A、3 B、—3 C、 D、
5.正比例函数y=kx(k为常数,k<0)的图象依次经过第________象限,函数值随自变量的增大而_________.
6.函数y=kx(k≠0)的图象过P(-3,3),则k=____,图象过_____象限。
7.设函数是正比例函数,且图像过一、三象限,则m的值为 。
8. 在函数y=2x的自变量中任意取两个点x,x,若x<x,则对应的函数值y与y的大小关系是y___y.
9.已知y与x成正比例,且x=2时y=-6,则y=9时x的值
10.已知点A(-2,3),B(5,m)在正比例函数的图象上,求m的值。
学习目标:
1、理解正比例函数的概念,在用描点法画正比例函数图象过程中发现正比例函数图象性质
2、能用正比例函数图象的性质简便地画出正比例函数图像
3、能够利用正比例函数解决简单的数学问题
学习重点:画正比例函数图像及总结正比例函数的性质
学习难点:正比例函数图像的性质
思维导航:正比例函数中对比例系数K是常数且K=0
结合图像归纳出正比例函数的增减性
学习过程:
(一) 、正比例函数的概念
1.下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式。这些函数解析式有哪些共同特征?
(1)圆的周长随半径的变化而变化。
(2)铁的密度为7.8g/,铁块的质量m(单位:g)随它的体积V(单位:)的变化而变化。
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h(单位:cm)随练习本的本数n的变化而变化。
(4)冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:min)的变化而变化。
2.观察“思考”所得的四个函数;
(1)观察这些函数关系式,这些函数都是常数与自变量 的形式;
(2)一般地,形如 ( )函数,叫做正比例函数,其中叫做 。
跟踪练习(一):
1、下列函数中,那些是正比例函数?______________
(1) (2) (3) (4) (5)y= (6) y=x
2.已知一个正比例函数的比例系数是-5,则它的解析式为____________
3.关于x的函数是正比例函数,则m__________
4.若y=5x是正比例函数,则m=___________.
5. 若是正比例函数,则= .
(二)正比例函数图像的画法与性质
知识链接:用描点法画函数图象的一般步骤:
①______________,②___________________③___________________
用描点法画出下列函数的图像
(1)y=2x
解:列表得:
x … -3 -2 -1 0 1 2 3 …
y=2x … …
观察所画图像,填写你发现的规律:
函数的图像是经过原点的 __________,
函数的图像经过第_______象限,从左到右_______,即y随x的增大而________;
函数()的图像经过第_______象限,从左到右_______,即y随x的增大而________;
(2) y=-2x
解:列表得:
x … …
y=-2 … …
观察所画图像,填写你发现的规律:
函数的图像是经过原点的 __________.
函数的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
函数()的图像经过第_______象限,从左到右呈_______趋势,即y随x的增大而________;
总结:正比例函数的性质
正比例函数(k≠0)是一条经过 .
当k > 0时,直线经过 象限,从左到右呈 趋势,即随的增大而
当k〈0时,直线经过 象限,从左到右呈 趋势,即随的减小 而
跟踪练习(二):
1.已知正比例函数,若随的增大而增大,则的取值范围是( ) A.k<0 B.k>0 C. D.
2.已知正比例函数的图像过第二、四象限,则( )
A、y随x的增大而增大 B、y随x的增大而减小
C、当时,y随x的增大而增大;当时,y随x的增大而减少;
D、不论x如何变化,y不变。
3.当时,函数的图像在第( )象限。
A、一、三 B、二、四 C、二 D、三
4.函数的图像在第_______象限,经过点(0,____)与点(1,____),y随x的增大而_________
(三)两点法画正比例函数的图像
1.因为 点确定一条直线,我们在画正比例函数图象时,只需确定两点即可,通常是( , )和( , )
2.试一试:用最简单的方法画出下列函数的图像
(1)、 y=-3x (2) y=x
(四)达标测评
1.y=, y=, y=3x+9, y=2x中,正比例函数是____________.
2.若x、y是变量,且函数y=(k+1)是正比例函数,则k=_________.
3.若函数是关于的正比例函数,则
4.函数的图像经过点P(-1,3)则k的值为( )
A、3 B、—3 C、 D、
5.正比例函数y=kx(k为常数,k<0)的图象依次经过第________象限,函数值随自变量的增大而_________.
6.函数y=kx(k≠0)的图象过P(-3,3),则k=____,图象过_____象限。
7.设函数是正比例函数,且图像过一、三象限,则m的值为 。
8. 在函数y=2x的自变量中任意取两个点x,x,若x<x,则对应的函数值y与y的大小关系是y___y.
9.已知y与x成正比例,且x=2时y=-6,则y=9时x的值
10.已知点A(-2,3),B(5,m)在正比例函数的图象上,求m的值。
