19.2.3一次函数与方程、不等式习题
文档属性
| 名称 | 19.2.3一次函数与方程、不等式习题 |

|
|
| 格式 | zip | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-02 15:50:21 | ||
图片预览


文档简介
19.2.3一次函数与方程、不等式 习题
一、选择题
1.如图所示,点A(2,a),B(3,b)在y=x-1的图象上,则( )
( http: / / www.21cnjy.com )
A.a>b
B.aC.a=b
D.无法确定
2.如图所示,已知,下列说法不正确的是( )
( http: / / www.21cnjy.com )
A.当x>4时,
B.当x=4时,
C.当x<0时,
D.当x<4时,
3.直线与直线y=-2x+3一定相交,且交点坐标为( )
A.(4,0)
B.(-2,7)
C.(2,-1)
D.(0,-2)
4.一次函数和的图象与y轴交点的纵坐标互为相反数,则m的值为( )
A.-4
B.-3
C.2
D.-2
5.如果点(1,2)是直线:y=ax+b与直线的交点,当x<1时,则( )
A.在的上方
B. 在的下方
C.A、B都有可能
D.无法判断
6.已知点M(4,3)和点N(1,-2),点P在x轴上,当PM+PN最短时,点P的坐标是
A.(1,0))
B.(2,0)
C.(3,0)
D.(,0)
二、填空题
7.如图所示为某一次函数的图象,由图可知:y>0时,x______;x<0时,y_____.
( http: / / www.21cnjy.com )
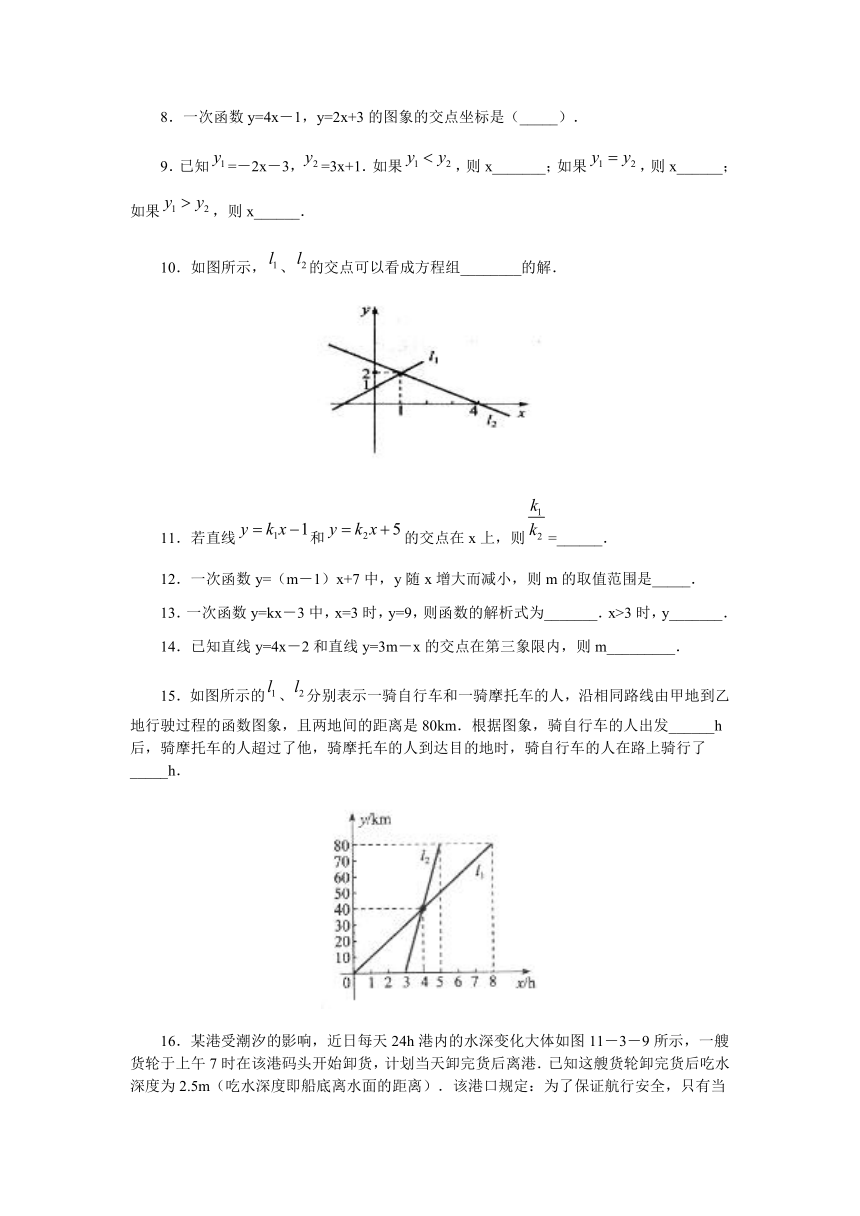
8.一次函数y=4x-1,y=2x+3的图象的交点坐标是(_____).
9.已知=-2x-3,=3x+1.如果,则x_______;如果,则x______;如果,则x______.
10.如图所示,、的交点可以看成方程组________的解.
( http: / / www.21cnjy.com )
11.若直线和的交点在x上,则=______.
12.一次函数y=(m-1)x+7中,y随x增大而减小,则m的取值范围是_____.
13.一次函数y=kx-3中,x=3时,y=9,则函数的解析式为_______.x>3时,y_______.
14.已知直线y=4x-2和直线y=3m-x的交点在第三象限内,则m_________.
15.如图所示的、分别表示一骑自行车和一骑摩托车的人,沿相同路线由甲地到乙地行驶过程的函数图象,且两地间的距离是80km.根据图象,骑自行车的人出发______h后,骑摩托车的人超过了他,骑摩托车的人到达目的地时,骑自行车的人在路上骑行了_____h.
( http: / / www.21cnjy.com )
16.某港受潮汐的影响,近日每天24h港 ( http: / / www.21cnjy.com )内的水深变化大体如图11-3-9所示,一艘货轮于上午7时在该港码头开始卸货,计划当天卸完货后离港.已知这艘货轮卸完货后吃水深度为2.5m(吃水深度即船底离水面的距离).该港口规定:为了保证航行安全,只有当船底与港内水底间的距离不小于3.5m时,才可进出该港.
( http: / / www.21cnjy.com )
根据题目中所给条件,回答下列问题.(1)要 ( http: / / www.21cnjy.com )使该货轮能在当天卸完货并安全出港,则出港时水深不能少于_______m,卸货最多只能用_______h.
(2)已知该货轮装有1200t货,先由甲装 ( http: / / www.21cnjy.com )卸队单独卸,每小时卸180t.工作了一段时间后,交由乙队接着单独卸,每小时卸120t.如果要保证货轮能在当天卸完货并安全出港,则甲队至少应工作________h.才能交给乙队接着卸货.
三、解答题
17.(1)分别画出下面每组中两个函数的图象.
①y=x+1与y=x-1.
②y=x+1与y=2x-1.
(2)上面每组中两个函数图象中有什么关系?你能再举几例吗?
(3)认真分析各组中系数之间的关系,你发现了什么?请写出来.
18.画出函数y=2x-6的图象,根据图象回答下列问题:
(1)求当x=-1时y的值.
(2)当y=-1时x的值.
(3)求方程2x-6=0的解
(4)求2x-6>0的解集.
(5)当0时x的范围.
(6)当时y的范围.
(7)如果y满足,求x的范围.
19.某电力公司为了鼓励居 ( http: / / www.21cnjy.com )民用电,采用分段计费的方法计算电费:每月用电不超过100度时,按每度0.57元计费;每月用电超过100度时,其中的100度仍按原标准收费,超过的部分按每度0.50元计费.
(1)设月用电x(度)时,应交电费y(元),求出y关于x的函数关系式.
(2)小王家第一季度交纳电费情况如下表.
月份 1月份 2月份 3月份4 合计
交费金额 76元 63元 45元6角 184元6角
问:小王家共用电多少度?
20.学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价为6000元,并且多买都有一定的优惠.
甲商场的优惠条件是:第一台按原报价收费,其余每台优惠25%.
乙商场的优惠条件是:每台优惠20%.
请你根据学校购买电脑的不同台数算一算到哪家商场买更优惠
答案
1.B
2.C
3.C
4.A
5.A
6.D
7. <1 <2
8.(2,7)
9.>- =- <-
10.
11.-
12.m<1
13.y=4x-3 y>9
14.m<-
15.4 5
16.(1)6 8
(2)4
17.(1)图象略
(2)①中两图象平行.
②中两图象相交.都能举很多例.
(3)对于直线y=x+与直线y=,=且时,两直线平行;当时,两直线相交.
18.图象略
(1)y=-8
(2)x=
(3)x=3
(4)x>3
(5)x3
(6)-4y6
(7)1x5
19.(1)y=
(2)330度
20.购买电脑不足5台时,买乙商场;超过5台时,买甲商场;刚好5台时,两商场一样.
【解题点拨】
5.把点(1,2)分别代入两直线表达式,可求得a=-3,b=5.两直线分别为y=-3x+5和y=.画出图象即可判断.
6.连结MN交x轴于P,则P满足条件.求出直线MN的表达式.令y=0,可求P点.
11.令y=0,分别由及得x=及x=-.
14.解方程组
得
两直线交点在第三象限,
16.(2)设甲队至少要工作x(h),则有180x+120(8-x)1200,解得x4.
18.(6)图象上x=1,x=6所对应的点分别为(1,-4)和(6,6),-4y6
(7)图象上y=-4和y=4所对应的点分别为(1,-4)和(5,4),1x5
19.(2)显然小王家1、2月份的电缆同超过了57元.所以,选用y=57+0.50(x-100).当y分别取76和63时,得相应的x分别为138和112.把y=45.6代入y=0.57x,可得x=80.小王家共用电138+112+80=330度.
20.设学校买电脑x(台),对甲商家付费(元),对乙商家付费(元).则=6000+(1-25%)6000(x-1),即=4500x+1500;=(1-20%)6000x即=4800x.当>时,4500x+1500>4800x.x<5.同法,=时,x=5;<时,x>5.
一、选择题
1.如图所示,点A(2,a),B(3,b)在y=x-1的图象上,则( )
( http: / / www.21cnjy.com )
A.a>b
B.a
D.无法确定
2.如图所示,已知,下列说法不正确的是( )
( http: / / www.21cnjy.com )
A.当x>4时,
B.当x=4时,
C.当x<0时,
D.当x<4时,
3.直线与直线y=-2x+3一定相交,且交点坐标为( )
A.(4,0)
B.(-2,7)
C.(2,-1)
D.(0,-2)
4.一次函数和的图象与y轴交点的纵坐标互为相反数,则m的值为( )
A.-4
B.-3
C.2
D.-2
5.如果点(1,2)是直线:y=ax+b与直线的交点,当x<1时,则( )
A.在的上方
B. 在的下方
C.A、B都有可能
D.无法判断
6.已知点M(4,3)和点N(1,-2),点P在x轴上,当PM+PN最短时,点P的坐标是
A.(1,0))
B.(2,0)
C.(3,0)
D.(,0)
二、填空题
7.如图所示为某一次函数的图象,由图可知:y>0时,x______;x<0时,y_____.
( http: / / www.21cnjy.com )
8.一次函数y=4x-1,y=2x+3的图象的交点坐标是(_____).
9.已知=-2x-3,=3x+1.如果,则x_______;如果,则x______;如果,则x______.
10.如图所示,、的交点可以看成方程组________的解.
( http: / / www.21cnjy.com )
11.若直线和的交点在x上,则=______.
12.一次函数y=(m-1)x+7中,y随x增大而减小,则m的取值范围是_____.
13.一次函数y=kx-3中,x=3时,y=9,则函数的解析式为_______.x>3时,y_______.
14.已知直线y=4x-2和直线y=3m-x的交点在第三象限内,则m_________.
15.如图所示的、分别表示一骑自行车和一骑摩托车的人,沿相同路线由甲地到乙地行驶过程的函数图象,且两地间的距离是80km.根据图象,骑自行车的人出发______h后,骑摩托车的人超过了他,骑摩托车的人到达目的地时,骑自行车的人在路上骑行了_____h.
( http: / / www.21cnjy.com )
16.某港受潮汐的影响,近日每天24h港 ( http: / / www.21cnjy.com )内的水深变化大体如图11-3-9所示,一艘货轮于上午7时在该港码头开始卸货,计划当天卸完货后离港.已知这艘货轮卸完货后吃水深度为2.5m(吃水深度即船底离水面的距离).该港口规定:为了保证航行安全,只有当船底与港内水底间的距离不小于3.5m时,才可进出该港.
( http: / / www.21cnjy.com )
根据题目中所给条件,回答下列问题.(1)要 ( http: / / www.21cnjy.com )使该货轮能在当天卸完货并安全出港,则出港时水深不能少于_______m,卸货最多只能用_______h.
(2)已知该货轮装有1200t货,先由甲装 ( http: / / www.21cnjy.com )卸队单独卸,每小时卸180t.工作了一段时间后,交由乙队接着单独卸,每小时卸120t.如果要保证货轮能在当天卸完货并安全出港,则甲队至少应工作________h.才能交给乙队接着卸货.
三、解答题
17.(1)分别画出下面每组中两个函数的图象.
①y=x+1与y=x-1.
②y=x+1与y=2x-1.
(2)上面每组中两个函数图象中有什么关系?你能再举几例吗?
(3)认真分析各组中系数之间的关系,你发现了什么?请写出来.
18.画出函数y=2x-6的图象,根据图象回答下列问题:
(1)求当x=-1时y的值.
(2)当y=-1时x的值.
(3)求方程2x-6=0的解
(4)求2x-6>0的解集.
(5)当0时x的范围.
(6)当时y的范围.
(7)如果y满足,求x的范围.
19.某电力公司为了鼓励居 ( http: / / www.21cnjy.com )民用电,采用分段计费的方法计算电费:每月用电不超过100度时,按每度0.57元计费;每月用电超过100度时,其中的100度仍按原标准收费,超过的部分按每度0.50元计费.
(1)设月用电x(度)时,应交电费y(元),求出y关于x的函数关系式.
(2)小王家第一季度交纳电费情况如下表.
月份 1月份 2月份 3月份4 合计
交费金额 76元 63元 45元6角 184元6角
问:小王家共用电多少度?
20.学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价为6000元,并且多买都有一定的优惠.
甲商场的优惠条件是:第一台按原报价收费,其余每台优惠25%.
乙商场的优惠条件是:每台优惠20%.
请你根据学校购买电脑的不同台数算一算到哪家商场买更优惠
答案
1.B
2.C
3.C
4.A
5.A
6.D
7. <1 <2
8.(2,7)
9.>- =- <-
10.
11.-
12.m<1
13.y=4x-3 y>9
14.m<-
15.4 5
16.(1)6 8
(2)4
17.(1)图象略
(2)①中两图象平行.
②中两图象相交.都能举很多例.
(3)对于直线y=x+与直线y=,=且时,两直线平行;当时,两直线相交.
18.图象略
(1)y=-8
(2)x=
(3)x=3
(4)x>3
(5)x3
(6)-4y6
(7)1x5
19.(1)y=
(2)330度
20.购买电脑不足5台时,买乙商场;超过5台时,买甲商场;刚好5台时,两商场一样.
【解题点拨】
5.把点(1,2)分别代入两直线表达式,可求得a=-3,b=5.两直线分别为y=-3x+5和y=.画出图象即可判断.
6.连结MN交x轴于P,则P满足条件.求出直线MN的表达式.令y=0,可求P点.
11.令y=0,分别由及得x=及x=-.
14.解方程组
得
两直线交点在第三象限,
16.(2)设甲队至少要工作x(h),则有180x+120(8-x)1200,解得x4.
18.(6)图象上x=1,x=6所对应的点分别为(1,-4)和(6,6),-4y6
(7)图象上y=-4和y=4所对应的点分别为(1,-4)和(5,4),1x5
19.(2)显然小王家1、2月份的电缆同超过了57元.所以,选用y=57+0.50(x-100).当y分别取76和63时,得相应的x分别为138和112.把y=45.6代入y=0.57x,可得x=80.小王家共用电138+112+80=330度.
20.设学校买电脑x(台),对甲商家付费(元),对乙商家付费(元).则=6000+(1-25%)6000(x-1),即=4500x+1500;=(1-20%)6000x即=4800x.当>时,4500x+1500>4800x.x<5.同法,=时,x=5;<时,x>5.
