23.2.3关于原点对称的点的坐标练习题1
文档属性
| 名称 | 23.2.3关于原点对称的点的坐标练习题1 |

|
|
| 格式 | zip | ||
| 文件大小 | 208.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-02 00:00:00 | ||
图片预览



文档简介
23.2.3 关于原点对称的点的坐标 练习题1
一、填空题
1.填空:两个点关于原点对称时,它们坐标符号__________,即P(x,y)关于原点的对称点为____________.
2.点P(5,-6)关于y轴对称的点的坐标是____________.
3.已知点P1(a,3)与P2(5,-3)关于原点对称,则a=______________.
4.已知点A1(4,3)与A2(-4,y)关于原点对称,则y=______________.
5.已知点M(-,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
6.已知点A(2m,-3)与B(6,1-n)关于原点对称,求出m和n的值.
7.在平面直角坐标系中,点A(5,-2)与点B(2,2)的距离是____________.
8.如果点P(x,y)关于原点的对称点为(-2,3),则x+y=____________.
9.已知点P(m-1,2)与点Q(1,2)关于y轴对称,那么m=______________.
二、选择题
10.下列说法正确的是 ( )
A.点P(4,-4)关于原点的对称点为P′(-4,-4)
B.点P(4,-4)关于原点的对称点为P′(4,-4)
C.点P(4,-4)关于原点的对称点为P′(-4,4)
D.点P(4,-4)关于原点的对称点为P′(4,4)
三.解答题
11.写出下列已知点关于原点O的对称点的坐标.
A(-2,3),B(5,-5),C(-3,-7),D(3,-2),E(4,6).
12.下列各点中哪两个点关于原点O对称?
A(3,-4),B(-4,5),C(6,-3),D(3,4),E(4,-5),F(-6,3),G(-3,4).
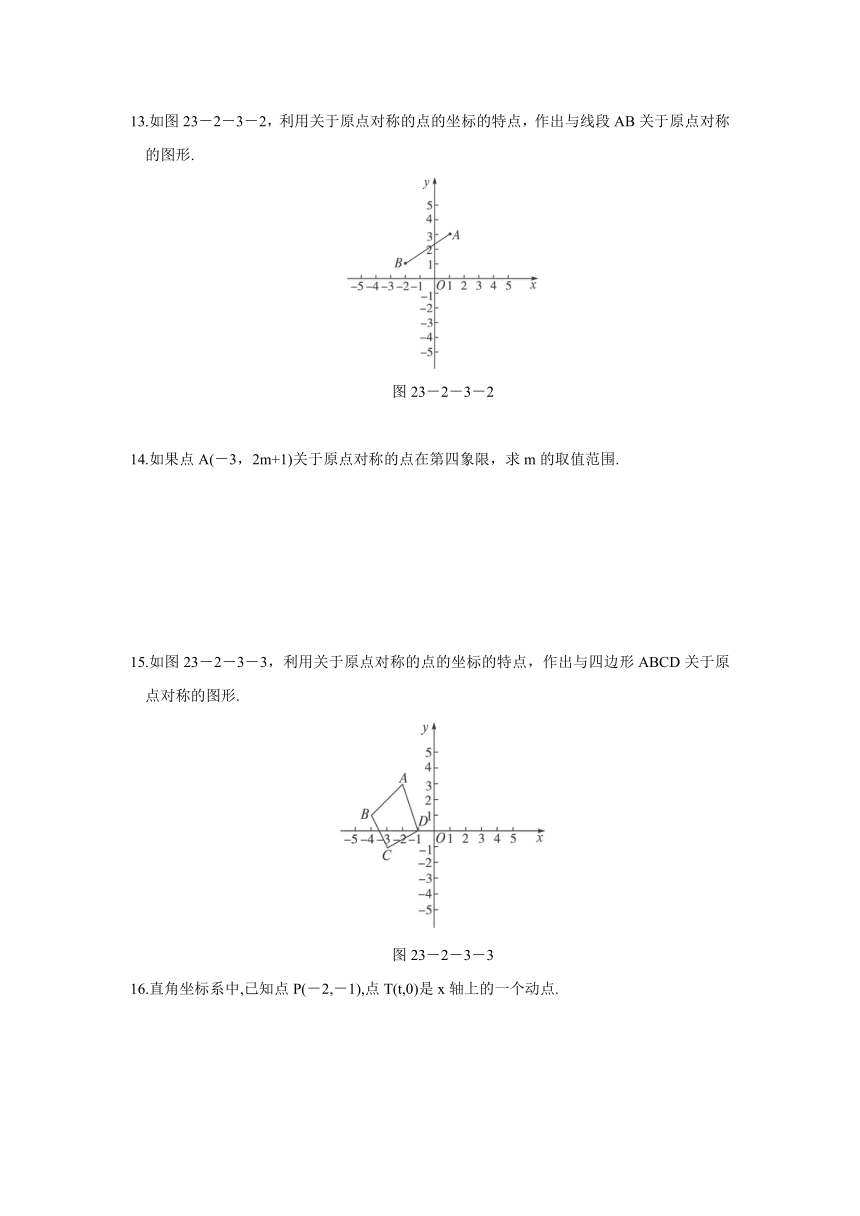
13.如图23-2-3-2,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-2
14.如果点A(-3,2m+1)关于原点对称的点在第四象限,求m的取值范围.
15.如图23-2-3-3,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-3
16.直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.
( http: / / www.21cnjy.com )
图23-2-3-4
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形
17.如图23-2-3-1,利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-1
一、课前预习 (5分钟训练)
1.填空:两个点关于原点对称时,它们坐标符号___________,即P(x,y)关于原点的对称点为____________.
思路解析:根据归纳:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y).
答案:相反 P′(-x,-y)
2.写出下列已知点关于原点O的对称点的坐标.
A(3,0),B(0,-2),C(-1,4),D(-3,-2),E(2,3).
答案:A(3,0)关于原点的对称点为A′(-3,0);B(0,-2)关于原点的对称点为B′(0,2);C(-1,4)关于原点的对称点为C′(1,-4);D(-3,-2)关于原点的对称点为D′(3,2);E(2,3)关于原点的对称点为E′(-2,-3).
3.已知点P(m-1,2)与点Q(1,2)关于y轴对称,那么m=______________.
思路解析:两点关于y轴对称,纵坐标不变,横坐标互为相反数,即m-1+1=0,∴m=0.
答案:0
4.如图23-2-3-1,利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-1
思路分析:利用关于原点对称的点的坐标的特点,先找到三角形各顶点的对应点,再首尾相连即可.
作法:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y).因此△ABC的三个顶点A(-2,2)、B(-4,-1)、C(1,1)关于原点的对称点分别为A′(2,-2)、B′(4,1)、C′(-1,-1),依次连接A′B′、B′C′、A′C′,就可得到与△ABC关于原点对称的△A′B′C′.
( http: / / www.21cnjy.com )
二、课中强化(10分钟训练)
1.写出下列已知点关于原点O的对称点的坐标.
A(-2,3),B(5,-5),C(-3,-7),D(3,-2),E(4,6).
答案:A(-2,3)关于原点的对称点为A ( http: / / www.21cnjy.com )′(2,-3);B(5,-5)关于原点的对称点为B′(-5,5);C(-3,-7)关于原点的对称点为C′(3,7);D(3,-2)关于原点的对称点为D′(-3,2);E(4,6)关于原点的对称点为E′(-4,-6).
2.下列各点中哪两个点关于原点O对称?
A(3,-4),B(-4,5),C(6,-3),D(3,4),E(4,-5),F(-6,3),G(-3,4).
答案:A(3,-4)与G(-3,4);B(-4,5)与E(4,-5);C(6,-3)与F(-6,3).
3.点P(5,-6)关于y轴对称的点的坐标是____________.
思路分析:由点坐标的几何意义可得(-5,-6).
答案:(-5,-6)
4.已知点P1(a,3)与P2(5,-3)关于原点对称,则a=______________.
答案:-5
5.如图23-2-3-2,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-2
思路分析:先找到线段两个端点的对应点,再连结即可.
作法:两个点关于原点对称时,它们坐标符号相 ( http: / / www.21cnjy.com )反,即P(x,y)关于原点的对称点为P′(-x,-y).因此AB的两个端点A(1,3)、B(-2,1)关于原点的对称点分别为A′(-1,-3)、B′(2,-1),连结A′B′,就可得到与AB关于原点对称的A′B′.
( http: / / www.21cnjy.com )
三、课后巩固(30分钟训练)
1.下列说法正确的是 ( )
A.点P(4,-4)关于原点的对称点为P′(-4,-4)
B.点P(4,-4)关于原点的对称点为P′(4,-4)
C.点P(4,-4)关于原点的对称点为P′(-4,4)
D.点P(4,-4)关于原点的对称点为P′(4,4)
答案:C
2.已知点A1(4,3)与A2(-4,y)关于原点对称,则y=______________.
答案:-3
3.已知点M(-,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
思路解析:这道题考查对称点的特点,关于原点 ( http: / / www.21cnjy.com )对称的点,它们的横纵坐标互为相反数,与点M关于原点对称的点在第一象限,说明点M在第三象限,则3m<0,即m<0.
答案:m<0
4.已知点A(2m,-3)与B(6,1-n)关于原点对称,求出m和n的值.
答案:因为点A、B关于原点对称,所以解得m=-3,n=-2.
5.在平面直角坐标系中,点A(5,-2)与点B(2,2)的距离是____________.
思路解析:根据点坐标的几何意义,推出AB==5.
答案:5
6.如果点P(x,y)关于原点的对称点为(-2,3),则x+y=____________.
思路解析:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y),所以x=2,y=-3.则x+y=-1.
答案:-1
7.如果点A(-3,2m+1)关于原点对称的点在第四象限,求m的取值范围.
思路分析:由于第四象限关于 ( http: / / www.21cnjy.com )原点对称的点在第二象限,反之第二象限的点关于原点对称的点在第四象限,所以A(-3,2m+1)应在第二象限,由第二象限的符号特征解之.
解:∵A(-3,2m+1)关于原点对称的点在第四象限,
∴A(-3,2m+1)在第二象限.∴A点的纵坐标2m+1>0.∴m>-.
8.如图23-2-3-3,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-3
作法:两个点关于原点对称时,它们坐标符 ( http: / / www.21cnjy.com )号相反,即P(x,y)关于原点的对称点为P′(-x,-y).因此四边形ABCD的四个顶点A(-2,3)、B(-4,1)、C(-3,-1)、D(-1,0)关于原点的对称点分别为A′(2,-3)、B′(4,-1)、C′(3,1)、D′(1,0),依次连接A′B′、B′C′、C′D′、D′A′,就可得到与四边形ABCD关于原点对称的四边形A′B′C′D′.
( http: / / www.21cnjy.com )
9.直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.
( http: / / www.21cnjy.com )
图23-2-3-4
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形
解:(1)点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原点左侧.
当T1O=P′O=时,△P′TO是等腰三角形,
∴点T1(-,0).
(b)动点T在原点右侧.
①当T2O=T2P′时,△P′TO是等腰三角形,得T2(,0).
②当T3O=P′O时,△P′TO是等腰三角形,得点T3(,0).
③当T4P′=P′O时,△P′TO是等腰三角形,得点T4(4,0).
综上所述,符合条件的t的值为-,,,4.
一、填空题
1.填空:两个点关于原点对称时,它们坐标符号__________,即P(x,y)关于原点的对称点为____________.
2.点P(5,-6)关于y轴对称的点的坐标是____________.
3.已知点P1(a,3)与P2(5,-3)关于原点对称,则a=______________.
4.已知点A1(4,3)与A2(-4,y)关于原点对称,则y=______________.
5.已知点M(-,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
6.已知点A(2m,-3)与B(6,1-n)关于原点对称,求出m和n的值.
7.在平面直角坐标系中,点A(5,-2)与点B(2,2)的距离是____________.
8.如果点P(x,y)关于原点的对称点为(-2,3),则x+y=____________.
9.已知点P(m-1,2)与点Q(1,2)关于y轴对称,那么m=______________.
二、选择题
10.下列说法正确的是 ( )
A.点P(4,-4)关于原点的对称点为P′(-4,-4)
B.点P(4,-4)关于原点的对称点为P′(4,-4)
C.点P(4,-4)关于原点的对称点为P′(-4,4)
D.点P(4,-4)关于原点的对称点为P′(4,4)
三.解答题
11.写出下列已知点关于原点O的对称点的坐标.
A(-2,3),B(5,-5),C(-3,-7),D(3,-2),E(4,6).
12.下列各点中哪两个点关于原点O对称?
A(3,-4),B(-4,5),C(6,-3),D(3,4),E(4,-5),F(-6,3),G(-3,4).
13.如图23-2-3-2,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-2
14.如果点A(-3,2m+1)关于原点对称的点在第四象限,求m的取值范围.
15.如图23-2-3-3,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-3
16.直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.
( http: / / www.21cnjy.com )
图23-2-3-4
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形
17.如图23-2-3-1,利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-1
一、课前预习 (5分钟训练)
1.填空:两个点关于原点对称时,它们坐标符号___________,即P(x,y)关于原点的对称点为____________.
思路解析:根据归纳:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y).
答案:相反 P′(-x,-y)
2.写出下列已知点关于原点O的对称点的坐标.
A(3,0),B(0,-2),C(-1,4),D(-3,-2),E(2,3).
答案:A(3,0)关于原点的对称点为A′(-3,0);B(0,-2)关于原点的对称点为B′(0,2);C(-1,4)关于原点的对称点为C′(1,-4);D(-3,-2)关于原点的对称点为D′(3,2);E(2,3)关于原点的对称点为E′(-2,-3).
3.已知点P(m-1,2)与点Q(1,2)关于y轴对称,那么m=______________.
思路解析:两点关于y轴对称,纵坐标不变,横坐标互为相反数,即m-1+1=0,∴m=0.
答案:0
4.如图23-2-3-1,利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-1
思路分析:利用关于原点对称的点的坐标的特点,先找到三角形各顶点的对应点,再首尾相连即可.
作法:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y).因此△ABC的三个顶点A(-2,2)、B(-4,-1)、C(1,1)关于原点的对称点分别为A′(2,-2)、B′(4,1)、C′(-1,-1),依次连接A′B′、B′C′、A′C′,就可得到与△ABC关于原点对称的△A′B′C′.
( http: / / www.21cnjy.com )
二、课中强化(10分钟训练)
1.写出下列已知点关于原点O的对称点的坐标.
A(-2,3),B(5,-5),C(-3,-7),D(3,-2),E(4,6).
答案:A(-2,3)关于原点的对称点为A ( http: / / www.21cnjy.com )′(2,-3);B(5,-5)关于原点的对称点为B′(-5,5);C(-3,-7)关于原点的对称点为C′(3,7);D(3,-2)关于原点的对称点为D′(-3,2);E(4,6)关于原点的对称点为E′(-4,-6).
2.下列各点中哪两个点关于原点O对称?
A(3,-4),B(-4,5),C(6,-3),D(3,4),E(4,-5),F(-6,3),G(-3,4).
答案:A(3,-4)与G(-3,4);B(-4,5)与E(4,-5);C(6,-3)与F(-6,3).
3.点P(5,-6)关于y轴对称的点的坐标是____________.
思路分析:由点坐标的几何意义可得(-5,-6).
答案:(-5,-6)
4.已知点P1(a,3)与P2(5,-3)关于原点对称,则a=______________.
答案:-5
5.如图23-2-3-2,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-2
思路分析:先找到线段两个端点的对应点,再连结即可.
作法:两个点关于原点对称时,它们坐标符号相 ( http: / / www.21cnjy.com )反,即P(x,y)关于原点的对称点为P′(-x,-y).因此AB的两个端点A(1,3)、B(-2,1)关于原点的对称点分别为A′(-1,-3)、B′(2,-1),连结A′B′,就可得到与AB关于原点对称的A′B′.
( http: / / www.21cnjy.com )
三、课后巩固(30分钟训练)
1.下列说法正确的是 ( )
A.点P(4,-4)关于原点的对称点为P′(-4,-4)
B.点P(4,-4)关于原点的对称点为P′(4,-4)
C.点P(4,-4)关于原点的对称点为P′(-4,4)
D.点P(4,-4)关于原点的对称点为P′(4,4)
答案:C
2.已知点A1(4,3)与A2(-4,y)关于原点对称,则y=______________.
答案:-3
3.已知点M(-,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
思路解析:这道题考查对称点的特点,关于原点 ( http: / / www.21cnjy.com )对称的点,它们的横纵坐标互为相反数,与点M关于原点对称的点在第一象限,说明点M在第三象限,则3m<0,即m<0.
答案:m<0
4.已知点A(2m,-3)与B(6,1-n)关于原点对称,求出m和n的值.
答案:因为点A、B关于原点对称,所以解得m=-3,n=-2.
5.在平面直角坐标系中,点A(5,-2)与点B(2,2)的距离是____________.
思路解析:根据点坐标的几何意义,推出AB==5.
答案:5
6.如果点P(x,y)关于原点的对称点为(-2,3),则x+y=____________.
思路解析:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y),所以x=2,y=-3.则x+y=-1.
答案:-1
7.如果点A(-3,2m+1)关于原点对称的点在第四象限,求m的取值范围.
思路分析:由于第四象限关于 ( http: / / www.21cnjy.com )原点对称的点在第二象限,反之第二象限的点关于原点对称的点在第四象限,所以A(-3,2m+1)应在第二象限,由第二象限的符号特征解之.
解:∵A(-3,2m+1)关于原点对称的点在第四象限,
∴A(-3,2m+1)在第二象限.∴A点的纵坐标2m+1>0.∴m>-.
8.如图23-2-3-3,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.
( http: / / www.21cnjy.com )
图23-2-3-3
作法:两个点关于原点对称时,它们坐标符 ( http: / / www.21cnjy.com )号相反,即P(x,y)关于原点的对称点为P′(-x,-y).因此四边形ABCD的四个顶点A(-2,3)、B(-4,1)、C(-3,-1)、D(-1,0)关于原点的对称点分别为A′(2,-3)、B′(4,-1)、C′(3,1)、D′(1,0),依次连接A′B′、B′C′、C′D′、D′A′,就可得到与四边形ABCD关于原点对称的四边形A′B′C′D′.
( http: / / www.21cnjy.com )
9.直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.
( http: / / www.21cnjy.com )
图23-2-3-4
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形
解:(1)点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原点左侧.
当T1O=P′O=时,△P′TO是等腰三角形,
∴点T1(-,0).
(b)动点T在原点右侧.
①当T2O=T2P′时,△P′TO是等腰三角形,得T2(,0).
②当T3O=P′O时,△P′TO是等腰三角形,得点T3(,0).
③当T4P′=P′O时,△P′TO是等腰三角形,得点T4(4,0).
综上所述,符合条件的t的值为-,,,4.
同课章节目录
