19.2.2一次函数提高习题(有难度)
文档属性
| 名称 | 19.2.2一次函数提高习题(有难度) |  | |
| 格式 | zip | ||
| 文件大小 | 285.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-02 14:28:35 | ||
图片预览


文档简介
19.2.2一次函数 提高练习
一、填空题
1、已知是整数,且一次函数的图象不过第二象限,则为 .
2、若直线和直线的交点坐标为,则 .
3、在同一直角坐标系内,直线与直线都经过点 .
4、当满足 时,一次函数的图象与轴交于负半轴.
5、函数,如果,那么的取值范围是 .
6、一个长,宽的长方形场地要扩建成一个正方形场地,设长增加,宽增加,则与的函数关系是 .自变量的取值范围是 .
7、如图是函数的一部分图像,(1)自变量的取值范围是 ;
(2)当取 时,的最小值为 ;(3)在(1)中的取值范围内,
随的增大而 .
8、已知函数y=(k-1)x+k2-1,当k_______时,它是一次函数,当k=_______时,
它是正比例函数.
9、已知一次函数的图象经过点,且它与轴的交点和直线 与轴的交点关于轴对称,那么这个一次函数的解析式为 .
10、一次函数的图象过点和两点,且,则 ,的取值范围是 .
11、一次函数的图象如图,则与的大小关系是 ,
当 时,是正比例函数.
12、为 时,直线与直线的交点在轴上.
13、已知直线与直线的交点在第三象限内,则的取值范围是 .
14、要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
二、选择题
1、图3中,表示一次函数与正比例函数、是常数,且的图象的是( )
2、直线经过一、二、四象限,则直线的图象只能是图4中的( )
3、若直线与的交点在轴上,那么等于( )
4、直线如图5,则下列条件正确的是( )
5、直线经过点,,则必有( )
A.
6、如果,,则直线不通过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7、已知关于的一次函数在上的函数值总是正数,则的取值范围是( )
A. B. C. D.都不对
8、如图6,两直线和在同一坐标系内图象的位置可能是( )
图6
9、已知一次函数与的图像都经过,且与轴分别交于点B,C,则 的面积为( )
A.4 B.5 C.6 D.7
10、已知直线与轴的交点在轴的正半轴,下列结论:① ;②;③;④,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
11、已知,那么的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
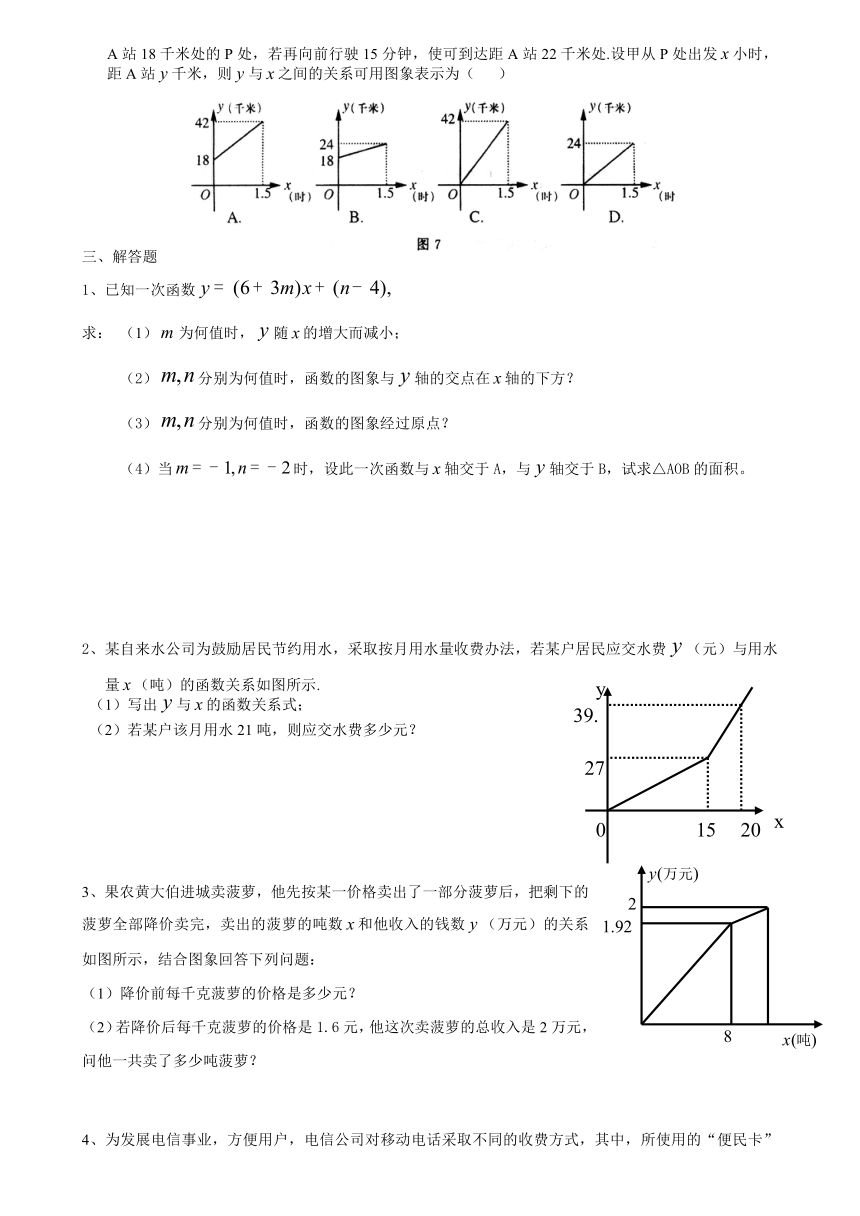
12、如图7,A、B两站相距42千米,甲骑自行车匀速行驶,由A站经P处去B站,上午8时,甲位于距A站18千米处的P处,若再向前行驶15分钟,使可到达距A站22千米处.设甲从P处出发小时,距A站千米,则与之间的关系可用图象表示为( )
三、解答题
1、已知一次函数
求: (1)为何值时,随的增大而减小;
(2)分别为何值时,函数的图象与轴的交点在轴的下方?
(3)分别为何值时,函数的图象经过原点?
(4)当时,设此一次函数与轴交于A,与轴交于B,试求△AOB的面积。
2、某自来水公司为鼓励居民节约用水,采取按月用水量收费办法,若某户居民应交水费(元)与用水量(吨)的函数关系如图所示.
(1)写出与的函数关系式;
(2)若某户该月用水21吨,则应交水费多少元?
3、果农黄大伯进城卖菠萝,他先按某一价格卖出了一部分菠萝后,把剩下的菠萝全部降价卖完,卖出的菠萝的吨数和他收入的钱数(万元)的关系如图所示,结合图象回答下列问题:
(1)降价前每千克菠萝的价格是多少元?
(2)若降价后每千克菠萝的价格是1.6元,他这次卖菠萝的总收入是2万元,问他一共卖了多少吨菠萝?
4、为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在玉溪市范围内每月(30天)的通话时间(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费(便民卡)、 (如意卡)与通话时间之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜?
5、气温随着高度的增加而下降,下降的规律 ( http: / / www.21cnjy.com )是从地面到高空11km处,每升高1 km,气温下降6℃.高于11km时,气温几乎不再变化,设地面的气温为38℃,高空中xkm的气温为y℃.
(1)当0≤x≤11时,求y与x之间的关系式?
(2)求当x=2、5、8、11时,y的值。
(3)求在离地面13 km的高空处、气温是多少度?
(4)当气温是一16℃时,问在离地面多高的地方?
6、小明用的练习本可在甲、乙两个商店内买到 ( http: / / www.21cnjy.com ),已知两个商店的标价都是每个练习本1元,但甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:从第1本开始就按标价的85%卖.
(1)小明要买20个练习本,到哪个商店购买较省钱?
(2)写出甲、乙两个商店中,收款y(元)关于购买本数x(本)(x>10)的关系式。
(3)小明现有24元钱,最多可买多少个本子?
7、如图8,在直角坐标系内,一次函数的图象分别与轴、轴和直线相交于、、三点,直线与轴交于点D,四边形OBCD(O是坐标原点)的面积是10,若点A的横坐标是,求这个一次函数解析式.
8、某油库有一大型储油罐,在开始的8分钟内 ( http: / / www.21cnjy.com ),只开进油管,不开出油管,油罐的油进至24吨(原油罐没储油)后将进油管和出油管同时打开16分钟,油罐内的油从24吨增至40吨,随后又关闭进油管,只开出油管,直到将油罐内的油放完,假设在单位时间内进油管与出油管的流量分别保持不变.
(1)试分别写出这一段时间内油的储油量Q(吨)与进出油的时间t(分)的函数关系式.
(2)在同一坐标系中,画出这三个函数的图象.
9、某市电力公司为了鼓励居 ( http: / / www.21cnjy.com )民用电,采用分段计费的方法计算电费:每月不超过100度时,按每度0.57元计费;每月用电超过100度时,其中的100度按原标准收费;超过部分按每度0.50元计费.
(1)设用电度时,应交电费元,当≤100和>100时,分别写出关于的函数关系式.
(2)小王家第一季度交纳电费情况如下:
月份 一月份 二月份 三月份 合计
交费金额 76元 63元 45元6角 184元6角
问小王家第一季度共用电多少度?
10、某地上年度电价为0.8元,年用电量为1亿度.本年度计划将电价调至0.55~0.75元之间,经测算,若电价调至元,则本年度新增用电量(亿度)与(—0.4)(元)成反比例,又当=0.65时,=0.8.
(1)求与之间的函数关系式;
(2)若每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加20%?[收益=用电量×(实际电价-成本价)]
11、汽车从A站经B站后匀速开往C站,已知离开B站9分钟时,汽车离A站10千米,又行驶一刻钟,离A站20千米.
(1)写出汽车与B站距离与B站开出时间的关系;
(2)如果汽车再行驶30分钟,离A站多少千米?
12、甲乙两个仓库要向A、B两地运送水 ( http: / / www.21cnjy.com )泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两库到A,B两地的路程和运费如下表(表中运费栏“元/(吨、千米)”表示每吨水泥运送1千米所需人民币)
路程/千米 运费(元/吨、千米)
甲库 乙库 甲库 乙库
A地 20 15 12 12
B地 25 20 10 8
(1)设甲库运往A地水泥吨,求总运费(元)关于(吨)的函数关系式,画出它的图象(草图).
(2)当甲、乙两库各运往A、B两地多少吨水泥时,总运费最省?最省的总运费是多少?
0
y
x
15
20
27
39.5
8
2
1.92
一、填空题
1、已知是整数,且一次函数的图象不过第二象限,则为 .
2、若直线和直线的交点坐标为,则 .
3、在同一直角坐标系内,直线与直线都经过点 .
4、当满足 时,一次函数的图象与轴交于负半轴.
5、函数,如果,那么的取值范围是 .
6、一个长,宽的长方形场地要扩建成一个正方形场地,设长增加,宽增加,则与的函数关系是 .自变量的取值范围是 .
7、如图是函数的一部分图像,(1)自变量的取值范围是 ;
(2)当取 时,的最小值为 ;(3)在(1)中的取值范围内,
随的增大而 .
8、已知函数y=(k-1)x+k2-1,当k_______时,它是一次函数,当k=_______时,
它是正比例函数.
9、已知一次函数的图象经过点,且它与轴的交点和直线 与轴的交点关于轴对称,那么这个一次函数的解析式为 .
10、一次函数的图象过点和两点,且,则 ,的取值范围是 .
11、一次函数的图象如图,则与的大小关系是 ,
当 时,是正比例函数.
12、为 时,直线与直线的交点在轴上.
13、已知直线与直线的交点在第三象限内,则的取值范围是 .
14、要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
二、选择题
1、图3中,表示一次函数与正比例函数、是常数,且的图象的是( )
2、直线经过一、二、四象限,则直线的图象只能是图4中的( )
3、若直线与的交点在轴上,那么等于( )
4、直线如图5,则下列条件正确的是( )
5、直线经过点,,则必有( )
A.
6、如果,,则直线不通过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7、已知关于的一次函数在上的函数值总是正数,则的取值范围是( )
A. B. C. D.都不对
8、如图6,两直线和在同一坐标系内图象的位置可能是( )
图6
9、已知一次函数与的图像都经过,且与轴分别交于点B,C,则 的面积为( )
A.4 B.5 C.6 D.7
10、已知直线与轴的交点在轴的正半轴,下列结论:① ;②;③;④,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
11、已知,那么的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12、如图7,A、B两站相距42千米,甲骑自行车匀速行驶,由A站经P处去B站,上午8时,甲位于距A站18千米处的P处,若再向前行驶15分钟,使可到达距A站22千米处.设甲从P处出发小时,距A站千米,则与之间的关系可用图象表示为( )
三、解答题
1、已知一次函数
求: (1)为何值时,随的增大而减小;
(2)分别为何值时,函数的图象与轴的交点在轴的下方?
(3)分别为何值时,函数的图象经过原点?
(4)当时,设此一次函数与轴交于A,与轴交于B,试求△AOB的面积。
2、某自来水公司为鼓励居民节约用水,采取按月用水量收费办法,若某户居民应交水费(元)与用水量(吨)的函数关系如图所示.
(1)写出与的函数关系式;
(2)若某户该月用水21吨,则应交水费多少元?
3、果农黄大伯进城卖菠萝,他先按某一价格卖出了一部分菠萝后,把剩下的菠萝全部降价卖完,卖出的菠萝的吨数和他收入的钱数(万元)的关系如图所示,结合图象回答下列问题:
(1)降价前每千克菠萝的价格是多少元?
(2)若降价后每千克菠萝的价格是1.6元,他这次卖菠萝的总收入是2万元,问他一共卖了多少吨菠萝?
4、为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在玉溪市范围内每月(30天)的通话时间(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费(便民卡)、 (如意卡)与通话时间之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜?
5、气温随着高度的增加而下降,下降的规律 ( http: / / www.21cnjy.com )是从地面到高空11km处,每升高1 km,气温下降6℃.高于11km时,气温几乎不再变化,设地面的气温为38℃,高空中xkm的气温为y℃.
(1)当0≤x≤11时,求y与x之间的关系式?
(2)求当x=2、5、8、11时,y的值。
(3)求在离地面13 km的高空处、气温是多少度?
(4)当气温是一16℃时,问在离地面多高的地方?
6、小明用的练习本可在甲、乙两个商店内买到 ( http: / / www.21cnjy.com ),已知两个商店的标价都是每个练习本1元,但甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:从第1本开始就按标价的85%卖.
(1)小明要买20个练习本,到哪个商店购买较省钱?
(2)写出甲、乙两个商店中,收款y(元)关于购买本数x(本)(x>10)的关系式。
(3)小明现有24元钱,最多可买多少个本子?
7、如图8,在直角坐标系内,一次函数的图象分别与轴、轴和直线相交于、、三点,直线与轴交于点D,四边形OBCD(O是坐标原点)的面积是10,若点A的横坐标是,求这个一次函数解析式.
8、某油库有一大型储油罐,在开始的8分钟内 ( http: / / www.21cnjy.com ),只开进油管,不开出油管,油罐的油进至24吨(原油罐没储油)后将进油管和出油管同时打开16分钟,油罐内的油从24吨增至40吨,随后又关闭进油管,只开出油管,直到将油罐内的油放完,假设在单位时间内进油管与出油管的流量分别保持不变.
(1)试分别写出这一段时间内油的储油量Q(吨)与进出油的时间t(分)的函数关系式.
(2)在同一坐标系中,画出这三个函数的图象.
9、某市电力公司为了鼓励居 ( http: / / www.21cnjy.com )民用电,采用分段计费的方法计算电费:每月不超过100度时,按每度0.57元计费;每月用电超过100度时,其中的100度按原标准收费;超过部分按每度0.50元计费.
(1)设用电度时,应交电费元,当≤100和>100时,分别写出关于的函数关系式.
(2)小王家第一季度交纳电费情况如下:
月份 一月份 二月份 三月份 合计
交费金额 76元 63元 45元6角 184元6角
问小王家第一季度共用电多少度?
10、某地上年度电价为0.8元,年用电量为1亿度.本年度计划将电价调至0.55~0.75元之间,经测算,若电价调至元,则本年度新增用电量(亿度)与(—0.4)(元)成反比例,又当=0.65时,=0.8.
(1)求与之间的函数关系式;
(2)若每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加20%?[收益=用电量×(实际电价-成本价)]
11、汽车从A站经B站后匀速开往C站,已知离开B站9分钟时,汽车离A站10千米,又行驶一刻钟,离A站20千米.
(1)写出汽车与B站距离与B站开出时间的关系;
(2)如果汽车再行驶30分钟,离A站多少千米?
12、甲乙两个仓库要向A、B两地运送水 ( http: / / www.21cnjy.com )泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两库到A,B两地的路程和运费如下表(表中运费栏“元/(吨、千米)”表示每吨水泥运送1千米所需人民币)
路程/千米 运费(元/吨、千米)
甲库 乙库 甲库 乙库
A地 20 15 12 12
B地 25 20 10 8
(1)设甲库运往A地水泥吨,求总运费(元)关于(吨)的函数关系式,画出它的图象(草图).
(2)当甲、乙两库各运往A、B两地多少吨水泥时,总运费最省?最省的总运费是多少?
0
y
x
15
20
27
39.5
8
2
1.92
