15.1.4整式的乘法第二课时(浙江省台州市临海市)
文档属性
| 名称 | 15.1.4整式的乘法第二课时(浙江省台州市临海市) |

|
|
| 格式 | rar | ||
| 文件大小 | 714.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-07 00:00:00 | ||
图片预览




文档简介
课件15张PPT。15.1.4 整式的乘法2 多项式与多项式相乘回顾与思考② 再把所得的积相加。① 将单项式分别乘以多项式的各项,① 不能漏乘:即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.基本功训练:
-(a2b)3.(-ab2)4
(-6a3) .(5a2- a+1)
= -a10b11
= - 30a5+4a4-6a3
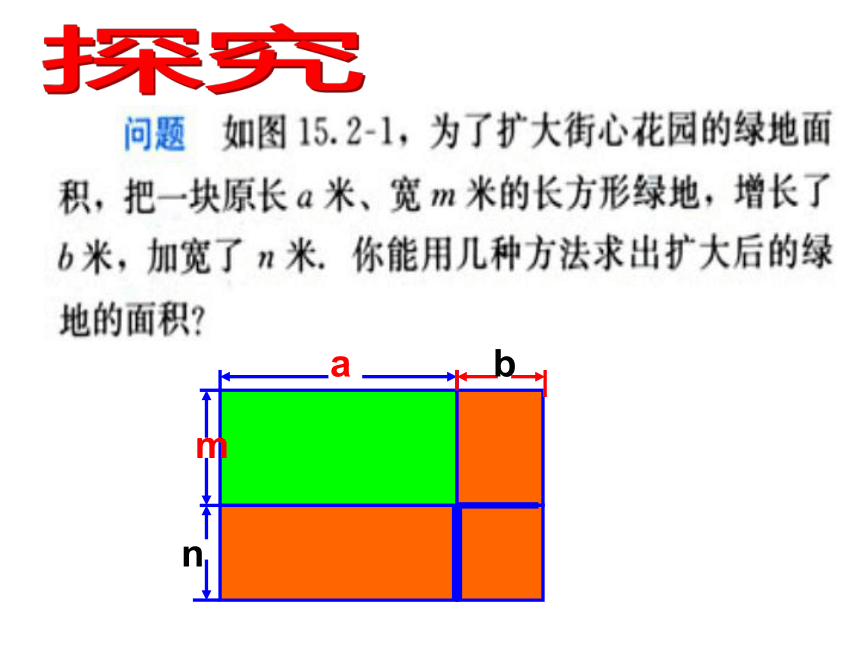
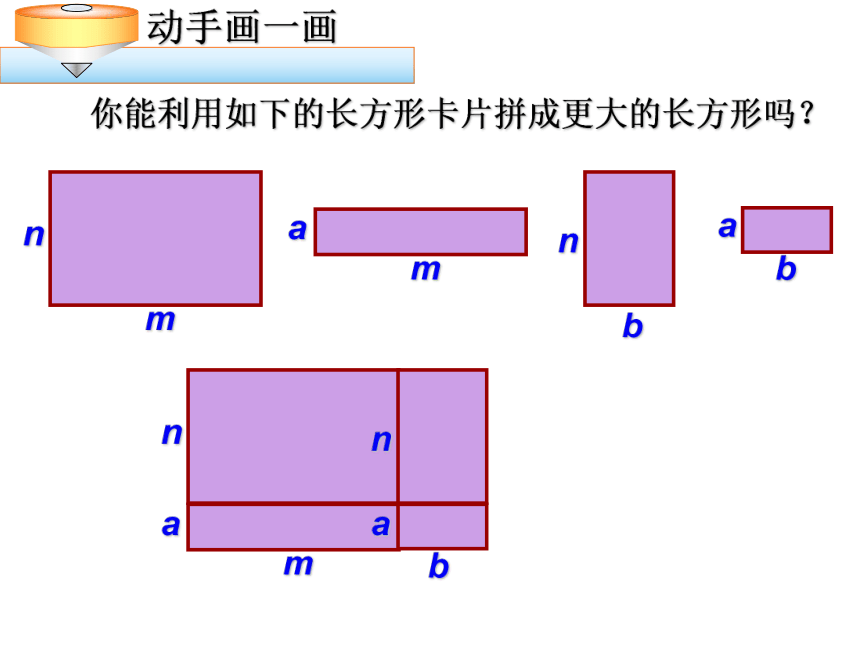
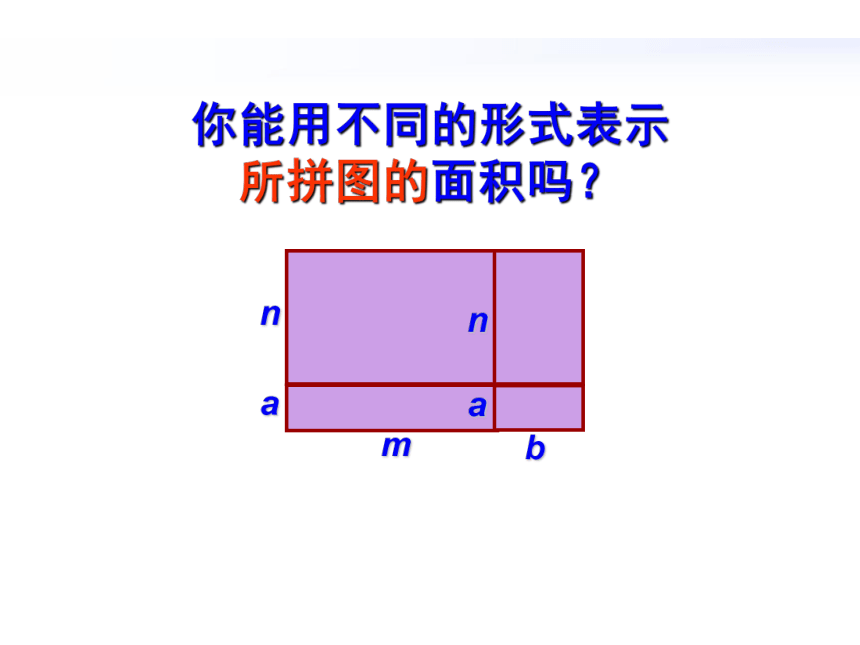
探究 你能利用如下的长方形卡片拼成更大的长方形吗?mnmabnba 你能用不同的形式表示 所拼图的面积吗?(a+b)(m+n)=am+ an+ bm+ bn如何进行多项式与多项式相乘的 运算 ?先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。例题解析 【例1】计算: (1)(1?x)(0.6?x), (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:负负得正
一正一负得负。 ?最后的结果要合并同类项. (3)(3x+1)(x-2) (4) (x - 8y)(x-y)(5) (x+y)(2x–y)(3x+2y).(1) (x+y)2例2、计算(3) (2a+b)2;(4) (x–1)(x2+x+1) ;(2) (x+y)(x2y+y2)例3 计算:(1) (x+y)(x–y);(2) (x+y)(x2–xy+y2)解:(1) (x+y)(x–y)=x2 (2) (x+y)(x2–xy+y2)
=x3 =x3 =x2–xy+xy–y2
–y2.
–x2y+xy2+x2y–xy2+y3
+y3 你注意到了吗? 多项式乘以多项式,展开后项数很有规律,在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积。本节课你的收获是什么?本节课你学到了什么?合并同类项. 小 结(a+ b) (m +n)= am+ bm+ an+ bn(a+ b+c) (m +n)= am+an+bm+bn+cm+cn多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.多项式与多项式相乘的法则:作业(1) (2a–3b)(a+5b) ;(2) (xy–z)(2xy+z) ;(3) (x–1)(x2+x+1) ;(4) (2a+b)2;(5) (3a–2)(a–1)–(a+1)(a+2) ;(6) (x+y)(2x–y)(3x+2y).
-(a2b)3.(-ab2)4
(-6a3) .(5a2- a+1)
= -a10b11
= - 30a5+4a4-6a3
探究 你能利用如下的长方形卡片拼成更大的长方形吗?mnmabnba 你能用不同的形式表示 所拼图的面积吗?(a+b)(m+n)=am+ an+ bm+ bn如何进行多项式与多项式相乘的 运算 ?先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。例题解析 【例1】计算: (1)(1?x)(0.6?x), (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:负负得正
一正一负得负。 ?最后的结果要合并同类项. (3)(3x+1)(x-2) (4) (x - 8y)(x-y)(5) (x+y)(2x–y)(3x+2y).(1) (x+y)2例2、计算(3) (2a+b)2;(4) (x–1)(x2+x+1) ;(2) (x+y)(x2y+y2)例3 计算:(1) (x+y)(x–y);(2) (x+y)(x2–xy+y2)解:(1) (x+y)(x–y)=x2 (2) (x+y)(x2–xy+y2)
=x3 =x3 =x2–xy+xy–y2
–y2.
–x2y+xy2+x2y–xy2+y3
+y3 你注意到了吗? 多项式乘以多项式,展开后项数很有规律,在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积。本节课你的收获是什么?本节课你学到了什么?合并同类项. 小 结(a+ b) (m +n)= am+ bm+ an+ bn(a+ b+c) (m +n)= am+an+bm+bn+cm+cn多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.多项式与多项式相乘的法则:作业(1) (2a–3b)(a+5b) ;(2) (xy–z)(2xy+z) ;(3) (x–1)(x2+x+1) ;(4) (2a+b)2;(5) (3a–2)(a–1)–(a+1)(a+2) ;(6) (x+y)(2x–y)(3x+2y).
