沪科版2023-2024八年级上期末模拟试题2(含解析)
文档属性
| 名称 | 沪科版2023-2024八年级上期末模拟试题2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 16:58:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版2023-2024八年级上期末模拟试题2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
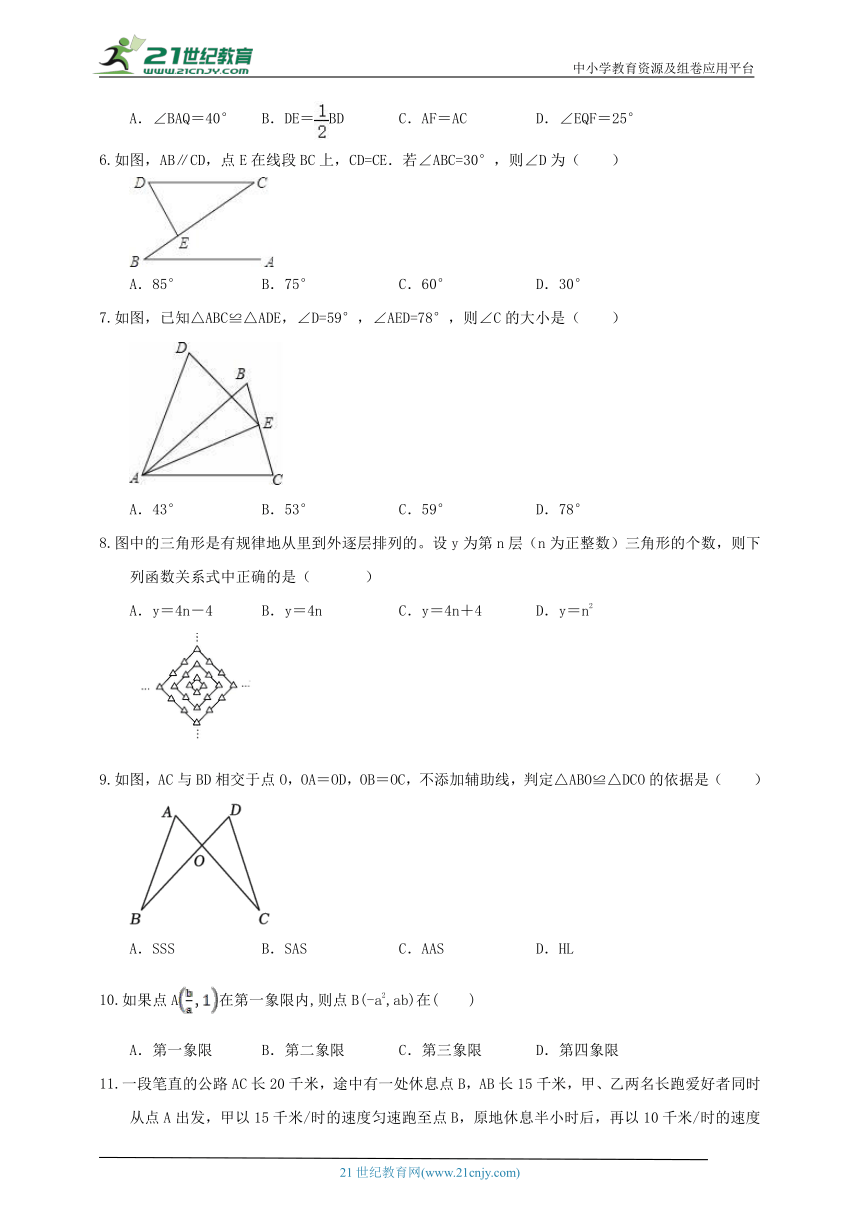
函数y=的自变量x的取值范围是( )
A.x<2 B.x≤2 C.x>2 D.x≥2
下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm
C.3cm,4cm,8cm D.3cm,3cm,4cm
如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )
A.(2,3) B.(0,3) C.(3,2) D.(2,2)
如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
A.1 B. C. D.2
如图,△ABC中,若∠BAC=80°,∠ACB=70°,根据图中尺规作图的痕迹推断,以下结论错误的是( )
A.∠BAQ=40° B.DE=BD C.AF=AC D.∠EQF=25°
如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
如图,已知△ABC≌△ADE,∠D=59°,∠AED=78°,则∠C的大小是( )
A.43° B.53° C.59° D.78°
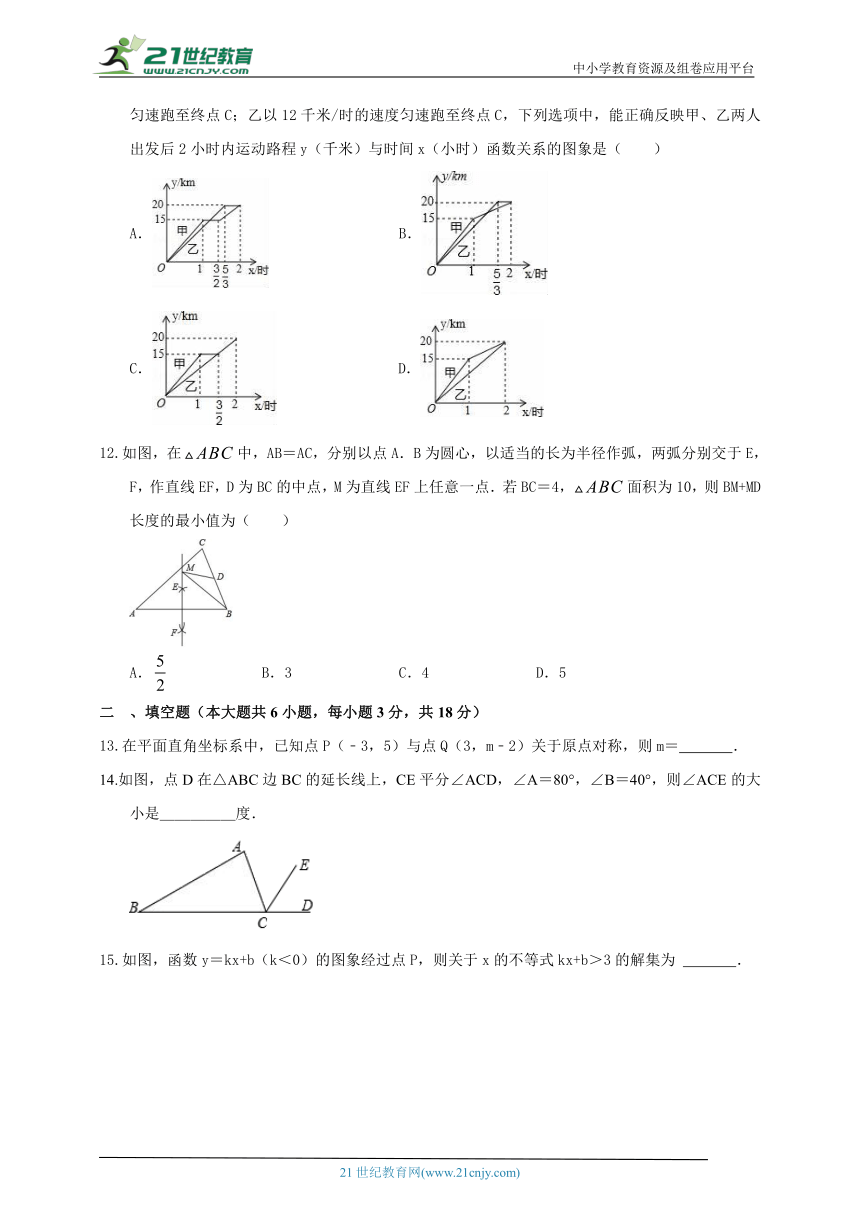
图中的三角形是有规律地从里到外逐层排列的。设y为第n层(n为正整数)三角形的个数,则下列函数关系式中正确的是( )
A.y=4n-4 B.y=4n C.y=4n+4 D.y=n2
如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
A.SSS B.SAS C.AAS D.HL
如果点A在第一象限内,则点B(-a2,ab)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A. B.
C. D.
如图,在中,AB=AC,分别以点A.B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
1 、填空题(本大题共6小题,每小题3分,共18分)
在平面直角坐标系中,已知点P(﹣3,5)与点Q(3,m﹣2)关于原点对称,则m= .
如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是_____度.
如图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为 .
如图,,,请添加一个条件______,使.
如图是平面直角坐标系中的一组直线,按此规律推断,第5条直线与x轴交点的横坐标是 .
如图,在三角形纸片ABC中,AB=AC,∠B=20°,点D是边BC上的动点,将三角形纸片沿AD对折,使点B落在点B′处,当B′D⊥BC时,∠BAD的度数为 .
1 、解答题(本大题共8小题,共66分)
已知三角形的三边长分别为a,b,c,化简:|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|.
如图,在正方形中,点在边的延长线上,点在边的延长线上,且,连接和相交于点.
求证: .
在平面直角坐标系中,已知点A(﹣2,0)、B(0,3),O为原点.
(1)求三角形AOB的面积;
(2)若点C在坐标轴上,且三角形ABC的面积为6,求点C的坐标.
如图,在△ABC中,分别画出:
(1)AB边上的高CD;
(2)AC边上的高BE;
(3)∠C的角平分线CF;
(4)BC上的中线AM.
5月18日,我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.
(1)求每盒口罩和每盒水银体温计的价格各是多少元?
(2)如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.
(3)在民联药店累计购医用品超过1800元后,超出1800元的部分可享受8折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.若该校九年级有900名学生,需要购买口罩和水银体温计各多少盒?所需总费用为多少元?
学校需要添置教师办公桌椅A.B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60°,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
答案解析
1 、选择题
【考点】二次根式有意义的条件,函数自变量的取值范围
【分析】本题主要考查自变量的取值范围,函数关系中主要有二次根式,根据二次根式的意义,被开方数是非负数.
解:根据题意得:2x﹣4≥0,
解得x≥2.
故选:D.
【点评】函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数,
(2)当函数表达式是分式时,考虑分式的分母不能为0,
(3)当函数表达式是二次根式时,被开方数为非负数.
【考点】三角形三边关系.
【分析】依据三角形任意两边之和大于第三边求解即可.
解:A.因为2+3=5,所以不能构成三角形,故A错误;
B、因为2+4<6,所以不能构成三角形,故B错误;
C、因为3+4<8,所以不能构成三角形,故C错误;
D、因为3+3>4,所以能构成三角形,故D正确.
故选:D.
【点评】本题考查了全等三角形的性质;熟练掌握全等三角形的对应角相等的性质是解决问题的关键.
【考点】坐标确定位置.
【分析】根据平面直角坐标系写出博物馆的坐标即可.
解:由图可知,博物馆的坐标为(2,2).
故选D.
【点评】本题考查了坐标确定位置,熟练掌握平面直角坐标系中点的坐标的写法是解题的关键.
【考点】 三角形的重心; 等腰直角三角形.
【分析】连接CP并延长,交AB于D,根据重心的性质得到CD是△ABC的中线,PD=CD,根据直角三角形的性质求出CD,计算即可.
解:连接CP并延长,交AB于D,
∵P是Rt△ABC的重心,
∴CD是△ABC的中线,PD=CD,
∵∠C=90°,
∴CD=AB=3,
∵AC=BC,CD是△ABC的中线,
∴CD⊥AB,
∴PD=1,即点P到AB所在直线的距离等于1,
故选:A.
【考点】作图—基本作图.
【分析】根据线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质判断即可.
解:A.由作图可知,AQ平分∠BAC,
∴∠BAP=∠CAP=∠BAC=40°,
故选项A正确,不符合题意,
B.由作图可知,MQ是BC的垂直平分线,
∴∠DEB=90°,
∵∠B=30°,
∴DE=BD,
故选项B正确,不符合题意,
C.∵∠B=30°,∠BAP=40°,
∴∠AFC=70°,
∵∠C=70°,
∴AF=AC,
故选项C正确,不符合题意,
D.∵∠EFQ=∠AFC=70°,∠QEF=90°,
∴∠EQF=20°,
故选项D错误,符合题意.
故选:D.
【点评】本题考查了线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质等知识,解题的关键是读懂图象信息.
【考点】平行线的性质,三角形内角和定理
【分析】先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠CED,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D.
解:∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,
∴∠D=75°.
故选:B.
【点评】此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.
【考点】全等三角形的性质.
【分析】由全等三角形的性质得出对应角相等∠C=∠AED=78°,即可得出结论.
解:∵△ABC≌△ADE,
∴∠C=∠AED=78°;
故选:D.
【点评】本题考查了全等三角形的性质;熟练掌握全等三角形的对应角相等的性质是解决问题的关键.
【考点】函数关系式;规律型:图形的变化类
【分析】根据图示可知,第一层是4个,第二层是8个,第三层是12,…第n层是4n,所以,即可确定y与n的关系.解:由图可知:
n=1时,圆点有4个,即y=4;
n=2时,圆点有8个,即y=8;
所以y=4n.
故选B.
【点评】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.解题关键是根据图形找到点的排列规律.
【考点】全等三角形的判定.
【分析】根据题目中的条件和全等三角形的判定方法,可以得到判定△ABO≌△DCO的依据.
解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
故选:B.
【点评】本题考查全等三角形的判定,解答本题的关键是明确题意,写出△AOB和△DOC全等的证明过程.
【考点】点的坐标特征
【分析】根据第一象限点的横坐标是正数判断出a、b同号,再根据非负数的性质和各象限内点的坐标特征解答.
解:∵点A(,1)在第一象限,
∴>0,
∴a、b同号,
∴-a2<0,ab>0,
∴点B(-a2,ab)在第二象限.
故答案为:B.
【点评】本题考查了各象限内点的坐标的符号特征,解题关键是记住各象限内点的坐标的符号.
【考点】函数的图象.
【分析】分别求出甲乙两人到达C地的时间,再结合已知条件即可解决问题.
解;由题意,甲走了1小时到了B地,在B地休息了半个小时,2小时正好走到C地,乙走了小时到了C地,在C地休息了小时.
由此可知正确的图象是A.
故选A.
【点评】本题考查函数图象、路程.速度、时间之间的关系,解题的关键是理解题意,读懂图象信息解决问题,属于中考常考题型.
【考点】线段垂直平分线的性质,轴对称-最短路线问题
【分析】由基本作图得到得EF垂直平分AB,则MB=MA,所以BM+MD=MA+MD,连接MA.DA,如图,利用两点之间线段最短可判断MA+MD的最小值为AD,再利用等腰三角形的性质得到AD⊥BC,然后利用三角形面积公式计算出AD即可.
解:由作法得EF垂直平分AB,
∴MB=MA,
∴BM+MD=MA+MD,
连接MA.DA,如图,
∵MA+MD≥AD(当且仅当M点在AD上时取等号),
∴MA+MD的最小值为AD,
∵AB=AC,D点为BC的中点,
∴AD⊥BC,
∵
∴
∴BM+MD长度的最小值为5.
故选:D.
【点评】本题考查的是线段的垂直平分线的性质,利用轴对称求线段和的最小值,三角形的面积,两点之间,线段最短,掌握以上知识是解题的关键.
1 、填空题
【考点】关于原点对称的点的坐标.
【分析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),即求关于原点的对称点时,横、纵坐标都变成原数的相反数.
解:根据两个点关于原点对称,则横、纵坐标都是原数的相反数,
得m﹣2=﹣5,
∴m=﹣3.
故答案为:﹣3.
【点评】本题主要考查了平面直角坐标系内两点关于原点的对称点时,横、纵坐标都变成原数的相反数,难度适中.
【考点】三角形的外角性质.
【分析】由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A,然后利用角平分线的定义计算即可.
解:∵∠ACD=∠B+∠A,
而∠A=80°,∠B=4°,
∴∠ACD=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=60°,
故答案为60
【点评】本题考查了三角形的外角定理,关键是根据三角形任意一个外角等于与之不相邻的两内角的和.
【考点】一次函数与一元一次不等式.
【分析】根据函数图象中的数据和一次函数的性质,可以写出等式kx+b>3的解集.
解:由图象可得,
当x=﹣1时,y=3,该函数y随x的增大而减小,
∴不等式kx+b>3的解集为x<﹣1,
故答案为:x<﹣1.
【点评】本题考查一次函数与一元一次不等式,解答本题的关键是明确一次函数与一元一次不等式的关系,利用数形结合的思想解答.
【考点】全等三角形的判定
【分析】根据角边角可证得,即可.
解:可添加∠A=∠D,理由如下:
∵,
∴∠DCE=∠ACB,
∵,∠A=∠D,
∴.
故答案为:∠A=∠D(答案不唯一)
【点评】本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
【考点】一次函数图象上点的坐标特征,规律型:点的坐标.
【分析】根据每条直线与x轴交点的横坐标解答即可.
解:由题知,这组直线是平行直线,每条直线与x轴交点的横坐标依次是2,4,6...,
∴第5条直线与x轴的交点的横坐标是10.
故答案为:10.
【点评】本题考查了一次函数图象上点的坐标特征,掌握一次函数图象上点的坐标特征是解题的关键.
【考点】翻折变换(折叠问题),等腰三角形的性质.
【分析】分两种情况,一是点B′在直线BC的下方,则∠BDB′=90°,所以∠ADB′=∠ADB=135°,则∠BAD=180°﹣∠B﹣∠ADB=25°,二是点B′在直线BC的上方,则∠ADB′=∠ADB=45°,所以∠BAD=180°﹣∠B﹣∠ADB=115°,于是得到问题的答案.
解:当点B′在直线BC的下方,如图1,
∵B′D⊥BC,
∴∠BDB′=90°,
∴∠ADB′+∠ADB=360°﹣90°=270°,
∵将三角形纸片沿AD对折,使点B落在点B′处,
∴∠ADB′=∠ADB=×270°=135°,
∵∠B=20°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣20°﹣135°=25°,
当点B′在直线BC的上方时,如图2,
∵B′D⊥BC,
∴∠BDB′=90°,
∵将三角形纸片沿AD对折,使点B落在点B′处,
∴∠ADB′=∠ADB=×90°=45°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣20°﹣45°=115°,
故答案为:25°或115°.
【点评】此题重点考查等腰三角形的性质、轴对称的性质、三角形内角和定理等知识,正确地求出∠BAB′的度数是解题的关键.
1 、解答题
【考点】三角形三边关系;绝对值
【分析】三角形三边满足的条件是:两边和大于第三边,两边的差小于第三边,根据此条件来确定绝对值内的式子的正负,从而化简计算即可.
解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,则a+b﹣c>0,a﹣b﹣c<0,a+b+c>0,
∴|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|=a+b﹣c+2a﹣2b﹣2c+a+b+c=4a﹣2c.
【点评】此题考查了三角形三边关系,此题的关键是先根据三角形三边的关系来判定绝对值内式子的正负.
【考点】正方形的性质,全等三角形的判定与性质
【分析】利用正方形的性质证明:AB=BC=CD,∠ABE=∠BCF=90°,再证明BE=CF,可得三角形的全等,利用全等三角形的性质可得答案.
证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°,
又∵CE=DF,
∴CE+BC=DF+CD即BE=CF,
在△BCF和△ABE中,
∴(SAS),
∴AE=BF.
【点评】本题考查的是正方形的性质,三角形全等的判定与性质,掌握以上知识是解题的关键.
【考点】坐标与图形性质;三角形的面积.
【分析】(1)直接根据三角形面积公式求解;
(2)设C(0,t),根据三角形面积公式得到 |t﹣3| 2=6,然后解绝对值方程求出t即可得到C点坐标.
解:(1)如图:
S△AOB=×2×3=3;
(2)设C(0,t),
∵三角形ABC的面积为6,
∴ |t﹣3| 2=6,
解得t=9或﹣3.
∴C点坐标为(0,﹣3),(0,9).
【点评】本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了三角形面积公式.
【考点】作图—复杂作图.
【分析】(1)利用基本作图(过一点作已知直线的垂线)作出垂线段CD即可;
(2)利用基本作图(过一点作已知直线的垂线)作出垂线段BE即可;
(3)利用基本作图(过一个角的平分线)作出CF即可;
(4)利用基本作图(作线段的垂直平分线)作出BC的垂直平分线得到BC的中点,则AM为所作.
解:(1)如图,CD为所作;
(2)如图,BE为所作;
(3)如图,CF为所作;
(4)如图,AM为所作.
【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
【考点】分式方程的应用,一次函数的应用
【分析】(1)设每盒水银体温计的价格是x元,根据用1200元购买口罩盒数与用300元购买水银体温计的盒数相同列出方程,求解即可;
(2)先用m表示出需要水银体温计的支数,再表示出水银体温计的盒数;
(3)分当m≤4时,当m>4时,分别得出关系式,再合并,根据若该校九年级有900名学生求出口罩的盒数m,从而得到体温计的盒数以及总费用.
解:(1)设每盒水银体温计的价格是x元,则每盒口罩的价格是x+150元,
根据题意可得:,
解得:x=50,
经检验:x=50是原方程的解,
50+150=200元,
∴每盒口罩和每盒水银体温计的价格各是200元,50元;
(2)∵购买口罩m盒,
∴共有口罩100m个,
∵给每位学生发放2只口罩和1支水银体温计,
∴需要发放支水银体温计,
∴需要购买盒水银体温计;
(3)由题意可得:
令200m+5m×50=1800,
解得:m=4,
若未超过1800元,即当m≤4时,
则w=200m+5m×50=450m,
若超过1800元,即当m>4时,
w=(200m+5m×50-1800)×0.8+1800=360m+360,
∴w关于m的函数关系式为,
若该校九年级有900名学生,即=900,
解得:m=18,
则=6840,
答:需要购买口罩18盒,水银体温计90盒,所需总费用为6840元.
【点评】本题考查了分式方程的实际应用,一次函数的实际应用,解题的关键是理解题意,弄清口罩盒数与体温计盒数的配套关系.
【考点】二元一次方程组的应用;一元一次不等式组的应用;一次函数的应用
【分析】(1)根据“2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元”,建立方程组即可得出结论;
(2)根据题意建立函数关系式,由A型桌椅不少于120套,B型桌椅不少于70套,确定出x的范围;
(3)根据一次函数的性质,即可得出结论.
解:(1)设A型桌椅的单价为a元,B型桌椅的单价为b元,
根据题意知,,
解得,,
即:A,B两型桌椅的单价分别为600元,800元;
(2)根据题意知,y=600x+800(200﹣x)+200×10=﹣200x+162000(120≤x≤130),
(3)由(2)知,y=﹣200x+162000(120≤x≤130),
∴当x=130时,总费用最少,
即:购买A型桌椅130套,购买B型桌椅70套,总费用最少,最少费用为136000元.
【点评】本题考查一次函数的应用,二元一次方程的应用,一元一次不等式组的应用,读懂题意,列出方程组或不等式是解本题的关键.
【考点】坐标与图形性质;三角形的面积.
【分析】(1)根据点的平移规律易得点C,D的坐标;
(2)先计算出S平行四边形ABOC=8,设M坐标为(0,m),根据三角形面积公式得×4×|m|=8,解得m=±4,于是可得M点的坐标为(0,4)或(0,﹣4);
(3)①先计算出S梯形OCDB=7,再讨论:当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP<4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;
②分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO﹣∠EPC=∠BOP﹣∠DCP,于是∠BOP﹣∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
解:(1)由平移可知:C(0,2),D(4,2);
(2)∵AB=4,CO=2,
∴S平行四边形ABOC=AB CO=4×2=8,
设M坐标为(0,m),
∴×4×|m|=8,解得m=±4
∴M点的坐标为(0,4)或(0,﹣4);
(3)①S梯形OCDB=×(3+4)×2=7,
当点P运动到点B时,S△BOC最小,S△BOC的最小值=×3×2=3,S△CDP+S△BOP<4,
当点P运动到点D时,S△BOC最大,S△BOC的最大值=×4×2=4,S△CDP+S△BOP>3,
所以3<S△CDP+S△BOP<4;
②当点P在BD上,如图1,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠EPO﹣∠EPC=∠BOP﹣∠DCP,
∴∠BOP﹣∠DCP=∠CPO;
同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
【点评】 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查三角形面积公式和平行线的性质.
【考点】 等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30角的直角三角形的性质
【分析】 (1)由等腰三角形的性质和已知条件得出∠BAD=∠DAC=×120°=60°,再证出∠ADE=∠ADF=90°﹣60°=30°,由含30角的直角三角形的性质得出AE=AD,AF=AD,即可得出结论;
(2)连接BD,证明△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠ABD=∠DAC,得出∠EDB=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF,即可得出结论.
(1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=∠BAC,
∵∠BAC=120°,
∴∠BAD=∠DAC=×120°=60°,
∵DE⊥AB,DF⊥AC,
∴∠ADE=∠ADF=90°﹣60°=30°,
∴AE=AD,AF=AD,
∴AE+AF=AD+AD=AD;
(2)解:线段AE,AF,AD之间的数量关系为:AE+AF=AD,理由如下:
连接BD,如图所示:
∵∠BAD=60°,AB=AD,
∴△ABD是等边三角形,
∴BD=AD,∠ABD=∠ADB=60°,
∵∠DAC=60°,
∴∠ABD=∠DAC,
∵∠EDB+∠EDA=∠EDA+∠ADF=60°,
∴∠EDB=∠ADF,
在△BDE与△ADF中,,
∴△BDE≌△ADF(ASA),
∴BE=AF,
∵AE+BE=AD,
∴AE+AF=AD.
【点评】本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30角的直角三角形的性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版2023-2024八年级上期末模拟试题2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
函数y=的自变量x的取值范围是( )
A.x<2 B.x≤2 C.x>2 D.x≥2
下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm
C.3cm,4cm,8cm D.3cm,3cm,4cm
如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )
A.(2,3) B.(0,3) C.(3,2) D.(2,2)
如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
A.1 B. C. D.2
如图,△ABC中,若∠BAC=80°,∠ACB=70°,根据图中尺规作图的痕迹推断,以下结论错误的是( )
A.∠BAQ=40° B.DE=BD C.AF=AC D.∠EQF=25°
如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
如图,已知△ABC≌△ADE,∠D=59°,∠AED=78°,则∠C的大小是( )
A.43° B.53° C.59° D.78°
图中的三角形是有规律地从里到外逐层排列的。设y为第n层(n为正整数)三角形的个数,则下列函数关系式中正确的是( )
A.y=4n-4 B.y=4n C.y=4n+4 D.y=n2
如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
A.SSS B.SAS C.AAS D.HL
如果点A在第一象限内,则点B(-a2,ab)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A. B.
C. D.
如图,在中,AB=AC,分别以点A.B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
1 、填空题(本大题共6小题,每小题3分,共18分)
在平面直角坐标系中,已知点P(﹣3,5)与点Q(3,m﹣2)关于原点对称,则m= .
如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是_____度.
如图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为 .
如图,,,请添加一个条件______,使.
如图是平面直角坐标系中的一组直线,按此规律推断,第5条直线与x轴交点的横坐标是 .
如图,在三角形纸片ABC中,AB=AC,∠B=20°,点D是边BC上的动点,将三角形纸片沿AD对折,使点B落在点B′处,当B′D⊥BC时,∠BAD的度数为 .
1 、解答题(本大题共8小题,共66分)
已知三角形的三边长分别为a,b,c,化简:|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|.
如图,在正方形中,点在边的延长线上,点在边的延长线上,且,连接和相交于点.
求证: .
在平面直角坐标系中,已知点A(﹣2,0)、B(0,3),O为原点.
(1)求三角形AOB的面积;
(2)若点C在坐标轴上,且三角形ABC的面积为6,求点C的坐标.
如图,在△ABC中,分别画出:
(1)AB边上的高CD;
(2)AC边上的高BE;
(3)∠C的角平分线CF;
(4)BC上的中线AM.
5月18日,我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.
(1)求每盒口罩和每盒水银体温计的价格各是多少元?
(2)如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.
(3)在民联药店累计购医用品超过1800元后,超出1800元的部分可享受8折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.若该校九年级有900名学生,需要购买口罩和水银体温计各多少盒?所需总费用为多少元?
学校需要添置教师办公桌椅A.B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60°,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
答案解析
1 、选择题
【考点】二次根式有意义的条件,函数自变量的取值范围
【分析】本题主要考查自变量的取值范围,函数关系中主要有二次根式,根据二次根式的意义,被开方数是非负数.
解:根据题意得:2x﹣4≥0,
解得x≥2.
故选:D.
【点评】函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数,
(2)当函数表达式是分式时,考虑分式的分母不能为0,
(3)当函数表达式是二次根式时,被开方数为非负数.
【考点】三角形三边关系.
【分析】依据三角形任意两边之和大于第三边求解即可.
解:A.因为2+3=5,所以不能构成三角形,故A错误;
B、因为2+4<6,所以不能构成三角形,故B错误;
C、因为3+4<8,所以不能构成三角形,故C错误;
D、因为3+3>4,所以能构成三角形,故D正确.
故选:D.
【点评】本题考查了全等三角形的性质;熟练掌握全等三角形的对应角相等的性质是解决问题的关键.
【考点】坐标确定位置.
【分析】根据平面直角坐标系写出博物馆的坐标即可.
解:由图可知,博物馆的坐标为(2,2).
故选D.
【点评】本题考查了坐标确定位置,熟练掌握平面直角坐标系中点的坐标的写法是解题的关键.
【考点】 三角形的重心; 等腰直角三角形.
【分析】连接CP并延长,交AB于D,根据重心的性质得到CD是△ABC的中线,PD=CD,根据直角三角形的性质求出CD,计算即可.
解:连接CP并延长,交AB于D,
∵P是Rt△ABC的重心,
∴CD是△ABC的中线,PD=CD,
∵∠C=90°,
∴CD=AB=3,
∵AC=BC,CD是△ABC的中线,
∴CD⊥AB,
∴PD=1,即点P到AB所在直线的距离等于1,
故选:A.
【考点】作图—基本作图.
【分析】根据线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质判断即可.
解:A.由作图可知,AQ平分∠BAC,
∴∠BAP=∠CAP=∠BAC=40°,
故选项A正确,不符合题意,
B.由作图可知,MQ是BC的垂直平分线,
∴∠DEB=90°,
∵∠B=30°,
∴DE=BD,
故选项B正确,不符合题意,
C.∵∠B=30°,∠BAP=40°,
∴∠AFC=70°,
∵∠C=70°,
∴AF=AC,
故选项C正确,不符合题意,
D.∵∠EFQ=∠AFC=70°,∠QEF=90°,
∴∠EQF=20°,
故选项D错误,符合题意.
故选:D.
【点评】本题考查了线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质等知识,解题的关键是读懂图象信息.
【考点】平行线的性质,三角形内角和定理
【分析】先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠CED,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D.
解:∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,
∴∠D=75°.
故选:B.
【点评】此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.
【考点】全等三角形的性质.
【分析】由全等三角形的性质得出对应角相等∠C=∠AED=78°,即可得出结论.
解:∵△ABC≌△ADE,
∴∠C=∠AED=78°;
故选:D.
【点评】本题考查了全等三角形的性质;熟练掌握全等三角形的对应角相等的性质是解决问题的关键.
【考点】函数关系式;规律型:图形的变化类
【分析】根据图示可知,第一层是4个,第二层是8个,第三层是12,…第n层是4n,所以,即可确定y与n的关系.解:由图可知:
n=1时,圆点有4个,即y=4;
n=2时,圆点有8个,即y=8;
所以y=4n.
故选B.
【点评】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.解题关键是根据图形找到点的排列规律.
【考点】全等三角形的判定.
【分析】根据题目中的条件和全等三角形的判定方法,可以得到判定△ABO≌△DCO的依据.
解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
故选:B.
【点评】本题考查全等三角形的判定,解答本题的关键是明确题意,写出△AOB和△DOC全等的证明过程.
【考点】点的坐标特征
【分析】根据第一象限点的横坐标是正数判断出a、b同号,再根据非负数的性质和各象限内点的坐标特征解答.
解:∵点A(,1)在第一象限,
∴>0,
∴a、b同号,
∴-a2<0,ab>0,
∴点B(-a2,ab)在第二象限.
故答案为:B.
【点评】本题考查了各象限内点的坐标的符号特征,解题关键是记住各象限内点的坐标的符号.
【考点】函数的图象.
【分析】分别求出甲乙两人到达C地的时间,再结合已知条件即可解决问题.
解;由题意,甲走了1小时到了B地,在B地休息了半个小时,2小时正好走到C地,乙走了小时到了C地,在C地休息了小时.
由此可知正确的图象是A.
故选A.
【点评】本题考查函数图象、路程.速度、时间之间的关系,解题的关键是理解题意,读懂图象信息解决问题,属于中考常考题型.
【考点】线段垂直平分线的性质,轴对称-最短路线问题
【分析】由基本作图得到得EF垂直平分AB,则MB=MA,所以BM+MD=MA+MD,连接MA.DA,如图,利用两点之间线段最短可判断MA+MD的最小值为AD,再利用等腰三角形的性质得到AD⊥BC,然后利用三角形面积公式计算出AD即可.
解:由作法得EF垂直平分AB,
∴MB=MA,
∴BM+MD=MA+MD,
连接MA.DA,如图,
∵MA+MD≥AD(当且仅当M点在AD上时取等号),
∴MA+MD的最小值为AD,
∵AB=AC,D点为BC的中点,
∴AD⊥BC,
∵
∴
∴BM+MD长度的最小值为5.
故选:D.
【点评】本题考查的是线段的垂直平分线的性质,利用轴对称求线段和的最小值,三角形的面积,两点之间,线段最短,掌握以上知识是解题的关键.
1 、填空题
【考点】关于原点对称的点的坐标.
【分析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),即求关于原点的对称点时,横、纵坐标都变成原数的相反数.
解:根据两个点关于原点对称,则横、纵坐标都是原数的相反数,
得m﹣2=﹣5,
∴m=﹣3.
故答案为:﹣3.
【点评】本题主要考查了平面直角坐标系内两点关于原点的对称点时,横、纵坐标都变成原数的相反数,难度适中.
【考点】三角形的外角性质.
【分析】由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A,然后利用角平分线的定义计算即可.
解:∵∠ACD=∠B+∠A,
而∠A=80°,∠B=4°,
∴∠ACD=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=60°,
故答案为60
【点评】本题考查了三角形的外角定理,关键是根据三角形任意一个外角等于与之不相邻的两内角的和.
【考点】一次函数与一元一次不等式.
【分析】根据函数图象中的数据和一次函数的性质,可以写出等式kx+b>3的解集.
解:由图象可得,
当x=﹣1时,y=3,该函数y随x的增大而减小,
∴不等式kx+b>3的解集为x<﹣1,
故答案为:x<﹣1.
【点评】本题考查一次函数与一元一次不等式,解答本题的关键是明确一次函数与一元一次不等式的关系,利用数形结合的思想解答.
【考点】全等三角形的判定
【分析】根据角边角可证得,即可.
解:可添加∠A=∠D,理由如下:
∵,
∴∠DCE=∠ACB,
∵,∠A=∠D,
∴.
故答案为:∠A=∠D(答案不唯一)
【点评】本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
【考点】一次函数图象上点的坐标特征,规律型:点的坐标.
【分析】根据每条直线与x轴交点的横坐标解答即可.
解:由题知,这组直线是平行直线,每条直线与x轴交点的横坐标依次是2,4,6...,
∴第5条直线与x轴的交点的横坐标是10.
故答案为:10.
【点评】本题考查了一次函数图象上点的坐标特征,掌握一次函数图象上点的坐标特征是解题的关键.
【考点】翻折变换(折叠问题),等腰三角形的性质.
【分析】分两种情况,一是点B′在直线BC的下方,则∠BDB′=90°,所以∠ADB′=∠ADB=135°,则∠BAD=180°﹣∠B﹣∠ADB=25°,二是点B′在直线BC的上方,则∠ADB′=∠ADB=45°,所以∠BAD=180°﹣∠B﹣∠ADB=115°,于是得到问题的答案.
解:当点B′在直线BC的下方,如图1,
∵B′D⊥BC,
∴∠BDB′=90°,
∴∠ADB′+∠ADB=360°﹣90°=270°,
∵将三角形纸片沿AD对折,使点B落在点B′处,
∴∠ADB′=∠ADB=×270°=135°,
∵∠B=20°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣20°﹣135°=25°,
当点B′在直线BC的上方时,如图2,
∵B′D⊥BC,
∴∠BDB′=90°,
∵将三角形纸片沿AD对折,使点B落在点B′处,
∴∠ADB′=∠ADB=×90°=45°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣20°﹣45°=115°,
故答案为:25°或115°.
【点评】此题重点考查等腰三角形的性质、轴对称的性质、三角形内角和定理等知识,正确地求出∠BAB′的度数是解题的关键.
1 、解答题
【考点】三角形三边关系;绝对值
【分析】三角形三边满足的条件是:两边和大于第三边,两边的差小于第三边,根据此条件来确定绝对值内的式子的正负,从而化简计算即可.
解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,则a+b﹣c>0,a﹣b﹣c<0,a+b+c>0,
∴|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|=a+b﹣c+2a﹣2b﹣2c+a+b+c=4a﹣2c.
【点评】此题考查了三角形三边关系,此题的关键是先根据三角形三边的关系来判定绝对值内式子的正负.
【考点】正方形的性质,全等三角形的判定与性质
【分析】利用正方形的性质证明:AB=BC=CD,∠ABE=∠BCF=90°,再证明BE=CF,可得三角形的全等,利用全等三角形的性质可得答案.
证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°,
又∵CE=DF,
∴CE+BC=DF+CD即BE=CF,
在△BCF和△ABE中,
∴(SAS),
∴AE=BF.
【点评】本题考查的是正方形的性质,三角形全等的判定与性质,掌握以上知识是解题的关键.
【考点】坐标与图形性质;三角形的面积.
【分析】(1)直接根据三角形面积公式求解;
(2)设C(0,t),根据三角形面积公式得到 |t﹣3| 2=6,然后解绝对值方程求出t即可得到C点坐标.
解:(1)如图:
S△AOB=×2×3=3;
(2)设C(0,t),
∵三角形ABC的面积为6,
∴ |t﹣3| 2=6,
解得t=9或﹣3.
∴C点坐标为(0,﹣3),(0,9).
【点评】本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了三角形面积公式.
【考点】作图—复杂作图.
【分析】(1)利用基本作图(过一点作已知直线的垂线)作出垂线段CD即可;
(2)利用基本作图(过一点作已知直线的垂线)作出垂线段BE即可;
(3)利用基本作图(过一个角的平分线)作出CF即可;
(4)利用基本作图(作线段的垂直平分线)作出BC的垂直平分线得到BC的中点,则AM为所作.
解:(1)如图,CD为所作;
(2)如图,BE为所作;
(3)如图,CF为所作;
(4)如图,AM为所作.
【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
【考点】分式方程的应用,一次函数的应用
【分析】(1)设每盒水银体温计的价格是x元,根据用1200元购买口罩盒数与用300元购买水银体温计的盒数相同列出方程,求解即可;
(2)先用m表示出需要水银体温计的支数,再表示出水银体温计的盒数;
(3)分当m≤4时,当m>4时,分别得出关系式,再合并,根据若该校九年级有900名学生求出口罩的盒数m,从而得到体温计的盒数以及总费用.
解:(1)设每盒水银体温计的价格是x元,则每盒口罩的价格是x+150元,
根据题意可得:,
解得:x=50,
经检验:x=50是原方程的解,
50+150=200元,
∴每盒口罩和每盒水银体温计的价格各是200元,50元;
(2)∵购买口罩m盒,
∴共有口罩100m个,
∵给每位学生发放2只口罩和1支水银体温计,
∴需要发放支水银体温计,
∴需要购买盒水银体温计;
(3)由题意可得:
令200m+5m×50=1800,
解得:m=4,
若未超过1800元,即当m≤4时,
则w=200m+5m×50=450m,
若超过1800元,即当m>4时,
w=(200m+5m×50-1800)×0.8+1800=360m+360,
∴w关于m的函数关系式为,
若该校九年级有900名学生,即=900,
解得:m=18,
则=6840,
答:需要购买口罩18盒,水银体温计90盒,所需总费用为6840元.
【点评】本题考查了分式方程的实际应用,一次函数的实际应用,解题的关键是理解题意,弄清口罩盒数与体温计盒数的配套关系.
【考点】二元一次方程组的应用;一元一次不等式组的应用;一次函数的应用
【分析】(1)根据“2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元”,建立方程组即可得出结论;
(2)根据题意建立函数关系式,由A型桌椅不少于120套,B型桌椅不少于70套,确定出x的范围;
(3)根据一次函数的性质,即可得出结论.
解:(1)设A型桌椅的单价为a元,B型桌椅的单价为b元,
根据题意知,,
解得,,
即:A,B两型桌椅的单价分别为600元,800元;
(2)根据题意知,y=600x+800(200﹣x)+200×10=﹣200x+162000(120≤x≤130),
(3)由(2)知,y=﹣200x+162000(120≤x≤130),
∴当x=130时,总费用最少,
即:购买A型桌椅130套,购买B型桌椅70套,总费用最少,最少费用为136000元.
【点评】本题考查一次函数的应用,二元一次方程的应用,一元一次不等式组的应用,读懂题意,列出方程组或不等式是解本题的关键.
【考点】坐标与图形性质;三角形的面积.
【分析】(1)根据点的平移规律易得点C,D的坐标;
(2)先计算出S平行四边形ABOC=8,设M坐标为(0,m),根据三角形面积公式得×4×|m|=8,解得m=±4,于是可得M点的坐标为(0,4)或(0,﹣4);
(3)①先计算出S梯形OCDB=7,再讨论:当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP<4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;
②分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO﹣∠EPC=∠BOP﹣∠DCP,于是∠BOP﹣∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
解:(1)由平移可知:C(0,2),D(4,2);
(2)∵AB=4,CO=2,
∴S平行四边形ABOC=AB CO=4×2=8,
设M坐标为(0,m),
∴×4×|m|=8,解得m=±4
∴M点的坐标为(0,4)或(0,﹣4);
(3)①S梯形OCDB=×(3+4)×2=7,
当点P运动到点B时,S△BOC最小,S△BOC的最小值=×3×2=3,S△CDP+S△BOP<4,
当点P运动到点D时,S△BOC最大,S△BOC的最大值=×4×2=4,S△CDP+S△BOP>3,
所以3<S△CDP+S△BOP<4;
②当点P在BD上,如图1,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠EPO﹣∠EPC=∠BOP﹣∠DCP,
∴∠BOP﹣∠DCP=∠CPO;
同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
【点评】 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查三角形面积公式和平行线的性质.
【考点】 等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30角的直角三角形的性质
【分析】 (1)由等腰三角形的性质和已知条件得出∠BAD=∠DAC=×120°=60°,再证出∠ADE=∠ADF=90°﹣60°=30°,由含30角的直角三角形的性质得出AE=AD,AF=AD,即可得出结论;
(2)连接BD,证明△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠ABD=∠DAC,得出∠EDB=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF,即可得出结论.
(1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=∠BAC,
∵∠BAC=120°,
∴∠BAD=∠DAC=×120°=60°,
∵DE⊥AB,DF⊥AC,
∴∠ADE=∠ADF=90°﹣60°=30°,
∴AE=AD,AF=AD,
∴AE+AF=AD+AD=AD;
(2)解:线段AE,AF,AD之间的数量关系为:AE+AF=AD,理由如下:
连接BD,如图所示:
∵∠BAD=60°,AB=AD,
∴△ABD是等边三角形,
∴BD=AD,∠ABD=∠ADB=60°,
∵∠DAC=60°,
∴∠ABD=∠DAC,
∵∠EDB+∠EDA=∠EDA+∠ADF=60°,
∴∠EDB=∠ADF,
在△BDE与△ADF中,,
∴△BDE≌△ADF(ASA),
∴BE=AF,
∵AE+BE=AD,
∴AE+AF=AD.
【点评】本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30角的直角三角形的性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
