2.4二次函数的应用第1课时(同步课件)-2023-2024学年九年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 2.4二次函数的应用第1课时(同步课件)-2023-2024学年九年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:07:29 | ||
图片预览



文档简介
(共27张PPT)
北师大版 数学 九年级下册
第1课时
第二章 二次函数
4 二次函数的应用
学习目标
1.分析实际问题中变量之间的二次函数关系.(难点)
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.(重点)
复习回顾
用待定系数法求二次函数表达式的常见设法:
(1)一般式:y=ax2+bx+c;(已知抛物线上三点坐标或三对x、y的值,用一般式)
(2)顶点式:y=a(x-h)2+k;(已知抛物线的顶点坐标或对称轴或最值,用顶点式)
(3)交点式:y=a(x-x1)(x-x2).(已知抛物线与x轴交点的横坐标x1,x2,用交点式)
一、创设情境,引入新知
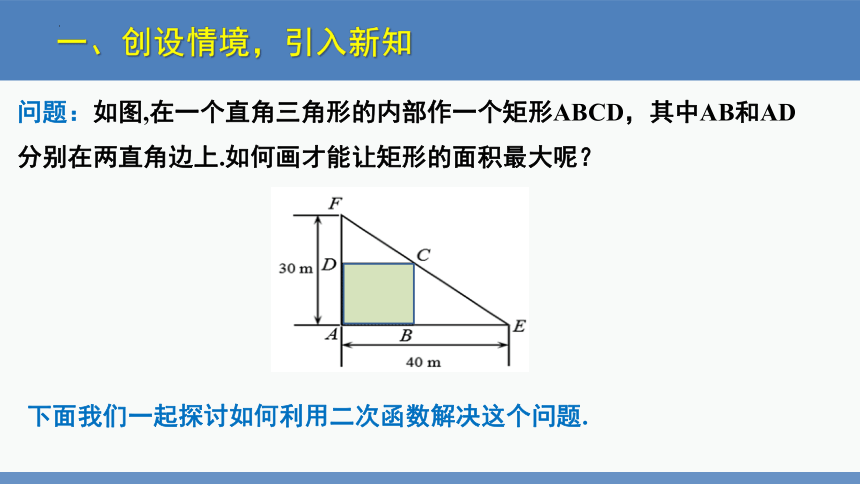
问题:如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.如何画才能让矩形的面积最大呢?
下面我们一起探讨如何利用二次函数解决这个问题.
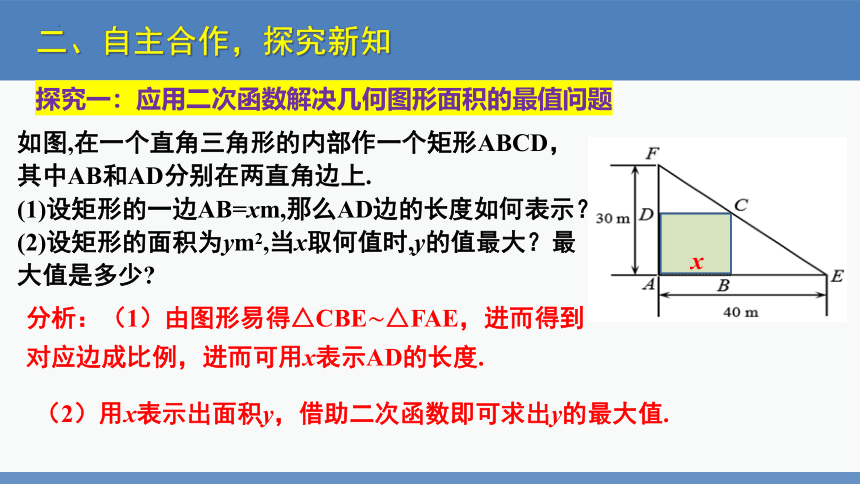
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少
二、自主合作,探究新知
探究一:应用二次函数解决几何图形面积的最值问题
(2)用x表示出面积y,借助二次函数即可求出y的最大值.
分析:(1)由图形易得△CBE△FAE,进而得到对应边成比例,进而可用x表示AD的长度.
x
二、自主合作,探究新知
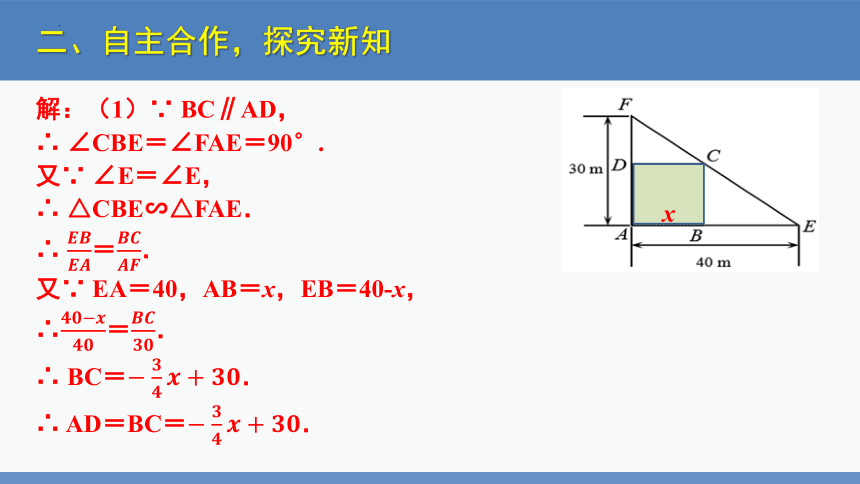
解:(1)∵ BC∥AD,
∴ ∠CBE=∠FAE=90°.
又∵ ∠E=∠E,
∴ △CBE∽△FAE.
∴ =.
又∵ EA=40,AB=x,EB=40-x,
∴=.
∴ BC=.
∴ AD=BC=.
x
二、自主合作,探究新知
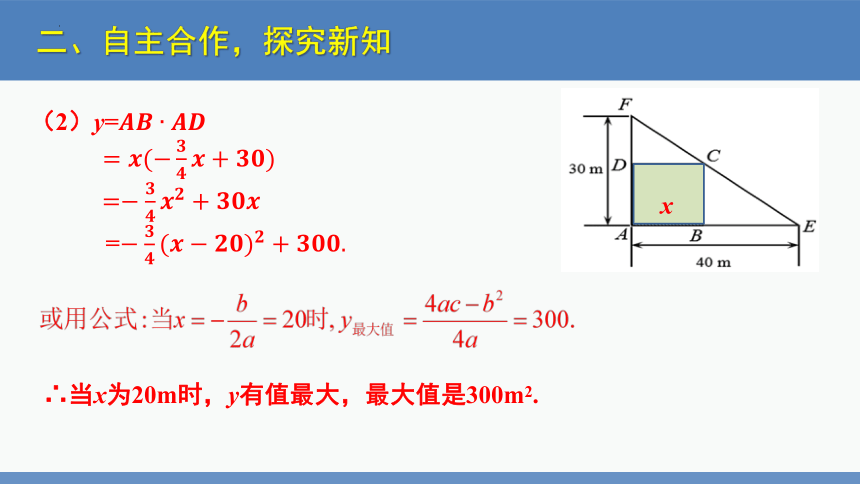
(2)y=
=
∴当x为20m时,y有值最大,最大值是300m2.
x
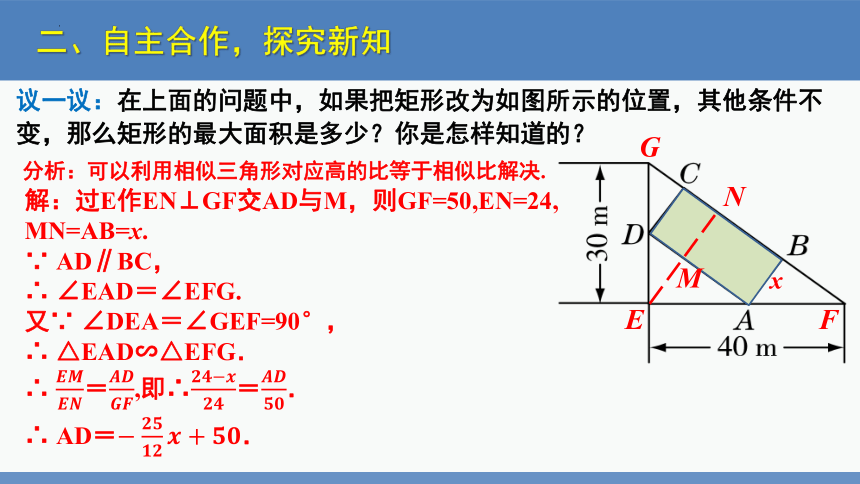
议一议:在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
二、自主合作,探究新知
分析:可以利用相似三角形对应高的比等于相似比解决.
x
F
G
E
N
M
解:过E作EN⊥GF交AD与M,则GF=50,EN=24,
MN=AB=x.
∵ AD∥BC,
∴ ∠EAD=∠EFG.
又∵ ∠DEA=∠GEF=90°,
∴ △EAD∽△EFG.
∴ =,即∴=.
∴ AD=.
二、自主合作,探究新知
x
F
G
E
N
M
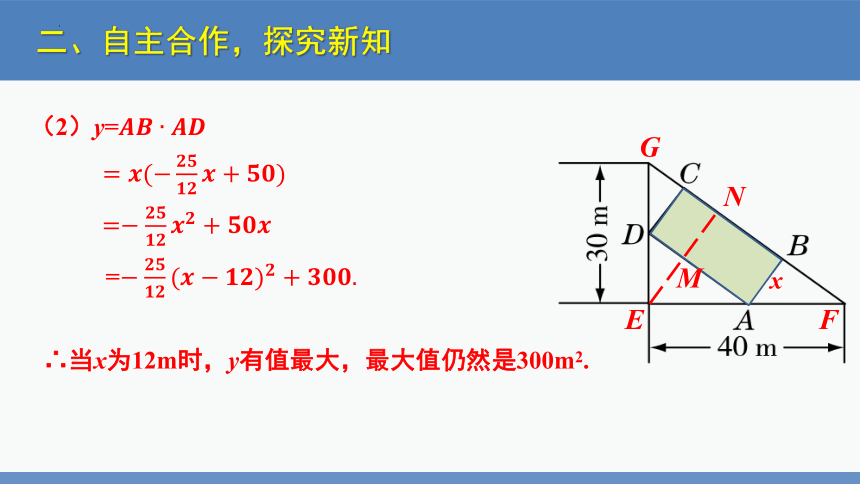
(2)y=
=
∴当x为12m时,y有值最大,最大值仍然是300m2.
知识要点
二、自主合作,探究新知
二次函数解决几何面积最值问题的方法
1.分析问题中的变量和常量,以及它们之间的关系;
2.求出函数解析式和自变量的取值范围;
3.配方变形,或利用公式求它的最大值或最小值,
4.检验结果的合理性:检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
二、自主合作,探究新知
典型例题
例1:某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m) 此时,窗户的面积是多少
解:∵7x+4y+πx=15,
∴0<x<1.48.
二、自主合作,探究新知
设窗户的面积是S m2, 则
∴当x约为1.07m时,窗户通过的光线最多.此时,窗户的面积约为4.02 m2.
做一做:要使运动员坐着船从圣火的拱形桥下穿过入场,现知拱形底座顶部离水面2 m,水面宽4 m,为了船能顺利通过,需要把水面下降1 m,问此时水面宽度增加多少
二、自主合作,探究新知
探究二:应用二次函数解决拱桥问题
x
y
O
-3
(-2,-2) ●
● (2,-2)
4米
二、自主合作,探究新知
解:建立如图所示坐标系,设二次函数解析式为y=ax2.
∵抛物线经过点(2,-2),
∴-2=4a,解得
∴这条抛物线的解析式为y=x2.
-3
x
y
O
(-2,-2) ●
● (2,-2)
当水面下降1m时,水面的纵坐标为y=-3.
当y=-3时,.
∴水面下降1m,水面的宽度为m.
∴水面的宽度增加了()m.
二、自主合作,探究新知
解决拱桥问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
知识要点
例2:如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8 m,宽AB为2 m,以BC所在直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6 m.(1)求抛物线的解析式.(2)如果该隧道内设双行道,现有一辆卡车高4.2 m,
宽2.4 m,这辆卡车能否通过该隧道?说明理由.
二、自主合作,探究新知
【分析】要求抛物线的解析式,需根据函数图象特点,设出顶点式进行求解.要判断这辆卡车能否通过该隧道,即求当x=2.4时,该抛物线的函数值是否大于4.2.
典型例题
二、自主合作,探究新知
解:(1)由题意,得E(0,6),D(4,2).
∵ 点E为顶点,
∴ 可设抛物线的解析式为y=ax2+6.
将点D的坐标代入,得16a+6=2,
解得a=-.
∴ y=-x2+6.
(2)这辆卡车能通过该隧道.理由如下:
∵ 当x=2.4时,y=-×2.42+6=4.56>4.2,
∴ 这辆卡车能通过该隧道.
1.某中学计划用20 m的围栏靠墙围成一个如图所示的矩形花园ABCD,设AB=x m,矩形的面积为S m ,S的最大值是( )A.20 m B.30 m C.40 m D.50 m
2.用长为8m的铝合金制成的形状为矩形的窗框,则窗框的透光面积最大为
( )
A. m2 B. m2 C.m2 D.4 m2
三、即学即练,应用知识
D
D
4.如图所示,一边靠墙(墙足够长),用120 m篱笆围成两间相等的矩形鸡舍,要使鸡舍的总面积最大,则每间鸡舍的长与宽分别是 m, m.
三、即学即练,应用知识
3.周长为16 cm的矩形的最大面积为 cm2.
16
30
20
5.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1 m宽的门.已知计划中的材料可建墙体(不包括门)总长为27 m,则能建成的饲养室面积最大为 m2.
75
6.一块三角形废料如图所示,∠C=90°,AC=8,BC=6.用这块废料剪出一个矩形CDEF,其中,点D,E,F分别在AC,AB,BC上.当AE为多长时所剪出的矩形CDEF面积最大 最大面积是多少
三、即学即练,应用知识
解:∵∠C=90°, AC=8, BC=6,
∴AB=10.
∵四边形CDEF是矩形,
∴EF∥AC,
∴△BEF∽△BAC,
∴
三、即学即练,应用知识
同理可得DE=x.
矩形CDEF的面积S=DE·EF
= = (0∴当x=5时, S有最大值,为12.
即当AE为5时, 所剪出的矩形CDEF面积最大, 最大面积为12.
设AE=x,则BE=10-x,
∴
∴EF=
四、课堂小结
建立函数关系式
常见几何图形的面积公式
依 据
一个关键
一个注意
最值有时不在顶点处,则要利用函数的增减性来确定.
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化的关键
建立恰当的直角坐标系
几何面积最值问题
拱桥问题
二次函数的应用
1.赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为,当水面离桥拱顶的高度DO是2m时,这时水面宽度AB为( )
A.-10m B. -5m C. 5m D. 10m
五、当堂达标检测
D
3.如图,在△ABC中, ∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始沿BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过
s,四边形APQC的面积最小.
A
B
C
P
Q
2.如图所示,用长8m的铝合金条制成如图的矩形窗框,那么最大的透光面积是 .
五、当堂达标检测
3
4. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
五、当堂达标检测
解:(1)因为矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0<x<6.
(2)S=-x2+6x=-(x-3)2+9;
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元)
五、当堂达标检测
5.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.(1)若花园的面积为192m2,求x的值;(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
解:(1)∵ AB=x m,∴ BC=(28-x)m,∴ x(28-x)=192,
解得x1=12,x2=16.
(2)由题意可得S=x(28-x)=-x2+28x=-(x-14)2+196.
∵ 在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,
∴ 当28-x=15,即x=13时,S取到最大值为-(13-14)2+196=195.
教材习题2.8;
六、布置作业
北师大版 数学 九年级下册
第1课时
第二章 二次函数
4 二次函数的应用
学习目标
1.分析实际问题中变量之间的二次函数关系.(难点)
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.(重点)
复习回顾
用待定系数法求二次函数表达式的常见设法:
(1)一般式:y=ax2+bx+c;(已知抛物线上三点坐标或三对x、y的值,用一般式)
(2)顶点式:y=a(x-h)2+k;(已知抛物线的顶点坐标或对称轴或最值,用顶点式)
(3)交点式:y=a(x-x1)(x-x2).(已知抛物线与x轴交点的横坐标x1,x2,用交点式)
一、创设情境,引入新知
问题:如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.如何画才能让矩形的面积最大呢?
下面我们一起探讨如何利用二次函数解决这个问题.
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少
二、自主合作,探究新知
探究一:应用二次函数解决几何图形面积的最值问题
(2)用x表示出面积y,借助二次函数即可求出y的最大值.
分析:(1)由图形易得△CBE△FAE,进而得到对应边成比例,进而可用x表示AD的长度.
x
二、自主合作,探究新知
解:(1)∵ BC∥AD,
∴ ∠CBE=∠FAE=90°.
又∵ ∠E=∠E,
∴ △CBE∽△FAE.
∴ =.
又∵ EA=40,AB=x,EB=40-x,
∴=.
∴ BC=.
∴ AD=BC=.
x
二、自主合作,探究新知
(2)y=
=
∴当x为20m时,y有值最大,最大值是300m2.
x
议一议:在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
二、自主合作,探究新知
分析:可以利用相似三角形对应高的比等于相似比解决.
x
F
G
E
N
M
解:过E作EN⊥GF交AD与M,则GF=50,EN=24,
MN=AB=x.
∵ AD∥BC,
∴ ∠EAD=∠EFG.
又∵ ∠DEA=∠GEF=90°,
∴ △EAD∽△EFG.
∴ =,即∴=.
∴ AD=.
二、自主合作,探究新知
x
F
G
E
N
M
(2)y=
=
∴当x为12m时,y有值最大,最大值仍然是300m2.
知识要点
二、自主合作,探究新知
二次函数解决几何面积最值问题的方法
1.分析问题中的变量和常量,以及它们之间的关系;
2.求出函数解析式和自变量的取值范围;
3.配方变形,或利用公式求它的最大值或最小值,
4.检验结果的合理性:检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
二、自主合作,探究新知
典型例题
例1:某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m) 此时,窗户的面积是多少
解:∵7x+4y+πx=15,
∴0<x<1.48.
二、自主合作,探究新知
设窗户的面积是S m2, 则
∴当x约为1.07m时,窗户通过的光线最多.此时,窗户的面积约为4.02 m2.
做一做:要使运动员坐着船从圣火的拱形桥下穿过入场,现知拱形底座顶部离水面2 m,水面宽4 m,为了船能顺利通过,需要把水面下降1 m,问此时水面宽度增加多少
二、自主合作,探究新知
探究二:应用二次函数解决拱桥问题
x
y
O
-3
(-2,-2) ●
● (2,-2)
4米
二、自主合作,探究新知
解:建立如图所示坐标系,设二次函数解析式为y=ax2.
∵抛物线经过点(2,-2),
∴-2=4a,解得
∴这条抛物线的解析式为y=x2.
-3
x
y
O
(-2,-2) ●
● (2,-2)
当水面下降1m时,水面的纵坐标为y=-3.
当y=-3时,.
∴水面下降1m,水面的宽度为m.
∴水面的宽度增加了()m.
二、自主合作,探究新知
解决拱桥问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
知识要点
例2:如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8 m,宽AB为2 m,以BC所在直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6 m.(1)求抛物线的解析式.(2)如果该隧道内设双行道,现有一辆卡车高4.2 m,
宽2.4 m,这辆卡车能否通过该隧道?说明理由.
二、自主合作,探究新知
【分析】要求抛物线的解析式,需根据函数图象特点,设出顶点式进行求解.要判断这辆卡车能否通过该隧道,即求当x=2.4时,该抛物线的函数值是否大于4.2.
典型例题
二、自主合作,探究新知
解:(1)由题意,得E(0,6),D(4,2).
∵ 点E为顶点,
∴ 可设抛物线的解析式为y=ax2+6.
将点D的坐标代入,得16a+6=2,
解得a=-.
∴ y=-x2+6.
(2)这辆卡车能通过该隧道.理由如下:
∵ 当x=2.4时,y=-×2.42+6=4.56>4.2,
∴ 这辆卡车能通过该隧道.
1.某中学计划用20 m的围栏靠墙围成一个如图所示的矩形花园ABCD,设AB=x m,矩形的面积为S m ,S的最大值是( )A.20 m B.30 m C.40 m D.50 m
2.用长为8m的铝合金制成的形状为矩形的窗框,则窗框的透光面积最大为
( )
A. m2 B. m2 C.m2 D.4 m2
三、即学即练,应用知识
D
D
4.如图所示,一边靠墙(墙足够长),用120 m篱笆围成两间相等的矩形鸡舍,要使鸡舍的总面积最大,则每间鸡舍的长与宽分别是 m, m.
三、即学即练,应用知识
3.周长为16 cm的矩形的最大面积为 cm2.
16
30
20
5.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1 m宽的门.已知计划中的材料可建墙体(不包括门)总长为27 m,则能建成的饲养室面积最大为 m2.
75
6.一块三角形废料如图所示,∠C=90°,AC=8,BC=6.用这块废料剪出一个矩形CDEF,其中,点D,E,F分别在AC,AB,BC上.当AE为多长时所剪出的矩形CDEF面积最大 最大面积是多少
三、即学即练,应用知识
解:∵∠C=90°, AC=8, BC=6,
∴AB=10.
∵四边形CDEF是矩形,
∴EF∥AC,
∴△BEF∽△BAC,
∴
三、即学即练,应用知识
同理可得DE=x.
矩形CDEF的面积S=DE·EF
= = (0
即当AE为5时, 所剪出的矩形CDEF面积最大, 最大面积为12.
设AE=x,则BE=10-x,
∴
∴EF=
四、课堂小结
建立函数关系式
常见几何图形的面积公式
依 据
一个关键
一个注意
最值有时不在顶点处,则要利用函数的增减性来确定.
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化的关键
建立恰当的直角坐标系
几何面积最值问题
拱桥问题
二次函数的应用
1.赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为,当水面离桥拱顶的高度DO是2m时,这时水面宽度AB为( )
A.-10m B. -5m C. 5m D. 10m
五、当堂达标检测
D
3.如图,在△ABC中, ∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始沿BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过
s,四边形APQC的面积最小.
A
B
C
P
Q
2.如图所示,用长8m的铝合金条制成如图的矩形窗框,那么最大的透光面积是 .
五、当堂达标检测
3
4. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
五、当堂达标检测
解:(1)因为矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0<x<6.
(2)S=-x2+6x=-(x-3)2+9;
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元)
五、当堂达标检测
5.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.(1)若花园的面积为192m2,求x的值;(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
解:(1)∵ AB=x m,∴ BC=(28-x)m,∴ x(28-x)=192,
解得x1=12,x2=16.
(2)由题意可得S=x(28-x)=-x2+28x=-(x-14)2+196.
∵ 在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,
∴ 当28-x=15,即x=13时,S取到最大值为-(13-14)2+196=195.
教材习题2.8;
六、布置作业
