2.5二次函数与一元二次方程第1课时(同步课件)-2023-2024学年九年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 2.5二次函数与一元二次方程第1课时(同步课件)-2023-2024学年九年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:19:58 | ||
图片预览





文档简介
(共28张PPT)
北师大版 数学 九年级下册
第1课时
第二章 二次函数
5 二次函数与一元二次方程
学习目标
1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系.(重点)
3.理解一元二次方程的根就是二次函数与x轴交点的横坐标.(难点)
1.一元二次方程a+bx+c=0的根的判别式Δ= ,
当Δ_____0时,方程有两个不相等的实数根;
当________时,有两个相等的实数根;
当________时,没有实数根.
复习回顾
>
Δ=0
Δ<0
2.一次函数y=kx+b的图象与x轴的交点的 就是一元一次方程kx+b=0的根.
横坐标
一、创设情境,引入新知
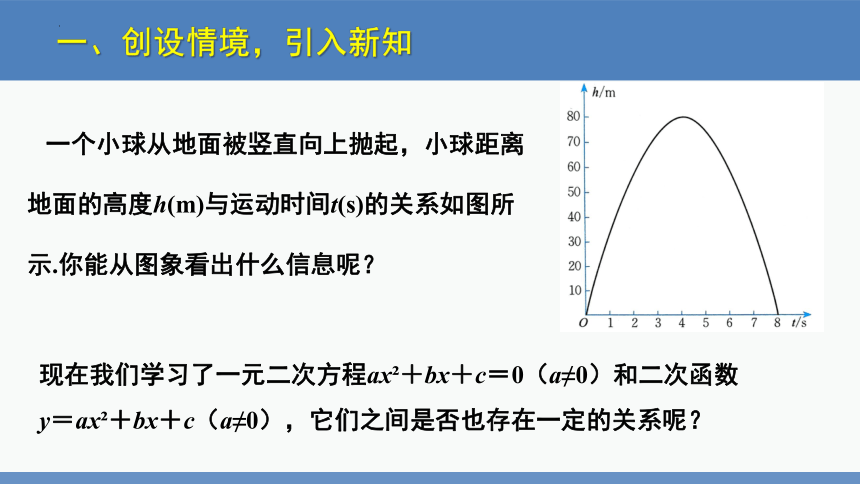
现在我们学习了一元二次方程ax +bx+c=0(a≠0)和二次函数y=ax +bx+c(a≠0),它们之间是否也存在一定的关系呢?
一个小球从地面被竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示.你能从图象看出什么信息呢?
二、自主合作,探究新知
探究:二次函数与一元二次方程的关系
我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可以近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面被以40 m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示,那么
(1)h与t的关系式是什么?
解:(1)由图象可得h0=0,v0=40.
∴h与t的关系式为h=-5t2+40t.
二、自主合作,探究新知
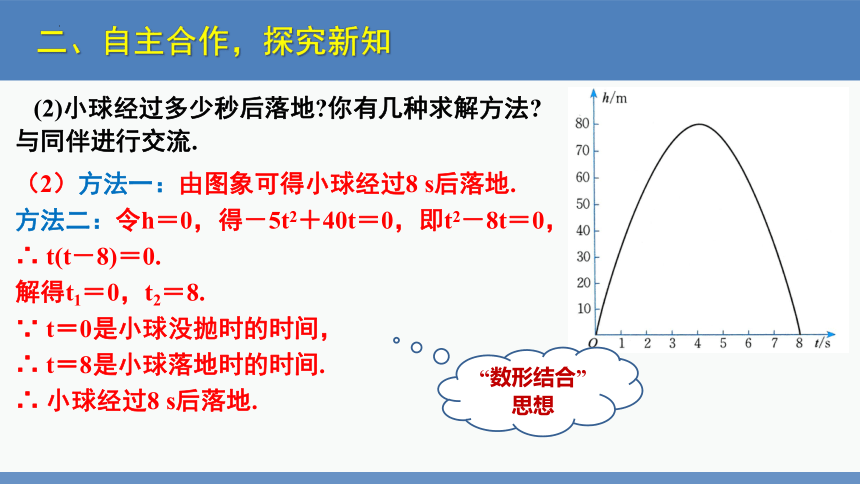
(2)方法一:由图象可得小球经过8 s后落地.
方法二:令h=0,得-5t2+40t=0,即t2-8t=0,
∴ t(t-8)=0.
解得t1=0,t2=8.
∵ t=0是小球没抛时的时间,
∴ t=8是小球落地时的时间.
∴ 小球经过8 s后落地.
“数形结合”思想
(2)小球经过多少秒后落地 你有几种求解方法 与同伴进行交流.
二、自主合作,探究新知
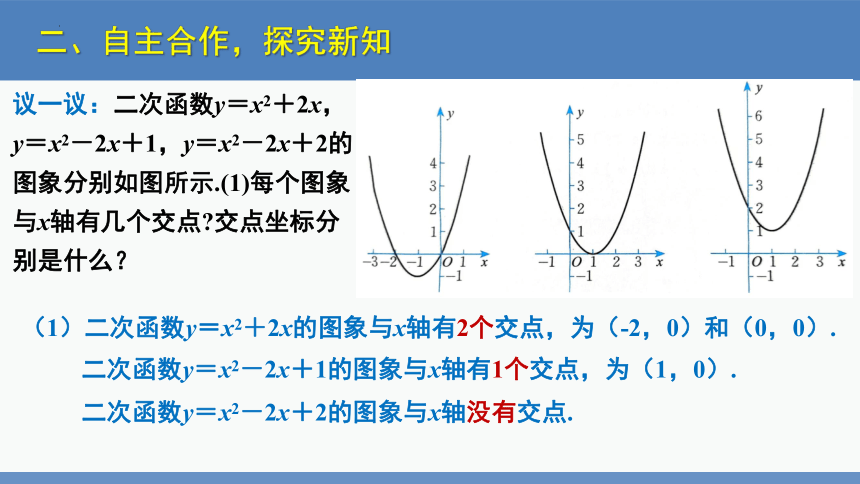
议一议:二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象分别如图所示.(1)每个图象与x轴有几个交点 交点坐标分别是什么?
(1)二次函数y=x2+2x的图象与x轴有2个交点,为(-2,0)和(0,0).
二次函数y=x2-2x+1的图象与x轴有1个交点,为(1,0).
二次函数y=x2-2x+2的图象与x轴没有交点.
二、自主合作,探究新知
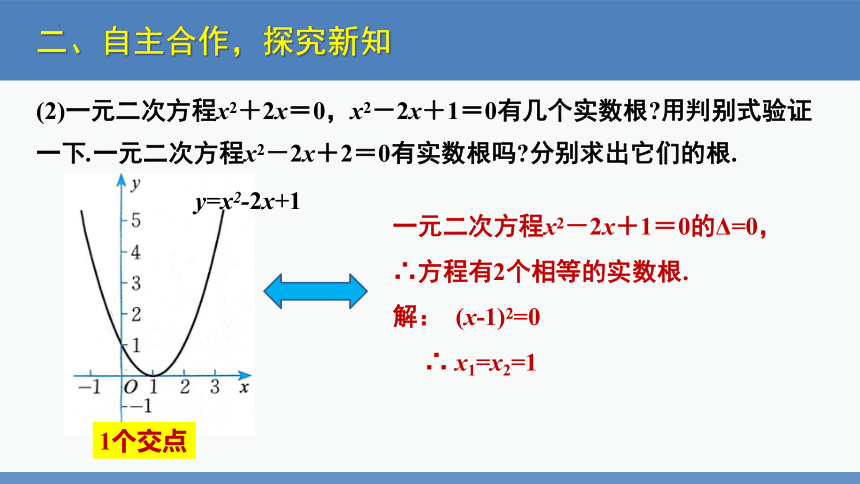
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程x2-2x+2=0有实数根吗 分别求出它们的根.
一元二次方程x2+2x=0的Δ=4>0,
∴方程有2个不相等的实数根.
解:x(x+2)=0
x=0或x+2=0
∴ x1=-2,x2=0
y=x2+2x
2个交点
二、自主合作,探究新知
一元二次方程x2-2x+1=0的Δ=0,
∴方程有2个相等的实数根.
解: (x-1)2=0
∴ x1=x2=1
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程x2-2x+2=0有实数根吗 分别求出它们的根.
y=x2-2x+1
1个交点
二、自主合作,探究新知
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程x2-2x+2=0有实数根吗 分别求出它们的根.
∵一元二次方程x2-2x+2=0的Δ=-4<0,
∴方程没有实数根.
y=x2-2x+2
没有交点
二、自主合作,探究新知
(3)二次函数y=ax +bx+c的图象与x轴交点的横坐标和一元二次方程ax +bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系:
二次函数y=ax +bx+c的图象与x轴的交点有三种情况:有两个交点、有一个交点、没有交点.
与此相对应,一元二次方程ax2+bx+c=0的根也有三种情况:有两个不相等的实数根(b2-4ac>0)、有两个相等的实数根(b2-4ac=0)、没有实数根(b2-4ac<0).
二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
二、自主合作,探究新知
典型例题
分析:求二次函数的图象与x轴的交点坐标,只需令y=0,求出x的值即可.
【方法总结】一元二次方程ax2+bx+c=0的根即为二次函数y=ax2+bx+c的图象与x轴的交点的横坐标.
例1:求二次函数y=-(x-2)2+1的图象与x轴的交点坐标.
解:令y=-(x-2)2+1=0,
解得x1=0,x2=4.
∴ 二次函数y=-(x-2)2+1的图象与x轴的交点坐标为(0,0),(4,0).
二、自主合作,探究新知
例2: 已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有交点;
(1)证明:∵m≠0,
∴Δ=(m+2)2-4m×2=m2+4m+4-8m=(m-2)2.
∵(m-2)2≥0,
∴Δ≥0,
∴此抛物线与x轴总有交点;
典型例题
二、自主合作,探究新知
例2: 已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
(2)解:令y=0,则(x-1)(mx-2)=0,
所以 x-1=0或mx-2=0,
解得 x1=1,x2=.
当m为正整数1时,x2为整数且x1≠x2,即抛物线与x轴总有两个交点,且它们的横坐标都是整数.
所以正整数m的值为1.
典型例题
想一想:在本节一开始的小球上抛问题中,何时小球离地面的高度是60m?你是如何知道的?
二、自主合作,探究新知
方法一:令h=60,即-5t2+40t=60,
解得 t1=2,t2=6,
∴2s或6s时,小球离地面的高度是60m.
方法二:由图象可得.
【方法归纳】可以利用图象,也可以解方程.
二、自主合作,探究新知
x
y
o
2
4
1
练一练:一元二次方程的根与二次函数的图象有什么关系?试把方程的根在图象上表示出来.
一元二次方程的根即为二次函数当y值为1时,对应的x的值.
由图象得一元二次方程的根为x1=2,x2=4.
知识要点
二、自主合作,探究新知
一般地,当二次函数y=ax2+bx+c(a≠0)的y取某一定值m时,求自变量x的值,可以解一元二次方程ax2+bx+c=m.
反过来,解方程ax2+bx+c=m又可以看作已知二次函数y=ax2+bx+c(a≠0)的值为m,求自变量x的值.
二次函数与一元二次方程的关系:
例3:如图,某学生推铅球,铅球出手(点A处)的高度是0.6m,出手后的铅球沿一段抛物线运行,当运行到最高3m时,水平距离x=4m.
(1)求这个二次函数的解析式;
二、自主合作,探究新知
典型例题
解:(1)设二次函数的解析式为y=a(x-4)2+3,
把(0,0.6)代入得
0.6=a(0-4)2+3,解得
∴
二、自主合作,探究新知
(2)该同学把铅球推出去多远?
(2)当y=0时,0
解得(舍去).
答:该男同学把铅球推出去(4+2)m远.
三、即学即练,应用知识
1.抛物线y=-3x2-x+4与坐标轴的交点个数是( )A.3个 B.2个 C.1个 D.0个
2.小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )A.无解 B.x=1C.x=-4 D.x1=-1,x2=4
A
D
5.抛物线y=(k﹣1)﹣x+1与x轴有交点,则k的取值范围是 ______________ .
三、即学即练,应用知识
3.若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为___________.
-1
4.已知方程的两个根分别为,,那么可知抛物线与x轴的交点为 .
(-1,0)(3,0)
≤
三、即学即练,应用知识
6. 已知二次函数y=2x2-mx-m2.(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为(1,0),求B点坐标.
(1)证明:2x2-mx-m2=0,Δ=(-m)2-4×2×(-m2)=9m2.∵ m2≥0,∴ 9m2≥0,∴ 对于任意实数m,该二次函数图象与x轴总有公共点.
三、即学即练,应用知识
(2)解:把(1,0)代入二次函数表达式,得2-m-m2=0,∴ m1=-2,m2=1.当m=-2时,二次函数表达式为y=2x2+2x-4,令y=0,得2x2+2x-4=0,解得x=1或x=-2,∴ 二次函数图象与x轴的两个公共点的坐标是(1,0),(-2,0).又∵ A点坐标为(1,0),∴ B(-2,0).
当m=1时,同理可得B().
四、课堂小结
二次函数y=ax +bx+c(a≠0)的图象与x轴的位置关系 一元二次方程ax +bx+c=0(a≠0)的根的情况 b2-4ac的值
有两个公共点 有两个不相等的实数根 b2-4ac>0
只有一个公共点 有两个相等的实数根 b2-4ac=0
无公共点 无实数根 b2-4ac<0
1.二次函数与一元二次方程有下列对应关系:
2.抛物线y=ax2+bx+c与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
2.小兰画了一个函数的图像如图,则关于x的方程的解是( )
A.无解 B.
C. D.
x
y
o
-1
4
1.若一元二次方程有两个相等的实数根,则函数与x轴的交点个数为( )
A.有两个交点 B.有一个交点
C.没有交点 D.以上都不对
五、当堂达标检测
B
D
4.若关于x的函数与x轴仅有一个交点,则实数k的值为 .
3.抛物线与坐标轴的交点个数是( )
A.3个 B.2个 C.1个 D.0个
五、当堂达标检测
B
-1
5.抛物线y=2(x﹣1)(x﹣3)与x轴的交点坐标是 _________________.
(1,0),(3,0)
6.已知关于x的一元二次方程+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=+x﹣m的部分图象如图所示,求一元二次方程+x﹣m=0的解.
五、当堂达标检测
解:(1)∵一元二次方程+x﹣m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,
∴m>,
∴m的取值范围为m>;
(2)二次函数y=+x﹣m图象的对称轴为直线x,
∴抛物线与x轴两个交点关于直线x对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
教材习题2.10;
六、布置作业
北师大版 数学 九年级下册
第1课时
第二章 二次函数
5 二次函数与一元二次方程
学习目标
1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系.(重点)
3.理解一元二次方程的根就是二次函数与x轴交点的横坐标.(难点)
1.一元二次方程a+bx+c=0的根的判别式Δ= ,
当Δ_____0时,方程有两个不相等的实数根;
当________时,有两个相等的实数根;
当________时,没有实数根.
复习回顾
>
Δ=0
Δ<0
2.一次函数y=kx+b的图象与x轴的交点的 就是一元一次方程kx+b=0的根.
横坐标
一、创设情境,引入新知
现在我们学习了一元二次方程ax +bx+c=0(a≠0)和二次函数y=ax +bx+c(a≠0),它们之间是否也存在一定的关系呢?
一个小球从地面被竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示.你能从图象看出什么信息呢?
二、自主合作,探究新知
探究:二次函数与一元二次方程的关系
我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可以近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面被以40 m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示,那么
(1)h与t的关系式是什么?
解:(1)由图象可得h0=0,v0=40.
∴h与t的关系式为h=-5t2+40t.
二、自主合作,探究新知
(2)方法一:由图象可得小球经过8 s后落地.
方法二:令h=0,得-5t2+40t=0,即t2-8t=0,
∴ t(t-8)=0.
解得t1=0,t2=8.
∵ t=0是小球没抛时的时间,
∴ t=8是小球落地时的时间.
∴ 小球经过8 s后落地.
“数形结合”思想
(2)小球经过多少秒后落地 你有几种求解方法 与同伴进行交流.
二、自主合作,探究新知
议一议:二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象分别如图所示.(1)每个图象与x轴有几个交点 交点坐标分别是什么?
(1)二次函数y=x2+2x的图象与x轴有2个交点,为(-2,0)和(0,0).
二次函数y=x2-2x+1的图象与x轴有1个交点,为(1,0).
二次函数y=x2-2x+2的图象与x轴没有交点.
二、自主合作,探究新知
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程x2-2x+2=0有实数根吗 分别求出它们的根.
一元二次方程x2+2x=0的Δ=4>0,
∴方程有2个不相等的实数根.
解:x(x+2)=0
x=0或x+2=0
∴ x1=-2,x2=0
y=x2+2x
2个交点
二、自主合作,探究新知
一元二次方程x2-2x+1=0的Δ=0,
∴方程有2个相等的实数根.
解: (x-1)2=0
∴ x1=x2=1
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程x2-2x+2=0有实数根吗 分别求出它们的根.
y=x2-2x+1
1个交点
二、自主合作,探究新知
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根 用判别式验证一下.一元二次方程x2-2x+2=0有实数根吗 分别求出它们的根.
∵一元二次方程x2-2x+2=0的Δ=-4<0,
∴方程没有实数根.
y=x2-2x+2
没有交点
二、自主合作,探究新知
(3)二次函数y=ax +bx+c的图象与x轴交点的横坐标和一元二次方程ax +bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系:
二次函数y=ax +bx+c的图象与x轴的交点有三种情况:有两个交点、有一个交点、没有交点.
与此相对应,一元二次方程ax2+bx+c=0的根也有三种情况:有两个不相等的实数根(b2-4ac>0)、有两个相等的实数根(b2-4ac=0)、没有实数根(b2-4ac<0).
二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
二、自主合作,探究新知
典型例题
分析:求二次函数的图象与x轴的交点坐标,只需令y=0,求出x的值即可.
【方法总结】一元二次方程ax2+bx+c=0的根即为二次函数y=ax2+bx+c的图象与x轴的交点的横坐标.
例1:求二次函数y=-(x-2)2+1的图象与x轴的交点坐标.
解:令y=-(x-2)2+1=0,
解得x1=0,x2=4.
∴ 二次函数y=-(x-2)2+1的图象与x轴的交点坐标为(0,0),(4,0).
二、自主合作,探究新知
例2: 已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有交点;
(1)证明:∵m≠0,
∴Δ=(m+2)2-4m×2=m2+4m+4-8m=(m-2)2.
∵(m-2)2≥0,
∴Δ≥0,
∴此抛物线与x轴总有交点;
典型例题
二、自主合作,探究新知
例2: 已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
(2)解:令y=0,则(x-1)(mx-2)=0,
所以 x-1=0或mx-2=0,
解得 x1=1,x2=.
当m为正整数1时,x2为整数且x1≠x2,即抛物线与x轴总有两个交点,且它们的横坐标都是整数.
所以正整数m的值为1.
典型例题
想一想:在本节一开始的小球上抛问题中,何时小球离地面的高度是60m?你是如何知道的?
二、自主合作,探究新知
方法一:令h=60,即-5t2+40t=60,
解得 t1=2,t2=6,
∴2s或6s时,小球离地面的高度是60m.
方法二:由图象可得.
【方法归纳】可以利用图象,也可以解方程.
二、自主合作,探究新知
x
y
o
2
4
1
练一练:一元二次方程的根与二次函数的图象有什么关系?试把方程的根在图象上表示出来.
一元二次方程的根即为二次函数当y值为1时,对应的x的值.
由图象得一元二次方程的根为x1=2,x2=4.
知识要点
二、自主合作,探究新知
一般地,当二次函数y=ax2+bx+c(a≠0)的y取某一定值m时,求自变量x的值,可以解一元二次方程ax2+bx+c=m.
反过来,解方程ax2+bx+c=m又可以看作已知二次函数y=ax2+bx+c(a≠0)的值为m,求自变量x的值.
二次函数与一元二次方程的关系:
例3:如图,某学生推铅球,铅球出手(点A处)的高度是0.6m,出手后的铅球沿一段抛物线运行,当运行到最高3m时,水平距离x=4m.
(1)求这个二次函数的解析式;
二、自主合作,探究新知
典型例题
解:(1)设二次函数的解析式为y=a(x-4)2+3,
把(0,0.6)代入得
0.6=a(0-4)2+3,解得
∴
二、自主合作,探究新知
(2)该同学把铅球推出去多远?
(2)当y=0时,0
解得(舍去).
答:该男同学把铅球推出去(4+2)m远.
三、即学即练,应用知识
1.抛物线y=-3x2-x+4与坐标轴的交点个数是( )A.3个 B.2个 C.1个 D.0个
2.小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )A.无解 B.x=1C.x=-4 D.x1=-1,x2=4
A
D
5.抛物线y=(k﹣1)﹣x+1与x轴有交点,则k的取值范围是 ______________ .
三、即学即练,应用知识
3.若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为___________.
-1
4.已知方程的两个根分别为,,那么可知抛物线与x轴的交点为 .
(-1,0)(3,0)
≤
三、即学即练,应用知识
6. 已知二次函数y=2x2-mx-m2.(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为(1,0),求B点坐标.
(1)证明:2x2-mx-m2=0,Δ=(-m)2-4×2×(-m2)=9m2.∵ m2≥0,∴ 9m2≥0,∴ 对于任意实数m,该二次函数图象与x轴总有公共点.
三、即学即练,应用知识
(2)解:把(1,0)代入二次函数表达式,得2-m-m2=0,∴ m1=-2,m2=1.当m=-2时,二次函数表达式为y=2x2+2x-4,令y=0,得2x2+2x-4=0,解得x=1或x=-2,∴ 二次函数图象与x轴的两个公共点的坐标是(1,0),(-2,0).又∵ A点坐标为(1,0),∴ B(-2,0).
当m=1时,同理可得B().
四、课堂小结
二次函数y=ax +bx+c(a≠0)的图象与x轴的位置关系 一元二次方程ax +bx+c=0(a≠0)的根的情况 b2-4ac的值
有两个公共点 有两个不相等的实数根 b2-4ac>0
只有一个公共点 有两个相等的实数根 b2-4ac=0
无公共点 无实数根 b2-4ac<0
1.二次函数与一元二次方程有下列对应关系:
2.抛物线y=ax2+bx+c与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
2.小兰画了一个函数的图像如图,则关于x的方程的解是( )
A.无解 B.
C. D.
x
y
o
-1
4
1.若一元二次方程有两个相等的实数根,则函数与x轴的交点个数为( )
A.有两个交点 B.有一个交点
C.没有交点 D.以上都不对
五、当堂达标检测
B
D
4.若关于x的函数与x轴仅有一个交点,则实数k的值为 .
3.抛物线与坐标轴的交点个数是( )
A.3个 B.2个 C.1个 D.0个
五、当堂达标检测
B
-1
5.抛物线y=2(x﹣1)(x﹣3)与x轴的交点坐标是 _________________.
(1,0),(3,0)
6.已知关于x的一元二次方程+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=+x﹣m的部分图象如图所示,求一元二次方程+x﹣m=0的解.
五、当堂达标检测
解:(1)∵一元二次方程+x﹣m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,
∴m>,
∴m的取值范围为m>;
(2)二次函数y=+x﹣m图象的对称轴为直线x,
∴抛物线与x轴两个交点关于直线x对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
教材习题2.10;
六、布置作业
