3.1圆(同步课件)-2023-2024学年九年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 3.1圆(同步课件)-2023-2024学年九年级数学下册同步精品课堂(北师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:50:17 | ||
图片预览








文档简介
(共24张PPT)
北师大版 数学 九年级下册
第三章 圆
1 圆
学习目标
1.知道圆的有关定义及表示方法;(重点)
2.掌握点和圆的位置关系;(重点)
3.会根据要求画出图形.(难点)
一、创设情境,引入新知
与三角形、四边形一样,圆也是我们常见的图形.本章将运用我们以前学习过的对称、平移、旋转以及证明等方法研究圆的有关性质,并利用这些知识解决一些实际问题.
思考:车轮为什么做成圆形 你知道怎样利用直角尺检查某些工件恰好为半圆形吗?用一张三角形的纸片,你能裁出一个尽可能大的圆吗?
一、创设情境,引入新知
一些学生正在做投圈游戏,他们的投圈目标都是图中的花瓶.如果他们呈“一”字排开,这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形才公平?
二、自主合作,探究新知
探究一:圆的概念
·
r
O
A
前面我们已经认识了圆.观察画圆的过程,你能说出圆是如何画出来的吗?
圆的旋转定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“☉O”,读作“圆O”.
有关概念
固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
二、自主合作,探究新知
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
定长r
同一个圆上
问题:从画圆的过程可以看出什么呢?
圆可以看成是平面上到定点的距离等于定长的所有点组成的图形.定点就是圆心,定长就是半径.
圆的集合定义
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径(两者缺一不可).
二、自主合作,探究新知
典型例题
例1:矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
二、自主合作,探究新知
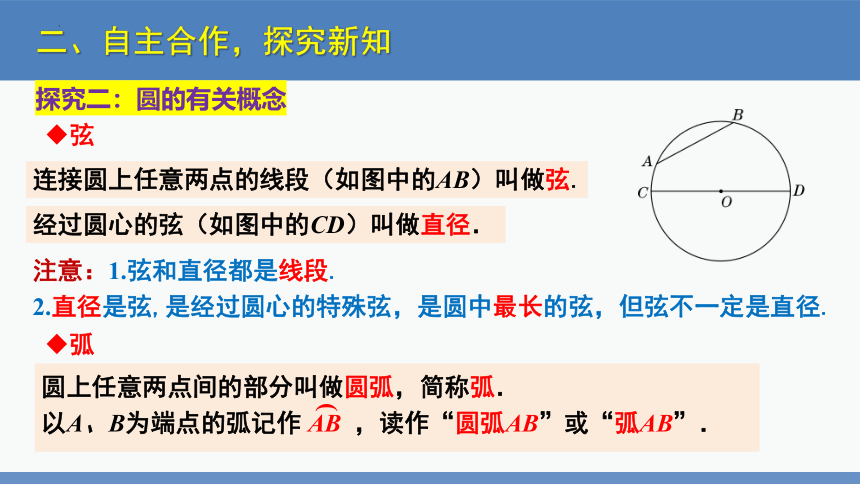
探究二:圆的有关概念
连接圆上任意两点的线段(如图中的AB)叫做弦.
经过圆心的弦(如图中的CD)叫做直径.
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
弦
弧
圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
二、自主合作,探究新知
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
劣弧与优弧
·
C
O
A
B
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
等圆与等弧
能够重合的两个圆叫做等圆.
在同圆或等圆中,能够互相重合的弧叫做等弧.
想一想:长度相等的弧是等弧吗?
例2:如图 (1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
(3)请任选一条弦,写出这条弦所对的弧.
A
B
C
E
F
D
O
二、自主合作,探究新知
弦AF,AB,AC.其中弦AB又是直径.
劣弧:
AF,
(
AD,
(
AC,
(
AE.
(
优弧:
AFE,
(
AFC,
(
AED,
(
AEF.
(
答案不唯一,如:弦AF,它所对的弧是 .
AF
(
典型例题
二、自主合作,探究新知
探究三:点和圆的位置关系
想一想:如图所示,☉O是一个半径为r的圆,在圆内、圆外、圆上分别取一点,点到圆心的距离为d,你能用r与d的大小关系刻画它们的位置特征吗?
点与圆的位置关系有三种:点在圆内,点在圆上,点在圆外.
思考:(1)在画图的过程中你认为点与圆有几种位置关系?
二、自主合作,探究新知
可以通过比较点到圆心的距离d和半径r的大小关系来确定.
思考:(2)怎样来确定点与圆的位置关系呢?
点在圆外,即d r;
点在圆上,即d r;
点在圆内,即d r.
>
=
<
反过来,已知点到圆心的距离与半径的关系也可以确定该点与圆的位置关系.
例3:圆心为O的两个同心圆,半径分别为1和2,若OP=,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
O
二、自主合作,探究新知
典型例题
D
知识要点
二、自主合作,探究新知
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在☉O内
d点P在☉O上
d=r
点P在☉O外
d>r
点P在圆环内
r<d<R
数形结合:
位置关系
数量关系
二、自主合作,探究新知
做一做:设AB=3cm,画图说明满足下列要求的图形:
(1)到点A和点B的距离都等于2cm的所有点组成的图形.
(2)到点A和点B的距离都小于2cm的所有点组成的图形.
解:(1)如图,分别以点A和B为圆心,2 cm为半径画☉A与☉B,两圆的交点C、D即为所求;
(2)如图,分别以点A和点B为圆心,2 cm为半径画☉A与☉B,两圆的重叠部分(不包括边线)即为所求.
【总结】满足条件的点一般以圆周为分界线,要分清是否包括边界.
2.设⊙O的半径为r,点P到圆心的距离d不大于r,则点P在( )
A.在⊙O内 B.在⊙O外
C.不在⊙O内 D.不在⊙O外
1.下列说法中,正确的是( )
A.弦是直径 B.半圆是弧
C.过圆心的线段是直径 D.圆心相同半径相同的两个圆是同心圆
三、即学即练,应用知识
3.A、B是半径为5的⊙O上两个不同的点,则弦AB的取值范围是( )A.AB>0 B.0<AB<5C.0<AB<10 D.0<AB≤10
B
D
D
三、即学即练,应用知识
4.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
5.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .
7cm或3cm
6.如图,在⊙O中,点A,O,D和点B,O,C分别在一条直线上,图中共有 条弦,它们分别是 .
3
AE,DC,AD
三、即学即练,应用知识
·
2cm
3cm
7.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
解:如图所示.
定义
有关概念
圆
点与圆的位置关系
四、课堂小结
旋转定义
集合定义
弦(直径)
弧
劣弧
半圆
优弧
要画一个确定的圆,关键是确定圆心和半径.
同圆半径相等
直径是圆中最长的弦
半圆是特殊的弧
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
五、当堂达标检测
1.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为 ( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.在⊙O上或⊙O外
B
2.圆内最长的弦长为10 cm,则圆的半径( ) A. 小于5 cm B. 大于5 cm C. 等于5 cm D. 不能确定
C
3.正方形ABCD的边长为2cm,以A为圆心,2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A .
五、当堂达标检测
上
外
上
直径
半径
一
二
四
四
4.填空:(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,
劣弧有 条.
A
B
C
D
O
F
E
5.一个点到已知圆上的点的最大距离是8,最小距离是2,则圆的半径是 .
5或3
6.如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
五、当堂达标检测
解:(1)AD=4=r,故D点在⊙A上,
AB=3AC=5>r,故C点在⊙A外.
五、当堂达标检测
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3教材习题3.1;
六、布置作业
北师大版 数学 九年级下册
第三章 圆
1 圆
学习目标
1.知道圆的有关定义及表示方法;(重点)
2.掌握点和圆的位置关系;(重点)
3.会根据要求画出图形.(难点)
一、创设情境,引入新知
与三角形、四边形一样,圆也是我们常见的图形.本章将运用我们以前学习过的对称、平移、旋转以及证明等方法研究圆的有关性质,并利用这些知识解决一些实际问题.
思考:车轮为什么做成圆形 你知道怎样利用直角尺检查某些工件恰好为半圆形吗?用一张三角形的纸片,你能裁出一个尽可能大的圆吗?
一、创设情境,引入新知
一些学生正在做投圈游戏,他们的投圈目标都是图中的花瓶.如果他们呈“一”字排开,这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形才公平?
二、自主合作,探究新知
探究一:圆的概念
·
r
O
A
前面我们已经认识了圆.观察画圆的过程,你能说出圆是如何画出来的吗?
圆的旋转定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“☉O”,读作“圆O”.
有关概念
固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
二、自主合作,探究新知
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
定长r
同一个圆上
问题:从画圆的过程可以看出什么呢?
圆可以看成是平面上到定点的距离等于定长的所有点组成的图形.定点就是圆心,定长就是半径.
圆的集合定义
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径(两者缺一不可).
二、自主合作,探究新知
典型例题
例1:矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
二、自主合作,探究新知
探究二:圆的有关概念
连接圆上任意两点的线段(如图中的AB)叫做弦.
经过圆心的弦(如图中的CD)叫做直径.
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
弦
弧
圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
二、自主合作,探究新知
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
劣弧与优弧
·
C
O
A
B
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
等圆与等弧
能够重合的两个圆叫做等圆.
在同圆或等圆中,能够互相重合的弧叫做等弧.
想一想:长度相等的弧是等弧吗?
例2:如图 (1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
(3)请任选一条弦,写出这条弦所对的弧.
A
B
C
E
F
D
O
二、自主合作,探究新知
弦AF,AB,AC.其中弦AB又是直径.
劣弧:
AF,
(
AD,
(
AC,
(
AE.
(
优弧:
AFE,
(
AFC,
(
AED,
(
AEF.
(
答案不唯一,如:弦AF,它所对的弧是 .
AF
(
典型例题
二、自主合作,探究新知
探究三:点和圆的位置关系
想一想:如图所示,☉O是一个半径为r的圆,在圆内、圆外、圆上分别取一点,点到圆心的距离为d,你能用r与d的大小关系刻画它们的位置特征吗?
点与圆的位置关系有三种:点在圆内,点在圆上,点在圆外.
思考:(1)在画图的过程中你认为点与圆有几种位置关系?
二、自主合作,探究新知
可以通过比较点到圆心的距离d和半径r的大小关系来确定.
思考:(2)怎样来确定点与圆的位置关系呢?
点在圆外,即d r;
点在圆上,即d r;
点在圆内,即d r.
>
=
<
反过来,已知点到圆心的距离与半径的关系也可以确定该点与圆的位置关系.
例3:圆心为O的两个同心圆,半径分别为1和2,若OP=,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
O
二、自主合作,探究新知
典型例题
D
知识要点
二、自主合作,探究新知
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在☉O内
d
d=r
点P在☉O外
d>r
点P在圆环内
r<d<R
数形结合:
位置关系
数量关系
二、自主合作,探究新知
做一做:设AB=3cm,画图说明满足下列要求的图形:
(1)到点A和点B的距离都等于2cm的所有点组成的图形.
(2)到点A和点B的距离都小于2cm的所有点组成的图形.
解:(1)如图,分别以点A和B为圆心,2 cm为半径画☉A与☉B,两圆的交点C、D即为所求;
(2)如图,分别以点A和点B为圆心,2 cm为半径画☉A与☉B,两圆的重叠部分(不包括边线)即为所求.
【总结】满足条件的点一般以圆周为分界线,要分清是否包括边界.
2.设⊙O的半径为r,点P到圆心的距离d不大于r,则点P在( )
A.在⊙O内 B.在⊙O外
C.不在⊙O内 D.不在⊙O外
1.下列说法中,正确的是( )
A.弦是直径 B.半圆是弧
C.过圆心的线段是直径 D.圆心相同半径相同的两个圆是同心圆
三、即学即练,应用知识
3.A、B是半径为5的⊙O上两个不同的点,则弦AB的取值范围是( )A.AB>0 B.0<AB<5C.0<AB<10 D.0<AB≤10
B
D
D
三、即学即练,应用知识
4.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
5.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .
7cm或3cm
6.如图,在⊙O中,点A,O,D和点B,O,C分别在一条直线上,图中共有 条弦,它们分别是 .
3
AE,DC,AD
三、即学即练,应用知识
·
2cm
3cm
7.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
解:如图所示.
定义
有关概念
圆
点与圆的位置关系
四、课堂小结
旋转定义
集合定义
弦(直径)
弧
劣弧
半圆
优弧
要画一个确定的圆,关键是确定圆心和半径.
同圆半径相等
直径是圆中最长的弦
半圆是特殊的弧
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
五、当堂达标检测
1.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为 ( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.在⊙O上或⊙O外
B
2.圆内最长的弦长为10 cm,则圆的半径( ) A. 小于5 cm B. 大于5 cm C. 等于5 cm D. 不能确定
C
3.正方形ABCD的边长为2cm,以A为圆心,2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A .
五、当堂达标检测
上
外
上
直径
半径
一
二
四
四
4.填空:(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,
劣弧有 条.
A
B
C
D
O
F
E
5.一个点到已知圆上的点的最大距离是8,最小距离是2,则圆的半径是 .
5或3
6.如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
五、当堂达标检测
解:(1)AD=4=r,故D点在⊙A上,
AB=3
五、当堂达标检测
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3
六、布置作业
