6.6 图形的位似(同步课件)-2023-2024学年九年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 6.6 图形的位似(同步课件)-2023-2024学年九年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:59:05 | ||
图片预览





文档简介
(共26张PPT)
6.6 图形的位似
第6章 图形的相似
教学目标
01
02
理解位似多边形的概念和性质、以及位似与相似的联系和区别
能利用位似原理将一个图形放大或缩小
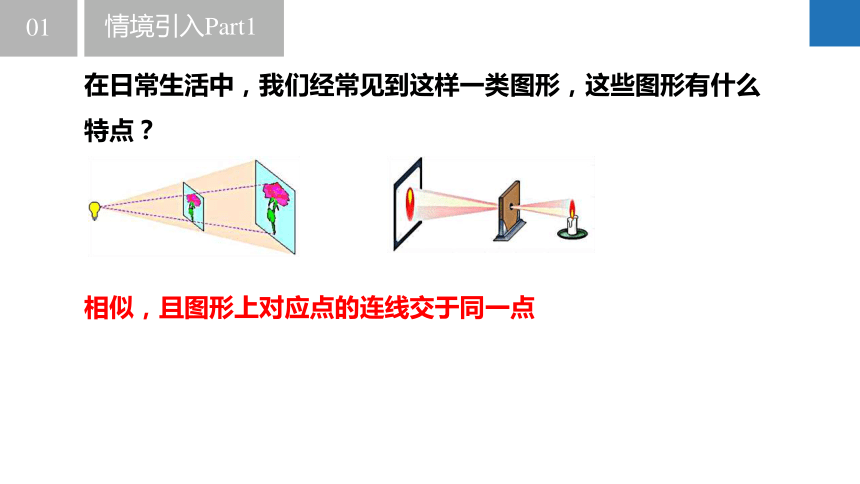
在日常生活中,我们经常见到这样一类图形,这些图形有什么特点?
相似,且图形上对应点的连线交于同一点
01
情境引入Part1
A
C
B
O
A’
B’
C’
01
情境引入Part2
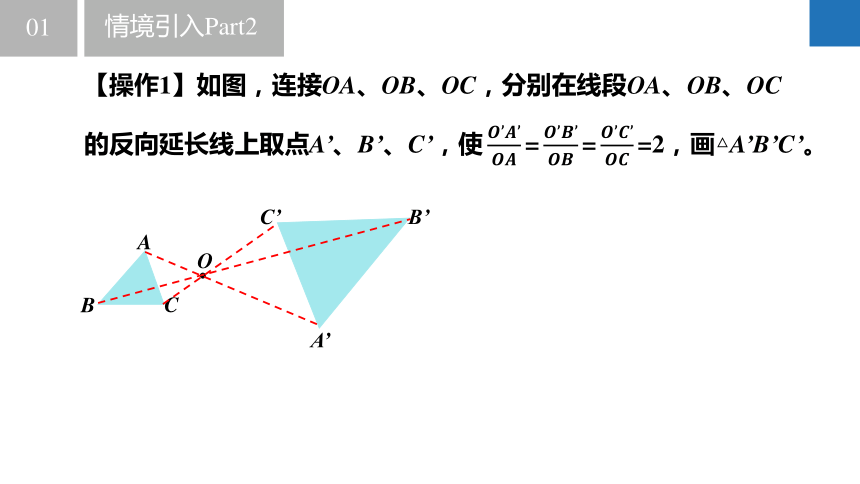
【操作1】如图,连接OA、OB、OC,分别在线段OA、OB、OC的反向延长线上取点A’、B’、C’,使===2,画△A’B’C’。
A
C
B
D
O
D’
C’
B’
A’
01
情境引入Part2
【操作2】如图,连接OC、OD,分别在线段OA、OB、OC、OD上取点A’、B’、C’、D’,使====;画△A’B’C’D’。
位似多边形
02
知识精讲
A
C
B
O
A’
B’
C’
A
C
B
D
O
D’
C’
B’
A’
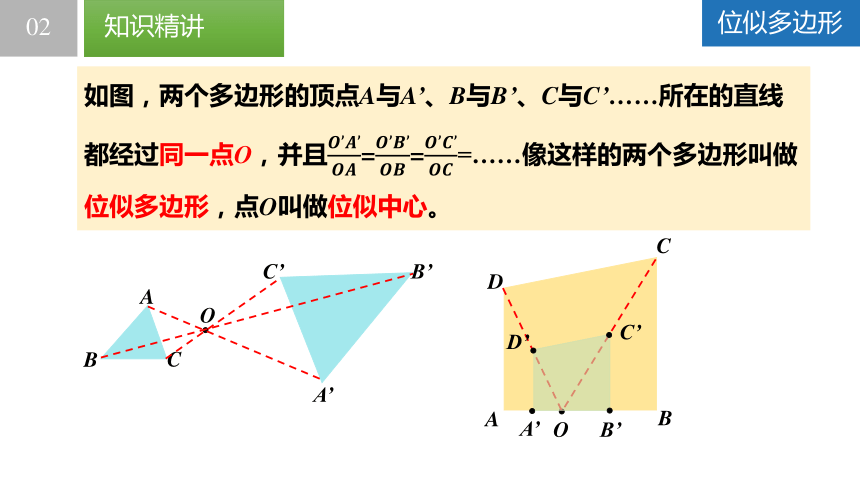
如图,两个多边形的顶点A与A’、B与B’、C与C’……所在的直线都经过同一点O,并且===……像这样的两个多边形叫做位似多边形,点O叫做位似中心。
位似多边形
02
知识精讲
定义解读:
∵两个位似多边形的顶点所在的直线都经过同一点(位似中心),
∴两个位似多边形的位似中心有且只有一个。
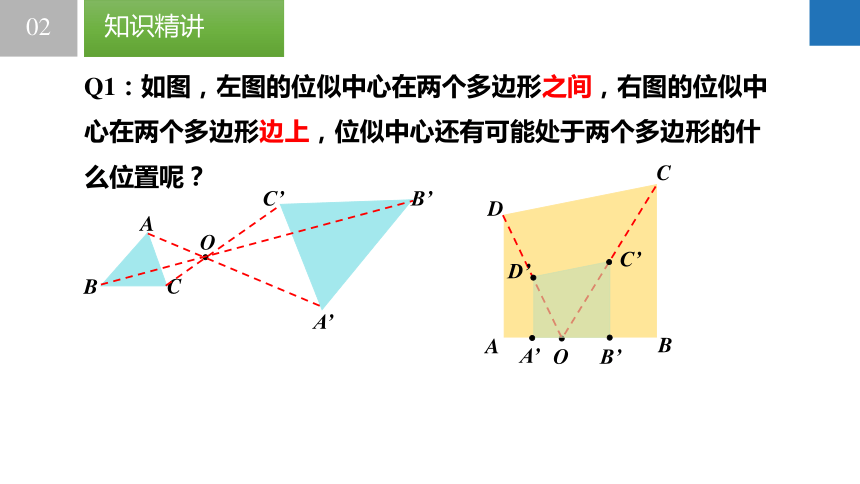
Q1:如图,左图的位似中心在两个多边形之间,右图的位似中心在两个多边形边上,位似中心还有可能处于两个多边形的什么位置呢?
02
知识精讲
A
C
B
O
A’
B’
C’
A
C
B
D
O
D’
C’
B’
A’
位似多边形
02
知识精讲
【总结】位似中心可能在两个多边形的之间或同侧,也可能位于两个多边形的边上(含顶点)或内部。
同侧
内部
顶点
Q2:根据位似多边形的概念,你能总结出位似多边形的哪些性质?
02
知识精讲
A
C
B
O
A’
B’
C’
A
C
B
D
O
D’
C’
B’
A’
(1)对应顶点所在的直线都经过同一点(位似中心);
(2)任意一组对应顶点到位似中心的距离之比都相等。
Q3-1:如图,△ABC与△A’B’C’是位似形,这两个三角形相似吗?
02
知识精讲
A
C
B
O
A’
B’
C’
【分析】∵△ABC与△A’B’C’是位似形,
∴===k,
又∵∠A’OB’=∠AOB,
∴△A’OB’∽△AOB,∴===k,
同理可得:===k,===k,
即=====,∴△A’B’C’∽△ABC。
Q3-2:如图,四边形ABCD与四边形A’B’C’D’是位似形,这两个四边形相似吗?
02
知识精讲
【分析】
∵四边形ABCD与四边形A’B’C’D’是位似形,
∴====k,∴==k,
又∵∠A’OD’=∠AOD,
∴△A’OD’∽△AOD,∴===k,
A
C
B
D
O
D’
C’
B’
A’
Q3-2:如图,四边形ABCD与四边形A’B’C’D’是位似形,这两个四边形相似吗?
02
知识精讲
A
C
B
D
O
D’
C’
B’
A’
同理可得:===k,===k,
即=======,
∴四边形A’B’C’D’∽四边形ABCD。
【总结】若两个多边形位似,则这两个多边形相似。
02
知识精讲
通过上述分析过程,你还能得到什么结论?
【总结】
若两个多边形位似,则这两个多边形任意一组对应顶点到位似中心的距离之比都等于相似比。
Q4-1:如图,△ABC与△A’B’C’是位似形,它们的对应边有怎样的位置关系。
【分析】
∵△A’OB’∽△AOB,
∴∠OA’B’=∠OAB,∴A’B’∥AB,
同理可得:B’C’∥BC,C’A’∥CA。
02
知识精讲
A
C
B
O
A’
B’
C’
Q4-2:如图,四边形ABCD与四边形A’B’C’D’是位似形,它们的对应边有怎样的位置关系?
02
知识精讲
A
C
B
D
O
D’
C’
B’
A’
【分析】
如图,A’B’和AB在同一条直线上,
∵△A’OD’∽△AOD,
∴∠OA’D’=∠OAD,∴D’A’∥DA,
同理可得:B’C’∥BC,C’D’∥CD。
02
知识精讲
【总结】若两个多边形位似,则这两个多边形对应边互相平行(或在同一条直线上)。
【分析】∵相似仅要求两个图形形状相同,
而位似还要求在相似的基础上对应顶点所在的直线都经过同一点(位似中心),
∴位似图形一定相似,但相似图形不一定位似。
Q5:相似图形一定位似吗?
如图,△ADE∽△ACB,但不位似。
02
知识精讲
相似
位似
02
知识精讲
【总结】相似与位似的关系:
(1)位似图形一定相似,但相似图形不一定位似;
(2)两个位似图形的位似比即相似比。
位似多边形的性质
02
知识精讲
两个位似多边形的性质:
(1)对应顶点所在的直线都经过同一点(位似中心);
(2)相似;
(3)任意一组对应顶点到位似中心的距离之比都等于相似比;
(4)对应边互相平行(或在同一条直线上)。
知识精讲
例1、下列各选项中的两个图形不是位似图形的是( )
A. B.
C. D.
D
03
典例精析
知识精讲
例2、如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为( )
A.(-4,0) B.(-3,0) C.(-2,0) D.(-1.5,0)
C
03
典例精析
【分析】∵点B的坐标为(2,4),点E的坐标为(-1,2),
∴AB=4,OA=2,OD=2,
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,
∴===,
∴PO=PA=OA=2,即P点坐标为(-2,0)。
知识精讲
例3、如图,以点O为位似中心,作四边形ABCD的位似图形A'B'C′D',已知OA:AA′=1:2,若四边形ABCD的周长是2,则四边形A'B'C′D'的周长是( )
A.4 B.6 C.16 D.18
B
03
典例精析
【分析】∵OA:AA′=1:2,∴OA:OA′=1:3,
∵四边形ABCD与四边形A'B'C′D'是位似图形,
∴==,
∴四边形ABCD的周长:四边形A'B'C′D'的周长=1:3,
∵四边形ABCD的周长是2,∴四边形A'B'C′D'的周长为6。
知识精讲
例4、如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB扩大为原来的4倍,则点A的对应点的坐标是( )
A.(,1)
B.(-,-1)
C.(8,16)或(-16,-8)
D.(8,16)或(-8,-16)
03
典例精析
D
【分析】注意两解
知识精讲
例5、如图,在边长为1个单位长度的小正方形网格中,
(1)画出△ABC向上平移6个单位,再向右平移5个单位后的△A1B1C1;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)直接写出△CC1C2的面积,及A1,A2的坐标。
03
典例精析
【分析】
(3)△CC1C2的面积=×3×6=9;
A1的坐标为(7,9);A2的坐标为(3,5)。
A1
B1
C1
A2
C2
课后总结
如图,两个多边形的顶点A与A’、B与B’、C与C’……所在的直线都经过同一点O,并且===……像这样的两个多边形叫做位似多边形,点O叫做位似中心。
两个位似多边形的性质:
(1)对应顶点所在的直线都经过同一点(位似中心);
(2)一定相似;
(3)任意一组对应顶点到位似中心的距离之比都等于相似比;
(4)对应边互相平行(或在同一条直线上)。
6.6 图形的位似
第6章 图形的相似
教学目标
01
02
理解位似多边形的概念和性质、以及位似与相似的联系和区别
能利用位似原理将一个图形放大或缩小
在日常生活中,我们经常见到这样一类图形,这些图形有什么特点?
相似,且图形上对应点的连线交于同一点
01
情境引入Part1
A
C
B
O
A’
B’
C’
01
情境引入Part2
【操作1】如图,连接OA、OB、OC,分别在线段OA、OB、OC的反向延长线上取点A’、B’、C’,使===2,画△A’B’C’。
A
C
B
D
O
D’
C’
B’
A’
01
情境引入Part2
【操作2】如图,连接OC、OD,分别在线段OA、OB、OC、OD上取点A’、B’、C’、D’,使====;画△A’B’C’D’。
位似多边形
02
知识精讲
A
C
B
O
A’
B’
C’
A
C
B
D
O
D’
C’
B’
A’
如图,两个多边形的顶点A与A’、B与B’、C与C’……所在的直线都经过同一点O,并且===……像这样的两个多边形叫做位似多边形,点O叫做位似中心。
位似多边形
02
知识精讲
定义解读:
∵两个位似多边形的顶点所在的直线都经过同一点(位似中心),
∴两个位似多边形的位似中心有且只有一个。
Q1:如图,左图的位似中心在两个多边形之间,右图的位似中心在两个多边形边上,位似中心还有可能处于两个多边形的什么位置呢?
02
知识精讲
A
C
B
O
A’
B’
C’
A
C
B
D
O
D’
C’
B’
A’
位似多边形
02
知识精讲
【总结】位似中心可能在两个多边形的之间或同侧,也可能位于两个多边形的边上(含顶点)或内部。
同侧
内部
顶点
Q2:根据位似多边形的概念,你能总结出位似多边形的哪些性质?
02
知识精讲
A
C
B
O
A’
B’
C’
A
C
B
D
O
D’
C’
B’
A’
(1)对应顶点所在的直线都经过同一点(位似中心);
(2)任意一组对应顶点到位似中心的距离之比都相等。
Q3-1:如图,△ABC与△A’B’C’是位似形,这两个三角形相似吗?
02
知识精讲
A
C
B
O
A’
B’
C’
【分析】∵△ABC与△A’B’C’是位似形,
∴===k,
又∵∠A’OB’=∠AOB,
∴△A’OB’∽△AOB,∴===k,
同理可得:===k,===k,
即=====,∴△A’B’C’∽△ABC。
Q3-2:如图,四边形ABCD与四边形A’B’C’D’是位似形,这两个四边形相似吗?
02
知识精讲
【分析】
∵四边形ABCD与四边形A’B’C’D’是位似形,
∴====k,∴==k,
又∵∠A’OD’=∠AOD,
∴△A’OD’∽△AOD,∴===k,
A
C
B
D
O
D’
C’
B’
A’
Q3-2:如图,四边形ABCD与四边形A’B’C’D’是位似形,这两个四边形相似吗?
02
知识精讲
A
C
B
D
O
D’
C’
B’
A’
同理可得:===k,===k,
即=======,
∴四边形A’B’C’D’∽四边形ABCD。
【总结】若两个多边形位似,则这两个多边形相似。
02
知识精讲
通过上述分析过程,你还能得到什么结论?
【总结】
若两个多边形位似,则这两个多边形任意一组对应顶点到位似中心的距离之比都等于相似比。
Q4-1:如图,△ABC与△A’B’C’是位似形,它们的对应边有怎样的位置关系。
【分析】
∵△A’OB’∽△AOB,
∴∠OA’B’=∠OAB,∴A’B’∥AB,
同理可得:B’C’∥BC,C’A’∥CA。
02
知识精讲
A
C
B
O
A’
B’
C’
Q4-2:如图,四边形ABCD与四边形A’B’C’D’是位似形,它们的对应边有怎样的位置关系?
02
知识精讲
A
C
B
D
O
D’
C’
B’
A’
【分析】
如图,A’B’和AB在同一条直线上,
∵△A’OD’∽△AOD,
∴∠OA’D’=∠OAD,∴D’A’∥DA,
同理可得:B’C’∥BC,C’D’∥CD。
02
知识精讲
【总结】若两个多边形位似,则这两个多边形对应边互相平行(或在同一条直线上)。
【分析】∵相似仅要求两个图形形状相同,
而位似还要求在相似的基础上对应顶点所在的直线都经过同一点(位似中心),
∴位似图形一定相似,但相似图形不一定位似。
Q5:相似图形一定位似吗?
如图,△ADE∽△ACB,但不位似。
02
知识精讲
相似
位似
02
知识精讲
【总结】相似与位似的关系:
(1)位似图形一定相似,但相似图形不一定位似;
(2)两个位似图形的位似比即相似比。
位似多边形的性质
02
知识精讲
两个位似多边形的性质:
(1)对应顶点所在的直线都经过同一点(位似中心);
(2)相似;
(3)任意一组对应顶点到位似中心的距离之比都等于相似比;
(4)对应边互相平行(或在同一条直线上)。
知识精讲
例1、下列各选项中的两个图形不是位似图形的是( )
A. B.
C. D.
D
03
典例精析
知识精讲
例2、如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为( )
A.(-4,0) B.(-3,0) C.(-2,0) D.(-1.5,0)
C
03
典例精析
【分析】∵点B的坐标为(2,4),点E的坐标为(-1,2),
∴AB=4,OA=2,OD=2,
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,
∴===,
∴PO=PA=OA=2,即P点坐标为(-2,0)。
知识精讲
例3、如图,以点O为位似中心,作四边形ABCD的位似图形A'B'C′D',已知OA:AA′=1:2,若四边形ABCD的周长是2,则四边形A'B'C′D'的周长是( )
A.4 B.6 C.16 D.18
B
03
典例精析
【分析】∵OA:AA′=1:2,∴OA:OA′=1:3,
∵四边形ABCD与四边形A'B'C′D'是位似图形,
∴==,
∴四边形ABCD的周长:四边形A'B'C′D'的周长=1:3,
∵四边形ABCD的周长是2,∴四边形A'B'C′D'的周长为6。
知识精讲
例4、如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB扩大为原来的4倍,则点A的对应点的坐标是( )
A.(,1)
B.(-,-1)
C.(8,16)或(-16,-8)
D.(8,16)或(-8,-16)
03
典例精析
D
【分析】注意两解
知识精讲
例5、如图,在边长为1个单位长度的小正方形网格中,
(1)画出△ABC向上平移6个单位,再向右平移5个单位后的△A1B1C1;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)直接写出△CC1C2的面积,及A1,A2的坐标。
03
典例精析
【分析】
(3)△CC1C2的面积=×3×6=9;
A1的坐标为(7,9);A2的坐标为(3,5)。
A1
B1
C1
A2
C2
课后总结
如图,两个多边形的顶点A与A’、B与B’、C与C’……所在的直线都经过同一点O,并且===……像这样的两个多边形叫做位似多边形,点O叫做位似中心。
两个位似多边形的性质:
(1)对应顶点所在的直线都经过同一点(位似中心);
(2)一定相似;
(3)任意一组对应顶点到位似中心的距离之比都等于相似比;
(4)对应边互相平行(或在同一条直线上)。
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
