6.7 用相似三角形解决问题(同步课件)-2023-2024学年九年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 6.7 用相似三角形解决问题(同步课件)-2023-2024学年九年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 41.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 10:04:52 | ||
图片预览










文档简介
(共36张PPT)
6.7 用相似三角形解决问题
第6章 图形的相似
教学目标
01
认识平行投影,并会根据平行投影画图;能利用平行投影下物高与影长的关系原理进行相关测量和计算
02
03
能通过对实际问题的研究,进一步建立“相似三角形”模型,从而解决问题
认识中心投影,并会根据中心投影画图;能利用中心投影下物高与影长的关系原理进行相关测量和计算
平行投影
光在空气中传播时,遇到不透明的物体,在这个物体后面光不能到达的区域便产生影。
01
情境引入
如图,在太阳光的照射下,树木、路灯、路标都产生了影。
通常,我们把太阳光看成平行光。
01
情境引入
平行投影
【拓展】平行投影分为:
正投影:如图(1),把投射线垂直于投影面的平行投影叫做正投影;
斜投影:如图(2),把投射线不垂直于投影面的平行投影叫做斜投影。
(1)
(2)
投射线
投射面
02
知识精讲
在平行光的照射下,物体所产生的影称为平行投影。
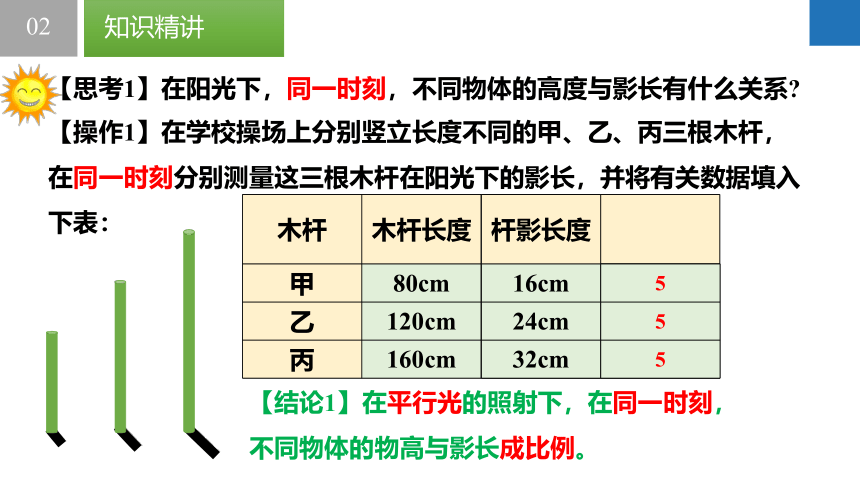
【思考1】在阳光下,同一时刻,不同物体的高度与影长有什么关系
【操作1】在学校操场上分别竖立长度不同的甲、乙、丙三根木杆,在同一时刻分别测量这三根木杆在阳光下的影长,并将有关数据填入下表:
【结论1】在平行光的照射下,在同一时刻,不同物体的物高与影长成比例。
木杆 木杆长度 杆影长度
甲 80cm
乙 120cm
丙 160cm
02
知识精讲
杆影长度
16cm
24cm
32cm
5
5
5
【思考2】在阳光下,不同时刻,同一物体的影长相等吗
02
知识精讲
【操作2】在不用时刻分别测量甲根木杆在阳光下的影长,并将有关数据填入下表:
【结论2】在平行光的照射下,在不同时刻,同一物体的影长不相等。
木杆 木杆长度 杆影长度
甲 80cm
80cm
80cm
杆影长度
16cm
40cm
80cm
02
知识精讲
平行投影
在平行光的照射下:
(1)在同一时刻,不同物体的物高与影长成比例;
(2)在不同时刻,同一物体的影长不相等。
练一练1-1:如图,甲木杆AB在阳光下的影长为BC,试在图中画出同一时刻乙、丙两根木杆在阳光下的影长。
甲
乙
丙
02
知识精讲
练一练1-2:如何运用“三角形的相似知识”来说明“平行光线的照射下,同一时刻物高与影长成比例”?
甲
乙
丙
A
B
C
D
E
F
02
知识精讲
【分析】建立如图所示的模型,
∵AC∥DF,
∴∠C=∠F,
∵∠B=∠E=90°,
∴△ABC∽△DEF,
∴=,即=。
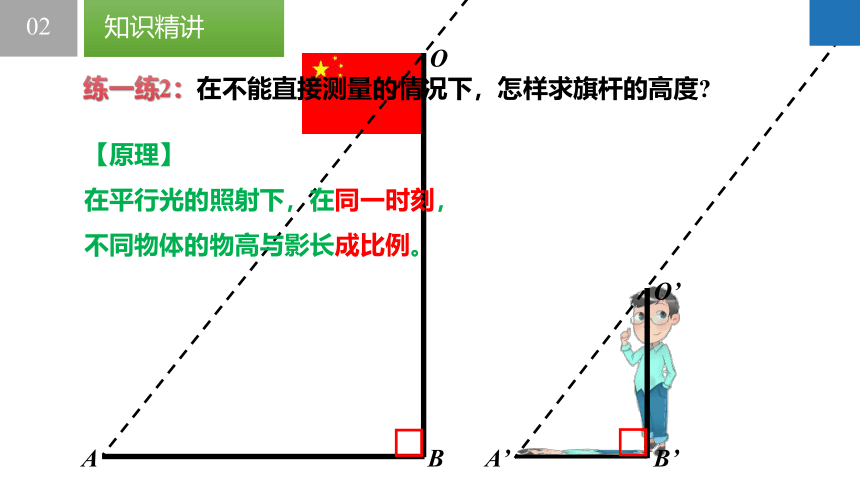
练一练2:在不能直接测量的情况下,怎样求旗杆的高度
A
B
O
A’
B’
O’
02
知识精讲
【原理】
在平行光的照射下,在同一时刻,
不同物体的物高与影长成比例。
【建模】如图,人的身高为O’B’=n,影长为A’B’=n,旗杆的影长为AB=m,求旗杆OB的高度。
02
知识精讲
【分析】
∵平行光,∴∠A=∠A’,
∵∠B=∠E=90°,∴△AOB∽△A’O’B’,
∴=,∴=,
∴=,即OB=。
02
知识精讲
【总结】
(1)=,即物高:参照物高=物影:参照物影;
(2)=,即物高:物影=参照物高:参照物影。
练一练3:古埃及国王曾请一位学者测量金字塔的高度。当这位学者确认在阳光下他的影长等于他的身高时(如图),要求他的助手同时测出金字塔的影长DB以及金字塔底部正方形的边长,这样他就知道了金字塔的高度。他是怎么算的呢?
02
知识精讲
【建模】如图,当学者的身高与影长相等时,测得金字塔的影长DB为32m,若金字塔底部正方形的边长为230m,你能帮助这位学者计算这座金字塔的高度吗?
02
知识精讲
【分析】
若无遮挡,AC对应的影长应为BC,
∴AC:BC=人高:人影=1:1,
∴AC=BC=DB+DC,
∵DB=32m,DC=×230m=115m,
∴AC=32m+115m=147m。
02
知识精讲
当物体的高度不能直接测量时,通常用“在平行光的照射下,在同一时刻,不同物体的物高与影长成比例”这一原理间接计算。
平行投影的应用
相关公式:
(1)物高:参照物高=物影:参照物影;
(2)物高:物影=参照物高:参照物影。
知识精讲
例、已知一直立的电线杆在地面上的影长为20m,同时,高为1.4m的测竿在地面上的影长为2.8m,由此可知该电线杆的长为__________m。
【分析】
设电线杆的长是x米,
由题意可得:1.4:2.8=x:20,
解得:x=10。
10
20m
2.8m
?
1.4m
03
典例精析
中心投影
夜晚,当人在路灯下行走时,会看到一个有趣的现象:在灯光照射范围内,离开路灯越远,影子就越长(如图)。
通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的。
01
情境引入
中心投影
投射线
投射面
点光源
02
知识精讲
在点光源的照射下,物体所产生的影称为中心投影。
中心投影的特点:投影线交于一点。
02
知识精讲
中心投影
一般地,在点光源的照射下,同一物体在不同位置,它的物高与影长不成比例。
练一练1-1:如图,三根旗杆的底部在同一条直线上,其中两根在同一灯光下的影长已画出。请在图中画出光源的位置,并画出另一根旗杆在该灯光下的影长。
点光源
02
知识精讲
练一练1-2:如图,过点光源向旗杆底部所在直线作垂直,你发现了什么?
点光源
02
知识精讲
可以构造“相似三角形”模型:
△ABC∽△OMC,
△DEF∽△OMF,
△GHI∽△OMI。
A
B
C
E
F
D
H
I
G
O
M
练一练2:如图,马路两侧有两根灯杆AB、CD。当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长为NE。测得BD=24m,NB=6m,NE=2m,判断这两根灯杆的高度是否相同,并说明理由。
2m
6m
24m
02
知识精讲
8m
02
知识精讲
【分析】
∵AB∥MN∥CD,
∴△ABE∽△MNE,△CDB∽△MNB,
∴=,=,
∴=,=,
∴AB=4MN=CD。
知识精讲
例1、(1)学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1)。如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线。请根据以上测量数据,帮助实践小组求出该古建筑的高度。
03
典例精析
23m
4m
2m
2m
2m
知识精讲
03
典例精析
【分析】设BE=xm,
∵AB∥EF∥GH,
∴△ABD∽△FED,△ABC∽△HGC,
∴=,=,
∵EF=HG=2,
∴=,∴=,解得:x=23,
∴=,即=,解得:AB=25m。
知识精讲
例1、(2)如图,一盏路灯(点O)距地面6.4m,身高1.6m的小明从距离路灯的底部(点P)9m的A处,沿AP所在的直线行走到点D处时,小明在路灯下的影子长度缩短了1.8m,求小明行走的距离。
9m
6.4m
1.6m
1.6m
03
典例精析
【分析】设DF=xm,则AC=(x+1.8)m,
∵OP∥DE∥AB,
∴△DEF∽△POF,△ABC∽△POC,
∴=,=,解得:PD=3.6m,
∴AD=AP-PD=9-3.6=5.4(m)。
知识精讲
例2、如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,路灯灯泡在点D正上方。
(1)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高。
P
03
典例精析
1.6m
1.4m
2.1m
3.5m
∵AB∥PD,∴△ABC∽△DPC,∴=,
∵AB=1.6m,AC=1.4m,AD=2.1m,
∴=,解得:DP=4m,
∴灯泡的高为4m。
【分析】(1)如图,点P即为设灯泡所在位置,
知识精讲
例2、如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,路灯灯泡在点D正上方。(1)DP=4m。
(2)在(1)的条件下当小明越过路灯到达FG时,发现影长和身高相等,求小明前行的路程。
03
典例精析
P
1.6m
E
∵GF∥PD,∴△FGE∽△DPE,∴=,
∵GF=EF=AB=1.6m,
∴DE=PD=4m,
∴AF=AD+DE-EF=2.1+4-1.6=4.5(m),
∴小明前行的路程为4.5m。
(2)如图,延长PG交CF的延长线于点E,EF即为影子长,
其他实际问题
知识精讲
例1、为了测量校园水平地面上一棵不可攀爬的树的高度,小文同学做了如下的探索:根据物理学中光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在合适的位置,刚好能在镜子里看到树梢顶点,此时小文与平面镜的水平距离为3.0米,树的底部与平面镜的水平距离为12.0米,若小文的眼睛与地面的距离为1.7米,则树的高度约为________米(注:反射角等于入射角)。
P
03
典例精析
镜面——对称相似
【分析】如图,过E作法线PE,
由题意可知:∠PEC=∠PEA,∠PED=∠PEB=90°,
∴∠CED=∠AEB,
又∵∠CDE=∠ABE=90°,
∴△CED∽△AEB,∴=,
知识精讲
例1、为了测量校园水平地面上一棵不可攀爬的树的高度,小文同学做了如下的探索:根据物理学中光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在合适的位置,刚好能在镜子里看到树梢顶点,此时小文与平面镜的水平距离为3.0米,树的底部与平面镜的水平距离为12.0米,若小文的眼睛与地面的距离为1.7米,则树的高度约为________米(注:反射角等于入射角)。
6.8
03
典例精析
镜面——对称相似
P
∵DE=3.0米,BE=12.0米,CD=1.7米,
∴=,解得:AB=6.8米,
∴树的高度约为6.8米。
知识精讲
例2、如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB。如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为________。
【分析】 ∵OA:OC=OB:OD=3,∠COD=∠AOB,
∴△COD∽△AOB,∴AB:CD=3,
∵CD=3cm,∴AB=9cm,
∵某零件的外径为10cm,
∴零件的厚度x为:(10-9)÷2=1÷2=0.5(cm)。
0.5cm
03
典例精析
“8”字问题——测长度
课后总结
在平行光的照射下,物体所产生的影称为平行投影。
在平行光的照射下:
(1)在同一时刻,不同物体的物高与影长成比例;
当物体的高度不能直接测量时,通常用这一原理间接计算。
相关公式:(1)物高:参照物高=物影:参照物影;(2)物高:物影=参照物高:参照物影。
(2)在不同时刻,同一物体的影长不相等。
在点光源的照射下,物体所产生的影称为中心投影。
一般地,在点光源的照射下,同一物体在不同位置,它的物高与影长不成比例。
6.7 用相似三角形解决问题
第6章 图形的相似
教学目标
01
认识平行投影,并会根据平行投影画图;能利用平行投影下物高与影长的关系原理进行相关测量和计算
02
03
能通过对实际问题的研究,进一步建立“相似三角形”模型,从而解决问题
认识中心投影,并会根据中心投影画图;能利用中心投影下物高与影长的关系原理进行相关测量和计算
平行投影
光在空气中传播时,遇到不透明的物体,在这个物体后面光不能到达的区域便产生影。
01
情境引入
如图,在太阳光的照射下,树木、路灯、路标都产生了影。
通常,我们把太阳光看成平行光。
01
情境引入
平行投影
【拓展】平行投影分为:
正投影:如图(1),把投射线垂直于投影面的平行投影叫做正投影;
斜投影:如图(2),把投射线不垂直于投影面的平行投影叫做斜投影。
(1)
(2)
投射线
投射面
02
知识精讲
在平行光的照射下,物体所产生的影称为平行投影。
【思考1】在阳光下,同一时刻,不同物体的高度与影长有什么关系
【操作1】在学校操场上分别竖立长度不同的甲、乙、丙三根木杆,在同一时刻分别测量这三根木杆在阳光下的影长,并将有关数据填入下表:
【结论1】在平行光的照射下,在同一时刻,不同物体的物高与影长成比例。
木杆 木杆长度 杆影长度
甲 80cm
乙 120cm
丙 160cm
02
知识精讲
杆影长度
16cm
24cm
32cm
5
5
5
【思考2】在阳光下,不同时刻,同一物体的影长相等吗
02
知识精讲
【操作2】在不用时刻分别测量甲根木杆在阳光下的影长,并将有关数据填入下表:
【结论2】在平行光的照射下,在不同时刻,同一物体的影长不相等。
木杆 木杆长度 杆影长度
甲 80cm
80cm
80cm
杆影长度
16cm
40cm
80cm
02
知识精讲
平行投影
在平行光的照射下:
(1)在同一时刻,不同物体的物高与影长成比例;
(2)在不同时刻,同一物体的影长不相等。
练一练1-1:如图,甲木杆AB在阳光下的影长为BC,试在图中画出同一时刻乙、丙两根木杆在阳光下的影长。
甲
乙
丙
02
知识精讲
练一练1-2:如何运用“三角形的相似知识”来说明“平行光线的照射下,同一时刻物高与影长成比例”?
甲
乙
丙
A
B
C
D
E
F
02
知识精讲
【分析】建立如图所示的模型,
∵AC∥DF,
∴∠C=∠F,
∵∠B=∠E=90°,
∴△ABC∽△DEF,
∴=,即=。
练一练2:在不能直接测量的情况下,怎样求旗杆的高度
A
B
O
A’
B’
O’
02
知识精讲
【原理】
在平行光的照射下,在同一时刻,
不同物体的物高与影长成比例。
【建模】如图,人的身高为O’B’=n,影长为A’B’=n,旗杆的影长为AB=m,求旗杆OB的高度。
02
知识精讲
【分析】
∵平行光,∴∠A=∠A’,
∵∠B=∠E=90°,∴△AOB∽△A’O’B’,
∴=,∴=,
∴=,即OB=。
02
知识精讲
【总结】
(1)=,即物高:参照物高=物影:参照物影;
(2)=,即物高:物影=参照物高:参照物影。
练一练3:古埃及国王曾请一位学者测量金字塔的高度。当这位学者确认在阳光下他的影长等于他的身高时(如图),要求他的助手同时测出金字塔的影长DB以及金字塔底部正方形的边长,这样他就知道了金字塔的高度。他是怎么算的呢?
02
知识精讲
【建模】如图,当学者的身高与影长相等时,测得金字塔的影长DB为32m,若金字塔底部正方形的边长为230m,你能帮助这位学者计算这座金字塔的高度吗?
02
知识精讲
【分析】
若无遮挡,AC对应的影长应为BC,
∴AC:BC=人高:人影=1:1,
∴AC=BC=DB+DC,
∵DB=32m,DC=×230m=115m,
∴AC=32m+115m=147m。
02
知识精讲
当物体的高度不能直接测量时,通常用“在平行光的照射下,在同一时刻,不同物体的物高与影长成比例”这一原理间接计算。
平行投影的应用
相关公式:
(1)物高:参照物高=物影:参照物影;
(2)物高:物影=参照物高:参照物影。
知识精讲
例、已知一直立的电线杆在地面上的影长为20m,同时,高为1.4m的测竿在地面上的影长为2.8m,由此可知该电线杆的长为__________m。
【分析】
设电线杆的长是x米,
由题意可得:1.4:2.8=x:20,
解得:x=10。
10
20m
2.8m
?
1.4m
03
典例精析
中心投影
夜晚,当人在路灯下行走时,会看到一个有趣的现象:在灯光照射范围内,离开路灯越远,影子就越长(如图)。
通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的。
01
情境引入
中心投影
投射线
投射面
点光源
02
知识精讲
在点光源的照射下,物体所产生的影称为中心投影。
中心投影的特点:投影线交于一点。
02
知识精讲
中心投影
一般地,在点光源的照射下,同一物体在不同位置,它的物高与影长不成比例。
练一练1-1:如图,三根旗杆的底部在同一条直线上,其中两根在同一灯光下的影长已画出。请在图中画出光源的位置,并画出另一根旗杆在该灯光下的影长。
点光源
02
知识精讲
练一练1-2:如图,过点光源向旗杆底部所在直线作垂直,你发现了什么?
点光源
02
知识精讲
可以构造“相似三角形”模型:
△ABC∽△OMC,
△DEF∽△OMF,
△GHI∽△OMI。
A
B
C
E
F
D
H
I
G
O
M
练一练2:如图,马路两侧有两根灯杆AB、CD。当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长为NE。测得BD=24m,NB=6m,NE=2m,判断这两根灯杆的高度是否相同,并说明理由。
2m
6m
24m
02
知识精讲
8m
02
知识精讲
【分析】
∵AB∥MN∥CD,
∴△ABE∽△MNE,△CDB∽△MNB,
∴=,=,
∴=,=,
∴AB=4MN=CD。
知识精讲
例1、(1)学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1)。如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线。请根据以上测量数据,帮助实践小组求出该古建筑的高度。
03
典例精析
23m
4m
2m
2m
2m
知识精讲
03
典例精析
【分析】设BE=xm,
∵AB∥EF∥GH,
∴△ABD∽△FED,△ABC∽△HGC,
∴=,=,
∵EF=HG=2,
∴=,∴=,解得:x=23,
∴=,即=,解得:AB=25m。
知识精讲
例1、(2)如图,一盏路灯(点O)距地面6.4m,身高1.6m的小明从距离路灯的底部(点P)9m的A处,沿AP所在的直线行走到点D处时,小明在路灯下的影子长度缩短了1.8m,求小明行走的距离。
9m
6.4m
1.6m
1.6m
03
典例精析
【分析】设DF=xm,则AC=(x+1.8)m,
∵OP∥DE∥AB,
∴△DEF∽△POF,△ABC∽△POC,
∴=,=,解得:PD=3.6m,
∴AD=AP-PD=9-3.6=5.4(m)。
知识精讲
例2、如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,路灯灯泡在点D正上方。
(1)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高。
P
03
典例精析
1.6m
1.4m
2.1m
3.5m
∵AB∥PD,∴△ABC∽△DPC,∴=,
∵AB=1.6m,AC=1.4m,AD=2.1m,
∴=,解得:DP=4m,
∴灯泡的高为4m。
【分析】(1)如图,点P即为设灯泡所在位置,
知识精讲
例2、如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,路灯灯泡在点D正上方。(1)DP=4m。
(2)在(1)的条件下当小明越过路灯到达FG时,发现影长和身高相等,求小明前行的路程。
03
典例精析
P
1.6m
E
∵GF∥PD,∴△FGE∽△DPE,∴=,
∵GF=EF=AB=1.6m,
∴DE=PD=4m,
∴AF=AD+DE-EF=2.1+4-1.6=4.5(m),
∴小明前行的路程为4.5m。
(2)如图,延长PG交CF的延长线于点E,EF即为影子长,
其他实际问题
知识精讲
例1、为了测量校园水平地面上一棵不可攀爬的树的高度,小文同学做了如下的探索:根据物理学中光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在合适的位置,刚好能在镜子里看到树梢顶点,此时小文与平面镜的水平距离为3.0米,树的底部与平面镜的水平距离为12.0米,若小文的眼睛与地面的距离为1.7米,则树的高度约为________米(注:反射角等于入射角)。
P
03
典例精析
镜面——对称相似
【分析】如图,过E作法线PE,
由题意可知:∠PEC=∠PEA,∠PED=∠PEB=90°,
∴∠CED=∠AEB,
又∵∠CDE=∠ABE=90°,
∴△CED∽△AEB,∴=,
知识精讲
例1、为了测量校园水平地面上一棵不可攀爬的树的高度,小文同学做了如下的探索:根据物理学中光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在合适的位置,刚好能在镜子里看到树梢顶点,此时小文与平面镜的水平距离为3.0米,树的底部与平面镜的水平距离为12.0米,若小文的眼睛与地面的距离为1.7米,则树的高度约为________米(注:反射角等于入射角)。
6.8
03
典例精析
镜面——对称相似
P
∵DE=3.0米,BE=12.0米,CD=1.7米,
∴=,解得:AB=6.8米,
∴树的高度约为6.8米。
知识精讲
例2、如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB。如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为________。
【分析】 ∵OA:OC=OB:OD=3,∠COD=∠AOB,
∴△COD∽△AOB,∴AB:CD=3,
∵CD=3cm,∴AB=9cm,
∵某零件的外径为10cm,
∴零件的厚度x为:(10-9)÷2=1÷2=0.5(cm)。
0.5cm
03
典例精析
“8”字问题——测长度
课后总结
在平行光的照射下,物体所产生的影称为平行投影。
在平行光的照射下:
(1)在同一时刻,不同物体的物高与影长成比例;
当物体的高度不能直接测量时,通常用这一原理间接计算。
相关公式:(1)物高:参照物高=物影:参照物影;(2)物高:物影=参照物高:参照物影。
(2)在不同时刻,同一物体的影长不相等。
在点光源的照射下,物体所产生的影称为中心投影。
一般地,在点光源的照射下,同一物体在不同位置,它的物高与影长不成比例。
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
