7.2.1 正弦、余弦-第1课时(同步课件)-2023-2024学年九年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 7.2.1 正弦、余弦-第1课时(同步课件)-2023-2024学年九年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
7.2.1正弦、余弦-第1课时
第7章 锐角三角函数
教学目标
01
理解锐角的正弦、余弦的概念,并掌握其计算公式
02
03
熟记特殊角的正弦、余弦值
理解并掌握锐角的正弦、余弦的增减性
正弦、余弦的概念
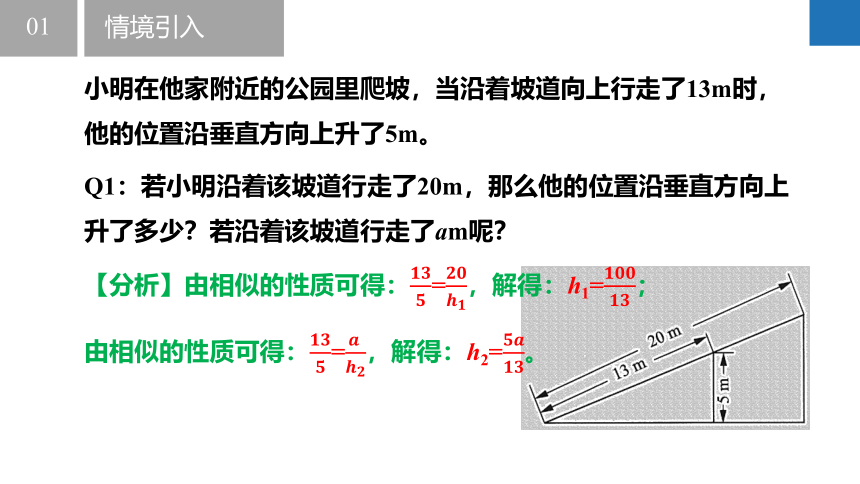
Q1:若小明沿着该坡道行走了20m,那么他的位置沿垂直方向上升了多少?若沿着该坡道行走了am呢?
小明在他家附近的公园里爬坡,当沿着坡道向上行走了13m时,他的位置沿垂直方向上升了5m。
01
情境引入
【分析】由相似的性质可得:=,解得:h1=;
由相似的性质可得:=,解得:h2=。
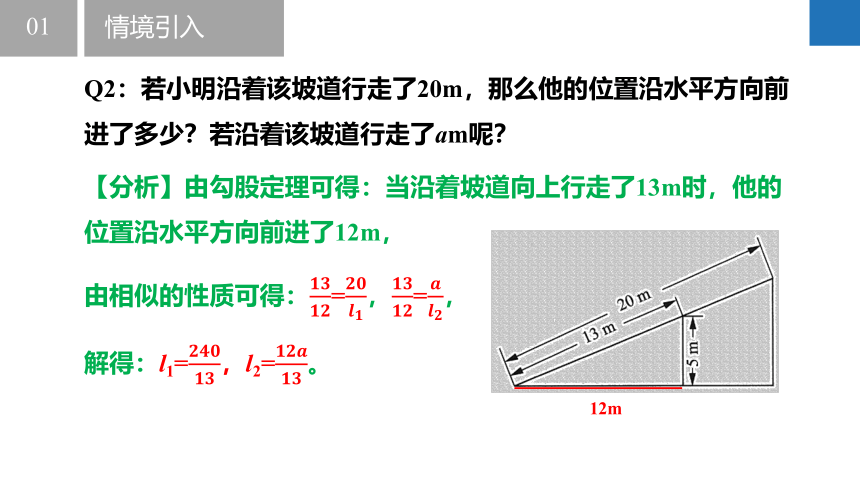
Q2:若小明沿着该坡道行走了20m,那么他的位置沿水平方向前进了多少?若沿着该坡道行走了am呢?
【分析】由勾股定理可得:当沿着坡道向上行走了13m时,他的位置沿水平方向前进了12m,
01
情境引入
12m
由相似的性质可得:=,=,
解得:l1=,l2=。
Q3:当直角三角形的一个锐角的大小确定时,它的对边与斜边的比值、邻边与斜边的比值是否为定值?
12m
【结论】当直角三角形的一个锐角的大小确定时,它的对边与斜边的比值、邻边与斜边的比值为定值。
01
情境引入
【分析】=,变形得:=,即为定值;
=,变形得:=,即为定值。
正弦、余弦
02
知识精讲
【正弦、余弦的概念】
如图,在Rt△ABC中,∠C=90°,
我们把∠A的对边a与斜边c的比,叫做∠A的正弦,记作sinA,sinA==;
我们把∠A的邻边b与斜边c的比,叫做∠A的余弦,记作cosA,cosA==。
02
知识精讲
练一练1:判断对错:
(1)如图,cosA= ( )
(2)如图,sinA= ( )
(2)
(1)
A
B
C
A
B
C
×
×
余弦是在直角三角形中定义的
sinA==
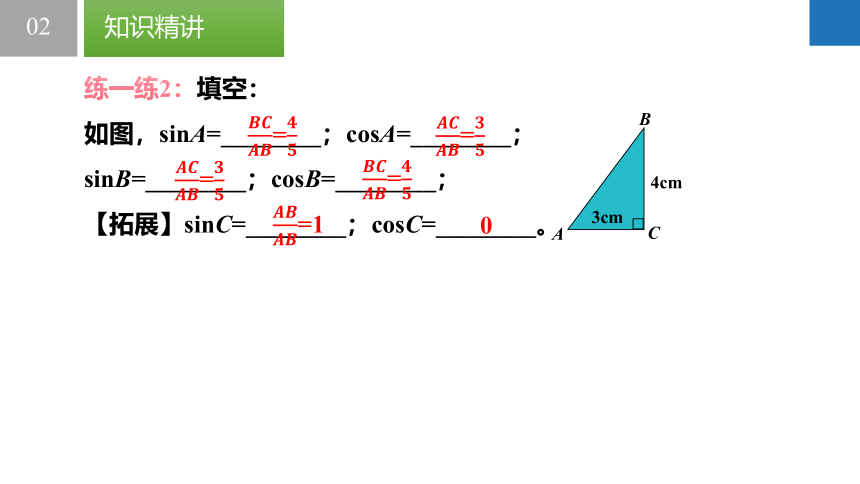
练一练2:填空:
如图,sinA=________;cosA=________;
sinB=________;cosB=________;
【拓展】sinC=________;cosC=________。
02
知识精讲
A
B
C
4cm
3cm
=
=
=
=
=1
0
02
知识精讲
【注意点】与正切类似
(1)正、余弦也是在直角▲中定义的,初中阶段,也只研究锐角的正、余弦;
(2)sinA、cosA也是一个完整的符号,分别表示∠A的正、余弦,不要误以为是“sin”乘以“A”或“cos”乘以“A”;
(3)正弦的正确记法:sinA、sin∠BAC、sin∠1;余弦的正确记法:cosA、cos∠BAC、cos∠1;
(4)sinA、cosA的大小也只与∠A的大小有关,与直角▲的边长无关(我们只是利用边长计算数值而已)
(5)sinA、cosA也没有单位。
知识精讲
例1、(1)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinA的值是________。
03
典例精析
A
B
C
4
3
【分析】在Rt△ABC中,
∵∠C=90°,AC=4,BC=3,
∴AB=5,
∴sinA==。
知识精讲
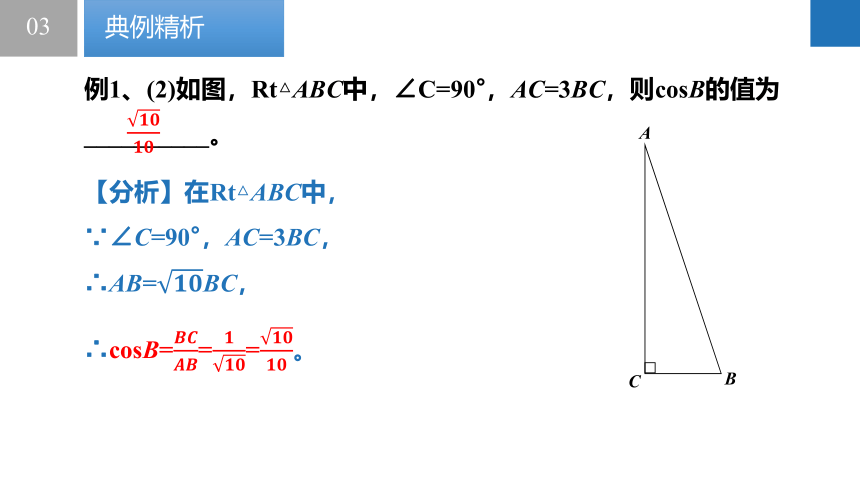
例1、(2)如图,Rt△ABC中,∠C=90°,AC=3BC,则cosB的值为__________。
03
典例精析
A
B
C
【分析】在Rt△ABC中,
∵∠C=90°,AC=3BC,
∴AB=BC,
∴cosB===。
知识精讲
例1、(3)在Rt△ABC中,∠C=90°,AB=26,sinA=,那么BC的长为__________。
03
典例精析
A
B
C
26
10
【分析】如图,在Rt△ABC中,
∵∠C=90°,AB=13,sinA=,
∴=,即=,解得:BC=10。
知识精讲
例1、(4)在Rt△ABC中,∠C=90°,BC=6,cosB=,那么AC的长为__________。
03
典例精析
A
B
C
6
【分析】如图,在Rt△ABC中,
∵∠C=90°,BC=6,cosB=,
∴=,即=,解得:AB=8,
∴AC=2。
2
知识精讲
例2、由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正弦值为________,余弦值为________。
03
典例精析
【分析】如图,连接AC,
由图可知:AC=BC=,
取AB中点D,连接CD,则CD⊥AB,即∠BCD=90°,
D
由图可知:CD=,BD=2,
∴sin∠ABC===,cos∠ABC===。
正弦、余弦的增减性
如图,当一个点从原点O出发,沿着15°线移动了1个单位长度到点P时,这个点在垂直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度。
01
情境引入
于是,可知sin15°≈0.26,cos15°≈0.97。
【分析】如图,一个点从原点O出发,沿着75°线移动了1个单位长度到点Q,
Q
Q1:你能写出sin75°、cos75°的近似值吗?
01
情境引入
∵这个点在垂直方向上升了约0.97个单位长度,在水平方向前进了约0.26个单位长度,
∴sin75°≈0.97,cos75°≈0.26。
【结论】锐角的正弦值会随锐角的增大而增大,余弦值会随锐角的增大而减小。
【分析】如图,一个点从原点O出发,沿着θ线移动了1个单位长度到点M,
Q2:随着锐角θ的增大,sinθ与cosθ的值怎样变化?
01
情境引入
M1
M2
M3
∵随着锐角θ的增大,点M的垂直高度的距离h在增大,水平方向的距离l在减小,
∴sinθ==h,cos75°==l。
Q3:如图,分别计算30°、45°、60°的正弦、余弦值,并分别比较三个角的正弦、余弦值的大小。
45°
1
1
30°
60°
1
2
01
情境引入
sin30°=,cos30°=
sin60°=,cos60°=
sin45°=,cos45°=
【分析】
∵30°<45°<60°,
∴sin30°cos30°>cos45°>cos60°。
特殊角的正弦、余弦值与正弦、余弦的增减性
【正弦、余弦的增减性】
锐角的正弦值会随锐角的增大而增大,余弦值会随锐角的增大而减小。
θ=30° θ=45° θ=60°
sinθ
cosθ
02
知识精讲
议一议1:如图,探究sinθ的临界值~(θ为锐角)
02
知识精讲
【分析】
∵锐角的正弦值会随锐角的增大而增大,
∴sin0°∵sin0°==0,sin90°==1,
∴0议一议2:如图,探究cosθ的临界值~(θ为锐角)
02
知识精讲
【分析】
∵锐角的余弦值会随锐角的增大而减小,
∴cos90°∵cos90°==0,cos0°==1,
∴0锐角的正弦、余弦值的范围
范围
sinθ(θ为锐角) 0cosθ(θ为锐角) 002
知识精讲
例1、(1)如果∠A为锐角,sinA=,那么( )
A.0°<∠A<30° B.30°<∠A<45°
C.45°<∠A<60° D.60°<∠A<90°
A
03
典例精析
θ=30° θ=45° θ=60°
sinθ
例1、(2)已知cosα=0.75,则锐角α的取值范围是( )
A.0°<α<30° B.30°<α<45°
C.45°<α<60° D.60°<α<90°
B
θ=30° θ=45° θ=60°
cosθ
03
典例精析
例3、比较大小:sin81°________tan47°(填“<”、“=”或“>”)。
<
【分析】
∵sin81°<sin90°=1,tan47°>tan45°=1,
∴sin81°<1<tan47°,
∴sin81°<tan47°。
03
典例精析
课后总结
【正弦、余弦的概念】
如图,在Rt△ABC中,∠C=90°,
∠A的对边a与斜边c的比,叫做∠A的正弦,记作sinA,sinA==;
∠A的邻边b与斜边c的比,叫做∠A的余弦,记作cosA,cosA==。
课后总结
【注意点】与正切类似
(1)正、余弦也是在直角▲中定义的,初中阶段,也只研究锐角的正、余弦;
(2)sinA、cosA也是一个完整的符号,分别表示∠A的正、余弦,不要误以为是“sin”乘以“A”或“cos”乘以“A”;
(3)正弦的正确记法:sinA、sin∠BAC、sin∠1;余弦的正确记法:cosA、cos∠BAC、cos∠1;
(4)sinA、cosA的大小也只与∠A的大小有关,与直角▲的边长无关(我们只是利用边长计算数值而已)
(5)sinA、cosA也没有单位。
课后总结
θ=30° θ=45° θ=60°
sinθ
cosθ
【正弦、余弦的增减性】
锐角的正弦值会随锐角的增大而增大,余弦值会随锐角的增大而减小。
范围
sinθ(θ为锐角) 0cosθ(θ为锐角) 0
7.2.1正弦、余弦-第1课时
第7章 锐角三角函数
教学目标
01
理解锐角的正弦、余弦的概念,并掌握其计算公式
02
03
熟记特殊角的正弦、余弦值
理解并掌握锐角的正弦、余弦的增减性
正弦、余弦的概念
Q1:若小明沿着该坡道行走了20m,那么他的位置沿垂直方向上升了多少?若沿着该坡道行走了am呢?
小明在他家附近的公园里爬坡,当沿着坡道向上行走了13m时,他的位置沿垂直方向上升了5m。
01
情境引入
【分析】由相似的性质可得:=,解得:h1=;
由相似的性质可得:=,解得:h2=。
Q2:若小明沿着该坡道行走了20m,那么他的位置沿水平方向前进了多少?若沿着该坡道行走了am呢?
【分析】由勾股定理可得:当沿着坡道向上行走了13m时,他的位置沿水平方向前进了12m,
01
情境引入
12m
由相似的性质可得:=,=,
解得:l1=,l2=。
Q3:当直角三角形的一个锐角的大小确定时,它的对边与斜边的比值、邻边与斜边的比值是否为定值?
12m
【结论】当直角三角形的一个锐角的大小确定时,它的对边与斜边的比值、邻边与斜边的比值为定值。
01
情境引入
【分析】=,变形得:=,即为定值;
=,变形得:=,即为定值。
正弦、余弦
02
知识精讲
【正弦、余弦的概念】
如图,在Rt△ABC中,∠C=90°,
我们把∠A的对边a与斜边c的比,叫做∠A的正弦,记作sinA,sinA==;
我们把∠A的邻边b与斜边c的比,叫做∠A的余弦,记作cosA,cosA==。
02
知识精讲
练一练1:判断对错:
(1)如图,cosA= ( )
(2)如图,sinA= ( )
(2)
(1)
A
B
C
A
B
C
×
×
余弦是在直角三角形中定义的
sinA==
练一练2:填空:
如图,sinA=________;cosA=________;
sinB=________;cosB=________;
【拓展】sinC=________;cosC=________。
02
知识精讲
A
B
C
4cm
3cm
=
=
=
=
=1
0
02
知识精讲
【注意点】与正切类似
(1)正、余弦也是在直角▲中定义的,初中阶段,也只研究锐角的正、余弦;
(2)sinA、cosA也是一个完整的符号,分别表示∠A的正、余弦,不要误以为是“sin”乘以“A”或“cos”乘以“A”;
(3)正弦的正确记法:sinA、sin∠BAC、sin∠1;余弦的正确记法:cosA、cos∠BAC、cos∠1;
(4)sinA、cosA的大小也只与∠A的大小有关,与直角▲的边长无关(我们只是利用边长计算数值而已)
(5)sinA、cosA也没有单位。
知识精讲
例1、(1)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinA的值是________。
03
典例精析
A
B
C
4
3
【分析】在Rt△ABC中,
∵∠C=90°,AC=4,BC=3,
∴AB=5,
∴sinA==。
知识精讲
例1、(2)如图,Rt△ABC中,∠C=90°,AC=3BC,则cosB的值为__________。
03
典例精析
A
B
C
【分析】在Rt△ABC中,
∵∠C=90°,AC=3BC,
∴AB=BC,
∴cosB===。
知识精讲
例1、(3)在Rt△ABC中,∠C=90°,AB=26,sinA=,那么BC的长为__________。
03
典例精析
A
B
C
26
10
【分析】如图,在Rt△ABC中,
∵∠C=90°,AB=13,sinA=,
∴=,即=,解得:BC=10。
知识精讲
例1、(4)在Rt△ABC中,∠C=90°,BC=6,cosB=,那么AC的长为__________。
03
典例精析
A
B
C
6
【分析】如图,在Rt△ABC中,
∵∠C=90°,BC=6,cosB=,
∴=,即=,解得:AB=8,
∴AC=2。
2
知识精讲
例2、由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正弦值为________,余弦值为________。
03
典例精析
【分析】如图,连接AC,
由图可知:AC=BC=,
取AB中点D,连接CD,则CD⊥AB,即∠BCD=90°,
D
由图可知:CD=,BD=2,
∴sin∠ABC===,cos∠ABC===。
正弦、余弦的增减性
如图,当一个点从原点O出发,沿着15°线移动了1个单位长度到点P时,这个点在垂直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度。
01
情境引入
于是,可知sin15°≈0.26,cos15°≈0.97。
【分析】如图,一个点从原点O出发,沿着75°线移动了1个单位长度到点Q,
Q
Q1:你能写出sin75°、cos75°的近似值吗?
01
情境引入
∵这个点在垂直方向上升了约0.97个单位长度,在水平方向前进了约0.26个单位长度,
∴sin75°≈0.97,cos75°≈0.26。
【结论】锐角的正弦值会随锐角的增大而增大,余弦值会随锐角的增大而减小。
【分析】如图,一个点从原点O出发,沿着θ线移动了1个单位长度到点M,
Q2:随着锐角θ的增大,sinθ与cosθ的值怎样变化?
01
情境引入
M1
M2
M3
∵随着锐角θ的增大,点M的垂直高度的距离h在增大,水平方向的距离l在减小,
∴sinθ==h,cos75°==l。
Q3:如图,分别计算30°、45°、60°的正弦、余弦值,并分别比较三个角的正弦、余弦值的大小。
45°
1
1
30°
60°
1
2
01
情境引入
sin30°=,cos30°=
sin60°=,cos60°=
sin45°=,cos45°=
【分析】
∵30°<45°<60°,
∴sin30°
特殊角的正弦、余弦值与正弦、余弦的增减性
【正弦、余弦的增减性】
锐角的正弦值会随锐角的增大而增大,余弦值会随锐角的增大而减小。
θ=30° θ=45° θ=60°
sinθ
cosθ
02
知识精讲
议一议1:如图,探究sinθ的临界值~(θ为锐角)
02
知识精讲
【分析】
∵锐角的正弦值会随锐角的增大而增大,
∴sin0°
∴0
02
知识精讲
【分析】
∵锐角的余弦值会随锐角的增大而减小,
∴cos90°
∴0
范围
sinθ(θ为锐角) 0
知识精讲
例1、(1)如果∠A为锐角,sinA=,那么( )
A.0°<∠A<30° B.30°<∠A<45°
C.45°<∠A<60° D.60°<∠A<90°
A
03
典例精析
θ=30° θ=45° θ=60°
sinθ
例1、(2)已知cosα=0.75,则锐角α的取值范围是( )
A.0°<α<30° B.30°<α<45°
C.45°<α<60° D.60°<α<90°
B
θ=30° θ=45° θ=60°
cosθ
03
典例精析
例3、比较大小:sin81°________tan47°(填“<”、“=”或“>”)。
<
【分析】
∵sin81°<sin90°=1,tan47°>tan45°=1,
∴sin81°<1<tan47°,
∴sin81°<tan47°。
03
典例精析
课后总结
【正弦、余弦的概念】
如图,在Rt△ABC中,∠C=90°,
∠A的对边a与斜边c的比,叫做∠A的正弦,记作sinA,sinA==;
∠A的邻边b与斜边c的比,叫做∠A的余弦,记作cosA,cosA==。
课后总结
【注意点】与正切类似
(1)正、余弦也是在直角▲中定义的,初中阶段,也只研究锐角的正、余弦;
(2)sinA、cosA也是一个完整的符号,分别表示∠A的正、余弦,不要误以为是“sin”乘以“A”或“cos”乘以“A”;
(3)正弦的正确记法:sinA、sin∠BAC、sin∠1;余弦的正确记法:cosA、cos∠BAC、cos∠1;
(4)sinA、cosA的大小也只与∠A的大小有关,与直角▲的边长无关(我们只是利用边长计算数值而已)
(5)sinA、cosA也没有单位。
课后总结
θ=30° θ=45° θ=60°
sinθ
cosθ
【正弦、余弦的增减性】
锐角的正弦值会随锐角的增大而增大,余弦值会随锐角的增大而减小。
范围
sinθ(θ为锐角) 0
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
