27.3 垂径定理 课件(共28张PPT)
文档属性
| 名称 | 27.3 垂径定理 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 09:50:36 | ||
图片预览





文档简介
(共28张PPT)
27.3 垂径定理
第27章 圆与正多边形
教师
xxx
沪教版 九年级第二学期
圆的轴对称性
垂径定理作辅助线的常用方法
垂径定理及推论
01
03
02
CONTANTS
目 录
圆的轴对称性
01
中国汉代数学典籍《九章算术》勾股章所记载的“圆材埋壁”问题,原文:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:现有圆柱状的木材,埋在墙壁里。不知道其大小,于是用锯子(沿横截面)锯它,当量得深度为一寸的时候,锯开的宽度为一尺,问木材的直径是多少?(一尺等于十寸)
用数学语言可表述为:“如图,在⊙O中,弦CD=10寸,弓形高AB=1寸,求直径的长。”
·
O
C
D
B
A
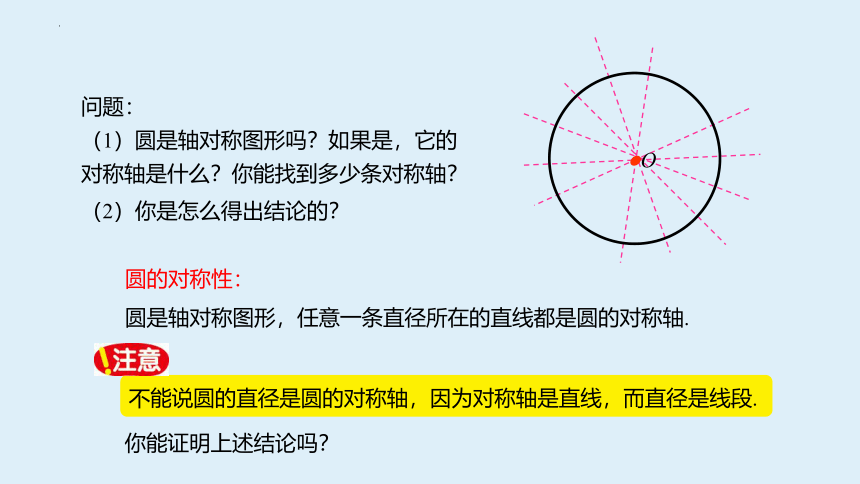
问题:
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
(2)你是怎么得出结论的?
圆的对称性:
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
●O
不能说圆的直径是圆的对称轴,因为对称轴是直线,而直径是线段.
你能证明上述结论吗?
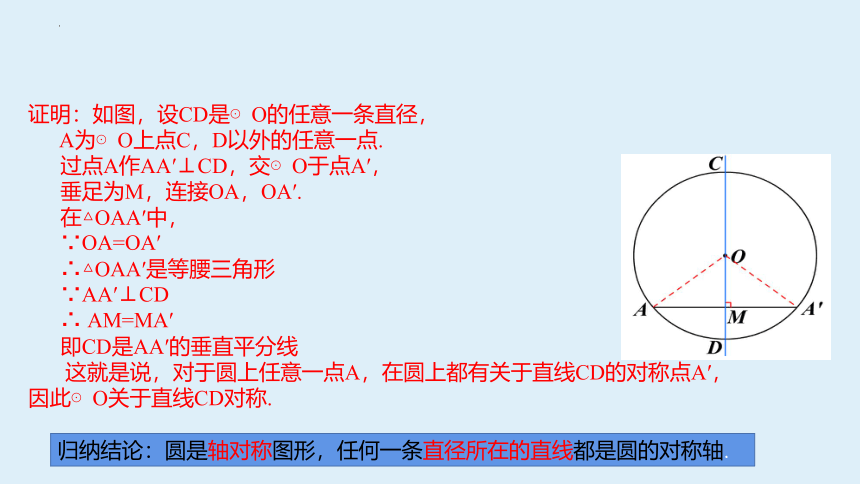
证明:如图,设CD是⊙O的任意一条直径,
A为⊙O上点C,D以外的任意一点.
过点A作AA′⊥CD,交⊙O于点A′,
垂足为M,连接OA,OA′.
在△OAA′中,
∵OA=OA′
∴△OAA′是等腰三角形
∵AA′⊥CD
∴ AM=MA′
即CD是AA′的垂直平分线
这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A′,因此⊙O关于直线CD对称.
归纳结论:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
垂径定理及推论
02
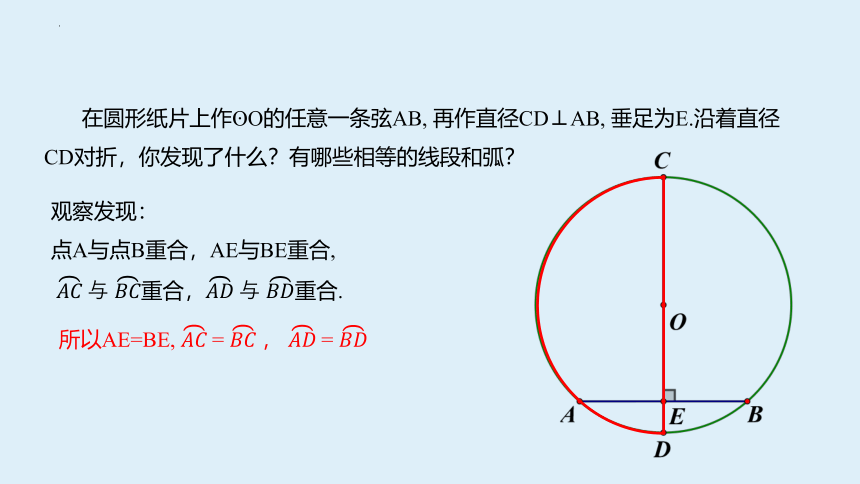
在圆形纸片上作 O的任意一条弦AB, 再作直径CD⊥AB, 垂足为E.沿着直径CD对折,你发现了什么?有哪些相等的线段和弧?
观察发现:
点A与点B重合,AE与BE重合,
重合, 重合.
所以AE=BE, = , =
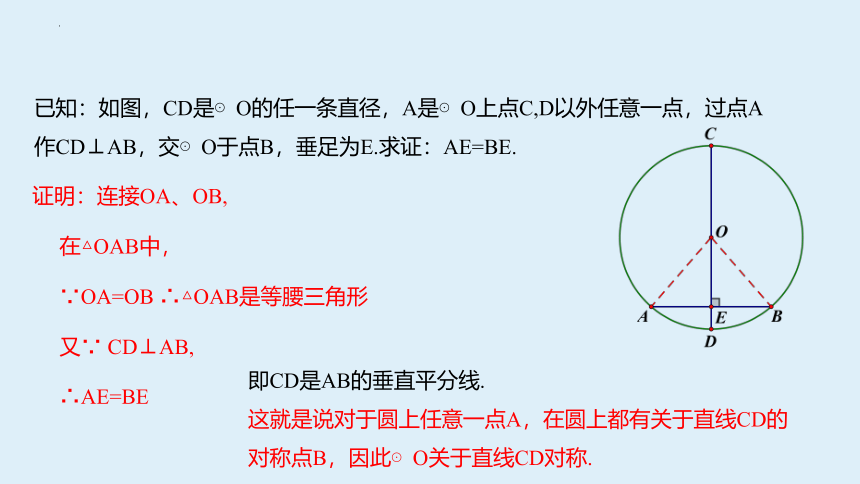
已知:如图,CD是⊙O的任一条直径,A是⊙O上点C,D以外任意一点,过点A作CD⊥AB,交⊙O于点B,垂足为E.求证:AE=BE.
证明:连接OA、OB,
在△OAB中,
∵OA=OB ∴△OAB是等腰三角形
又∵ CD⊥AB,
∴AE=BE
即CD是AB的垂直平分线.
这就是说对于圆上任意一点A,在圆上都有关于直线CD的对称点B,因此⊙O关于直线CD对称.
这样,我们就得到垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
符号语言:
∵CD是⊙O的直径,CD⊥AB
∴AE=BE,,
定理中的两个条件缺一不可:
①过圆心(直径);
②垂直于弦.
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心 ;
②垂直于弦;
③平分弦(非直径);
④平分弦所对的优弧 ;
⑤平分弦所对的劣弧.
在一个圆中,一条直线只要满足上面五个条件中的任意两个,可以推出其他三个结论吗?
A
B
O
C
D
E
问题:如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
(2)根据图形对称性可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
解:(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
⌒
⌒
⌒
·
O
A
B
C
D
E
已知条件“知二”
∵CD为直接 ∴已知①过圆心 ;
∵AE=BE ∴已知③平分弦(非直径);
结论“推三”:
CD⊥AB(②垂直于弦)
AC=BC(④平分弦所对的优弧 )
AD=BD(⑤平分弦所对的劣弧)
问题:如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
⌒
⌒
⌒
·
O
A
B
C
D
E
⌒
⌒
⌒
⌒
当弦AB为直径时,相关结论还成立吗?
·
O
A
B
C
D
“不是直径”这个条件不能去掉,因为当AB、CD互相平分且是直径时,虽然“知二”,但AB不一定垂直CD。
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理的推论
·
O
A
B
C
D
例1 赵州桥(如图)是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(结果保留小数点后一位).
分析:解决此问题的关键是根据赵州桥的实物图画出几何图形.
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
⌒
⌒
经过圆心O作弦AB的垂线OC,D为垂足,OC与AB相交于点C,连接OA.根据垂径定理,D是AB的中点,C是AB的中点,CD就是拱高.
⌒
⌒
由题设可知,AB=37m,CD=7.23m
所以,AD=AB=×37=18.5(m),OD=OC-CD=R-7.23
在Rt△OAD中,由勾股定理,得
OA2=AD2+OD2
即 R2=18.52+(R-7.23)2
解得 R≈27.3(m)
因此,赵州桥的主桥拱半径约为27.3m
垂径定理作辅助线的常用方法
03
归纳总结
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
弦a,弦心距d,弓形高h,半径r之间有以下关系:
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
弓形中重要数量关系
涉及垂径定理时辅助线的添加方法
1.如图,在⊙O中,弦AB的长为8 cm,圆心O到AB的距离为3 cm.
求⊙O的半径.
由图可知,AE=BE= AB
∵OE=3cm,AB=8cm,
∴BC=4cm
在Rt△OEA中,OA= 4 +3 =5cm
即⊙O的半径是5cm.
1
2
课堂练习
2.如图,已知⊙O的直径AB⊥CD于点E,则下列结论中错误的是( )
A.CE=DE
B.AE=OE
C. BC=BD
D.△OCE≌△ODE
⌒
⌒
B
D
3.如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中
不一正确的是( )
A.∠COE=∠DOE
B.CE=DE
C.
D.OE=BE
4.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为点N,
则ON=( )
A.5 B.7
C.9 D.11
5.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=12,BE=2,
则⊙O的直径为( )
A.8 B.10
C.16 D.20
A
D
6.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,
B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于
点F,则EF=( )
A.4
B.5
C.5.5
D.6
B
7.如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴
交于点B,C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,
OC=6,则⊙O′的半径为( )
A.7
B.6
C.5
D.4
C
8.如图,已知⊙O的半径为5,弦AB=8,P是弦
AB上一点,且PB=2, 求 OP的长.
感谢观看
27.3 垂径定理
第27章 圆与正多边形
教师
xxx
沪教版 九年级第二学期
圆的轴对称性
垂径定理作辅助线的常用方法
垂径定理及推论
01
03
02
CONTANTS
目 录
圆的轴对称性
01
中国汉代数学典籍《九章算术》勾股章所记载的“圆材埋壁”问题,原文:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:现有圆柱状的木材,埋在墙壁里。不知道其大小,于是用锯子(沿横截面)锯它,当量得深度为一寸的时候,锯开的宽度为一尺,问木材的直径是多少?(一尺等于十寸)
用数学语言可表述为:“如图,在⊙O中,弦CD=10寸,弓形高AB=1寸,求直径的长。”
·
O
C
D
B
A
问题:
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
(2)你是怎么得出结论的?
圆的对称性:
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
●O
不能说圆的直径是圆的对称轴,因为对称轴是直线,而直径是线段.
你能证明上述结论吗?
证明:如图,设CD是⊙O的任意一条直径,
A为⊙O上点C,D以外的任意一点.
过点A作AA′⊥CD,交⊙O于点A′,
垂足为M,连接OA,OA′.
在△OAA′中,
∵OA=OA′
∴△OAA′是等腰三角形
∵AA′⊥CD
∴ AM=MA′
即CD是AA′的垂直平分线
这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A′,因此⊙O关于直线CD对称.
归纳结论:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
垂径定理及推论
02
在圆形纸片上作 O的任意一条弦AB, 再作直径CD⊥AB, 垂足为E.沿着直径CD对折,你发现了什么?有哪些相等的线段和弧?
观察发现:
点A与点B重合,AE与BE重合,
重合, 重合.
所以AE=BE, = , =
已知:如图,CD是⊙O的任一条直径,A是⊙O上点C,D以外任意一点,过点A作CD⊥AB,交⊙O于点B,垂足为E.求证:AE=BE.
证明:连接OA、OB,
在△OAB中,
∵OA=OB ∴△OAB是等腰三角形
又∵ CD⊥AB,
∴AE=BE
即CD是AB的垂直平分线.
这就是说对于圆上任意一点A,在圆上都有关于直线CD的对称点B,因此⊙O关于直线CD对称.
这样,我们就得到垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
符号语言:
∵CD是⊙O的直径,CD⊥AB
∴AE=BE,,
定理中的两个条件缺一不可:
①过圆心(直径);
②垂直于弦.
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心 ;
②垂直于弦;
③平分弦(非直径);
④平分弦所对的优弧 ;
⑤平分弦所对的劣弧.
在一个圆中,一条直线只要满足上面五个条件中的任意两个,可以推出其他三个结论吗?
A
B
O
C
D
E
问题:如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
(2)根据图形对称性可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
解:(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
⌒
⌒
⌒
·
O
A
B
C
D
E
已知条件“知二”
∵CD为直接 ∴已知①过圆心 ;
∵AE=BE ∴已知③平分弦(非直径);
结论“推三”:
CD⊥AB(②垂直于弦)
AC=BC(④平分弦所对的优弧 )
AD=BD(⑤平分弦所对的劣弧)
问题:如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
⌒
⌒
⌒
·
O
A
B
C
D
E
⌒
⌒
⌒
⌒
当弦AB为直径时,相关结论还成立吗?
·
O
A
B
C
D
“不是直径”这个条件不能去掉,因为当AB、CD互相平分且是直径时,虽然“知二”,但AB不一定垂直CD。
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理的推论
·
O
A
B
C
D
例1 赵州桥(如图)是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(结果保留小数点后一位).
分析:解决此问题的关键是根据赵州桥的实物图画出几何图形.
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
⌒
⌒
经过圆心O作弦AB的垂线OC,D为垂足,OC与AB相交于点C,连接OA.根据垂径定理,D是AB的中点,C是AB的中点,CD就是拱高.
⌒
⌒
由题设可知,AB=37m,CD=7.23m
所以,AD=AB=×37=18.5(m),OD=OC-CD=R-7.23
在Rt△OAD中,由勾股定理,得
OA2=AD2+OD2
即 R2=18.52+(R-7.23)2
解得 R≈27.3(m)
因此,赵州桥的主桥拱半径约为27.3m
垂径定理作辅助线的常用方法
03
归纳总结
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
弦a,弦心距d,弓形高h,半径r之间有以下关系:
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
弓形中重要数量关系
涉及垂径定理时辅助线的添加方法
1.如图,在⊙O中,弦AB的长为8 cm,圆心O到AB的距离为3 cm.
求⊙O的半径.
由图可知,AE=BE= AB
∵OE=3cm,AB=8cm,
∴BC=4cm
在Rt△OEA中,OA= 4 +3 =5cm
即⊙O的半径是5cm.
1
2
课堂练习
2.如图,已知⊙O的直径AB⊥CD于点E,则下列结论中错误的是( )
A.CE=DE
B.AE=OE
C. BC=BD
D.△OCE≌△ODE
⌒
⌒
B
D
3.如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中
不一正确的是( )
A.∠COE=∠DOE
B.CE=DE
C.
D.OE=BE
4.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为点N,
则ON=( )
A.5 B.7
C.9 D.11
5.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=12,BE=2,
则⊙O的直径为( )
A.8 B.10
C.16 D.20
A
D
6.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,
B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于
点F,则EF=( )
A.4
B.5
C.5.5
D.6
B
7.如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴
交于点B,C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,
OC=6,则⊙O′的半径为( )
A.7
B.6
C.5
D.4
C
8.如图,已知⊙O的半径为5,弦AB=8,P是弦
AB上一点,且PB=2, 求 OP的长.
感谢观看
