27.5 圆与圆的位置关系 课件(共26张PPT)
文档属性
| 名称 | 27.5 圆与圆的位置关系 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 10:03:04 | ||
图片预览





文档简介
(共26张PPT)
27.5 圆与圆的位置关系
第27章 圆与正多边形
教师
xxx
沪教版 九年级第二学期
圆与圆的位置关系
相交(切)圆连心线的性质
01
03
02
CONTANTS
目 录
圆与圆的位置关系
01
生活中常见的圆与圆之间的位置关系
在上面的情景中,你能发现两圆的哪些不同的位置?分别用不同颜色的两圆,尝试在展示板上展示出来.
O
O’
观察⊙O与⊙O’在接近过程中的位置关系?
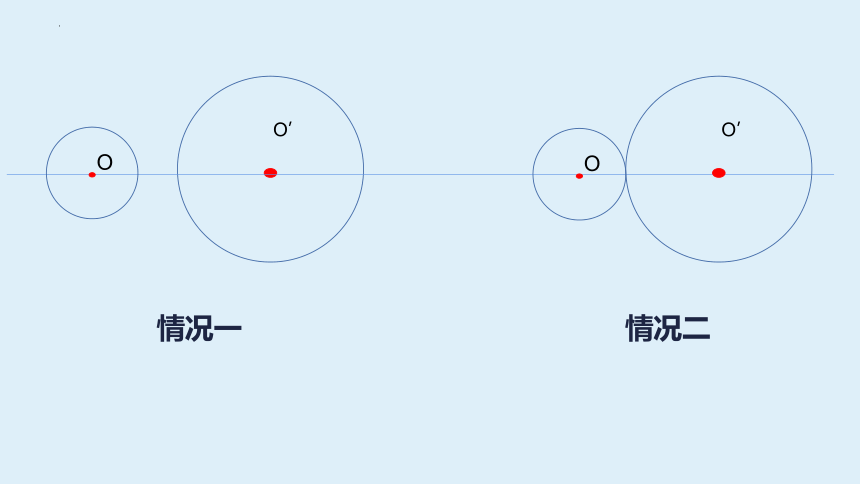
小组讨论:画出⊙O与⊙O’可能出现的情况
情况一
情况二
O’
O
O’
O
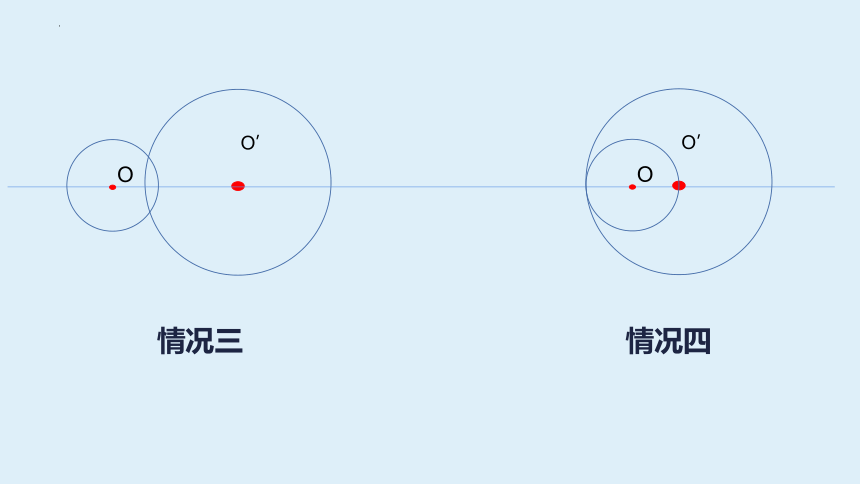
情况三
情况四
O’
O
O’
O
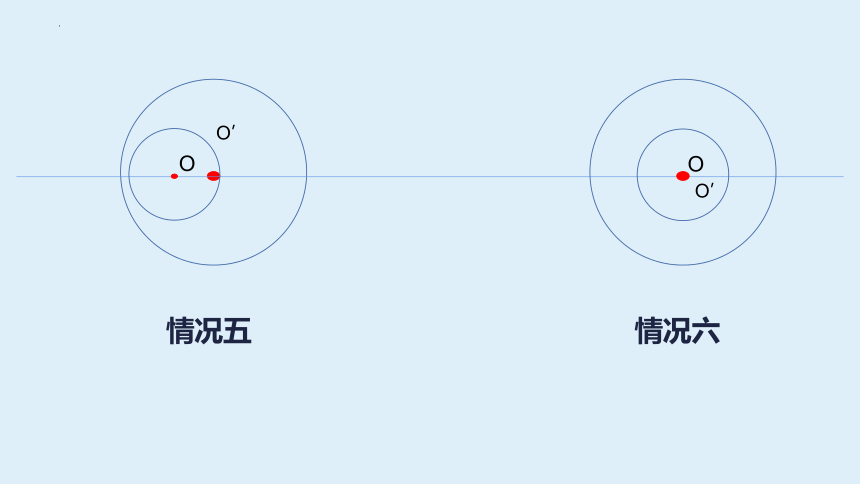
情况五
情况六
O’
O
O’
O
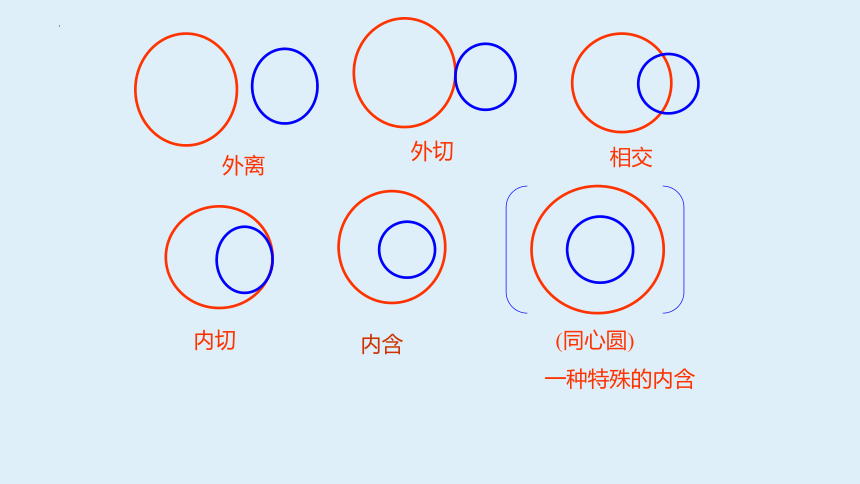
外离
外切
相交
内切
(同心圆)
一种特殊的内含
内含
两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.
外离
内含
两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.
两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切,这个惟一的公共点叫做切点.
外切
内切
两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切,这个惟一的公共点叫做切点.
两个圆有两个公共点时,叫做这两个圆相交.
O
2
O
1
相交
问题:能否从两圆公共点的个数来归纳两圆的位置关系?
答:无交点:
相离
外离
内含
有一个交点:
相切
外切
内切
有两个交点:
相交
结论:在同一平面内任意两圆只存在以上三类五种位置关系.
我们发现,我们研究的都是两个半径不同的圆,如果两圆半径相等,是不是也是这五种位置关系呢?
半径不同
d =R+r
d =R-r
d =0
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
当圆心距和半径满足这些关系时,能否得到相应的位置关系吗?
如果我们把两圆圆心的距离记做d(圆心距),大圆的半径记做R,小圆的半径记做r.
两圆的三类五种位置关系下圆心距和两圆半径的数量关系:
两圆外离
d>R1+R2
两圆外切
d= R1+R2
两圆相交
∣R1-R2∣<d<R1+R2
两圆内切
0<d= ∣R1-R2∣
两圆内含
0≤d<∣R1-R2∣
无交点:
两圆相离
有一个交点:
两圆相切
有两个交点:
两圆相交
1.已知两圆半径分别为6.5cm和3cm,圆心距为3.5cm,则两圆的位置关系是( )
A.相交 B.外切 C.内切 D.内含
【详解】
∵两圆的半径分别为6.5cm和3cm,圆心距为3.5cm,且6.5﹣3=3.5,
∴两圆的位置关系是内切.
故选:C.
练一练
2.两圆的半径分别是3㎝和5㎝,圆心距是8㎝,则两圆位置关系是( )
A.相离 B.相交 C.外切 D.内切
【详解】
解:因为3+5=8,圆心距为8,
由于两圆外切时,圆心距等于两圆半径的和,
故两圆外切.
故选:C.
3.⊙的直径,在延长线上,,若⊙与⊙有公共点,那么⊙的半径的取值范围是______________.
【详解】
解:因为3+5=8,圆心距为8,
由于两圆外切时,圆心距等于两圆半径的和,
故两圆外切.
故选:C.
相交(切)圆连心线的性质
02
圆是轴对称图形,经过圆心的任意一条直线都是圆的对称轴
经过两圆圆心的直线叫做连心线
连接相交两圆的两个交点的线段
叫做公共弦
已知:⊙O1和⊙O2相交于点A、B.
求证:直线O1O2是AB的垂直平分线.
探究1.如图,两圆相交,连心线O1O2与公共弦AB有怎样的关系?
你能用推理的方法来说明吗?
相交两圆的性质定理
相交两圆的连心线垂直平分公共弦
将图(1)中的⊙O1固定,将⊙O2沿直线O1O2向右(左)移动,当移动到如图外切(内切)时,A、B两点一定重合,这一点就是外切(内切)两圆的切点,由此可知两圆相切时切点在连心线上。
相切两圆的性质定理:
相切两圆的连心线经过切点.
例题1.已知:如图,⊙O1和⊙O2相交于A、B两点,线段O1O2的延长线交⊙O2于点C,CA、CB的延长线分别交⊙O1于点D、E.
求证:AD=BE.
例题2:已知⊙O1、⊙O2相交于点D、E,半径分别为15厘米和20厘米,圆心距O1O2为25厘米,
求两圆的公共弦DE的长。
变式:已知已知⊙O1、⊙O2相交于点D、E,半径分别为15厘米和20厘米,公共弦DE的长为24厘米,求两圆的圆心距O1O2 。
圆心在公共弦的两侧或同侧;
连心线垂直平分公共弦.
感谢观看
27.5 圆与圆的位置关系
第27章 圆与正多边形
教师
xxx
沪教版 九年级第二学期
圆与圆的位置关系
相交(切)圆连心线的性质
01
03
02
CONTANTS
目 录
圆与圆的位置关系
01
生活中常见的圆与圆之间的位置关系
在上面的情景中,你能发现两圆的哪些不同的位置?分别用不同颜色的两圆,尝试在展示板上展示出来.
O
O’
观察⊙O与⊙O’在接近过程中的位置关系?
小组讨论:画出⊙O与⊙O’可能出现的情况
情况一
情况二
O’
O
O’
O
情况三
情况四
O’
O
O’
O
情况五
情况六
O’
O
O’
O
外离
外切
相交
内切
(同心圆)
一种特殊的内含
内含
两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.
外离
内含
两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.
两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切,这个惟一的公共点叫做切点.
外切
内切
两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切,这个惟一的公共点叫做切点.
两个圆有两个公共点时,叫做这两个圆相交.
O
2
O
1
相交
问题:能否从两圆公共点的个数来归纳两圆的位置关系?
答:无交点:
相离
外离
内含
有一个交点:
相切
外切
内切
有两个交点:
相交
结论:在同一平面内任意两圆只存在以上三类五种位置关系.
我们发现,我们研究的都是两个半径不同的圆,如果两圆半径相等,是不是也是这五种位置关系呢?
半径不同
d =R+r
d =R-r
d =0
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
当圆心距和半径满足这些关系时,能否得到相应的位置关系吗?
如果我们把两圆圆心的距离记做d(圆心距),大圆的半径记做R,小圆的半径记做r.
两圆的三类五种位置关系下圆心距和两圆半径的数量关系:
两圆外离
d>R1+R2
两圆外切
d= R1+R2
两圆相交
∣R1-R2∣<d<R1+R2
两圆内切
0<d= ∣R1-R2∣
两圆内含
0≤d<∣R1-R2∣
无交点:
两圆相离
有一个交点:
两圆相切
有两个交点:
两圆相交
1.已知两圆半径分别为6.5cm和3cm,圆心距为3.5cm,则两圆的位置关系是( )
A.相交 B.外切 C.内切 D.内含
【详解】
∵两圆的半径分别为6.5cm和3cm,圆心距为3.5cm,且6.5﹣3=3.5,
∴两圆的位置关系是内切.
故选:C.
练一练
2.两圆的半径分别是3㎝和5㎝,圆心距是8㎝,则两圆位置关系是( )
A.相离 B.相交 C.外切 D.内切
【详解】
解:因为3+5=8,圆心距为8,
由于两圆外切时,圆心距等于两圆半径的和,
故两圆外切.
故选:C.
3.⊙的直径,在延长线上,,若⊙与⊙有公共点,那么⊙的半径的取值范围是______________.
【详解】
解:因为3+5=8,圆心距为8,
由于两圆外切时,圆心距等于两圆半径的和,
故两圆外切.
故选:C.
相交(切)圆连心线的性质
02
圆是轴对称图形,经过圆心的任意一条直线都是圆的对称轴
经过两圆圆心的直线叫做连心线
连接相交两圆的两个交点的线段
叫做公共弦
已知:⊙O1和⊙O2相交于点A、B.
求证:直线O1O2是AB的垂直平分线.
探究1.如图,两圆相交,连心线O1O2与公共弦AB有怎样的关系?
你能用推理的方法来说明吗?
相交两圆的性质定理
相交两圆的连心线垂直平分公共弦
将图(1)中的⊙O1固定,将⊙O2沿直线O1O2向右(左)移动,当移动到如图外切(内切)时,A、B两点一定重合,这一点就是外切(内切)两圆的切点,由此可知两圆相切时切点在连心线上。
相切两圆的性质定理:
相切两圆的连心线经过切点.
例题1.已知:如图,⊙O1和⊙O2相交于A、B两点,线段O1O2的延长线交⊙O2于点C,CA、CB的延长线分别交⊙O1于点D、E.
求证:AD=BE.
例题2:已知⊙O1、⊙O2相交于点D、E,半径分别为15厘米和20厘米,圆心距O1O2为25厘米,
求两圆的公共弦DE的长。
变式:已知已知⊙O1、⊙O2相交于点D、E,半径分别为15厘米和20厘米,公共弦DE的长为24厘米,求两圆的圆心距O1O2 。
圆心在公共弦的两侧或同侧;
连心线垂直平分公共弦.
感谢观看
