27.4 直线与圆的位置关系 课件(共32张PPT)
文档属性
| 名称 | 27.4 直线与圆的位置关系 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
27.4 直线与圆的位置关系
第27章 圆与正多边形
教师
xxx
沪教版 九年级第二学期
直线与圆的位置关系
切线的判定
01
02
CONTANTS
目 录
直线与圆的位置关系
01
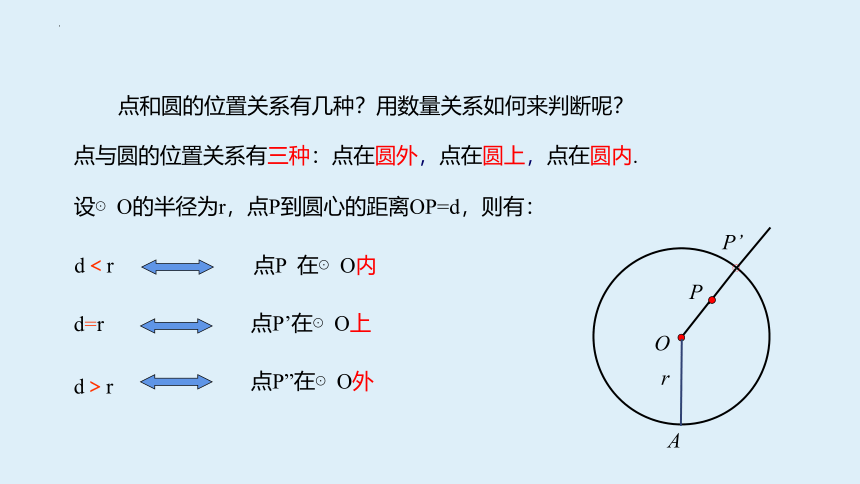
点和圆的位置关系有几种?用数量关系如何来判断呢?
点与圆的位置关系有三种:点在圆外,点在圆上,点在圆内.
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
r
·
O
A
P
P’
d<r
d=r
d>r
点P 在⊙O内
点P’在⊙O上
点P”在⊙O外
思考 (1)在太阳升起的过程中,太阳和海平线会有几种位置关系?如果我们把太阳看作一个圆,把海平线看作一条直线,由此你能得出直线和圆的位置关系吗?
如果从数学的角度来分析,把水面当作一直线,太阳当作一个圆,请同学们利用手中的纸片圆和笔,再现海上日出过程?
再现海上日出过程中,你认为直线和圆有几种位置关系吗?分类依据是什么?
1
2
3
直线l(水面)
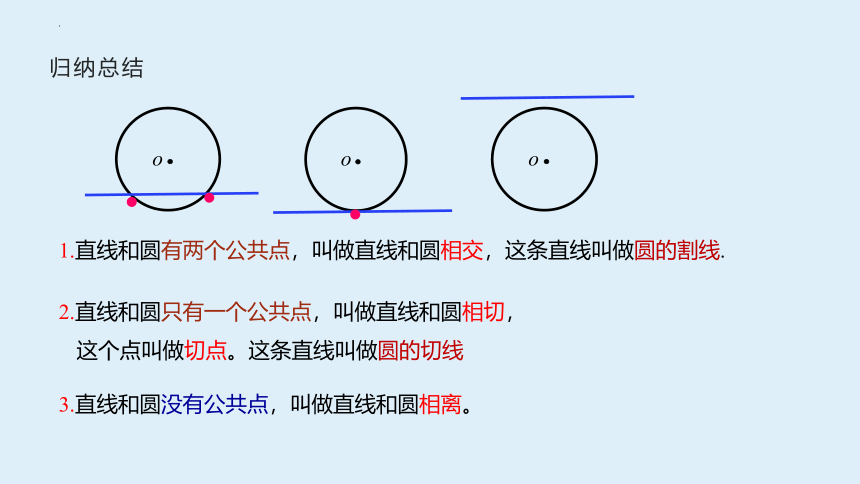
根据直线与圆之间公共点的数量分为以下三类情况:
直线和圆有两个公共点
直线和圆只一个公共点
直线和圆没有公共点
归纳总结
o
o
o
●
●
●
1.直线和圆有两个公共点,叫做直线和圆相交,这条直线叫做圆的割线.
2.直线和圆只有一个公共点,叫做直线和圆相切,
这个点叫做切点。这条直线叫做圆的切线
3.直线和圆没有公共点,叫做直线和圆相离。
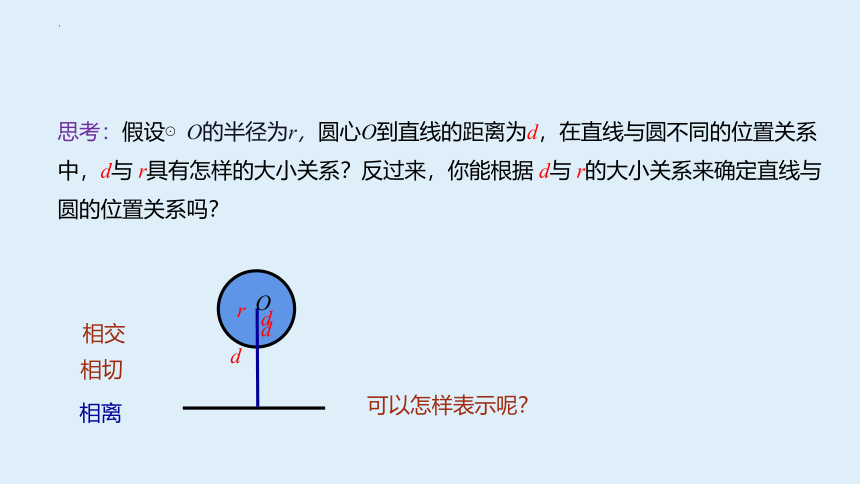
思考:假设⊙O的半径为r,圆心O到直线的距离为d,在直线与圆不同的位置关系中,d与 r具有怎样的大小关系?反过来,你能根据 d与 r的大小关系来确定直线与圆的位置关系吗?
O
d
r
可以怎样表示呢?
相离
相切
相交
d
d
直线l和⊙O相交 d___r;
直线l和⊙O相切 d___r;
直线l和⊙O相离 d___r.
>
<
=
O
l
O
l
O
l
r
d
┐
┐
d
┐
d
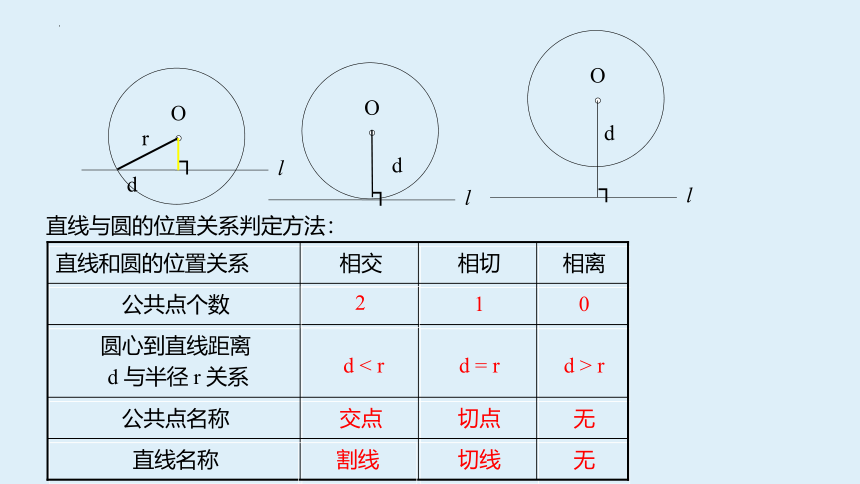
直线与圆的位置关系判定方法:
无
切线
直线名称
无
切点
交点
公共点名称
d > r
d = r
d < r
圆心到直线距离
d 与半径 r 关系
0
1
公共点个数
相离
相切
相交
直线和圆的位置关系
2
割线
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
位置关系
数量关系
公共点个数
2个
1个
0个
例1.直线L与半径为r的⊙O相交,且点O到直线L的距离为6 ,则r的取值范围是__________.
r>6
r=6
变式1-1.直线L与半径为r的⊙O相切,且点O到直线L的距离为6 ,则r的取值范围是__________.
变式1-2.直线L与半径为r的⊙O相离,且点O到直线L的距离为6 ,则r的取值范围是__________.
r<6
变式1-3.如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
【详解】
解:如图,连接OA,作直径MN⊥AB,垂足为D,
由垂径定理可知:AD=DB= AB=4(cm),
∵圆的直径为10cm,
∴DA=5cm,
由勾股定理得:OD=3(cm),
∵垂线段最短,半径最大,
∴OP长度范围为:3≤OP≤5(cm)
M
N
D
例2 已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.无法确定
【答案】B
【详解】
∵圆心到直线的距离5cm=5cm,
∴直线和圆相切,
故选B.
变式2-1 在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相离
C.与x轴相离,与y轴相切 D.与x轴相离,与y轴相离
【答案】B
【详解】
∵是以点(2,3)为圆心,2为半径的圆,
则有2=2,3>2,
∴这个圆与x轴相切,与y轴相离.
故选B.
切线的判定
02
切线的判定
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
l
O
A
例1 如图,已知AB为⊙O的直径,点D在AB的延长线上,BD=OB,
点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
因为点C在圆上,所以连接OC,
证明OC⊥CD,而要证OC⊥CD,
只需证△OCD为直角三角形.
导引:
证明:如图,连接OC,BC.
∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴BC= AB=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°. ∴DC是⊙O的切线.
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
例3 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情况均有可能
C
例4 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
证明:过点O作OE⊥AC,垂足为E,连接OD,OA.
∵⊙O与AB相切于点D
∴OD⊥AB
又△ABC为等腰三角形,O是底边BC的中点.
∴AO是∠BAC的平分线
∴OE=OD,即OE是⊙O的半径
∴AC是⊙O的切线.
E
变式4-1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.
O
B
A
C
证明:连接OC.
∵ OA=OB,CA=CB,
∴ OC是等腰△OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
∟
1.
下列命题中,真命题是( )
A.垂直于半径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到某直线的距离等于半径,那么这条直线是圆的切线
D
课堂练习
2.
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
A.50°
B.80°
C.100°
D.130°
D
3.
如图,PA切⊙O于A,PBC是⊙O的割线,如果PB=2,PC=4,则PA的长为( )
A.2 B. C.4 D.
B
4.
如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
A.50 B.52 C.54 D. 56
B
5.
如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则OB的长为( )
A.4
B.4
C.2
D.2
B
6.如图,AB是⊙O的直径,直线l1 , l2是⊙O的切线,A,B是切点.l1,
l2有怎样的位置关系?证明你的结论.
l1∥l2,
证明:∵直线l1,l2是⊙O的切线,
∴l1⊥AB,l2⊥AB,
∴l1∥l2.
7.
如图,△ABC中AB=AC,D是BC边的中点,以点D为圆心的圆与AB相切于点E.求证:AC与⊙D相切.
证明:作DF⊥AC于F,连接AD、DE.
∵AB是⊙D的切线,∴DE⊥AB,
∵AB=AC,D是BC的中点,
∴AD平分∠BAC
又∵DE⊥AB,DF⊥AC,AD=AD,
∴△ADE≌△ADF,∴DF=DE,
∴AC是⊙D的切线.
8.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.求证:PA是⊙O的切线.
证明:如图,连接OA.
∵∠B=60°, ∴∠AOC=2∠B=120°.
∵OA=OC,∴∠OAC=∠OCA=30°.
又AP=AC,∴∠P=∠ACP=30°,
∴∠OAP=∠AOC-∠P=90°.
∴OA⊥PA,∴PA是⊙O的切线.
感谢观看
27.4 直线与圆的位置关系
第27章 圆与正多边形
教师
xxx
沪教版 九年级第二学期
直线与圆的位置关系
切线的判定
01
02
CONTANTS
目 录
直线与圆的位置关系
01
点和圆的位置关系有几种?用数量关系如何来判断呢?
点与圆的位置关系有三种:点在圆外,点在圆上,点在圆内.
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
r
·
O
A
P
P’
d<r
d=r
d>r
点P 在⊙O内
点P’在⊙O上
点P”在⊙O外
思考 (1)在太阳升起的过程中,太阳和海平线会有几种位置关系?如果我们把太阳看作一个圆,把海平线看作一条直线,由此你能得出直线和圆的位置关系吗?
如果从数学的角度来分析,把水面当作一直线,太阳当作一个圆,请同学们利用手中的纸片圆和笔,再现海上日出过程?
再现海上日出过程中,你认为直线和圆有几种位置关系吗?分类依据是什么?
1
2
3
直线l(水面)
根据直线与圆之间公共点的数量分为以下三类情况:
直线和圆有两个公共点
直线和圆只一个公共点
直线和圆没有公共点
归纳总结
o
o
o
●
●
●
1.直线和圆有两个公共点,叫做直线和圆相交,这条直线叫做圆的割线.
2.直线和圆只有一个公共点,叫做直线和圆相切,
这个点叫做切点。这条直线叫做圆的切线
3.直线和圆没有公共点,叫做直线和圆相离。
思考:假设⊙O的半径为r,圆心O到直线的距离为d,在直线与圆不同的位置关系中,d与 r具有怎样的大小关系?反过来,你能根据 d与 r的大小关系来确定直线与圆的位置关系吗?
O
d
r
可以怎样表示呢?
相离
相切
相交
d
d
直线l和⊙O相交 d___r;
直线l和⊙O相切 d___r;
直线l和⊙O相离 d___r.
>
<
=
O
l
O
l
O
l
r
d
┐
┐
d
┐
d
直线与圆的位置关系判定方法:
无
切线
直线名称
无
切点
交点
公共点名称
d > r
d = r
d < r
圆心到直线距离
d 与半径 r 关系
0
1
公共点个数
相离
相切
相交
直线和圆的位置关系
2
割线
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
位置关系
数量关系
公共点个数
2个
1个
0个
例1.直线L与半径为r的⊙O相交,且点O到直线L的距离为6 ,则r的取值范围是__________.
r>6
r=6
变式1-1.直线L与半径为r的⊙O相切,且点O到直线L的距离为6 ,则r的取值范围是__________.
变式1-2.直线L与半径为r的⊙O相离,且点O到直线L的距离为6 ,则r的取值范围是__________.
r<6
变式1-3.如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
【详解】
解:如图,连接OA,作直径MN⊥AB,垂足为D,
由垂径定理可知:AD=DB= AB=4(cm),
∵圆的直径为10cm,
∴DA=5cm,
由勾股定理得:OD=3(cm),
∵垂线段最短,半径最大,
∴OP长度范围为:3≤OP≤5(cm)
M
N
D
例2 已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.无法确定
【答案】B
【详解】
∵圆心到直线的距离5cm=5cm,
∴直线和圆相切,
故选B.
变式2-1 在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相离
C.与x轴相离,与y轴相切 D.与x轴相离,与y轴相离
【答案】B
【详解】
∵是以点(2,3)为圆心,2为半径的圆,
则有2=2,3>2,
∴这个圆与x轴相切,与y轴相离.
故选B.
切线的判定
02
切线的判定
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
l
O
A
例1 如图,已知AB为⊙O的直径,点D在AB的延长线上,BD=OB,
点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
因为点C在圆上,所以连接OC,
证明OC⊥CD,而要证OC⊥CD,
只需证△OCD为直角三角形.
导引:
证明:如图,连接OC,BC.
∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴BC= AB=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°. ∴DC是⊙O的切线.
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
例3 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情况均有可能
C
例4 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
证明:过点O作OE⊥AC,垂足为E,连接OD,OA.
∵⊙O与AB相切于点D
∴OD⊥AB
又△ABC为等腰三角形,O是底边BC的中点.
∴AO是∠BAC的平分线
∴OE=OD,即OE是⊙O的半径
∴AC是⊙O的切线.
E
变式4-1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.
O
B
A
C
证明:连接OC.
∵ OA=OB,CA=CB,
∴ OC是等腰△OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
∟
1.
下列命题中,真命题是( )
A.垂直于半径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到某直线的距离等于半径,那么这条直线是圆的切线
D
课堂练习
2.
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
A.50°
B.80°
C.100°
D.130°
D
3.
如图,PA切⊙O于A,PBC是⊙O的割线,如果PB=2,PC=4,则PA的长为( )
A.2 B. C.4 D.
B
4.
如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
A.50 B.52 C.54 D. 56
B
5.
如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则OB的长为( )
A.4
B.4
C.2
D.2
B
6.如图,AB是⊙O的直径,直线l1 , l2是⊙O的切线,A,B是切点.l1,
l2有怎样的位置关系?证明你的结论.
l1∥l2,
证明:∵直线l1,l2是⊙O的切线,
∴l1⊥AB,l2⊥AB,
∴l1∥l2.
7.
如图,△ABC中AB=AC,D是BC边的中点,以点D为圆心的圆与AB相切于点E.求证:AC与⊙D相切.
证明:作DF⊥AC于F,连接AD、DE.
∵AB是⊙D的切线,∴DE⊥AB,
∵AB=AC,D是BC的中点,
∴AD平分∠BAC
又∵DE⊥AB,DF⊥AC,AD=AD,
∴△ADE≌△ADF,∴DF=DE,
∴AC是⊙D的切线.
8.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.求证:PA是⊙O的切线.
证明:如图,连接OA.
∵∠B=60°, ∴∠AOC=2∠B=120°.
∵OA=OC,∴∠OAC=∠OCA=30°.
又AP=AC,∴∠P=∠ACP=30°,
∴∠OAP=∠AOC-∠P=90°.
∴OA⊥PA,∴PA是⊙O的切线.
感谢观看
