2014-2015学年高中数学+2-3-1,2-3-2幂函数的概念幂函数的图象和性质课件湘教版必修1(共33张PPT)
文档属性
| 名称 | 2014-2015学年高中数学+2-3-1,2-3-2幂函数的概念幂函数的图象和性质课件湘教版必修1(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-03 21:39:13 | ||
图片预览











文档简介
课件33张PPT。【课标要求】
2.3 幂函数2.3.1 幂函数的概念2.3.2 幂函数的图象和性质一般来说,当x为自变量而α为非0实数时,函数y=xα叫作
(α次的)_________(power fun_ction).
一般说来,我们只考虑定义域为[0,+∞)的分数次幂函数
______,这里p是不为0的整数,q是大于1的正整数,并且p和q_____.
正整数次幂函数的倒数_____,叫作负整数次的幂函数.
一般写成________ ,这里n是正整数,x≠0.
自学导引1.幂函数互素y=x-n负整数次的幂函数和正整数次的幂函数,统称为________
_________.
幂函数:
代表了幂函数的各种不同类型.
对于一般的非0实数α,幂函数y=xα只在______时才能都有意义.对于整数次的幂函数,由于图象的对称性,把它们在__________上的图象和性质说清楚了,其他部分的情形也就很容易了解.
2.3.整数次x>0(0,+∞)的幂函数注意到当x>0时,有等式xα=(eln x)α=_____,可见幂函数
的性质都可以归结到指数函数和对数函数的性质.例如,
由ex和ln x的递增性立刻得知:α>0时xα _____ ;α<0时,xa
_____ ,由ex恒为正可知x>0时_____ .
定义在非负数范围内的幂函数y=xα的定义域只有两种可能:
当α>0时是__________ ,当α<0时是__________ .
(1)当α>0时,幂函数在区间[0,+∞)上有如下性质:
①都经过两个点______和______,即0α=0,1α=1;
②是递___函数;
③图象与直线y=x有如下关系:
4.5.eαlnx递增递减xα>0[0,+∞)(0,+∞)(0,0)(1,1)增在y=x下方在y=x上方在y=x上方在y=x下方(2)当α<0时,幂函数在区间(0,+∞)上有如下性质:
①图象都过点_______,即1α=1;
②是递___函数;
③图象向上与____正向无限接近,向右与____正向无限接近.
(1,1)减y轴x轴y=1和y=x0(x≠0)一样吗?它们都是幂函数吗?
提示 不一样,y=1不是幂函数,y=x0(x≠0)是幂函数.
幂函数与指数函数有什么区别?
提示 指数函数y=ax(a>0且a≠1)的底数a为常数,指数为变量;幂函数y=xα(α∈R)以幂的底为自变量,指数α为常数.
自主探究1.2.答案 C
预习测评A.h(x)C.g(x)答案 D
当x∈(0,1)时,y=xp (p∈R)的图象在y=x的上方,则p的范围是________.
答案 (-∞,1)
已知函数y=(a2-3a+3)xa(a为常数)为幂函数,则a=________.
解析 由幂函数定义知a2-3a+3=1,解得a=1或2.
答案 1或23.4.幂函数
(1)幂函数的有关概念与性质
①幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数.y=x+1,y=x2-2x等都不是幂函数.②在(0,1)上,幂函数中指数愈大,函数图象愈靠近x轴(简记为“指大图低”),在(1,+∞)上,幂函数中指数越大,函数图象越远离x轴.③幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限,至于是否出现在第二、三象限内,要看函数的奇偶性;
名师点睛幂函数的图象最多只能同时出现在两个象限内;
如果幂函数图象与坐标轴相交,则交点一定是原点.
(2)幂函数的图象
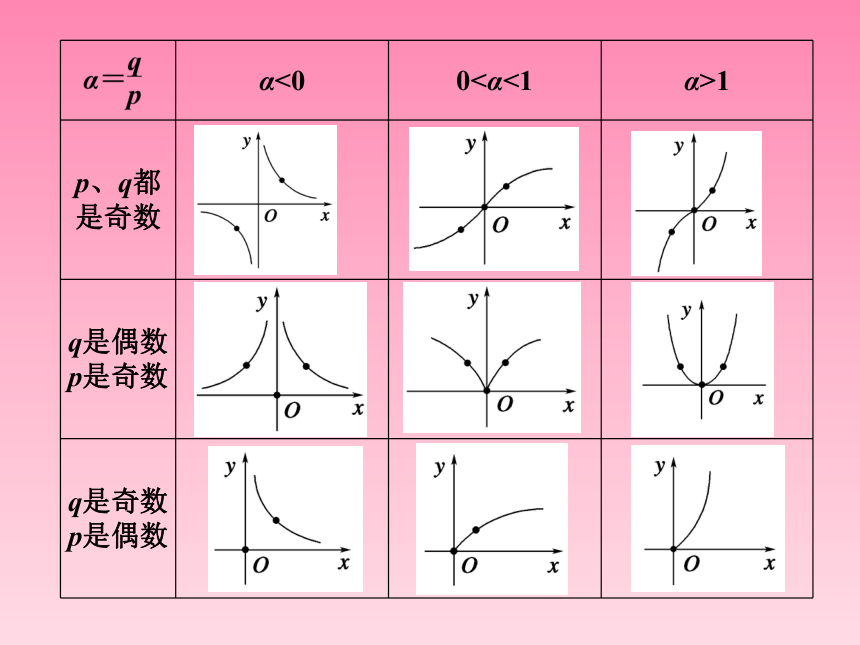
当指数α=1时,y=x的图象是直线;当α=0时,y=xα=x0=1是直线(不包括(0,1)点).除上述特例外,幂函数的图象都是曲线,如下表.
当α>0时,幂函数的图象都经过原点和点(1,1),在第一象限内,当0<α<1时,曲线上凸;当α>1时,曲线下凸.
(3)幂函数的增减性
在区间(0,+∞)上,当α>0时,y=xα是递增函数;当α<0时,y=xα是递减函数.
(4)幂函数的奇偶性
已知函数f(x)=(m2+2m)·xm2+m-1,m为何值时,f(x)是(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.
题型一 幂函数的概念【例1】典例剖析【变式1】题型二 求定义域和值域
【例2】点评 课本上仅研究了几种最简单的幂函数,对于其它幂函数,我们可以利用课本上介绍的方法去研究.对于分数指数的幂函数,我们可以转换成为根式表示的函数再研究.
【变式2】答案 B
题型三 图象问题【例3】答案 D
点评 函数的奇偶性是解答本题的关键所在,在解题过程中要充分利用.
【变式3】答案 D
(2)解 y=x-2定义域为(-∞,0)∪(0,+∞),值域为(0,+∞),是偶函数,且在(0,+∞)上是递减函数,根据以上特征知y=x-2的图象如右图.
题型四 利用幂函数的增减性比较大小【例4】点评 比较大小时,要综合考虑函数的性质,特别是增减性的应用,要善于运用“搭桥”法进行分组,常数0和1是常用的参数.
【变式4】 若(a+1)-1<(3-2a)-1,求实数a的取值范围.
误区警示 因对幂函数的单调性理解不透而出错
【例5】错因分析 函数f(x)=x-1在(-∞,0)和(0,+∞)上均为减函数,但在(-∞,0)∪(0,+∞)上不具有单调性,错解中错用了函数单调性,从而导致错误.
纠错心得 函数的单调性是函数的重要性质,运用单调性时可结合函数的图象进行.幂函数y=x-1的单调性很容易出错,要正确运用.
本节的幂函数不同于其他几种初等函数,虽然形式只有一种:y=xα,但随α值的不同所产生的多种幂函数,在性质、图象方面有一些差异,所以幂函数的知识比较繁琐,须把握规律,加强理解和记忆.
幂函数y=xα与指数函数y=ax(a>0,a≠1)在形式上有相近的地方,但有本质的不同.
(1)幂函数的自变量是底数,指数函数的自变量是指数.
(2)指数函数是整个定义域上的单调函数,但幂函数却不一定.
(3)有些幂函数有奇偶性,但所有的指数函数都不具有奇偶性.
课堂总结1.2.应用幂函数的性质可以比较两个数的大小,当不便直接利用增减性时,可以找到0与1或其他中间数,这种方法可以称为“搭桥”法,另外比较两个函数值的大小还可以借助于图象法或作差法.
3.
2.3 幂函数2.3.1 幂函数的概念2.3.2 幂函数的图象和性质一般来说,当x为自变量而α为非0实数时,函数y=xα叫作
(α次的)_________(power fun_ction).
一般说来,我们只考虑定义域为[0,+∞)的分数次幂函数
______,这里p是不为0的整数,q是大于1的正整数,并且p和q_____.
正整数次幂函数的倒数_____,叫作负整数次的幂函数.
一般写成________ ,这里n是正整数,x≠0.
自学导引1.幂函数互素y=x-n负整数次的幂函数和正整数次的幂函数,统称为________
_________.
幂函数:
代表了幂函数的各种不同类型.
对于一般的非0实数α,幂函数y=xα只在______时才能都有意义.对于整数次的幂函数,由于图象的对称性,把它们在__________上的图象和性质说清楚了,其他部分的情形也就很容易了解.
2.3.整数次x>0(0,+∞)的幂函数注意到当x>0时,有等式xα=(eln x)α=_____,可见幂函数
的性质都可以归结到指数函数和对数函数的性质.例如,
由ex和ln x的递增性立刻得知:α>0时xα _____ ;α<0时,xa
_____ ,由ex恒为正可知x>0时_____ .
定义在非负数范围内的幂函数y=xα的定义域只有两种可能:
当α>0时是__________ ,当α<0时是__________ .
(1)当α>0时,幂函数在区间[0,+∞)上有如下性质:
①都经过两个点______和______,即0α=0,1α=1;
②是递___函数;
③图象与直线y=x有如下关系:
4.5.eαlnx递增递减xα>0[0,+∞)(0,+∞)(0,0)(1,1)增在y=x下方在y=x上方在y=x上方在y=x下方(2)当α<0时,幂函数在区间(0,+∞)上有如下性质:
①图象都过点_______,即1α=1;
②是递___函数;
③图象向上与____正向无限接近,向右与____正向无限接近.
(1,1)减y轴x轴y=1和y=x0(x≠0)一样吗?它们都是幂函数吗?
提示 不一样,y=1不是幂函数,y=x0(x≠0)是幂函数.
幂函数与指数函数有什么区别?
提示 指数函数y=ax(a>0且a≠1)的底数a为常数,指数为变量;幂函数y=xα(α∈R)以幂的底为自变量,指数α为常数.
自主探究1.2.答案 C
预习测评A.h(x)
当x∈(0,1)时,y=xp (p∈R)的图象在y=x的上方,则p的范围是________.
答案 (-∞,1)
已知函数y=(a2-3a+3)xa(a为常数)为幂函数,则a=________.
解析 由幂函数定义知a2-3a+3=1,解得a=1或2.
答案 1或23.4.幂函数
(1)幂函数的有关概念与性质
①幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数.y=x+1,y=x2-2x等都不是幂函数.②在(0,1)上,幂函数中指数愈大,函数图象愈靠近x轴(简记为“指大图低”),在(1,+∞)上,幂函数中指数越大,函数图象越远离x轴.③幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限,至于是否出现在第二、三象限内,要看函数的奇偶性;
名师点睛幂函数的图象最多只能同时出现在两个象限内;
如果幂函数图象与坐标轴相交,则交点一定是原点.
(2)幂函数的图象
当指数α=1时,y=x的图象是直线;当α=0时,y=xα=x0=1是直线(不包括(0,1)点).除上述特例外,幂函数的图象都是曲线,如下表.
当α>0时,幂函数的图象都经过原点和点(1,1),在第一象限内,当0<α<1时,曲线上凸;当α>1时,曲线下凸.
(3)幂函数的增减性
在区间(0,+∞)上,当α>0时,y=xα是递增函数;当α<0时,y=xα是递减函数.
(4)幂函数的奇偶性
已知函数f(x)=(m2+2m)·xm2+m-1,m为何值时,f(x)是(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.
题型一 幂函数的概念【例1】典例剖析【变式1】题型二 求定义域和值域
【例2】点评 课本上仅研究了几种最简单的幂函数,对于其它幂函数,我们可以利用课本上介绍的方法去研究.对于分数指数的幂函数,我们可以转换成为根式表示的函数再研究.
【变式2】答案 B
题型三 图象问题【例3】答案 D
点评 函数的奇偶性是解答本题的关键所在,在解题过程中要充分利用.
【变式3】答案 D
(2)解 y=x-2定义域为(-∞,0)∪(0,+∞),值域为(0,+∞),是偶函数,且在(0,+∞)上是递减函数,根据以上特征知y=x-2的图象如右图.
题型四 利用幂函数的增减性比较大小【例4】点评 比较大小时,要综合考虑函数的性质,特别是增减性的应用,要善于运用“搭桥”法进行分组,常数0和1是常用的参数.
【变式4】 若(a+1)-1<(3-2a)-1,求实数a的取值范围.
误区警示 因对幂函数的单调性理解不透而出错
【例5】错因分析 函数f(x)=x-1在(-∞,0)和(0,+∞)上均为减函数,但在(-∞,0)∪(0,+∞)上不具有单调性,错解中错用了函数单调性,从而导致错误.
纠错心得 函数的单调性是函数的重要性质,运用单调性时可结合函数的图象进行.幂函数y=x-1的单调性很容易出错,要正确运用.
本节的幂函数不同于其他几种初等函数,虽然形式只有一种:y=xα,但随α值的不同所产生的多种幂函数,在性质、图象方面有一些差异,所以幂函数的知识比较繁琐,须把握规律,加强理解和记忆.
幂函数y=xα与指数函数y=ax(a>0,a≠1)在形式上有相近的地方,但有本质的不同.
(1)幂函数的自变量是底数,指数函数的自变量是指数.
(2)指数函数是整个定义域上的单调函数,但幂函数却不一定.
(3)有些幂函数有奇偶性,但所有的指数函数都不具有奇偶性.
课堂总结1.2.应用幂函数的性质可以比较两个数的大小,当不便直接利用增减性时,可以找到0与1或其他中间数,这种方法可以称为“搭桥”法,另外比较两个函数值的大小还可以借助于图象法或作差法.
3.
