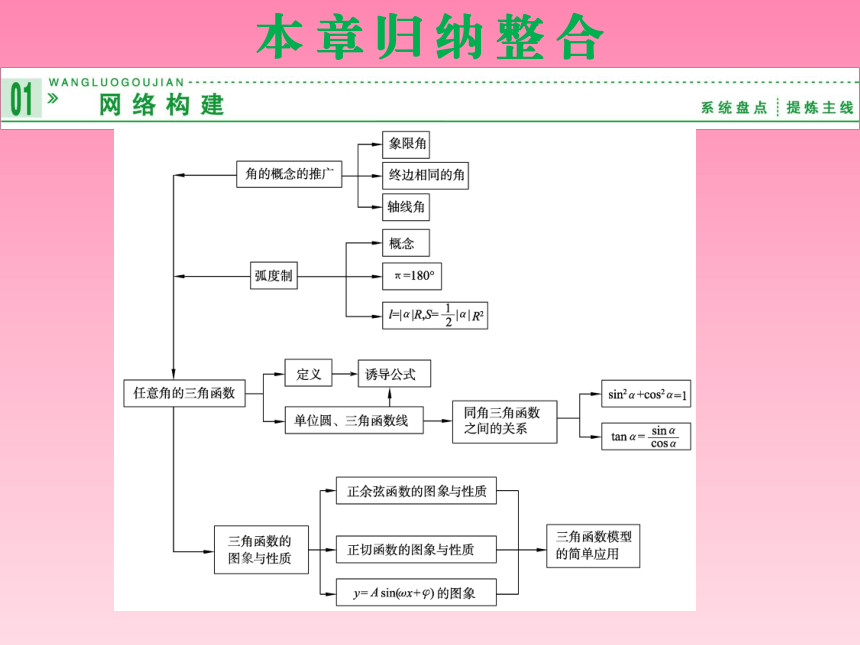
2014-2015学年高中数学本章归纳整合(第三章)课件湘教版必修2(共21张PPT)
文档属性
| 名称 | 2014-2015学年高中数学本章归纳整合(第三章)课件湘教版必修2(共21张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-04 00:00:00 | ||
图片预览



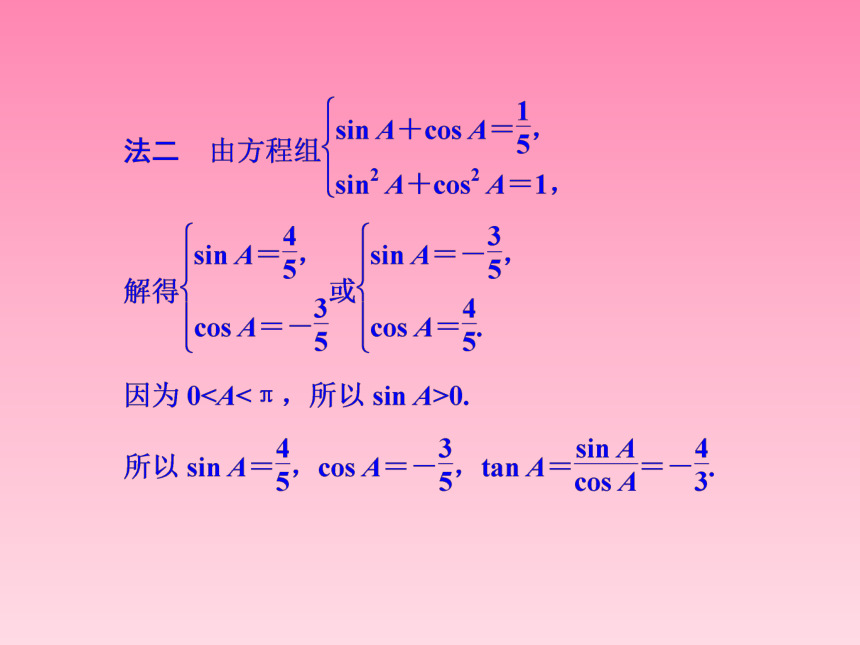

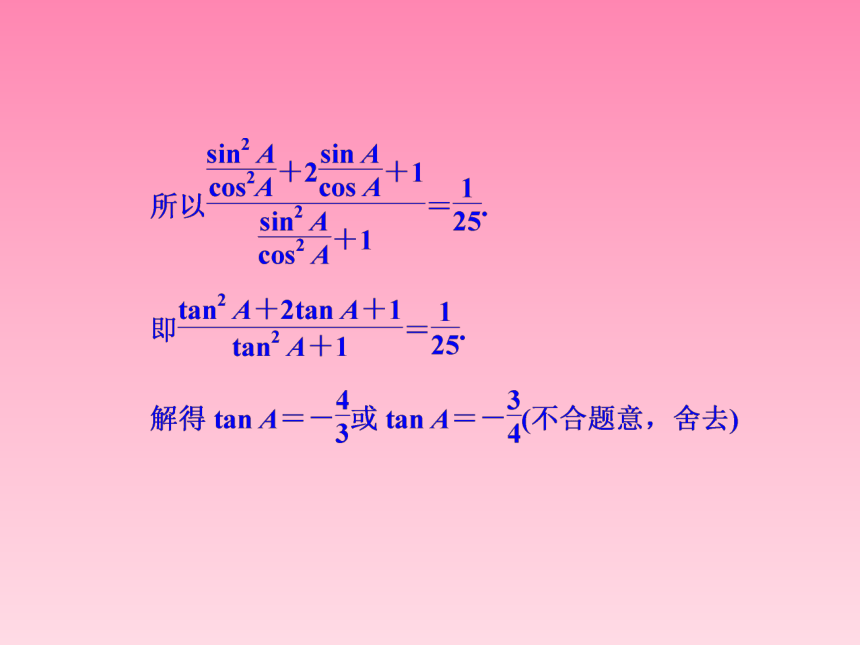

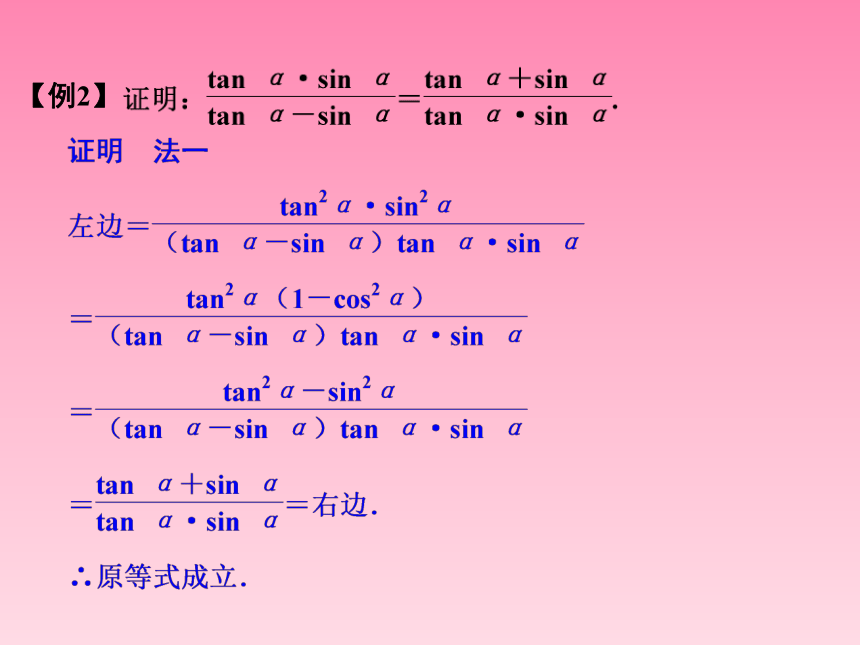

文档简介
课件21张PPT。本 章 归 纳 整 合专题一 三角函数式的化简、求值与证明
利用三角函数的定义、同角基本关系式和诱导公式等,进行三角函数式的化简、求值与证明,是三角变换的基本题型.解答此类问题的基本原则就是“找差异,求统一”,观察函数角之间的关系,函数名称的异同,以及函数式的结构特点,通过角的变换、化切为弦、结构变形等手段,清除差异,取得统一.同时注意分类讨论、整体转化、函数与方程等思想方法在解题中的应用.
已知A是△ABC的内角,且sin A+cos A= ,求tan A的值.
【例1】【例2】点评 三角恒等式的证明,实质上就是有目标的化简.观察等式两边函数角、函数名以及结构形式之间的区别和联系,通过三角变换清除差异,寻求统一.一般原则是由繁到简,如果两边都比较复杂,也可以两边同时化简,如证法二.
三角函数的图象和性质,分别从“形”和“数”这两个不同侧面反映了三角函数的变化规律,充分体现了数形结合的思想方法,是历年高考的重点.主要考查图象变换、由图象确定解析式以及讨论三角函数的有关性质.
专题二 三角函数的图象与性质【例3】(1)求函数f1(x)的表达式;
(2)试说明如何由y=f1(x)的图象变换而得到f2(x)=sin x的图象.
点评 (1)由图象求解析式,应充分利用图象所提供的信息.在五个点中,任知两个点的横坐标,就可确定ω和φ.对于A,如果给出最高点或最低点的纵坐标,则可直接观察得到;如果给出某个点的坐标,则需代入解析式求解.
(2)图象变换一定要注意是伸长还是缩短,是向左还是右,一定要记牢用熟,以免混淆.
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一
条对称轴是直线x= .
(1)求φ;
(2)求函数y=f(x)的单调递增区间;
(3)画出函数y=f(x)在区间[0,π]上的图象.
【例4】故函数y=f(x)在区间[0,π]上的图象如图所示.
三角不等式是指sin(ωx+φ)>a(或a(或a(或专题三 解三角函数不等式 求不等式2sin2x-cos x-1>0的解集.
解 原不等式化为
2(1-cos2x)-cos x-1>0,即2cos2x+cos x-1<0.
【例5】作函数y=cos x,x∈[0,2π]的图象.(如下图).
【例6】
利用三角函数的定义、同角基本关系式和诱导公式等,进行三角函数式的化简、求值与证明,是三角变换的基本题型.解答此类问题的基本原则就是“找差异,求统一”,观察函数角之间的关系,函数名称的异同,以及函数式的结构特点,通过角的变换、化切为弦、结构变形等手段,清除差异,取得统一.同时注意分类讨论、整体转化、函数与方程等思想方法在解题中的应用.
已知A是△ABC的内角,且sin A+cos A= ,求tan A的值.
【例1】【例2】点评 三角恒等式的证明,实质上就是有目标的化简.观察等式两边函数角、函数名以及结构形式之间的区别和联系,通过三角变换清除差异,寻求统一.一般原则是由繁到简,如果两边都比较复杂,也可以两边同时化简,如证法二.
三角函数的图象和性质,分别从“形”和“数”这两个不同侧面反映了三角函数的变化规律,充分体现了数形结合的思想方法,是历年高考的重点.主要考查图象变换、由图象确定解析式以及讨论三角函数的有关性质.
专题二 三角函数的图象与性质【例3】(1)求函数f1(x)的表达式;
(2)试说明如何由y=f1(x)的图象变换而得到f2(x)=sin x的图象.
点评 (1)由图象求解析式,应充分利用图象所提供的信息.在五个点中,任知两个点的横坐标,就可确定ω和φ.对于A,如果给出最高点或最低点的纵坐标,则可直接观察得到;如果给出某个点的坐标,则需代入解析式求解.
(2)图象变换一定要注意是伸长还是缩短,是向左还是右,一定要记牢用熟,以免混淆.
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一
条对称轴是直线x= .
(1)求φ;
(2)求函数y=f(x)的单调递增区间;
(3)画出函数y=f(x)在区间[0,π]上的图象.
【例4】故函数y=f(x)在区间[0,π]上的图象如图所示.
三角不等式是指sin(ωx+φ)>a(或
解 原不等式化为
2(1-cos2x)-cos x-1>0,即2cos2x+cos x-1<0.
【例5】作函数y=cos x,x∈[0,2π]的图象.(如下图).
【例6】
