2014-2015学年高中数学本章归纳整合(第五章)课件湘教版必修2(共19张PPT)
文档属性
| 名称 | 2014-2015学年高中数学本章归纳整合(第五章)课件湘教版必修2(共19张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-03 21:53:18 | ||
图片预览


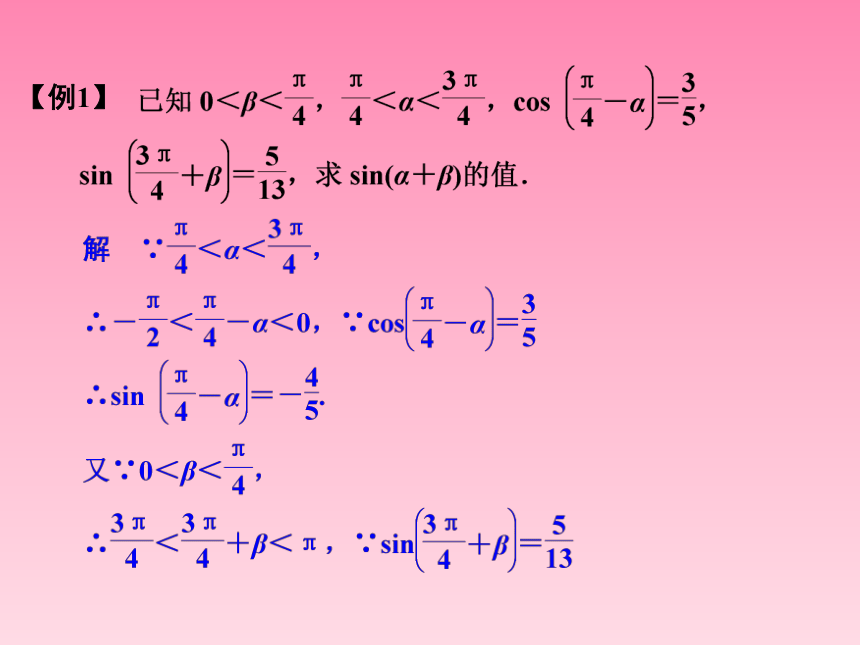

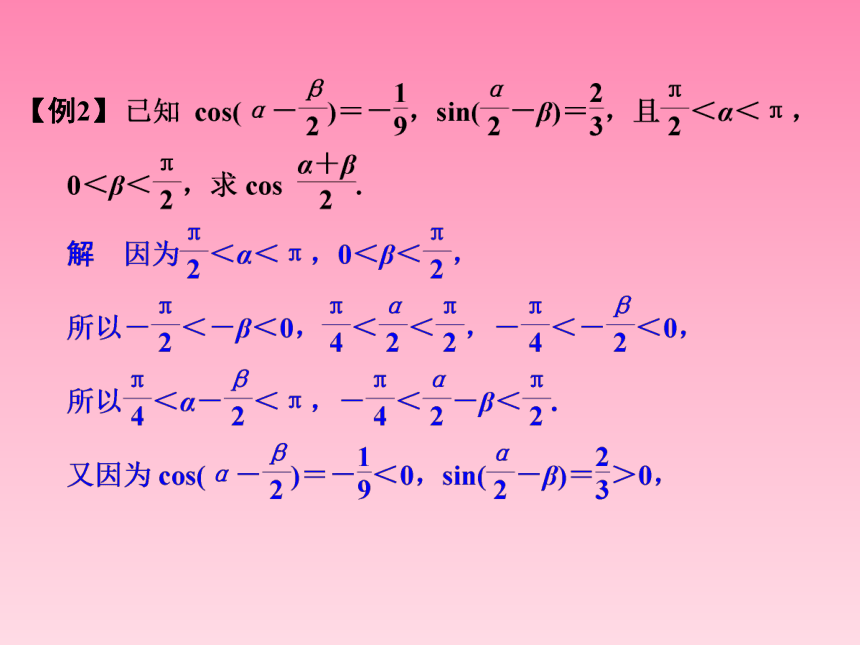


文档简介
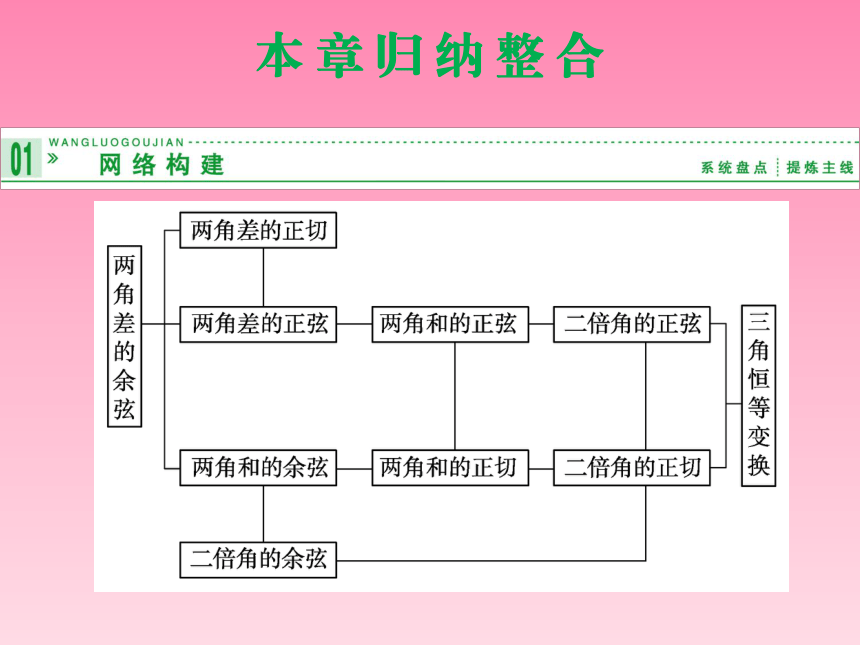
课件19张PPT。本 章 归 纳 整 合专题一 三角变换中的求值问题
三角变换中的求值问题主要有两类,给角求值和给值求值.
给角求值一般是利用和、差、倍公式进行变换,使其出现特殊角,若为非特殊角,则应变为可消去或约分的情况,从而求出其值.
给值求值一般应先化简所求的式子,弄清实际所求,或变化已知的式子,寻找已知与所求的联系,再求值.
【例1】点评 由于已知条件中的角与所求式中的角度不一致,将它们统一起来再变换是解题的关键.
【例2】三角函数式的化简是三角变换应用的一个重要方面,其基本思想方法是统一角,统一三角函数的名称.在具体实施过程中,应着重抓住“角”的统一.通过观察角、函数名、项的次数等,找到突破口,利用切化弦、升幂、降幂、逆用公式等手段将其化简.最后结果应为:(1)能求值尽量求值;(2)三角函数名称尽量少;(3)项数尽量少;(4)次数尽量低;(5)分母、根号下尽量不含三角函数.
专题二 化简三角函数式【例3】点评 化简三角函数式的基本要求是:减少角的种类,使形式尽量简洁.为使形式尽量简洁,要注意,有根号的去根号,异角化同角,异次化同次,能求值的求出值.【例4】点评 1±sin α和1±cos α都可以通过升幂而转化为完全平方式,如果需要开方,则一定要注意角的范围,必要时需进行讨论.
三角恒等式的证明主要有两种类型:绝对恒等式与条件恒等式.
证明绝对恒等式要根据等式两边的特征,采取化繁为简,左右归一,变更命题等方法,通过三角恒等变换,使等式的两边化异为同.
条件恒等式的证明则要认真观察、比较已知条件与求证等式之间的联系,选择适当途径.常用代入法、消去法、两头凑等.
专题三 三角恒等式的证明
已知tan(α+β)=2tan β,求证:3sin α=sin(α+2β).
【例5】∴sin(α+β)·cos β=2cos(α+β)·sin β.
而sin(α+2β)=sin [(α+β)+β]
=sin(α+β)·cos β+cos(α+β)·sin β
=2cos(α+β)·sin β+cos(α+β)·sin β
=3cos(α+β)·sin β.
又sin α=sin [(α+β)-β]
=sin(α+β)·cos β-cos(α+β)·sin β
=2cos(α+β)·sin β-cos(α+β)·sin β
=cos(α+β)·sin β.
故sin(α+2β)=3sin α.
点评 三角式的化简或证明,主要从三方面寻求思路:一是观察函数特点,已知和所求中包含什么函数,它们可以怎样联系;二是观察角的特点,它们之间可经过何种形式联系起来;三是观察结构特点,它们之间经过怎样的变形可达到统一.
【例6】专题四 三角变换的综合应用【例7】点评 本题是与向量结合的综合题,解题时,应先利用向量模及数量积的坐标运算,找出α所满足的关系式,再化简求值即可.
【例8】
三角变换中的求值问题主要有两类,给角求值和给值求值.
给角求值一般是利用和、差、倍公式进行变换,使其出现特殊角,若为非特殊角,则应变为可消去或约分的情况,从而求出其值.
给值求值一般应先化简所求的式子,弄清实际所求,或变化已知的式子,寻找已知与所求的联系,再求值.
【例1】点评 由于已知条件中的角与所求式中的角度不一致,将它们统一起来再变换是解题的关键.
【例2】三角函数式的化简是三角变换应用的一个重要方面,其基本思想方法是统一角,统一三角函数的名称.在具体实施过程中,应着重抓住“角”的统一.通过观察角、函数名、项的次数等,找到突破口,利用切化弦、升幂、降幂、逆用公式等手段将其化简.最后结果应为:(1)能求值尽量求值;(2)三角函数名称尽量少;(3)项数尽量少;(4)次数尽量低;(5)分母、根号下尽量不含三角函数.
专题二 化简三角函数式【例3】点评 化简三角函数式的基本要求是:减少角的种类,使形式尽量简洁.为使形式尽量简洁,要注意,有根号的去根号,异角化同角,异次化同次,能求值的求出值.【例4】点评 1±sin α和1±cos α都可以通过升幂而转化为完全平方式,如果需要开方,则一定要注意角的范围,必要时需进行讨论.
三角恒等式的证明主要有两种类型:绝对恒等式与条件恒等式.
证明绝对恒等式要根据等式两边的特征,采取化繁为简,左右归一,变更命题等方法,通过三角恒等变换,使等式的两边化异为同.
条件恒等式的证明则要认真观察、比较已知条件与求证等式之间的联系,选择适当途径.常用代入法、消去法、两头凑等.
专题三 三角恒等式的证明
已知tan(α+β)=2tan β,求证:3sin α=sin(α+2β).
【例5】∴sin(α+β)·cos β=2cos(α+β)·sin β.
而sin(α+2β)=sin [(α+β)+β]
=sin(α+β)·cos β+cos(α+β)·sin β
=2cos(α+β)·sin β+cos(α+β)·sin β
=3cos(α+β)·sin β.
又sin α=sin [(α+β)-β]
=sin(α+β)·cos β-cos(α+β)·sin β
=2cos(α+β)·sin β-cos(α+β)·sin β
=cos(α+β)·sin β.
故sin(α+2β)=3sin α.
点评 三角式的化简或证明,主要从三方面寻求思路:一是观察函数特点,已知和所求中包含什么函数,它们可以怎样联系;二是观察角的特点,它们之间可经过何种形式联系起来;三是观察结构特点,它们之间经过怎样的变形可达到统一.
【例6】专题四 三角变换的综合应用【例7】点评 本题是与向量结合的综合题,解题时,应先利用向量模及数量积的坐标运算,找出α所满足的关系式,再化简求值即可.
【例8】
