2023-2024学年山东省滨州市惠民县高二(上)期中数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年山东省滨州市惠民县高二(上)期中数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 218.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:21:24 | ||
图片预览




文档简介
2023-2024学年山东省滨州市惠民县高二(上)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.直线的倾斜角( )
A. B. C. D.
2.圆的圆心坐标为( )
A. B. C. D.
3.设是正三棱锥,是的重心,是上的一点,且,若,则( )
A. B. C. D.
4.万众瞩目的北京冬奥会将于年月日正式开幕,继年北京奥运会之后,国家体育场又名鸟巢将再次承办奥运会开幕式.在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同,扁平程度相同的椭圆,已知大椭圆的长轴长为,短轴长为,小椭圆的短轴长为,则小椭圆的长轴长为.( )
A. B. C. D.
5.已知点,,点在圆上,则的面积的最小值为( )
A. B. C. D.
6.如图,过抛物线的焦点的直线交抛物线于点,,交其准线于点,准线与对称轴交于点,若,且,则为( )
A.
B.
C.
D.
7.设是圆:上的一动点,定点,线段的垂直平分线交线段于点,则点的轨迹方程为( )
A. B. C. D.
8.如图,在正方体中,是中点,点在线段上,若直线与平面所成的角为,则的取值范围是( )
A.
B.
C.
D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.点到直线,的距离可能是( )
A. B. C. D.
10.关于空间向量,以下说法正确的是( )
A. 空间中的三个向量,若有两个向量共线,则这三个向量一定共面
B. 若对空间中任意一点,有,则,,,四点共面
C. 设是空间中的一组基底,则也是空间的一组基底
D. 若,则,是钝角
11.如图所示,正方体的棱长为,线段上有两个动点,且,则下列结论中正确的是( )
A.
B. 平面
C. 三棱锥的体积为定值
D. 异面直线,所成的角为定值
12.已知椭圆:,为的左焦点,直线与交于,两点点在第一象限,直线与椭圆的另一个交点为,则( )
A. B. 当时,的面积为
C. D. 的周长的最大值为
三、填空题:本题共4小题,每小题5分,共20分。
13.若直线:与直线:平行,则直线与之间的距离为______ .
14.已知是不共面向量,,若三个向量共面,则实数 ______ .
15.已知点在圆的外部,则的取值范围是______ .
16.椭圆的光学性质,从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上.已知椭圆:,,为其左、右焦点.是上的动点,点,若的最大值为动直线为此椭圆的切线,右焦点关于直线的对称点,,则:
椭圆的离心率为______;
的取值范围为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
直线经过两直线:和:的交点.
若直线与直线垂直,求直线的方程;
若点到直线的距离为,求直线的方程.
18.本小题分
已知直线和圆.
若直线交圆于,两点,求弦的长;
求过点且与圆相切的直线方程.
19.本小题分
如图所示,在直三棱柱中,,,,.
求证:;
在上是否存在点,使得平面,若存在,确定点位置并说明理由,若不存在,说明理由.
20.本小题分
平面直角坐标系中,点到点的距离比它到轴的距离多,记点的轨迹为.
求轨迹的方程;
设斜率为的直线过定点,若直线与轨迹恰好有一个公共点,求实数的取值范围.
21.本小题分
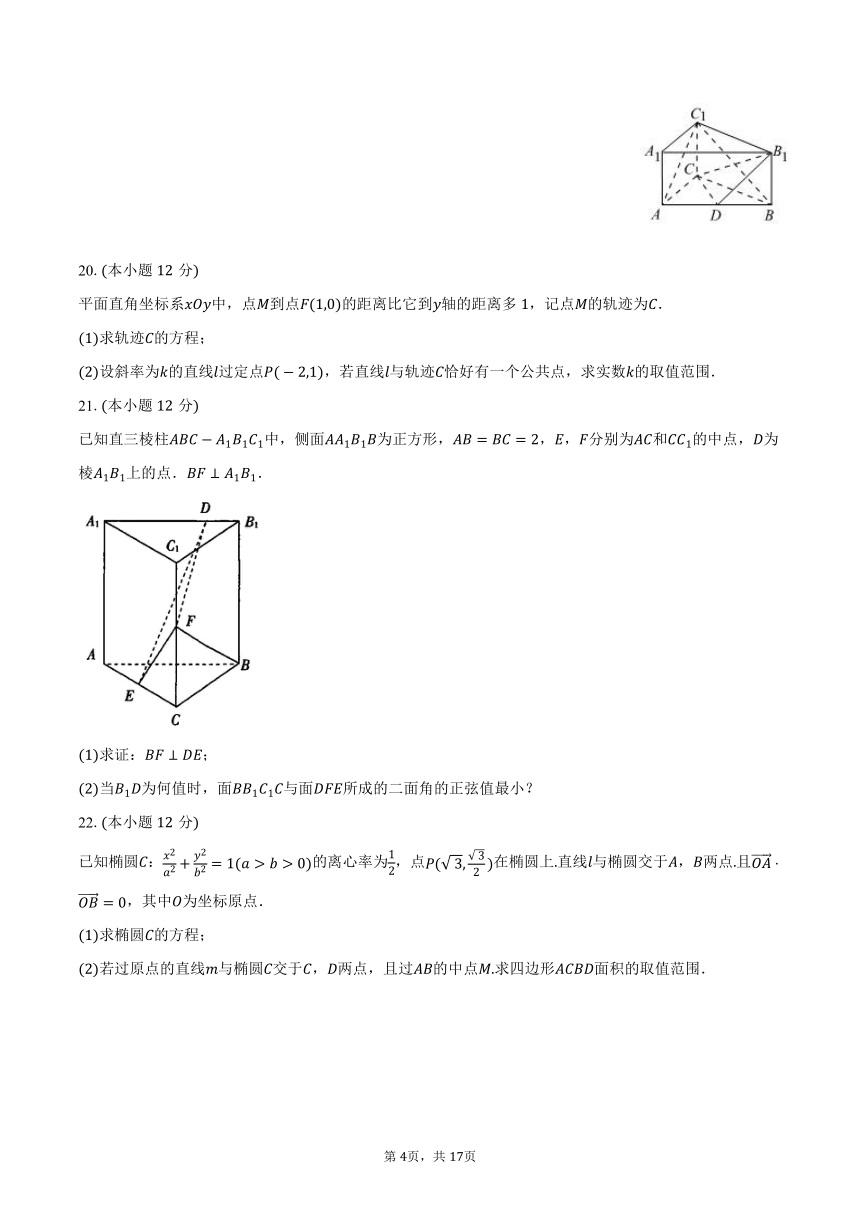
已知直三棱柱中,侧面为正方形,,,分别为和的中点,为棱上的点..
求证:;
当为何值时,面与面所成的二面角的正弦值最小?
22.本小题分
已知椭圆:的离心率为,点在椭圆上直线与椭圆交于,两点且,其中为坐标原点.
求椭圆的方程;
若过原点的直线与椭圆交于,两点,且过的中点求四边形面积的取值范围.
答案和解析
1.【答案】
【解析】解:由题意可得直线的斜率为,
直线倾斜角为,,则,故.
故选:.
确定直线的斜率,根据斜率与倾斜角的关系,即可求得答案.
本题主要考查直线的倾斜角,属于基础题.
2.【答案】
【解析】解:圆即,
所以圆心坐标为.
故选:.
将圆的方程配成标准式,即可得解.
本题主要考查圆的一般方程,属于基础题.
3.【答案】
【解析】【分析】
本题考查了平面向量基本定理的应用,涉及到三角形重心的性质以及中线的性质,属于基础题.
先取的中点,然后利用三角形法则以及三角形重心的性质和中线的性质即可求解.
【解答】
解:如图所示:
取的中点,连接,
因为是的重心,
所以在上,
因为,
所以
,
所以,
故选:.
4.【答案】
【解析】【分析】
求出大椭圆的离心率等于小椭圆的离心率,然后求解小椭圆的长轴长.
本题考查椭圆的简单性质的应用,是基本知识的考查.
【解答】
解:因为两个椭圆的扁平程度相同,所以椭圆的离心率相同,
所以两个椭圆的离心率相同,
所以,
所以,
所以小椭圆的长轴长为:.
故选:.
5.【答案】
【解析】解:圆的圆心,半径为
,,则,直线:,
圆心到直线的距离,
的面积最小时,点到直线的距离最短,该最短距离即圆心到直线的距离减去圆的半径,
边上高的最小值为,则的最小值为,
故选:.
首先求出直线的方程和线段的长度,利用圆心到直线的距离再减去圆的半径得出的高的最小值,即可求解.
本题主要考查直线和圆的位置关系,属于中档题.
6.【答案】
【解析】解:如图,分别过点、作准线的垂线,垂足分别为点、,
设,则由已知得,由抛物线的定义得,
故,
在直角三角形中,,,
又因为,
则,从而得,
又因为,
所以.
故选:.
分别过点、作准线的垂线,垂足分别为点、,设,根据抛物线的定义以及图象可得,结合已知条件求得,,即可.
本题考查抛物线的几何性质,属中档题.
7.【答案】
【解析】解:线段是线段的垂直平分线交线,
,,
,
,,即点是到定点,距离和为定长的动点,
点的轨迹为椭圆,,,则,
点的轨迹方程为:.
故选:.
利用垂直平分线性质得到,由几何线段的关系得到,根据椭圆的定义即可写出点的轨迹方程.
本题主要考查了轨迹方程的问题,解题的关键是利用了椭圆的定义求得轨迹方程.
8.【答案】
【解析】解:设正方体边长为,.
以为原点,分别以,,为坐标轴建立空间直角坐标系,
则,,,
易证平面,
是平面的一个法向量.
,,
当时取得最大值,当或时,取得最小值.
故选:.
设,以为原点建立坐标系,则是平面的一个法向量.的坐标,得出,关于的函数,根据二次函数的性质得出的取值范围.
本题考查了空间向量与线面角的计算,属于中档题.
9.【答案】
【解析】解:对于直线,,
令,解得,
故直线的必过点为,
设点到直线,的距离为,
则,
所以,,而,
所以,ABC正确,D错误.
故选:.
求出直线的必过点,利用两点间距离公式求出的最大值,进而得到的范围.
本题考查直线的定点以及两点间的距离公式的运用,考查运算求解能力,属于基础题.
10.【答案】
【解析】【分析】
本题考查了空间向量的共线定理,共面定理的应用,考查了基底的概念以及向量的夹角的应用,属于中档题.
根据向量共线的概念即可判断选项A;根据空间向量的基本定理即可判断选项B;根据空间向量的基底的概念即可判断选项C;根据向量夹角的定义即可判断选项D.
【解答】
解:选项A:根据共线向量的概念,可知空间中的三个向量,
若有两个向量共线,则这三个向量一定共面,故A正确;
选项B:因为对空间中任意一点,有,
则,整理可得:,
由平面向量基本定理可知点,,,四点一定共面,故B正确;
选项C:由是空间中的一组基底,则向量不共面,
可得向量也不共面,所以也是空间中的一组基底,故C正确;
选项D:若,则为钝角或,故D错误.
故选:.
11.【答案】
【解析】解:平面,又平面,
,故A正确;
平面,又、在直线上运动,
平面,故B正确;
由于点到直线的距离不变,故的面积为定值.
又点到平面的距离为,故为定值,C正确;
当点在处,为的中点时,异面直线,所成的角是,
当在上底面的中心时,在的位置,异面直线,所成的角是,
显然两个角不相等,不正确.
故选:.
通过直线垂直平面平面,判断是正确的;通过直线平行直线,判断平面,是正确的;计算三角形的面积和到平面的距离是定值,说明是正确的;只需找出两个特殊位置,即可判断是不正确的.
本题考查直线与平面平行的判定,棱锥的体积,异面直线及其所成的角,考查空间想象能力,是中档题.
12.【答案】
【解析】解:椭圆:,所以,,所以,所以A正确;
为的左焦点,直线与交于,两点点在第一象限,直线与椭圆的另一个交点为,
当时,的面积为:,所以不正确;
直线与椭圆的另一个交点为,,的参数方程为:,代入椭圆方程化简可得:,
设,,.
所以C正确;
的周长的最大值为,所以不正确;
故选:.
利用已知条件求解椭圆的离心率,判断;求解三角形的面积判断;利用直线与椭圆的位置关系,转化求解判断,结合椭圆的定义,判断即可.
本题考查直线与椭圆的位置关系的综合应用,椭圆的简单性质的应用,是中档题.
13.【答案】
【解析】解:因为,
所以,解得,
所以直线的方程为,
直线的方程为,即,
所以直线与之间的距离为.
故答案为:.
先求得的值,然后根据两条平行直线间的距离公式求得正确答案.
本题考查平行线距离公式,属于基础题.
14.【答案】
【解析】解:以为空间一组基底,
由于三个向量共面,所以存在,,
使得,
即,
整理得,
所以,解得.
故答案为:.
根据向量共面列方程,化简求得的值.
本题考查向量的共面定理相关知识,属于基础题.
15.【答案】
【解析】解:圆,即,
,即.
点在圆的外部,,.
综上可得,,
故答案为:.
根据圆的标准方程的特征可得,再根据点在圆的外部可得,综合可得实数的取值范围.
本题主要考查圆的标准方程、点和圆的位置关系,属于基础题.
16.【答案】
【解析】解:根据椭圆定义,得,
所以,
因为的最大值为,
因为,所以,即,解得,
所以离心率为;
右焦点关于直线的对称点,
设切点为,由椭圆的光学性质,可得,,三点共线,
所以,
即点的轨迹是以为圆心,半径为的圆,
圆心到直线的距离为,
则圆上的点到直线的距离最小值,最大值,
所以点到直线的距离为,
所以表示点到直线的距离的倍,
则,即.
故答案为:.
根据题意得,所以,求出,即可求出,再求出离心率;根据椭圆的光学性质可得,即点的轨迹是以为圆心,半径为的圆,又表示点到直线的距离的倍,再求出的范围.
本题考查了椭圆的几何性质,与圆有关的最值问题,属于中档题.
17.【答案】解:联立方程组,
解得,
所以交点坐标为,
又因为直线与直线垂直,所以直线的斜率为,
则直线的方程为,即;
当直线的斜率不存在时,直线的方程为,满足点到直线的距离为;
当直线的斜率存在时,设直线的方程为,即,
则点到直线的距离为,
解得,
故直线的方程为,即,
综上可得,直线的方程为或.
【解析】联立方程组,求得两直线的交点坐标,利用垂直关系求得斜率,结合点斜式方程,即可求解;
分直线的斜率存在与不存在,结合点到直线的距离公式求得斜率,利用点斜式方程,即可求解.
本题主要考查了求直线的一般方程,考查了两直线垂直时的斜率关系,以及点到直线的距离公式,属于基础题.
18.【答案】解:将圆:化成标准方程:,
圆的圆心,半径.
圆心到直线:的距离,
;
当所要求切线的斜率不存在时,过点的直线为,是圆的一条切线;
当所要求切线的斜率存在时,设圆的切线方程为,即,
圆心到直线的距离为,
即,解得:,
此时切线方程为,化简得,
综上所述,所要求的切线方程为:或.
【解析】本题主要考查点线距离公式的应用、圆中的弦长公式的应用及圆的切线方程的求法,属于中档题.
先由题设求得圆的圆心坐标及半径,再求出圆心到直线的距离,最后利用圆中的弦长公式求出弦长即可;
先根据所要求的切线斜率是否存在分类,再利用圆心到所要求切线的距离求出结果即可.
19.【答案】证明:在直三棱柱中,,,,,,两两垂直,以为坐标原点,直线,,分别为轴轴,轴,建立空间直角坐标系,则,,,,.
,,,即,
.
解:假设在上存在点使得平面,则,其中,则,,
又,,平面,所以存在实数,,使成立,
,,,
所以,所以在上存在点使得平面,且为的中点.
【解析】建立空间直角坐标系,用坐标表示点与向量,利用向量的数量积为,证明向量垂直;
假设在上存在点使得平面,则利用平面,存在实数,,使成立,即可求得结论.
本题考查利用向量知识解决立体几何问题,考查线线垂直,考查探索型问题,解题的关键是建立坐标系,用坐标表示向量.
20.【答案】解:不妨设,
因为点到点的距离比它到轴的距离多,
所以,
即,
整理得.
所以点的轨迹方程为;
在点的轨迹中,记:,:,
因为斜率为的直线过定点,
不妨设直线的方程为,
联立,消去并整理得,
当时,,
此时,
可得直线:与轨迹恰好有一个公共点;
当时,
易知.
不妨设直线与轴的交点为,
令,
解得,
若直线与轨迹恰好有一个公共点,
此时,
解得或,
综上,当时,直线与恰有一个公共点.
【解析】由题意,设出点的坐标,列出等式,进而即可求解;
设出直线的方程,将直线的方程与轨迹的方程联立,结合根的判别式进行求解即可.
本题考查轨迹方程以及直线与圆锥曲线的综合问题,考查了逻辑推理、分类讨论和运算能力.
21.【答案】证明:连接,
,分别为直三棱柱的棱和的中点,且,
,,
,,
,
,,
,即,
故以为原点,,,所在直线分别为,,轴建立如图所示的空间直角坐标系,
则,,,,,
设,则,
,,
,即.
解:由知:平面,
平面的一个法向量为,
由知,,,
设平面的法向量为,
则,即,
令,则,,
,
,
,
当时,面与面所成的二面角的余弦值最大为,此时正弦值最小为.
【解析】本题考查空间中线与线的垂直关系,二面角的求法,熟练掌握利用空间向量证明线线垂直和求二面角的方法是解题的关键,考查空间立体感、推理论证能力和运算能力,属于中档题.
连接,易知,,由,再利用勾股定理求得和的长,从而证明,然后以为原点建立空间直角坐标系,证得,即可;
易知平面的一个法向量为,求得平面的法向量,再由空间向量的数量积可得,从而知当时,得解.
22.【答案】解:设椭圆的半焦距为,
由题意可得:,解得,
所以椭圆的方程为.
当直线斜率存在时,设其方程为,,,
联立,可得,
可得,且,
若以为直径的圆过原点,则,
整理得,
代入两式得,整理得,
将式代入式,得恒成立,则,
由题意可设,所以,
因为,
且点到直线:的距离,
可得,
又因为,则点坐标为,
化简可得,
代入椭圆方程可得,整理得,
则,
因为,则,
所以;
当直线斜率不存在时,设,,
则,且,解得,
可知方程为,
因为直线过中点,即为轴,
可知,,,
综上所述:四边形面积的取值范围为.
【解析】根据题意列式求解,,,即可得椭圆方程;
当直线斜率不存在时,可得其方程为,求出;当直线斜率存在时,设其方程为,结合韦达定理、平面向量数量积推出及,再由,计算可得的取值范围,从而得解.
本题主要考查椭圆的标准方程,直线与椭圆的综合,考查运算求解能力,属于难题.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.直线的倾斜角( )
A. B. C. D.
2.圆的圆心坐标为( )
A. B. C. D.
3.设是正三棱锥,是的重心,是上的一点,且,若,则( )
A. B. C. D.
4.万众瞩目的北京冬奥会将于年月日正式开幕,继年北京奥运会之后,国家体育场又名鸟巢将再次承办奥运会开幕式.在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同,扁平程度相同的椭圆,已知大椭圆的长轴长为,短轴长为,小椭圆的短轴长为,则小椭圆的长轴长为.( )
A. B. C. D.
5.已知点,,点在圆上,则的面积的最小值为( )
A. B. C. D.
6.如图,过抛物线的焦点的直线交抛物线于点,,交其准线于点,准线与对称轴交于点,若,且,则为( )
A.
B.
C.
D.
7.设是圆:上的一动点,定点,线段的垂直平分线交线段于点,则点的轨迹方程为( )
A. B. C. D.
8.如图,在正方体中,是中点,点在线段上,若直线与平面所成的角为,则的取值范围是( )
A.
B.
C.
D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.点到直线,的距离可能是( )
A. B. C. D.
10.关于空间向量,以下说法正确的是( )
A. 空间中的三个向量,若有两个向量共线,则这三个向量一定共面
B. 若对空间中任意一点,有,则,,,四点共面
C. 设是空间中的一组基底,则也是空间的一组基底
D. 若,则,是钝角
11.如图所示,正方体的棱长为,线段上有两个动点,且,则下列结论中正确的是( )
A.
B. 平面
C. 三棱锥的体积为定值
D. 异面直线,所成的角为定值
12.已知椭圆:,为的左焦点,直线与交于,两点点在第一象限,直线与椭圆的另一个交点为,则( )
A. B. 当时,的面积为
C. D. 的周长的最大值为
三、填空题:本题共4小题,每小题5分,共20分。
13.若直线:与直线:平行,则直线与之间的距离为______ .
14.已知是不共面向量,,若三个向量共面,则实数 ______ .
15.已知点在圆的外部,则的取值范围是______ .
16.椭圆的光学性质,从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上.已知椭圆:,,为其左、右焦点.是上的动点,点,若的最大值为动直线为此椭圆的切线,右焦点关于直线的对称点,,则:
椭圆的离心率为______;
的取值范围为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
直线经过两直线:和:的交点.
若直线与直线垂直,求直线的方程;
若点到直线的距离为,求直线的方程.
18.本小题分
已知直线和圆.
若直线交圆于,两点,求弦的长;
求过点且与圆相切的直线方程.
19.本小题分
如图所示,在直三棱柱中,,,,.
求证:;
在上是否存在点,使得平面,若存在,确定点位置并说明理由,若不存在,说明理由.
20.本小题分
平面直角坐标系中,点到点的距离比它到轴的距离多,记点的轨迹为.
求轨迹的方程;
设斜率为的直线过定点,若直线与轨迹恰好有一个公共点,求实数的取值范围.
21.本小题分
已知直三棱柱中,侧面为正方形,,,分别为和的中点,为棱上的点..
求证:;
当为何值时,面与面所成的二面角的正弦值最小?
22.本小题分
已知椭圆:的离心率为,点在椭圆上直线与椭圆交于,两点且,其中为坐标原点.
求椭圆的方程;
若过原点的直线与椭圆交于,两点,且过的中点求四边形面积的取值范围.
答案和解析
1.【答案】
【解析】解:由题意可得直线的斜率为,
直线倾斜角为,,则,故.
故选:.
确定直线的斜率,根据斜率与倾斜角的关系,即可求得答案.
本题主要考查直线的倾斜角,属于基础题.
2.【答案】
【解析】解:圆即,
所以圆心坐标为.
故选:.
将圆的方程配成标准式,即可得解.
本题主要考查圆的一般方程,属于基础题.
3.【答案】
【解析】【分析】
本题考查了平面向量基本定理的应用,涉及到三角形重心的性质以及中线的性质,属于基础题.
先取的中点,然后利用三角形法则以及三角形重心的性质和中线的性质即可求解.
【解答】
解:如图所示:
取的中点,连接,
因为是的重心,
所以在上,
因为,
所以
,
所以,
故选:.
4.【答案】
【解析】【分析】
求出大椭圆的离心率等于小椭圆的离心率,然后求解小椭圆的长轴长.
本题考查椭圆的简单性质的应用,是基本知识的考查.
【解答】
解:因为两个椭圆的扁平程度相同,所以椭圆的离心率相同,
所以两个椭圆的离心率相同,
所以,
所以,
所以小椭圆的长轴长为:.
故选:.
5.【答案】
【解析】解:圆的圆心,半径为
,,则,直线:,
圆心到直线的距离,
的面积最小时,点到直线的距离最短,该最短距离即圆心到直线的距离减去圆的半径,
边上高的最小值为,则的最小值为,
故选:.
首先求出直线的方程和线段的长度,利用圆心到直线的距离再减去圆的半径得出的高的最小值,即可求解.
本题主要考查直线和圆的位置关系,属于中档题.
6.【答案】
【解析】解:如图,分别过点、作准线的垂线,垂足分别为点、,
设,则由已知得,由抛物线的定义得,
故,
在直角三角形中,,,
又因为,
则,从而得,
又因为,
所以.
故选:.
分别过点、作准线的垂线,垂足分别为点、,设,根据抛物线的定义以及图象可得,结合已知条件求得,,即可.
本题考查抛物线的几何性质,属中档题.
7.【答案】
【解析】解:线段是线段的垂直平分线交线,
,,
,
,,即点是到定点,距离和为定长的动点,
点的轨迹为椭圆,,,则,
点的轨迹方程为:.
故选:.
利用垂直平分线性质得到,由几何线段的关系得到,根据椭圆的定义即可写出点的轨迹方程.
本题主要考查了轨迹方程的问题,解题的关键是利用了椭圆的定义求得轨迹方程.
8.【答案】
【解析】解:设正方体边长为,.
以为原点,分别以,,为坐标轴建立空间直角坐标系,
则,,,
易证平面,
是平面的一个法向量.
,,
当时取得最大值,当或时,取得最小值.
故选:.
设,以为原点建立坐标系,则是平面的一个法向量.的坐标,得出,关于的函数,根据二次函数的性质得出的取值范围.
本题考查了空间向量与线面角的计算,属于中档题.
9.【答案】
【解析】解:对于直线,,
令,解得,
故直线的必过点为,
设点到直线,的距离为,
则,
所以,,而,
所以,ABC正确,D错误.
故选:.
求出直线的必过点,利用两点间距离公式求出的最大值,进而得到的范围.
本题考查直线的定点以及两点间的距离公式的运用,考查运算求解能力,属于基础题.
10.【答案】
【解析】【分析】
本题考查了空间向量的共线定理,共面定理的应用,考查了基底的概念以及向量的夹角的应用,属于中档题.
根据向量共线的概念即可判断选项A;根据空间向量的基本定理即可判断选项B;根据空间向量的基底的概念即可判断选项C;根据向量夹角的定义即可判断选项D.
【解答】
解:选项A:根据共线向量的概念,可知空间中的三个向量,
若有两个向量共线,则这三个向量一定共面,故A正确;
选项B:因为对空间中任意一点,有,
则,整理可得:,
由平面向量基本定理可知点,,,四点一定共面,故B正确;
选项C:由是空间中的一组基底,则向量不共面,
可得向量也不共面,所以也是空间中的一组基底,故C正确;
选项D:若,则为钝角或,故D错误.
故选:.
11.【答案】
【解析】解:平面,又平面,
,故A正确;
平面,又、在直线上运动,
平面,故B正确;
由于点到直线的距离不变,故的面积为定值.
又点到平面的距离为,故为定值,C正确;
当点在处,为的中点时,异面直线,所成的角是,
当在上底面的中心时,在的位置,异面直线,所成的角是,
显然两个角不相等,不正确.
故选:.
通过直线垂直平面平面,判断是正确的;通过直线平行直线,判断平面,是正确的;计算三角形的面积和到平面的距离是定值,说明是正确的;只需找出两个特殊位置,即可判断是不正确的.
本题考查直线与平面平行的判定,棱锥的体积,异面直线及其所成的角,考查空间想象能力,是中档题.
12.【答案】
【解析】解:椭圆:,所以,,所以,所以A正确;
为的左焦点,直线与交于,两点点在第一象限,直线与椭圆的另一个交点为,
当时,的面积为:,所以不正确;
直线与椭圆的另一个交点为,,的参数方程为:,代入椭圆方程化简可得:,
设,,.
所以C正确;
的周长的最大值为,所以不正确;
故选:.
利用已知条件求解椭圆的离心率,判断;求解三角形的面积判断;利用直线与椭圆的位置关系,转化求解判断,结合椭圆的定义,判断即可.
本题考查直线与椭圆的位置关系的综合应用,椭圆的简单性质的应用,是中档题.
13.【答案】
【解析】解:因为,
所以,解得,
所以直线的方程为,
直线的方程为,即,
所以直线与之间的距离为.
故答案为:.
先求得的值,然后根据两条平行直线间的距离公式求得正确答案.
本题考查平行线距离公式,属于基础题.
14.【答案】
【解析】解:以为空间一组基底,
由于三个向量共面,所以存在,,
使得,
即,
整理得,
所以,解得.
故答案为:.
根据向量共面列方程,化简求得的值.
本题考查向量的共面定理相关知识,属于基础题.
15.【答案】
【解析】解:圆,即,
,即.
点在圆的外部,,.
综上可得,,
故答案为:.
根据圆的标准方程的特征可得,再根据点在圆的外部可得,综合可得实数的取值范围.
本题主要考查圆的标准方程、点和圆的位置关系,属于基础题.
16.【答案】
【解析】解:根据椭圆定义,得,
所以,
因为的最大值为,
因为,所以,即,解得,
所以离心率为;
右焦点关于直线的对称点,
设切点为,由椭圆的光学性质,可得,,三点共线,
所以,
即点的轨迹是以为圆心,半径为的圆,
圆心到直线的距离为,
则圆上的点到直线的距离最小值,最大值,
所以点到直线的距离为,
所以表示点到直线的距离的倍,
则,即.
故答案为:.
根据题意得,所以,求出,即可求出,再求出离心率;根据椭圆的光学性质可得,即点的轨迹是以为圆心,半径为的圆,又表示点到直线的距离的倍,再求出的范围.
本题考查了椭圆的几何性质,与圆有关的最值问题,属于中档题.
17.【答案】解:联立方程组,
解得,
所以交点坐标为,
又因为直线与直线垂直,所以直线的斜率为,
则直线的方程为,即;
当直线的斜率不存在时,直线的方程为,满足点到直线的距离为;
当直线的斜率存在时,设直线的方程为,即,
则点到直线的距离为,
解得,
故直线的方程为,即,
综上可得,直线的方程为或.
【解析】联立方程组,求得两直线的交点坐标,利用垂直关系求得斜率,结合点斜式方程,即可求解;
分直线的斜率存在与不存在,结合点到直线的距离公式求得斜率,利用点斜式方程,即可求解.
本题主要考查了求直线的一般方程,考查了两直线垂直时的斜率关系,以及点到直线的距离公式,属于基础题.
18.【答案】解:将圆:化成标准方程:,
圆的圆心,半径.
圆心到直线:的距离,
;
当所要求切线的斜率不存在时,过点的直线为,是圆的一条切线;
当所要求切线的斜率存在时,设圆的切线方程为,即,
圆心到直线的距离为,
即,解得:,
此时切线方程为,化简得,
综上所述,所要求的切线方程为:或.
【解析】本题主要考查点线距离公式的应用、圆中的弦长公式的应用及圆的切线方程的求法,属于中档题.
先由题设求得圆的圆心坐标及半径,再求出圆心到直线的距离,最后利用圆中的弦长公式求出弦长即可;
先根据所要求的切线斜率是否存在分类,再利用圆心到所要求切线的距离求出结果即可.
19.【答案】证明:在直三棱柱中,,,,,,两两垂直,以为坐标原点,直线,,分别为轴轴,轴,建立空间直角坐标系,则,,,,.
,,,即,
.
解:假设在上存在点使得平面,则,其中,则,,
又,,平面,所以存在实数,,使成立,
,,,
所以,所以在上存在点使得平面,且为的中点.
【解析】建立空间直角坐标系,用坐标表示点与向量,利用向量的数量积为,证明向量垂直;
假设在上存在点使得平面,则利用平面,存在实数,,使成立,即可求得结论.
本题考查利用向量知识解决立体几何问题,考查线线垂直,考查探索型问题,解题的关键是建立坐标系,用坐标表示向量.
20.【答案】解:不妨设,
因为点到点的距离比它到轴的距离多,
所以,
即,
整理得.
所以点的轨迹方程为;
在点的轨迹中,记:,:,
因为斜率为的直线过定点,
不妨设直线的方程为,
联立,消去并整理得,
当时,,
此时,
可得直线:与轨迹恰好有一个公共点;
当时,
易知.
不妨设直线与轴的交点为,
令,
解得,
若直线与轨迹恰好有一个公共点,
此时,
解得或,
综上,当时,直线与恰有一个公共点.
【解析】由题意,设出点的坐标,列出等式,进而即可求解;
设出直线的方程,将直线的方程与轨迹的方程联立,结合根的判别式进行求解即可.
本题考查轨迹方程以及直线与圆锥曲线的综合问题,考查了逻辑推理、分类讨论和运算能力.
21.【答案】证明:连接,
,分别为直三棱柱的棱和的中点,且,
,,
,,
,
,,
,即,
故以为原点,,,所在直线分别为,,轴建立如图所示的空间直角坐标系,
则,,,,,
设,则,
,,
,即.
解:由知:平面,
平面的一个法向量为,
由知,,,
设平面的法向量为,
则,即,
令,则,,
,
,
,
当时,面与面所成的二面角的余弦值最大为,此时正弦值最小为.
【解析】本题考查空间中线与线的垂直关系,二面角的求法,熟练掌握利用空间向量证明线线垂直和求二面角的方法是解题的关键,考查空间立体感、推理论证能力和运算能力,属于中档题.
连接,易知,,由,再利用勾股定理求得和的长,从而证明,然后以为原点建立空间直角坐标系,证得,即可;
易知平面的一个法向量为,求得平面的法向量,再由空间向量的数量积可得,从而知当时,得解.
22.【答案】解:设椭圆的半焦距为,
由题意可得:,解得,
所以椭圆的方程为.
当直线斜率存在时,设其方程为,,,
联立,可得,
可得,且,
若以为直径的圆过原点,则,
整理得,
代入两式得,整理得,
将式代入式,得恒成立,则,
由题意可设,所以,
因为,
且点到直线:的距离,
可得,
又因为,则点坐标为,
化简可得,
代入椭圆方程可得,整理得,
则,
因为,则,
所以;
当直线斜率不存在时,设,,
则,且,解得,
可知方程为,
因为直线过中点,即为轴,
可知,,,
综上所述:四边形面积的取值范围为.
【解析】根据题意列式求解,,,即可得椭圆方程;
当直线斜率不存在时,可得其方程为,求出;当直线斜率存在时,设其方程为,结合韦达定理、平面向量数量积推出及,再由,计算可得的取值范围,从而得解.
本题主要考查椭圆的标准方程,直线与椭圆的综合,考查运算求解能力,属于难题.
第1页,共1页
同课章节目录
