人教版六年级上册数学《圆的面积》 课件(共25张PPT)
文档属性
| 名称 | 人教版六年级上册数学《圆的面积》 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 08:00:50 | ||
图片预览







文档简介
(共25张PPT)
《圆的面积》
人教版数学六年级上册第五单元
(一)创设情境,提出问题
用31.4米长的篱笆重新围一块地,既能让更多的小朋友同时观看小鸭子,也让小鸭子有更多的活动空间,你们有什么好想法?
周长一定时,围成正方形面积最大,最好围正方形。
我们新学了圆,围成圆面积会不会更大呢?
(二)理解问题,制定计划
提问:你怎么理解这个问题?
三年级时已经研究过周长相等时正方形的面积最大,只需要比较周长相等时正方形和圆的面积谁大就可以了。
追问:你打算怎么解决这个问题?
首先,计算周长是31.4米的正方形的面积,其次计算周长是31.4米的圆的面积,最后比较大小,得出结论
(三)动手操作,研究圆的面积
1. 确定范围,初步猜想
圆面积的计算公式还没有研究?
以前学面图形的面积计算公式都是由线段围成的图形,而圆是由曲线围成的图形,该怎样把圆转化成以前学习的图形得到圆面积的计算公式呢?
提问:那么在解决这个问题的过程中你们遇到了什么困难?
(三)动手操作,研究圆的面积
1. 确定范围,初步猜想
我知道了它一定比2r2大比4r2小,我们认识了圆周率π,有可能是r2的π倍,也就是πr2。
监控:那这节课我们就一起来研究圆的面积,在研究之前你能猜猜圆的面积公式是什么吗?
提问:我们该怎样得到圆的面积呢?你们有什么方法或经验吗?
在学习长正方形的面积时,是用面积单位测量的,所以我觉得圆的面积也可以用面积单位去测量。
我们知道正多边形的边数越多越接近圆。那么圆的面积我认为也可以借助这种方法来研究。
在学习平行四边形、三角形、梯形的面积时,就是把它们转化成了原来学习过的图形,所以我想把圆也可以转化成学过的图形。
(三)动手操作,研究圆的面积
2.选择方法,自主探究
活动要求:
1.选择你喜欢的方法自主探究圆的面积的计算方法,将你的想法记录在学习单上。
2.先独立思考,再小组内交流:你是怎么想的?
3.时间:6分钟。
(三)动手操作,研究圆的面积
方法一:数方格
(1)估数法
在圆上画出方格,每个方格是1平方厘米,大于半个格的按照1平方厘米计算,小于半个格按照0平方厘米计算。这样就可以数出圆的面积了。
监控:看完他的这种方法,你们有什么想说的吗?
3.交流研讨资源,引发学生深入思考
(三)动手操作,研究圆的面积
方法一:数方格
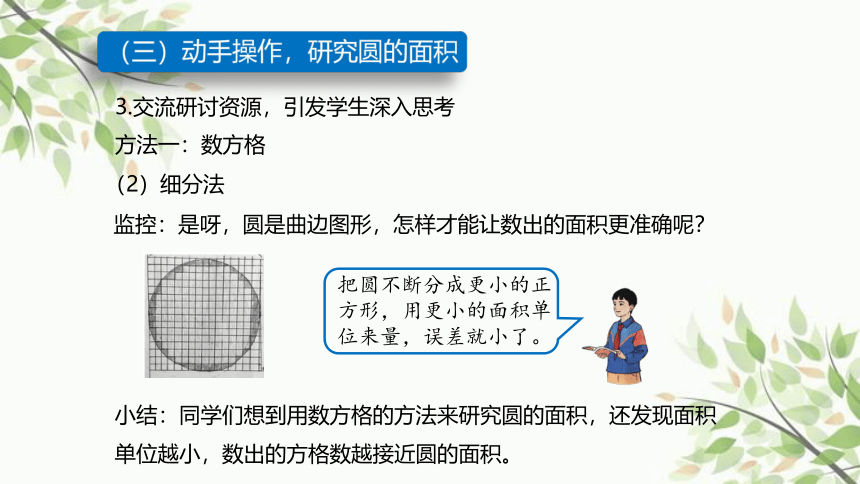
(2)细分法
把圆不断分成更小的正方形,用更小的面积单位来量,误差就小了。
监控:是呀,圆是曲边图形,怎样才能让数出的面积更准确呢?
小结:同学们想到用数方格的方法来研究圆的面积,还发现面积单位越小,数出的方格数越接近圆的面积。
3.交流研讨资源,引发学生深入思考
(三)动手操作,研究圆的面积
方法二:增加内接正多边形的边数
(1)感悟极限
提问1:你怎么想到在圆内画正方形呢?
提问2: 针对他的研究方法,你有什么想说的?
这样只能得到圆面积的范围,无法准确得到圆的面积,有误差怎么办?
在原有图形的基础上增加三角形,并画出了正八边形,这样就与圆的面积更接近了。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法二:增加正多边形的边数
(1)感悟极限
追问:如何让测量出的面积更接近于圆呢?
预设:在正八边形的基础上,再加小三角形,画出正十六边形、正三十二边形。
边数=4
边数=8
边数=16
边数=32
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法二:增加正多边形的边数
(1)感悟极限
提问1:观察正多边形的面积不断逼近圆的面积,说说你有什么发现?
提问2:接下来我们怎么得到圆的面积?
(2)介绍割圆术
直
曲
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(1)初步探究
展示作品1:
追问2:4个小扇形的边的弯曲度太大了,那怎样才能让这些边
的弯曲度变小呢?
追问1:为什么不是平行四边形?
把圆平均分成4份,拼在一起后的图形有点像平行四边形。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(2)深度思考
展示作品2:
预设1:把圆平均分成4份、8份、16份后,都可以拼成一个近似的平行四边形。
提问:对比观察这三个作品,你有什么发现呢?
展示作品3:
预设2:分的份数越多,拼成的图形越行四边形。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(3)获得确定结果
提问:刚才同学们说到了问题的关键,现在继续想一想,如果把圆平均分成 32份,再拼到一起会怎样呢?
监控:如果现在平均分成64份又会是什么样子呢?请大家先想一想。
课件出示:
预设:拼成的图形更行四边形了。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(3)获得确定结果
课件出示:
师:继续分,平均分成128份,现在像什么图形?
课件出示:
追问:如果继续分,分得的份数更多呢?甚至无限多的等份,想象以下拼出的图形会是——
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
活动要求:
(1)转化:在纸的右边,尝试把16等分圆转化成我们学过的平面图形,并贴好。
(2)联系:观察转化后图形的各部分与圆有什么联系,在图上标出来。
(3)推导:在纸的左边记录你们小组推导圆面积计算方法的过程。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
谈话:解决了化曲为直的问题,借助这些近似的小三角形,我们继续研究圆面积的计算方法。
(1)拼成平行四边形(长方形)
把圆拼成平行四边形后,平行四边形的面积等于圆的面积,平行四边形的底相当于圆周长的一半,周长=2πr,一半就是πr,平行四边形的高相当于圆的半径。根据平行四边形面积=底×高,得到圆的面积是πr×r=πr 。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
(2)拼成三角形
把圆平均分成 16 份后拼成了近似的三角形,三角形的面积等于圆的面积1 个小三角形的底近似于圆周长的 1/16,4 份就是圆周长的 4/16 也就是 1/4。高是 4r。根据三角形面积=底×高÷2,就能得到圆的面积公式是πr 。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
(3)拼成梯形
把圆平均分成了 16 份,拼成了近似的梯形,梯形的面积等于圆的面积。一个近似的小三角形的边长近似于 1/16c,梯形上底有 3 个小三角形的边长,近似于 3/16c,下底有 5 个小三角形的边长就近似于 5/16c,有 2 层,高近似于 2r。梯形面积公式等于(上底+下底)×高÷2,可以推出圆的面积公式是πr 。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
(4)分成多个三角形
把圆平均分成多个三角形,三角形的面积和等于圆的面积。利用等底等高把这些三角形合成一个大三角形,它的底是圆的周长,高是圆的半径,除以2就可以算出面积,即2πr×r÷2,也就是πr×r=πr2。
提问:还有同学也是将圆无限细分,并与我们已学图形建立了联系,看看你能读懂他的想法吗?
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
5.回忆学习过程,积累学习经验
提问1:回忆学习圆面积的过程,仔细观察一下,在图形的转化过程中什么变了,什么没变?
提问2:同学们再回头看,开始有同学说圆的面积的大致范围在2r2和4r2之间,这个结论对吗?
半周半径相乘,得积步。
(三)动手操作,研究圆的面积
1.用31.4米长的篱笆重新围一块地,既能让更多的小朋友同时观看小鸭子,也让小鸭子有更多的活动空间,你们有什么好想法?
(四)执行计划,解决问题
2.如图,已知圆内阴影部分的面积是7cm2, 那么一个圆的面积多少呢?
(四)执行计划,解决问题
提问:回顾本节课,我们是怎样研究圆的面积的?你还有什么想研究的问题?
预设1:我们把圆转化成学过的图形,然后找到了转化后的图形与圆之间的关系,借助已知图形的面积公式推导出了圆的面积公式。
预设2:我们通过化曲为直,可以将圆这个曲边图形转化成之前学过的直边的图形,我想研究圆柱的体积是否可以转化为长方体,从而推导出体积公式。
板书设计:
(五)回顾反思,课堂总结
《圆的面积》
人教版数学六年级上册第五单元
(一)创设情境,提出问题
用31.4米长的篱笆重新围一块地,既能让更多的小朋友同时观看小鸭子,也让小鸭子有更多的活动空间,你们有什么好想法?
周长一定时,围成正方形面积最大,最好围正方形。
我们新学了圆,围成圆面积会不会更大呢?
(二)理解问题,制定计划
提问:你怎么理解这个问题?
三年级时已经研究过周长相等时正方形的面积最大,只需要比较周长相等时正方形和圆的面积谁大就可以了。
追问:你打算怎么解决这个问题?
首先,计算周长是31.4米的正方形的面积,其次计算周长是31.4米的圆的面积,最后比较大小,得出结论
(三)动手操作,研究圆的面积
1. 确定范围,初步猜想
圆面积的计算公式还没有研究?
以前学面图形的面积计算公式都是由线段围成的图形,而圆是由曲线围成的图形,该怎样把圆转化成以前学习的图形得到圆面积的计算公式呢?
提问:那么在解决这个问题的过程中你们遇到了什么困难?
(三)动手操作,研究圆的面积
1. 确定范围,初步猜想
我知道了它一定比2r2大比4r2小,我们认识了圆周率π,有可能是r2的π倍,也就是πr2。
监控:那这节课我们就一起来研究圆的面积,在研究之前你能猜猜圆的面积公式是什么吗?
提问:我们该怎样得到圆的面积呢?你们有什么方法或经验吗?
在学习长正方形的面积时,是用面积单位测量的,所以我觉得圆的面积也可以用面积单位去测量。
我们知道正多边形的边数越多越接近圆。那么圆的面积我认为也可以借助这种方法来研究。
在学习平行四边形、三角形、梯形的面积时,就是把它们转化成了原来学习过的图形,所以我想把圆也可以转化成学过的图形。
(三)动手操作,研究圆的面积
2.选择方法,自主探究
活动要求:
1.选择你喜欢的方法自主探究圆的面积的计算方法,将你的想法记录在学习单上。
2.先独立思考,再小组内交流:你是怎么想的?
3.时间:6分钟。
(三)动手操作,研究圆的面积
方法一:数方格
(1)估数法
在圆上画出方格,每个方格是1平方厘米,大于半个格的按照1平方厘米计算,小于半个格按照0平方厘米计算。这样就可以数出圆的面积了。
监控:看完他的这种方法,你们有什么想说的吗?
3.交流研讨资源,引发学生深入思考
(三)动手操作,研究圆的面积
方法一:数方格
(2)细分法
把圆不断分成更小的正方形,用更小的面积单位来量,误差就小了。
监控:是呀,圆是曲边图形,怎样才能让数出的面积更准确呢?
小结:同学们想到用数方格的方法来研究圆的面积,还发现面积单位越小,数出的方格数越接近圆的面积。
3.交流研讨资源,引发学生深入思考
(三)动手操作,研究圆的面积
方法二:增加内接正多边形的边数
(1)感悟极限
提问1:你怎么想到在圆内画正方形呢?
提问2: 针对他的研究方法,你有什么想说的?
这样只能得到圆面积的范围,无法准确得到圆的面积,有误差怎么办?
在原有图形的基础上增加三角形,并画出了正八边形,这样就与圆的面积更接近了。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法二:增加正多边形的边数
(1)感悟极限
追问:如何让测量出的面积更接近于圆呢?
预设:在正八边形的基础上,再加小三角形,画出正十六边形、正三十二边形。
边数=4
边数=8
边数=16
边数=32
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法二:增加正多边形的边数
(1)感悟极限
提问1:观察正多边形的面积不断逼近圆的面积,说说你有什么发现?
提问2:接下来我们怎么得到圆的面积?
(2)介绍割圆术
直
曲
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(1)初步探究
展示作品1:
追问2:4个小扇形的边的弯曲度太大了,那怎样才能让这些边
的弯曲度变小呢?
追问1:为什么不是平行四边形?
把圆平均分成4份,拼在一起后的图形有点像平行四边形。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(2)深度思考
展示作品2:
预设1:把圆平均分成4份、8份、16份后,都可以拼成一个近似的平行四边形。
提问:对比观察这三个作品,你有什么发现呢?
展示作品3:
预设2:分的份数越多,拼成的图形越行四边形。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(3)获得确定结果
提问:刚才同学们说到了问题的关键,现在继续想一想,如果把圆平均分成 32份,再拼到一起会怎样呢?
监控:如果现在平均分成64份又会是什么样子呢?请大家先想一想。
课件出示:
预设:拼成的图形更行四边形了。
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
方法三:转化
(3)获得确定结果
课件出示:
师:继续分,平均分成128份,现在像什么图形?
课件出示:
追问:如果继续分,分得的份数更多呢?甚至无限多的等份,想象以下拼出的图形会是——
(三)动手操作,研究圆的面积
3.交流研讨资源,引发学生深入思考
活动要求:
(1)转化:在纸的右边,尝试把16等分圆转化成我们学过的平面图形,并贴好。
(2)联系:观察转化后图形的各部分与圆有什么联系,在图上标出来。
(3)推导:在纸的左边记录你们小组推导圆面积计算方法的过程。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
谈话:解决了化曲为直的问题,借助这些近似的小三角形,我们继续研究圆面积的计算方法。
(1)拼成平行四边形(长方形)
把圆拼成平行四边形后,平行四边形的面积等于圆的面积,平行四边形的底相当于圆周长的一半,周长=2πr,一半就是πr,平行四边形的高相当于圆的半径。根据平行四边形面积=底×高,得到圆的面积是πr×r=πr 。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
(2)拼成三角形
把圆平均分成 16 份后拼成了近似的三角形,三角形的面积等于圆的面积1 个小三角形的底近似于圆周长的 1/16,4 份就是圆周长的 4/16 也就是 1/4。高是 4r。根据三角形面积=底×高÷2,就能得到圆的面积公式是πr 。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
(3)拼成梯形
把圆平均分成了 16 份,拼成了近似的梯形,梯形的面积等于圆的面积。一个近似的小三角形的边长近似于 1/16c,梯形上底有 3 个小三角形的边长,近似于 3/16c,下底有 5 个小三角形的边长就近似于 5/16c,有 2 层,高近似于 2r。梯形面积公式等于(上底+下底)×高÷2,可以推出圆的面积公式是πr 。
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
(4)分成多个三角形
把圆平均分成多个三角形,三角形的面积和等于圆的面积。利用等底等高把这些三角形合成一个大三角形,它的底是圆的周长,高是圆的半径,除以2就可以算出面积,即2πr×r÷2,也就是πr×r=πr2。
提问:还有同学也是将圆无限细分,并与我们已学图形建立了联系,看看你能读懂他的想法吗?
(三)动手操作,研究圆的面积
4.探索问题解决策略,积累数学学习经验
5.回忆学习过程,积累学习经验
提问1:回忆学习圆面积的过程,仔细观察一下,在图形的转化过程中什么变了,什么没变?
提问2:同学们再回头看,开始有同学说圆的面积的大致范围在2r2和4r2之间,这个结论对吗?
半周半径相乘,得积步。
(三)动手操作,研究圆的面积
1.用31.4米长的篱笆重新围一块地,既能让更多的小朋友同时观看小鸭子,也让小鸭子有更多的活动空间,你们有什么好想法?
(四)执行计划,解决问题
2.如图,已知圆内阴影部分的面积是7cm2, 那么一个圆的面积多少呢?
(四)执行计划,解决问题
提问:回顾本节课,我们是怎样研究圆的面积的?你还有什么想研究的问题?
预设1:我们把圆转化成学过的图形,然后找到了转化后的图形与圆之间的关系,借助已知图形的面积公式推导出了圆的面积公式。
预设2:我们通过化曲为直,可以将圆这个曲边图形转化成之前学过的直边的图形,我想研究圆柱的体积是否可以转化为长方体,从而推导出体积公式。
板书设计:
(五)回顾反思,课堂总结
