2.5 二次函数与一元二次方程 第2课时 课件(共13张PPT) 2023-2024学年初中数学北师版九年级下册
文档属性
| 名称 | 2.5 二次函数与一元二次方程 第2课时 课件(共13张PPT) 2023-2024学年初中数学北师版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 727.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:31:24 | ||
图片预览




文档简介
(共13张PPT)
第二章 二次函数
2.5 二次函数与一元二次方程
第2课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.会用二次函数图象求一元二次方程的近似解; (重点)
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:上节课我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0)之间的关系,那么如何利用二次函数图象直接求出一元二次方程的根呢
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:利用图象法求一元二次方程的近似根
试一试1:求一元二次方程x2-2x-1=0的根的近似值(精确到0.1).
问题探究:
根据上节课的内容,一元二次方程有何联系?
一元二次方程的根就是二次函数的图象与x轴的交点横坐标
合作探究
当堂检测
学习目标
课堂总结
自主学习
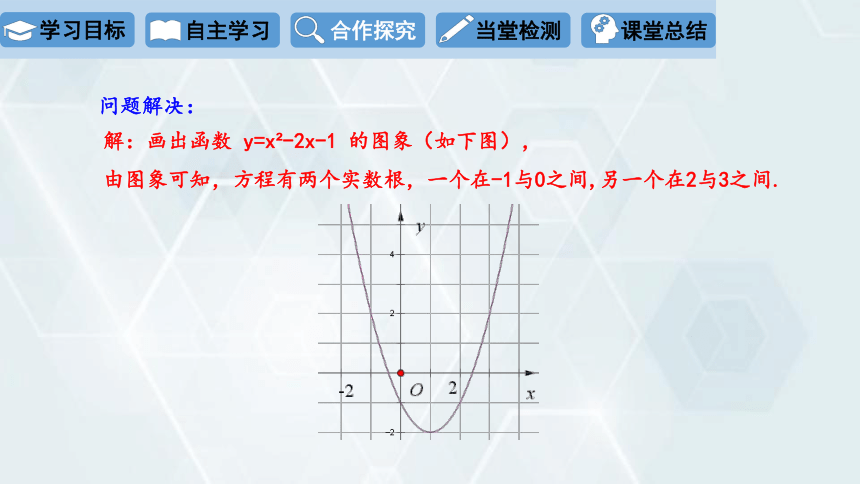
问题解决:
解:画出函数 y=x -2x-1 的图象(如下图),
由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
合作探究
当堂检测
学习目标
课堂总结
自主学习
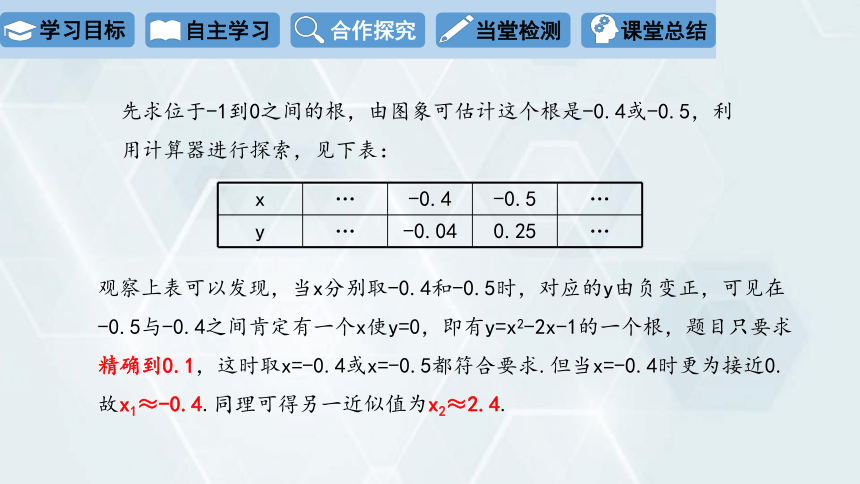
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x … -0.4 -0.5 …
y … -0.04 0.25 …
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法小结:
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 y=ax2+bx+c的图象与x轴的交点的横坐标;
(3)确定方程ax2+bx+c=0的解.(借助计算器)
利用二次函数的图象求一元二次方程的ax2+bx+c=0的近似根:
合作探究
当堂检测
学习目标
课堂总结
自主学习
试一试2:你还能利用y=x -2x-1的图象求一元二次方程x -2x-1=3的近似根吗(精确到0.1)?
解:在y=x -2x-1的图象中作直线y=3,
再用图象法求出直线与抛物线交点的横坐标,则横坐标的近似值即为所求方程的近似根.
y=3
因此,x=3.2和x=-1.2是方程的两个近似根.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
一元二次方程ax2+bx+c=m的根就是二次函数y=ax2+bx+c 与直线y=m(m是实数)图象交点的横坐标 .
既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.小颖用几何画板软件探索方程ax2+bx+c=0的实数根,作出了如图所示的图象,观察得一个近似根为x1=-4.5,则方程的另一个近似根为x2=________(精确到0.1).
2.5
合作探究
当堂检测
学习目标
课堂总结
自主学习
C
2.根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A.8<x<9 B.9<x<10 C.10<x<11 D.11<x<12
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.利用二次函数的图象求一元二次方程x +x-1=0的近似解.
1
2
0
-1
-2
x
1
2
3
4
5
6
y
y=x +x-1
解:设y=x2+x-1,则方程x2+x-1=0的解就是该函数图象与x轴交点的横坐标.
在直角坐标系中画出函数y=x2+x-1的图象,得到与x轴的交点为A,B,则点A,B的横坐标x1,x2就是方程的解.
观察图象,得到点A的横坐标x1≈0.6,点B的横坐标x2≈-1.6.所以方程x2+x-1=0的近似解为x1≈0.6,x2≈-1.6
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
二次函数图象
由图象与x轴的交点位置,
判断方程根的近似值
一元二次方程的根
一元二次不等式的解集
第二章 二次函数
2.5 二次函数与一元二次方程
第2课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.会用二次函数图象求一元二次方程的近似解; (重点)
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:上节课我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0)之间的关系,那么如何利用二次函数图象直接求出一元二次方程的根呢
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:利用图象法求一元二次方程的近似根
试一试1:求一元二次方程x2-2x-1=0的根的近似值(精确到0.1).
问题探究:
根据上节课的内容,一元二次方程有何联系?
一元二次方程的根就是二次函数的图象与x轴的交点横坐标
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
解:画出函数 y=x -2x-1 的图象(如下图),
由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
合作探究
当堂检测
学习目标
课堂总结
自主学习
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x … -0.4 -0.5 …
y … -0.04 0.25 …
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法小结:
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 y=ax2+bx+c的图象与x轴的交点的横坐标;
(3)确定方程ax2+bx+c=0的解.(借助计算器)
利用二次函数的图象求一元二次方程的ax2+bx+c=0的近似根:
合作探究
当堂检测
学习目标
课堂总结
自主学习
试一试2:你还能利用y=x -2x-1的图象求一元二次方程x -2x-1=3的近似根吗(精确到0.1)?
解:在y=x -2x-1的图象中作直线y=3,
再用图象法求出直线与抛物线交点的横坐标,则横坐标的近似值即为所求方程的近似根.
y=3
因此,x=3.2和x=-1.2是方程的两个近似根.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
一元二次方程ax2+bx+c=m的根就是二次函数y=ax2+bx+c 与直线y=m(m是实数)图象交点的横坐标 .
既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.小颖用几何画板软件探索方程ax2+bx+c=0的实数根,作出了如图所示的图象,观察得一个近似根为x1=-4.5,则方程的另一个近似根为x2=________(精确到0.1).
2.5
合作探究
当堂检测
学习目标
课堂总结
自主学习
C
2.根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A.8<x<9 B.9<x<10 C.10<x<11 D.11<x<12
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.利用二次函数的图象求一元二次方程x +x-1=0的近似解.
1
2
0
-1
-2
x
1
2
3
4
5
6
y
y=x +x-1
解:设y=x2+x-1,则方程x2+x-1=0的解就是该函数图象与x轴交点的横坐标.
在直角坐标系中画出函数y=x2+x-1的图象,得到与x轴的交点为A,B,则点A,B的横坐标x1,x2就是方程的解.
观察图象,得到点A的横坐标x1≈0.6,点B的横坐标x2≈-1.6.所以方程x2+x-1=0的近似解为x1≈0.6,x2≈-1.6
A
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
二次函数图象
由图象与x轴的交点位置,
判断方程根的近似值
一元二次方程的根
一元二次不等式的解集
