3.1 圆 课件(共20张PPT) 2023-2024学年初中数学北师版九年级下册
文档属性
| 名称 | 3.1 圆 课件(共20张PPT) 2023-2024学年初中数学北师版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
第三章 圆
3.1 圆
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.知道圆的形成过程及其相关概念
2.知道点与圆的位置关系,会利用点到圆心的距离和圆的半径之间的数量关系判定点和圆的位置关系(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
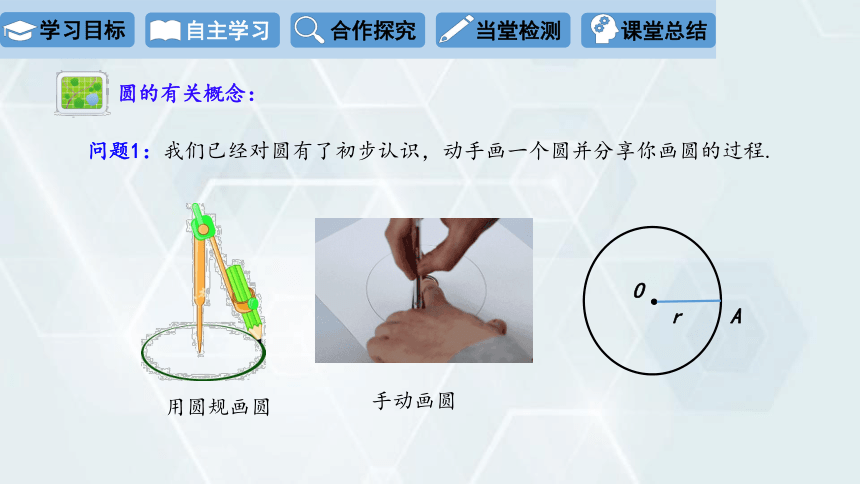
问题1:我们已经对圆有了初步认识,动手画一个圆并分享你画圆的过程.
用圆规画圆
A
O
r
手动画圆
圆的有关概念:
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
O
r
圆的定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
概念:固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
O
r
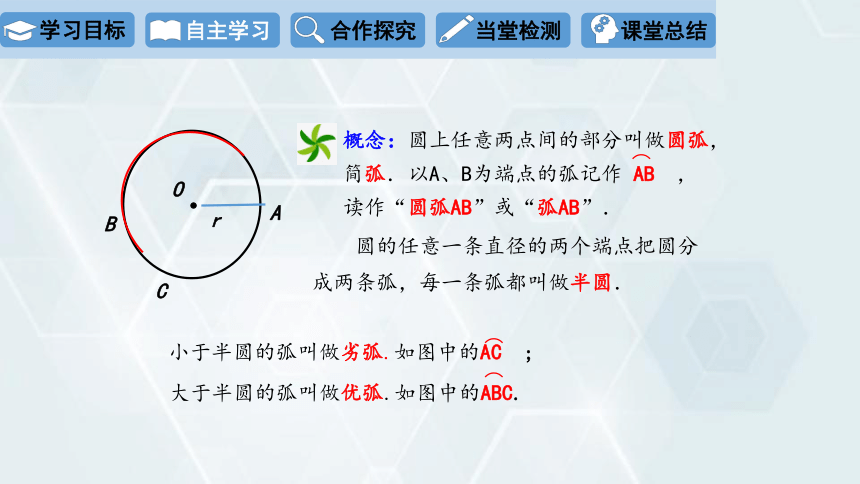
概念:圆上任意两点间的部分叫做圆弧,简弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
C
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
r
O'
r'
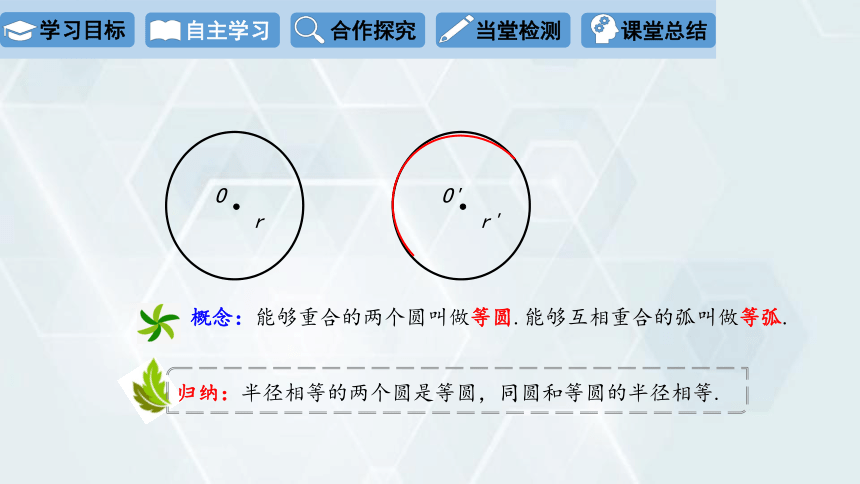
概念:能够重合的两个圆叫做等圆.能够互相重合的弧叫做等弧.
归纳:半径相等的两个圆是等圆,同圆和等圆的半径相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
判断下列说法的正误.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
试一试:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:用图形表示点与圆的位置关系
问题1:足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?
合作探究
当堂检测
学习目标
课堂总结
自主学习
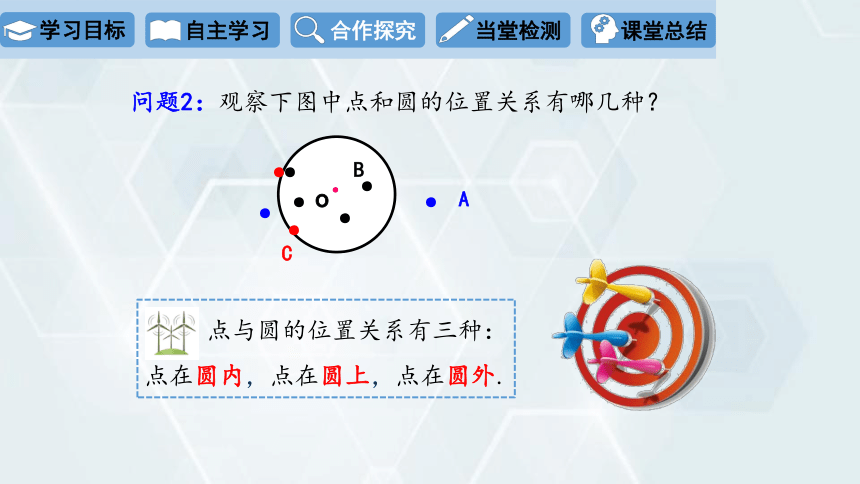
问题2:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
. B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. M, N及点A,B,C,D的位置如图所示,下列说法:
(1)点A既在 M外也在 N外;(2)点B既在 M上也在 N上;
(3)点C既在 M内也在 N内;(4)点D既在 M内也在 N内.
其中,说法正确的有 ( )
A.1个 B.2个 C.3个 D.4个
D
N
M
C
B
C
练一练:
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:用数量表示点与圆的位置关系
问题:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
p
d
p
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
符号“ ”读作“等
价于”,它表示从左端
可以推出右端,从右端
也可以推出左端.
合作探究
当堂检测
学习目标
课堂总结
自主学习
试一试:
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
o
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:已知⊙A的半径r=3 cm.
(1) 因为 ,所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r,所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.
练一练:
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,圆中以A为一个端点的优弧有 条,劣弧有 条.
直径
半径
一
二
四
四
A
B
C
D
O
F
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为__________.
(-1,-2)
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.(1)以点C为圆心,6为半径作圆C,试判断点A,D,B与⊙C的位置关系;
解:在△ABC中,
由勾股定理得AC=6,
由三角形面积公式得
∴CD=4.8.
(1)∵AC=6,∴点A在⊙C上.
∵BC=8>6,∴点B在⊙C外.
∵CD=4.8<6,
∴点D在⊙C内.
S△ABC= AC·BC= AB·CD,
∠ACB=90°,AB=10,BC=8,CD⊥AB,
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.(2)⊙C的半径为多少时,点O在⊙C上?
∴⊙C的半径为5时,点O在⊙C上.
解:(2)∵点O为AB的中点,
∠ACB=90°,
∴OC= AB=5,
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆
定义
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
等圆
同圆
等弧
能够互相重合的两段弧
1.圆的有关概念
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.点与圆的位置关系
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
第三章 圆
3.1 圆
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.知道圆的形成过程及其相关概念
2.知道点与圆的位置关系,会利用点到圆心的距离和圆的半径之间的数量关系判定点和圆的位置关系(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题1:我们已经对圆有了初步认识,动手画一个圆并分享你画圆的过程.
用圆规画圆
A
O
r
手动画圆
圆的有关概念:
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
O
r
圆的定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
概念:固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
O
r
概念:圆上任意两点间的部分叫做圆弧,简弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
C
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
r
O'
r'
概念:能够重合的两个圆叫做等圆.能够互相重合的弧叫做等弧.
归纳:半径相等的两个圆是等圆,同圆和等圆的半径相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
判断下列说法的正误.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
试一试:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:用图形表示点与圆的位置关系
问题1:足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
. B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. M, N及点A,B,C,D的位置如图所示,下列说法:
(1)点A既在 M外也在 N外;(2)点B既在 M上也在 N上;
(3)点C既在 M内也在 N内;(4)点D既在 M内也在 N内.
其中,说法正确的有 ( )
A.1个 B.2个 C.3个 D.4个
D
N
M
C
B
C
练一练:
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:用数量表示点与圆的位置关系
问题:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
p
d
p
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
符号“ ”读作“等
价于”,它表示从左端
可以推出右端,从右端
也可以推出左端.
合作探究
当堂检测
学习目标
课堂总结
自主学习
试一试:
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
o
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:已知⊙A的半径r=3 cm.
(1) 因为 ,所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r,所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.
练一练:
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,圆中以A为一个端点的优弧有 条,劣弧有 条.
直径
半径
一
二
四
四
A
B
C
D
O
F
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为__________.
(-1,-2)
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.(1)以点C为圆心,6为半径作圆C,试判断点A,D,B与⊙C的位置关系;
解:在△ABC中,
由勾股定理得AC=6,
由三角形面积公式得
∴CD=4.8.
(1)∵AC=6,∴点A在⊙C上.
∵BC=8>6,∴点B在⊙C外.
∵CD=4.8<6,
∴点D在⊙C内.
S△ABC= AC·BC= AB·CD,
∠ACB=90°,AB=10,BC=8,CD⊥AB,
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.(2)⊙C的半径为多少时,点O在⊙C上?
∴⊙C的半径为5时,点O在⊙C上.
解:(2)∵点O为AB的中点,
∠ACB=90°,
∴OC= AB=5,
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆
定义
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
等圆
同圆
等弧
能够互相重合的两段弧
1.圆的有关概念
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.点与圆的位置关系
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
