3.5 确定圆的条件 课件 (共18张PPT)2023-2024学年初中数学北师版九年级下册
文档属性
| 名称 | 3.5 确定圆的条件 课件 (共18张PPT)2023-2024学年初中数学北师版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第三章 圆
3.5 确定圆的条件
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解并掌握三点确定圆的条件并会应用. (重点)
2.理解并掌握三角形的外接圆及外心的概念.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.过一点可以作几条直线?
2.过几点确定一条直线?
复习回顾:
无数条
两点确定一条直线
思考:几点可以确定一个圆?
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:探索确定圆的条件
问题提出:经过一点可以作几个圆 经过两点,三点,…,呢?
A
●A
●B
●O
●O
●O
合作探究
当堂检测
学习目标
课堂总结
自主学习
●A
●B
●O
●O
●O
●O
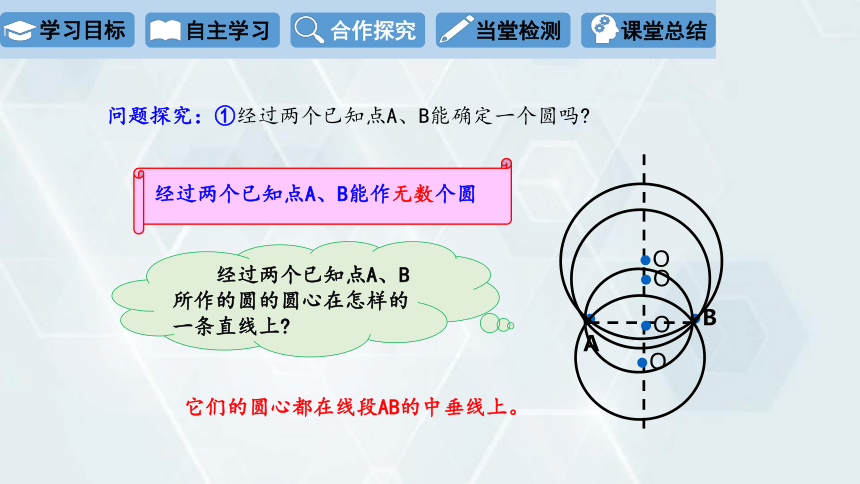
问题探究:①经过两个已知点A、B能确定一个圆吗
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的中垂线上。
合作探究
当堂检测
学习目标
课堂总结
自主学习
经过A、B、C 三个点能不能作圆?如果能,可以作多少个?圆心在什么位置?如果不能,请说明理由.
合作探究
当堂检测
学习目标
课堂总结
自主学习
②以O为圆心,OA(或OB,或OC)为半径,作⊙O即可.请你证明你做得圆符合要求.
证明:∵点O在AB的垂直平分线上,
∴⊙O就是所求作的圆,
∴OA=OB.
同理,OB=OC.
∴OA=OB=OC.
∴点A,B,C在以O为圆心的圆上.
┓
E
D
┏
G
F
●A
●B
●C
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
③从上述作图中可以看出A、B、C三点不在一条直线上,那么在同一直线的三点能作圆吗?为什么?
A
B
C
根据作圆的方法,分别作两点连线的垂直平分线,交于一点,而三点共线的情况,任意两条垂直平分线都不可能相交,所以在同一条直线的三点不能作圆。
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
三点定圆
定理:不在一条直线上的三个点确定一个圆.
∵直线ED和FG只有一个交点O,并且点O到A,B,C三个点的距离相等,
∴经过点A,B,C三点可以作一个圆,并且只能作一个圆.
●C
●A
┓
E
D
┏
G
F
●B
●C
●A
●O
┓
D
┏
G
F
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
A.E、F、G B.F、G、H C.G、H、E D.H、E、F
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:三角形的外接圆及外心
问题提出:已知△ABC,用直尺和圆规作出过点A,B,C的圆.
A
B
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
N
M
F
E
A
B
C
作法:
1.作线段AB的垂直平分线MN;
2.作线段AC的垂直平分线EF,交MN于点O;
3.连接OB.
4.以O为圆心,OB为半径作圆.
⊙O就是所求作的圆.
合作探究
当堂检测
学习目标
课堂总结
自主学习
揭示概念:
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
三角形的外接圆
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况
锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
小结:
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.下列命题不正确的是( )
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,A,B是已知圆上两点,用直尺和圆规作以AB为底边的圆内接等腰三角形.这样的三角形能作几个?
解:能作2个.作AB的垂直平分线与圆有两个交点,则得到相应的两个等腰三角形,如图:
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
确定圆的条件
1.确定圆的条件:不在同一条直线的三点共圆
2.三角形的外接圆:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
第三章 圆
3.5 确定圆的条件
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解并掌握三点确定圆的条件并会应用. (重点)
2.理解并掌握三角形的外接圆及外心的概念.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.过一点可以作几条直线?
2.过几点确定一条直线?
复习回顾:
无数条
两点确定一条直线
思考:几点可以确定一个圆?
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:探索确定圆的条件
问题提出:经过一点可以作几个圆 经过两点,三点,…,呢?
A
●A
●B
●O
●O
●O
合作探究
当堂检测
学习目标
课堂总结
自主学习
●A
●B
●O
●O
●O
●O
问题探究:①经过两个已知点A、B能确定一个圆吗
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的中垂线上。
合作探究
当堂检测
学习目标
课堂总结
自主学习
经过A、B、C 三个点能不能作圆?如果能,可以作多少个?圆心在什么位置?如果不能,请说明理由.
合作探究
当堂检测
学习目标
课堂总结
自主学习
②以O为圆心,OA(或OB,或OC)为半径,作⊙O即可.请你证明你做得圆符合要求.
证明:∵点O在AB的垂直平分线上,
∴⊙O就是所求作的圆,
∴OA=OB.
同理,OB=OC.
∴OA=OB=OC.
∴点A,B,C在以O为圆心的圆上.
┓
E
D
┏
G
F
●A
●B
●C
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
③从上述作图中可以看出A、B、C三点不在一条直线上,那么在同一直线的三点能作圆吗?为什么?
A
B
C
根据作圆的方法,分别作两点连线的垂直平分线,交于一点,而三点共线的情况,任意两条垂直平分线都不可能相交,所以在同一条直线的三点不能作圆。
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
三点定圆
定理:不在一条直线上的三个点确定一个圆.
∵直线ED和FG只有一个交点O,并且点O到A,B,C三个点的距离相等,
∴经过点A,B,C三点可以作一个圆,并且只能作一个圆.
●C
●A
┓
E
D
┏
G
F
●B
●C
●A
●O
┓
D
┏
G
F
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
A.E、F、G B.F、G、H C.G、H、E D.H、E、F
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:三角形的外接圆及外心
问题提出:已知△ABC,用直尺和圆规作出过点A,B,C的圆.
A
B
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
N
M
F
E
A
B
C
作法:
1.作线段AB的垂直平分线MN;
2.作线段AC的垂直平分线EF,交MN于点O;
3.连接OB.
4.以O为圆心,OB为半径作圆.
⊙O就是所求作的圆.
合作探究
当堂检测
学习目标
课堂总结
自主学习
揭示概念:
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
三角形的外接圆
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况
锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
小结:
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.下列命题不正确的是( )
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,A,B是已知圆上两点,用直尺和圆规作以AB为底边的圆内接等腰三角形.这样的三角形能作几个?
解:能作2个.作AB的垂直平分线与圆有两个交点,则得到相应的两个等腰三角形,如图:
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
确定圆的条件
1.确定圆的条件:不在同一条直线的三点共圆
2.三角形的外接圆:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
