1.5 三角函数的应用 课件(共18张PPT) 2023-2024学年初中数学北师版九年级下册
文档属性
| 名称 | 1.5 三角函数的应用 课件(共18张PPT) 2023-2024学年初中数学北师版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 772.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:43:58 | ||
图片预览



文档简介
(共18张PPT)
第一章 直角三角形的边角关系
1.5 三角函数的应用
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.利用解直角三角形知识解决实际问题(重点)
2.能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明
合作探究
当堂检测
学习目标
课堂总结
自主学习
复习回顾:
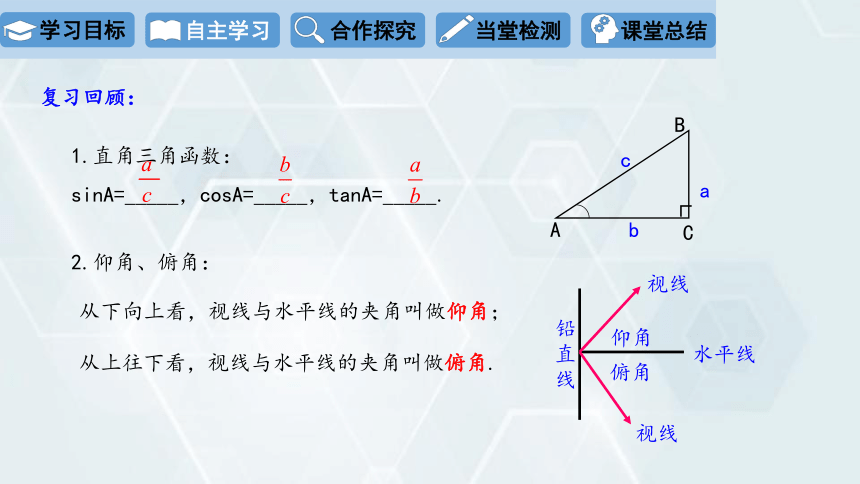
1.直角三角函数:
sinA=_____,cosA=_____,tanA=_____.
b
A
B
C
a
┌
c
铅直线
水平线
视线
视线
仰角
俯角
从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
2.仰角、俯角:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:与方向角有关的实际问题
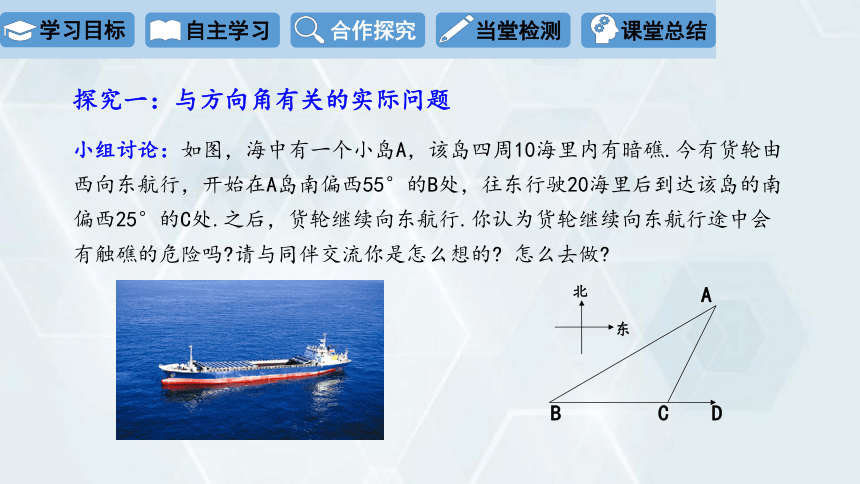
小组讨论:如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗 请与同伴交流你是怎么想的 怎么去做
A
B
C
D
北
东
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究:
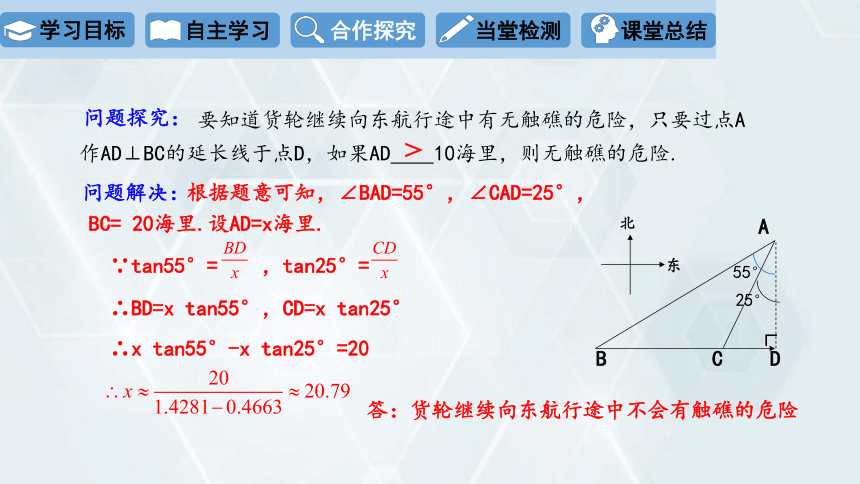
要知道货轮继续向东航行途中有无触礁的危险,只要过点A作AD⊥BC的延长线于点D,如果AD 10海里,则无触礁的危险.
>
A
B
C
D
北
东
┌
55°
25°
问题解决:
根据题意可知,∠BAD=55°,∠CAD=25°,BC= 20海里.设AD=x海里.
∴BD=x tan55°,CD=x tan25°
∴x tan55°-x tan25°=20
∵tan55°= ,tan25°=
答:货轮继续向东航行途中不会有触礁的危险
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40 海里 B.40 海里
C.80海里 D.40 海里
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:与仰角、俯角相关的测量与计算
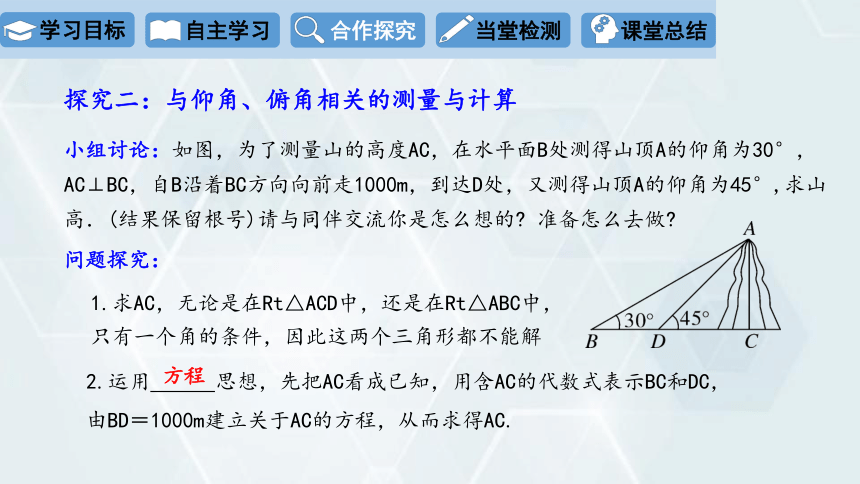
小组讨论:如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)请与同伴交流你是怎么想的 准备怎么去做
问题探究:
1.求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解
2.运用 思想,先把AC看成已知,用含AC的代数式表示BC和DC,
由BD=1000m建立关于AC的方程,从而求得AC.
方程
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
问题解决:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
2.如图,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200米,点C在BD上,则树高AB等于 (根号保留).
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究三:利用坡角解决实际问题
小组讨论:某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 请与同伴交流你是怎么想的 准备怎么去做
小提示:
可以将实际问题转化成数学问题,再解决.
问题探究:
转化问题:
如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.
求(1)AB-BD的长.(2)AD的长.
A
B
C
D
┌
4m
35°
40°
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.求:(1)AB-BD的长.
问题解决:
解:∵sin40°= ,BC=BDsin40°
∵sin35°=
∴AB=
∴AB-BD≈4.48-4=0.48(m)
答:调整后的楼梯会加长约0.48m.
A
B
C
D
┌
4m
35°
40°
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.求:(2) AD的长.
A
B
C
D
┌
4m
35°
40°
解:∵tan40°= ,∴DC=
答:楼梯多占约0.61m的地面.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长5m的竹竿AC斜靠在石坝旁,量出杆长1m处的D点离地面的高度DE=0.6m,又量得杆底与坝脚的距离AB=3m,则石坝的坡度为( )
B
A. B. 3 C. D.4
练一练:
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
用三角函数知识解决实际问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为1:2的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( )
A.4m B. m C. m D.8m
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.某日,一架直升飞机前往救援一艘刚在南海巡航的渔政船.当飞机到达距离海面3 000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
解:在Rt△CDA中,∵∠ACD=30°,CD=3 000米,
∴AD=CDtan∠ACD=1000 (米),
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000 (米),
∴AB=BD-AD=2000 (米).
答:此时渔政船和渔船相距2000 米.
3.如图,亿隆小区内有一条南北方向的小路MN,某快递员从小路旁的A处出发沿南偏东53°方向行走258m将快递送至B楼,又继续从B楼沿南偏西30°方向行走172m将快递送至C楼,求此时快递员到小路MN的距离.(计算结果精确到1m.)
解:过B作BD⊥MN于D,过C作CE⊥MN于E,过B作BF⊥EC于F,则四边形DEFB是矩形,∴BD=EF,
在Rt△ABD中,∠ADB=90°,∠DAB=53°,AB=258m,
∴BD=AB sin53°=258×0.8=206.4,
在Rt△BCF中,∠BFC=90°,∠CBF=30°,BC=172,
∴CF= BC=86,∴CE=EF﹣CF=BD﹣CF=206.4﹣86=120.4m,
答:快递员到小路MN的距离是120.4m.
D
E
F
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
三角函数的应用
用三角函数知识解决实际问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
第一章 直角三角形的边角关系
1.5 三角函数的应用
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.利用解直角三角形知识解决实际问题(重点)
2.能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明
合作探究
当堂检测
学习目标
课堂总结
自主学习
复习回顾:
1.直角三角函数:
sinA=_____,cosA=_____,tanA=_____.
b
A
B
C
a
┌
c
铅直线
水平线
视线
视线
仰角
俯角
从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
2.仰角、俯角:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:与方向角有关的实际问题
小组讨论:如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗 请与同伴交流你是怎么想的 怎么去做
A
B
C
D
北
东
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究:
要知道货轮继续向东航行途中有无触礁的危险,只要过点A作AD⊥BC的延长线于点D,如果AD 10海里,则无触礁的危险.
>
A
B
C
D
北
东
┌
55°
25°
问题解决:
根据题意可知,∠BAD=55°,∠CAD=25°,BC= 20海里.设AD=x海里.
∴BD=x tan55°,CD=x tan25°
∴x tan55°-x tan25°=20
∵tan55°= ,tan25°=
答:货轮继续向东航行途中不会有触礁的危险
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40 海里 B.40 海里
C.80海里 D.40 海里
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:与仰角、俯角相关的测量与计算
小组讨论:如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)请与同伴交流你是怎么想的 准备怎么去做
问题探究:
1.求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解
2.运用 思想,先把AC看成已知,用含AC的代数式表示BC和DC,
由BD=1000m建立关于AC的方程,从而求得AC.
方程
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
问题解决:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
2.如图,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200米,点C在BD上,则树高AB等于 (根号保留).
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究三:利用坡角解决实际问题
小组讨论:某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 请与同伴交流你是怎么想的 准备怎么去做
小提示:
可以将实际问题转化成数学问题,再解决.
问题探究:
转化问题:
如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.
求(1)AB-BD的长.(2)AD的长.
A
B
C
D
┌
4m
35°
40°
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.求:(1)AB-BD的长.
问题解决:
解:∵sin40°= ,BC=BDsin40°
∵sin35°=
∴AB=
∴AB-BD≈4.48-4=0.48(m)
答:调整后的楼梯会加长约0.48m.
A
B
C
D
┌
4m
35°
40°
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.求:(2) AD的长.
A
B
C
D
┌
4m
35°
40°
解:∵tan40°= ,∴DC=
答:楼梯多占约0.61m的地面.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长5m的竹竿AC斜靠在石坝旁,量出杆长1m处的D点离地面的高度DE=0.6m,又量得杆底与坝脚的距离AB=3m,则石坝的坡度为( )
B
A. B. 3 C. D.4
练一练:
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
用三角函数知识解决实际问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为1:2的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( )
A.4m B. m C. m D.8m
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.某日,一架直升飞机前往救援一艘刚在南海巡航的渔政船.当飞机到达距离海面3 000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
解:在Rt△CDA中,∵∠ACD=30°,CD=3 000米,
∴AD=CDtan∠ACD=1000 (米),
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000 (米),
∴AB=BD-AD=2000 (米).
答:此时渔政船和渔船相距2000 米.
3.如图,亿隆小区内有一条南北方向的小路MN,某快递员从小路旁的A处出发沿南偏东53°方向行走258m将快递送至B楼,又继续从B楼沿南偏西30°方向行走172m将快递送至C楼,求此时快递员到小路MN的距离.(计算结果精确到1m.)
解:过B作BD⊥MN于D,过C作CE⊥MN于E,过B作BF⊥EC于F,则四边形DEFB是矩形,∴BD=EF,
在Rt△ABD中,∠ADB=90°,∠DAB=53°,AB=258m,
∴BD=AB sin53°=258×0.8=206.4,
在Rt△BCF中,∠BFC=90°,∠CBF=30°,BC=172,
∴CF= BC=86,∴CE=EF﹣CF=BD﹣CF=206.4﹣86=120.4m,
答:快递员到小路MN的距离是120.4m.
D
E
F
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
三角函数的应用
用三角函数知识解决实际问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
