5.3 简单的轴对称现象(第1课时) 课件(共37张PPT)
文档属性
| 名称 | 5.3 简单的轴对称现象(第1课时) 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览










文档简介
(共37张PPT)
5.3 简单的轴对称现象
第1课时
1.探索并掌握等腰三角形的轴对称性及其相关性质.
2.通过探索简单图形轴对称的过程,进一步体验轴对称的特征,发展空间观念.
3.通过学生的操作与思考,使学生掌握等腰三角形和等边三角形的轴对称性及其有关性质,从而发展空间观念.
教学重点:掌握等腰三角形的轴对称性及其相关性质.
教学难点:探索等腰三角形的轴对称性及其性质的过程.
轴对称
图形
两个图形
成轴对称
轴对称
定义:一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合.
定义:一个图形沿一条直线折叠,如果它能够与另一个图形重合
特征:一个图形具有的特殊形状
特征:两个全等图形的特殊的位置关系
互相转化
性质:在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等。
轴对称
的性质
观察下列图片,它们有什么共同的特征?
等腰三角形
有两条边相等的三角形叫做等腰三角形。
A
B
C
顶角
腰
腰
底边
底角
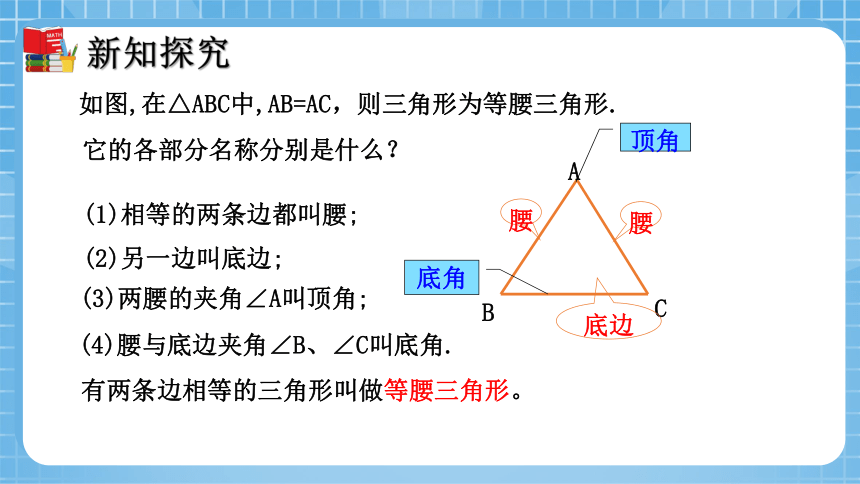
如图,在△ABC中,AB=AC,则三角形为等腰三角形.
它的各部分名称分别是什么?
(1)相等的两条边都叫腰;
(2)另一边叫底边;
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角.
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
你是如何得到问题的答案的?
直接想象
折叠操作
折叠验证
想象过程
找出等腰△ABC的对称轴.
等腰三角形底边的中线所在的直线.
等腰三角形底边的高所在的直线.
你同意他们的观点吗?
把等腰三角形沿折痕AD对折后,左右两边重合,所以等腰三角形是轴对称图形;
重合的线段:
AB=AC
BD=CD
∠BAD=∠CAD
重合的角:
B
A
C
D
其中重合的线段和重合的角有:
1
2
4
3
∠ADB=∠ADC
∠B=∠C
( ∠1=∠2 )
( ∠3=∠4 )
B
A
C
D
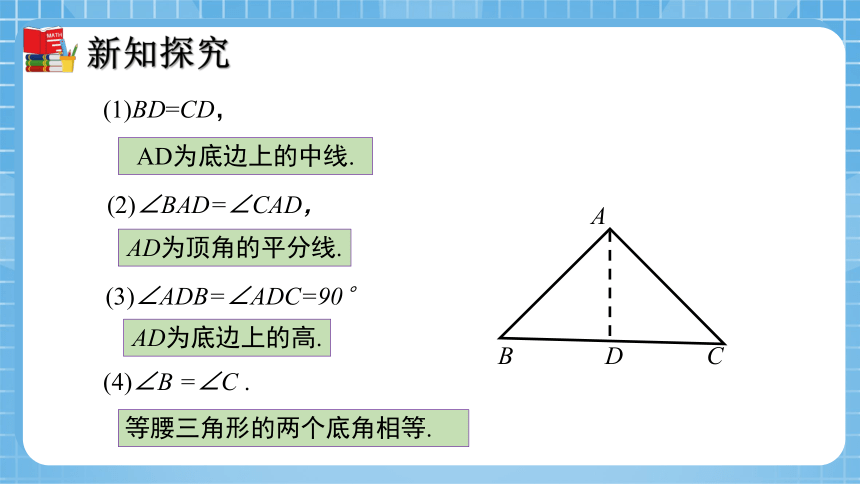
(1)BD=CD,
AD为底边上的中线.
(2)∠BAD=∠CAD,
AD为顶角的平分线.
(3)∠ADB=∠ADC=90°
AD为底边上的高.
(4)∠B =∠C .
等腰三角形的两个底角相等.
1.等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD是∠BAC的平分线,求证:直线AD是等腰△ABC的对称轴.
证明:∵AD是∠BAC的平分线,
∴∠BAD=∠ CAD.
在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴直线AD是等腰△ABC的对称轴.
A
B
C
D
证明:∵AD是△ABC的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴直线AD是等腰△ABC的对称轴.
2.等腰三角形底边上的中线所在的直线是它的对称轴.
如图,在等腰△ABC中,AB=AC,AD是△ABC的中线.求证:直线AD是等腰△ABC的对称轴.
3.等腰三角形底边上的高所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:直线AD是等腰△ABC的对称轴.
证明:∵AD⊥BC,
∴∠BDA=∠CDA=90°.
∴直线AD是等腰△ABC的对称轴.
在△ABD和△ACD中,
AB=AC
AD=AD,
∴△ABD≌△ACD(HL).
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
证明: 在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴BD=CD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,∠BAD=∠ CAD.
求证:AD⊥BC,BD=CD.
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
证明: 在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,BD=CD.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
证明:∵AD⊥BC,
∴∠BDA=∠CDA=90°.
在Rt△ABD和Rt△ACD中,
AB=AC
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∴∠BAD=∠CAD,
BD= CD.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
“知其一”,
“得另二”!
A
B
C
D
在△ABC中,AB=AC,
∵AD⊥BC,∴∠BAD=∠CAD,BD=CD.
在△ABC中,AB=AC,
∵∠BAD=∠CAD,∴AD⊥BC,BD=CD.
在△ABC中,AB=AC,
∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
等腰三角形的两个底角相等.
在△ABC中,
∵AB=AC,
∴∠B=∠C.
几何语言:
A
B
C
D
简称为:“等边对等角”.
例1.如图,已知屋架的顶角∠BAC=100°,立柱AD垂直于横梁BC,斜梁AB=AC.求∠B,∠C,∠BAD,∠CAD.
解:因为AB=AC,∠BAC=100°,AD⊥BC,
所以∠B=∠C=40°,
∠BAD=∠CAD=50°.
(1) 等边三角形有几条对称轴?
(2) 你能发现它的哪些特征?
有3条对称轴
等边三角形的三条边都相等;
等边三角形的内角都相等,且等于 60 °;
等边三角形是轴对称图形,有三条对称;
等边三角形各边上中线,高和所对角的平分线都三线合一.
等边三角形是轴对称图形,共有三条对称轴。
等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”),它们所在的直线都是等边三角形的对称轴。
等边三角形的各角都相等,都等于60°
A
C
B
解:因为AB=AC, BD=BC=AD,(已知)
所以∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,因为∠A+∠ABD+∠ADB=180°,
又因为∠BDC+∠ADB=180°,所以∠BDC=∠A+∠ABD=2x°.
因为∠ABC=∠C=∠BDC=2x°,
所以x+2x+2x=180.(三角形内角和等于180°)
解得 x=36.所以∠A=36°,∠C=72°.
例2.如图,在ΔABC中,AB=AC , 点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
C
D
B
A
你有哪些办法可以得到一个等腰三角形?与同伴交流.
1.按下面的步骤做一做:
(1)将长方形纸片对折
(2)然后沿对角线折叠,在沿折痕剪开.
解:因为OA=AB,
所以∠ABO=∠O=15°,所以∠BAO=150°,
所以∠BAC=∠ABO+∠O=30°.
因为AB=BC,
所以∠ACB=∠BAC=30°,
所以∠CBO=135°,所以∠CBD=∠O+∠ACB=45°.
因为BC=CD,所以∠D=∠CBD=45°,所以∠BCD=90°,
所以∠1=180°-∠BCD-∠BCO=60°.
例3.如图,∠AOB=15°,且OA=AB=BC=CD.求∠1的度数.
⌒
15°
1
C
D
B
O
A
⌒
1.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35°
C.40° D.70°
B
2.一个等边三角形的对称轴共有 ( )
A.1条 B.2条 C.3条 D.6条
3. 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )
A.36° B.54°
C.18° D.64°
B
4.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB
于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;
②AD上任意一点到AB,AC的距离相等;③BD=CD;
④若点P在直线AD上,则PB=PC.
其中正确的是( )
A.① B.①②
C.①②③ D.①②③④
D
5.在△ABC 中,AB = AC.
(1)若∠A = 40°,则∠C 等于多少度?
(2)若∠B = 72°,则∠A 等于多少度?
A
B
C
6.填空:
(1)等腰直角三角形的每一个锐角的度数是 ;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是______ ;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于____________ ;
20°或50°
100°
45°
7.如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M. 试说明:CM=MD.
解:如图,连接AC,AD.
在△ABC和△AED中,
所以△ABC≌△AED(SAS).
所以AC=AD.
又因为AM⊥CD,
所以CM=MD.
8.如图,∠AOB=15°,且OA=AB=BC=CD.求∠1的度数.
⌒
15°
1
C
D
B
O
A
⌒
9.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)试说明:△ABE≌△DCE;
(2)求∠AED的度数.
(2).由(1)可知AB=BE,∠ABE=30°,
所以∠BAE=∠BEA=75°.
同理,∠CDE=∠CED=75°.
所以∠AED=360°-75°-75°-60°=150°.
等腰三角形的性质
轴对称图形
等腰三角形
三线合一
等边对等角
等边三角形的性质
三线合一
轴对称图形
各角都相等
,都为60度
习题5.3
第1、2题
5.3 简单的轴对称现象
第1课时
1.探索并掌握等腰三角形的轴对称性及其相关性质.
2.通过探索简单图形轴对称的过程,进一步体验轴对称的特征,发展空间观念.
3.通过学生的操作与思考,使学生掌握等腰三角形和等边三角形的轴对称性及其有关性质,从而发展空间观念.
教学重点:掌握等腰三角形的轴对称性及其相关性质.
教学难点:探索等腰三角形的轴对称性及其性质的过程.
轴对称
图形
两个图形
成轴对称
轴对称
定义:一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合.
定义:一个图形沿一条直线折叠,如果它能够与另一个图形重合
特征:一个图形具有的特殊形状
特征:两个全等图形的特殊的位置关系
互相转化
性质:在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等。
轴对称
的性质
观察下列图片,它们有什么共同的特征?
等腰三角形
有两条边相等的三角形叫做等腰三角形。
A
B
C
顶角
腰
腰
底边
底角
如图,在△ABC中,AB=AC,则三角形为等腰三角形.
它的各部分名称分别是什么?
(1)相等的两条边都叫腰;
(2)另一边叫底边;
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角.
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
你是如何得到问题的答案的?
直接想象
折叠操作
折叠验证
想象过程
找出等腰△ABC的对称轴.
等腰三角形底边的中线所在的直线.
等腰三角形底边的高所在的直线.
你同意他们的观点吗?
把等腰三角形沿折痕AD对折后,左右两边重合,所以等腰三角形是轴对称图形;
重合的线段:
AB=AC
BD=CD
∠BAD=∠CAD
重合的角:
B
A
C
D
其中重合的线段和重合的角有:
1
2
4
3
∠ADB=∠ADC
∠B=∠C
( ∠1=∠2 )
( ∠3=∠4 )
B
A
C
D
(1)BD=CD,
AD为底边上的中线.
(2)∠BAD=∠CAD,
AD为顶角的平分线.
(3)∠ADB=∠ADC=90°
AD为底边上的高.
(4)∠B =∠C .
等腰三角形的两个底角相等.
1.等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD是∠BAC的平分线,求证:直线AD是等腰△ABC的对称轴.
证明:∵AD是∠BAC的平分线,
∴∠BAD=∠ CAD.
在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴直线AD是等腰△ABC的对称轴.
A
B
C
D
证明:∵AD是△ABC的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴直线AD是等腰△ABC的对称轴.
2.等腰三角形底边上的中线所在的直线是它的对称轴.
如图,在等腰△ABC中,AB=AC,AD是△ABC的中线.求证:直线AD是等腰△ABC的对称轴.
3.等腰三角形底边上的高所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:直线AD是等腰△ABC的对称轴.
证明:∵AD⊥BC,
∴∠BDA=∠CDA=90°.
∴直线AD是等腰△ABC的对称轴.
在△ABD和△ACD中,
AB=AC
AD=AD,
∴△ABD≌△ACD(HL).
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
证明: 在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴BD=CD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,∠BAD=∠ CAD.
求证:AD⊥BC,BD=CD.
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
证明: 在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,BD=CD.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
证明:∵AD⊥BC,
∴∠BDA=∠CDA=90°.
在Rt△ABD和Rt△ACD中,
AB=AC
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∴∠BAD=∠CAD,
BD= CD.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
“知其一”,
“得另二”!
A
B
C
D
在△ABC中,AB=AC,
∵AD⊥BC,∴∠BAD=∠CAD,BD=CD.
在△ABC中,AB=AC,
∵∠BAD=∠CAD,∴AD⊥BC,BD=CD.
在△ABC中,AB=AC,
∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
等腰三角形的两个底角相等.
在△ABC中,
∵AB=AC,
∴∠B=∠C.
几何语言:
A
B
C
D
简称为:“等边对等角”.
例1.如图,已知屋架的顶角∠BAC=100°,立柱AD垂直于横梁BC,斜梁AB=AC.求∠B,∠C,∠BAD,∠CAD.
解:因为AB=AC,∠BAC=100°,AD⊥BC,
所以∠B=∠C=40°,
∠BAD=∠CAD=50°.
(1) 等边三角形有几条对称轴?
(2) 你能发现它的哪些特征?
有3条对称轴
等边三角形的三条边都相等;
等边三角形的内角都相等,且等于 60 °;
等边三角形是轴对称图形,有三条对称;
等边三角形各边上中线,高和所对角的平分线都三线合一.
等边三角形是轴对称图形,共有三条对称轴。
等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”),它们所在的直线都是等边三角形的对称轴。
等边三角形的各角都相等,都等于60°
A
C
B
解:因为AB=AC, BD=BC=AD,(已知)
所以∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,因为∠A+∠ABD+∠ADB=180°,
又因为∠BDC+∠ADB=180°,所以∠BDC=∠A+∠ABD=2x°.
因为∠ABC=∠C=∠BDC=2x°,
所以x+2x+2x=180.(三角形内角和等于180°)
解得 x=36.所以∠A=36°,∠C=72°.
例2.如图,在ΔABC中,AB=AC , 点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
C
D
B
A
你有哪些办法可以得到一个等腰三角形?与同伴交流.
1.按下面的步骤做一做:
(1)将长方形纸片对折
(2)然后沿对角线折叠,在沿折痕剪开.
解:因为OA=AB,
所以∠ABO=∠O=15°,所以∠BAO=150°,
所以∠BAC=∠ABO+∠O=30°.
因为AB=BC,
所以∠ACB=∠BAC=30°,
所以∠CBO=135°,所以∠CBD=∠O+∠ACB=45°.
因为BC=CD,所以∠D=∠CBD=45°,所以∠BCD=90°,
所以∠1=180°-∠BCD-∠BCO=60°.
例3.如图,∠AOB=15°,且OA=AB=BC=CD.求∠1的度数.
⌒
15°
1
C
D
B
O
A
⌒
1.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35°
C.40° D.70°
B
2.一个等边三角形的对称轴共有 ( )
A.1条 B.2条 C.3条 D.6条
3. 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )
A.36° B.54°
C.18° D.64°
B
4.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB
于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;
②AD上任意一点到AB,AC的距离相等;③BD=CD;
④若点P在直线AD上,则PB=PC.
其中正确的是( )
A.① B.①②
C.①②③ D.①②③④
D
5.在△ABC 中,AB = AC.
(1)若∠A = 40°,则∠C 等于多少度?
(2)若∠B = 72°,则∠A 等于多少度?
A
B
C
6.填空:
(1)等腰直角三角形的每一个锐角的度数是 ;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是______ ;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于____________ ;
20°或50°
100°
45°
7.如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M. 试说明:CM=MD.
解:如图,连接AC,AD.
在△ABC和△AED中,
所以△ABC≌△AED(SAS).
所以AC=AD.
又因为AM⊥CD,
所以CM=MD.
8.如图,∠AOB=15°,且OA=AB=BC=CD.求∠1的度数.
⌒
15°
1
C
D
B
O
A
⌒
9.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)试说明:△ABE≌△DCE;
(2)求∠AED的度数.
(2).由(1)可知AB=BE,∠ABE=30°,
所以∠BAE=∠BEA=75°.
同理,∠CDE=∠CED=75°.
所以∠AED=360°-75°-75°-60°=150°.
等腰三角形的性质
轴对称图形
等腰三角形
三线合一
等边对等角
等边三角形的性质
三线合一
轴对称图形
各角都相等
,都为60度
习题5.3
第1、2题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
