2024普通高中学业水平考试数学模拟卷1(含解析)
文档属性
| 名称 | 2024普通高中学业水平考试数学模拟卷1(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:25:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024普通高中学业水平考试数学模拟卷(一)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知全集U={2,4,6,8,10},集合A={2,4},B={1,6,8},则( UA)∩B=( )
A.{2,4} B.{6,8,10} C.{6,8} D.{2,4,6,8,10}
2.函数f(x)=log2(x+3)+(x+2)0的定义域是( )
A.[-3,+∞) B.(-3,-2)∪(-2,+∞) C.(-3,+∞) D.[-3,2)∪(2,+∞)
3.设x∈R,则“|x-1|<1”是“x2<2x”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知一个圆柱的侧面展开图内切圆的半径为1,则该圆柱的体积为( )
A. B. C.8π D.π
5.在△ABC中,内角A,B,C所对的边分别为a,b,c,若c(sin B-1)=b-c,则角C为( )
A. B. C. D.
6.下列说法正确的是( )
A.一个平面里有三个不同的点到另一个平面的距离都相等,则这两个平面平行
B.和同一条直线都相交的两条直线一定相交
C.经过空间中三个点有且只有一个平面
D.经过两条相交直线有且只有一个平面
7.函数f(x)=的大致图象是( )
8.已知点(2,-2)在角α的终边上,则角α的最小正值为( )
A. B. C. D.
9.正实数x,y满足2x+3y=1,则的最小值是( )
A.3 B.7 C.10+4 D.10+
10.已知函数y=f(x)的定义域是R,值域为[-2,8],则下列函数中值域也为[-2,8]的是( )
A.y=3f(x)+1 B.y=f(3x+1) C.y=-f(x) D.y=|f(2x)|
11.在下列说法中,正确的是( )
A.第三象限角大于第二象限角 B.若P(2a,a)(a≠0)是角α终边上一点,则cos α=
C.若α,β的终边不相同,则cos α≠cos β D.tan x=-的解集为xx=kπ-,k∈Z
12.已知函数f(x)=则函数F(x)=f[f(x)]-2f(x)-的零点个数是( )
A.2 B.3
C.4 D.5
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.已知i是虚数单位,z1=1-i,复数z2是z1的共轭复数,则下列结论正确的有( )
A.z1+z2=2 B.z1·z2=2
C.z1>z2 D.=-i
14.给定数6,4,3,6,3,8,8,3,1,8,则这组数据的( )
A.中位数为5 B.方差为
C.平均数为5 D.85%分位数为8
15.已知向量a=(2,1),b=(-6,2),c=,-,则下列说法正确的有( )
A.a·b=-6
B.向量a在向量b上的投影向量为-b
C.(a+b)⊥(a-b)
D.a⊥c
16.已知f(x)=sin2x++2cos(2x+φ)且f(0)=f,-≤φ≤,则下列说法正确的有( )
A.f(x)的图象的一条对称轴方程为x=
B.当x∈0,时f(x)的取值范围为[-3,3]
C.f(x)的图象可由g(x)=3sin 2x的图象向左平移个单位长度得到
D.f(x)的图象的一个对称中心为-,0
三、填空题(本大题共4小题,共15分)
17.在△ABC中,A=,cos B=,AB=2,sin C= ,AC= .
18.已知函数f(x)=的值域为R,则实数a的取值范围是 .
19.在矩形ABCD中,AB=6,AD=2,点M,N满足=2,则= .
20. 在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是2,且所在的平面互相垂直.可以滚动的弹珠M,N分别从A,F出发沿对角线AC,FB匀速移动,已知弹珠N的速度是弹珠M的速度的3倍,且当弹珠N移动到B处时试验终止,则弹珠M,N间的最短距离是 .
四、解答题(本大题共3小题,共33分)
21.(11分)某公司有甲、乙两个研发小组,它们研发一种芯片需要两道工序,第一道工序成功的概率分别为,第二道工序成功的概率分别为.根据生产需要现安排甲小组研发芯片A,乙小组研发芯片B,假设两个小组的研发相互独立.
(1)求两种芯片都研发成功的概率;
(2)政府为了提高该公司研发的积极性,决定只要有芯片研发成功就奖励该公司500万元,求该公司获得政府奖励的概率.
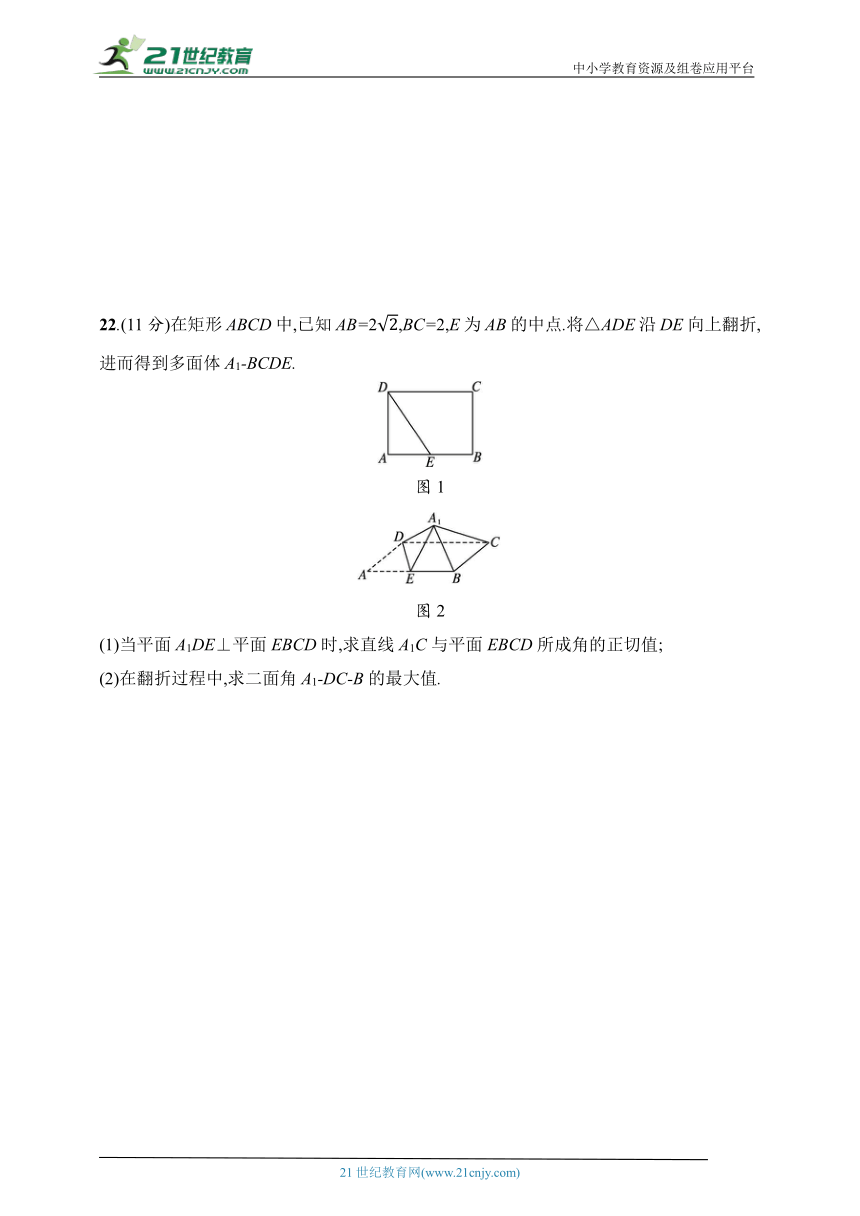
22.(11分)在矩形ABCD中,已知AB=2,BC=2,E为AB的中点.将△ADE沿DE向上翻折,进而得到多面体A1-BCDE.
图1
图2
(1)当平面A1DE⊥平面EBCD时,求直线A1C与平面EBCD所成角的正切值;
(2)在翻折过程中,求二面角A1-DC-B的最大值.
23.(11分)已知函数f(x)=x|x-a|+x,a∈R.
(1)若a=0,判断函数f(x)的奇偶性(不需要给出证明);
(2)若函数f(x)在R上是增函数,求实数a的取值范围;
(3)若存在实数a∈[-2,3],使得关于x的方程f(x)-tf(a)=0有三个不相等的实数根,求实数t的取值范围.
普通高中学业水平考试数学模拟卷(一)
1.C 解析 因为全集U={2,4,6,8,10},集合A={2,4},所以 UA={6,8,10},因为B={1,6,8},所以( UA)∩B={6,8},故选C.
2.B 解析 由题意知,所以x>-3且x≠-2,故函数f(x)的定义域为(-3,-2)∪(-2,+∞).故选B.
3.C 解析 由|x-1|<1得04.A 解析 设圆柱的底面圆半径为r,高为h,由侧面展开图的内切圆半径为1可知h=2,2πr=2,即r=,所以圆柱的体积为πr2h=π2×2=,故选A.
5.B 解析 ∵c(sin B-1)=b-c,∴csin B=b,
∴sin Csin B=sin B,由角B为三角形内角,得sin B≠0,∴sin C=,由06.D 解析 对于A,一个平面里有三个不同的点到另一个平面的距离都相等,此三点不共线时两平面才平行,若三点共线,则这两个平面可能相交也可能平行,故A错误;
对于B,和同一条直线都相交的两条直线不一定相交,也可能平行或异面,故B错误;
对于C,经过空间中三个不共线的点有且只有一个平面,故C错误;
对于D,两条相交直线可以确定一个平面,故D正确.故选D.
7.A 解析 因为f(x)=的定义域为R,且f(-x)==-f(x),所以函数为奇函数,故其图象关于原点对称,故B,C错误;
当x趋向正无穷时,显然f(x)=的分子增长远快于分母增长,y趋向正无穷,故A正确,D错误.故选A.
8.A 解析 由题意可知角α的终边在第四象限,且tan α==-,所以α=-+2kπ,k∈Z,故当k=1时α取最小正值,此时α=.故选A.
9.C 解析 由2x+3y=1,得3y=1-2x,所以=(2x+3y)-=10+,由于x,y为正数,所以10+≥2+10=4+10,当且仅当,即y=,x=时等号成立,故选C.
10.B 解析 因为f(x)的定义域为R,值域为[-2,8],所以y=3f(x)+1的值域为[-5,25],y=-f(x)的值域为[-8,2],y=|f(2x)|的值域为[0,8],y=f(3x+1)的值域为[-2,8],故选B.
11.D 解析 对于A,当α=-150°,β=120°时,α,β分别为第三象限,第二象限的角,但是α<β,故A错误;
对于B,cos α=,故B错误;
对于C,当α=-β+2kπ,k∈Z时,cos α=cos β,故C错误;
对于D,tan x=-得x=kπ-,k∈Z,所以D正确.
故选D.
12.B 解析 设f(x)=t,则F(x)=f[f(x)]-2f(x)-=f(t)-2t-,令F(x)=0,即f(t)-2t-=0,即f(t)=2t+.
在同一个平面直角坐标系中,画出y=f(t)与y=2t+的图象如图所示.
由图象可知,f(t)-2t-=0的两个解t1=0,t2∈(2,3),函数f(x)=t1=0有一个解,f(x)=t2∈(2,3)有两个解,故F(x)=f[f(x)]-2f(x)-的零点个数是3.故选B.
13.ABD 解析 因为z1=1-i,复数z2是z1的共轭复数,所以z2=1+i,所以z1+z2=1-i+1+i=2,故A正确;
z1·z2=(1-i)·(1+i)=12-i2=2,故B正确;
因为虚数不能比较大小,故C错误;
=-i,故D正确.故选ABD.
14.ACD 解析 将数6,4,3,6,3,8,8,3,1,8按从小到大的顺序排列,得1,3,3,3,4,6,6,8,8,8,则这组数据的中位数为=5,故A正确;
平均数为=5,故C正确;
则方差为×[(1-5)2+(4-5)2+(3-5)2×3+(8-5)2×3+(6-5)2×2]=5.8,故B错误;
因为10×85%=8.5,所以85%分位数是从小到大第9个数字,为8,故D正确,故选ACD.
15.BD 解析 因为a=(2,1),b=(-6,2),c=,-,
所以a·b=-12+2=-10≠-6,故A错误;
向量a在向量b上的投影向量为=-b=-b,故B正确;
因为a+b=(-4,3),a-b=(8,-1),
所以(a+b)·(a-b)=-32-3=-35≠0,故C错误;
因为a·c=2×=0,所以a⊥c,故D正确.故选BD.
16.AD 解析 因为f(x)=sin2x++2cos(2x+φ)且f(0)=f,所以sin+2cos φ=sin+2cos+φ,即2cos φ=2coscos φ-2sinsin φ,所以tan φ=-,
因为-≤φ≤,所以φ=-,
所以f(x)=sin2x++2cos2x-=sin2x++2cos2x+-=3sin2x+,
因为f=3sin2×=3sin=3,
所以f(x)的图象的一条对称轴方程为x=,故A正确;
当x∈0,时,2x+∈,所以sin2x+∈-,1,则f(x)∈-,3,故B错误;
将g(x)=3sin 2x的图象向左平移个单位长度得到y=3sin 2x+=3sin2x+的图象,故C错误;
因为f-=3sin-2×=3sin 0=0,所以f(x)的图象的一个对称中心为-,0,故D正确.故选AD.
17. 解析 ∵cos B=,B为三角形内角,
∴sin B=,
∴sin C=sin[π-(A+B)]=sin(A+B)=sincos B+cossin B=.
由正弦定理可得,即AC=.
18.(-∞,4] 解析 当-1当x>0时,若a=0,则f(x)=x-4,单调递增,所以f(x)>-4,此时f(x)=的值域为R,符合题意;
若a<0,则f(x)=x+-4单调递增,所以f(x)在(0,+∞)内的取值范围为R,所以a<0满足题意;
若a>0,则当x>时,f(x)单调递增,当00时,f(x)min=f()=2-4,要使得f(x)值域为R,则要满足2-4≤0,解得0综上,实数a的取值范围是(-∞,4].
19. 14 解析 +,所以·=×36=14.
20. 解析 过点M作MH垂直AB于点H,连接NH,如图所示,因为平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,MH在平面ABCD内,MH⊥AB,则MH⊥平面ABEF,NH 平面ABEF,所以MH⊥NH.
由已知弹珠N的速度是弹珠M的速度的3倍,设AM=a,则NF=3a0≤a≤,因为四边形ABCD,ABEF为正方形,AB=2,则AC=BF=2,∠ABF=∠CAB=45°,所以MH=AH=a,所以BH=2-a,BN=2-3a,在△BHN中,由余弦定理可得|NH|2=|BH|2+|BN|2-2|BH|·|BN|cos 45°=2-a2+(2-3a)2-22-a(2-3a)·=4-2a+a2+8-12a+9a2-(2-a)(2-3a)=4-6a+a2,
所以|MN|2=|MH|2+|NH|2=7a2-6a+40≤a≤,
当a=时,|MN,所以|MN|min=.
21.解 (1)甲小组研发芯片A成功的概率为p1=,乙小组研发芯片B成功的概率为p2=,由于两个小组的研发相互独立,所以A,B两种芯片研发都成功的概率P1=p1·p2=.
(2)该公司获得政府奖励则需有芯片研发成功,根据对立事件可知获奖的概率为P2=1-(1-p1)(1-p2)=1-1-×1-=1-.
22.解 (1)在题图1中,连接AC交DE于点F,易知AC=2.
因为,∠DAE=∠ABC=90°,所以△DAE∽△ABC,可得AC⊥DE.
易知△DFC∽△EFA,则AF=,CF=,因为平面A1DE⊥平面EBCD,平面A1DE∩平面EBCD=DE,A1F 平面A1DE,所以A1F⊥平面EBCD.
则∠A1CF是直线A1C与平面EBCD所成角,tan∠A1CF=.
(2)如图,作出A1F,AC,过点A1作A1H⊥FC,垂足为H,过点H作HG⊥DC,垂足为G,连接A1G.
由(1)可知DE⊥CF,DE⊥A1F,CF∩A1F=F,CF,A1F 平面A1FC,则DE⊥平面A1FC,且A1H 平面A1FC,可得A1H⊥DE.
且A1H⊥FC,FC∩DE=F,DE,FC 平面BCDE,所以A1H⊥平面BCDE.
由CD 平面BCDE,可得A1H⊥CD.
又因为HG⊥CD,A1H∩HG=H,A1H,HG 平面A1HG,所以CD⊥平面A1HG,由A1G 平面A1HG,可得CD⊥A1G,所以∠A1GH是二面角A1-CD-B的平面角,设∠A1FC=θ,θ∈(0,π),由(1)可知A1F=,FC=,
在Rt△A1FH中,A1H=sin θ,FH=cos θ,则CH=FC-FH=(2-cos θ),
因为HG⊥DC,则HG∥AD,可得,所以HG=(2-cos θ),
在Rt△A1HG中,tan∠A1GH=.
设y=,θ∈(0,π),则y>0,sin θ+ycos θ=sin(θ+φ)=2y,其中sin φ=,cos φ=,即sin(θ+φ)=≤1,解得0又因为∠A1GH∈(0,π),则0<∠A1GH≤,所以二面角A1-DC-B的最大值为.
23.解 (1)当a=0时,f(x)=x|x|+x,f(-x)=-x|-x|-x=-f(x),所以函数f(x)为奇函数.
(2)f(x)=
函数y=x2+(1-a)x的图象的对称轴为直线x=,函数y=-x2+(a+1)x的图象的对称轴为直线x=.
若函数f(x)在R上是增函数,则≤a≤,解得-1≤a≤1,即a的取值范围是[-1,1].
(3)方程f(x)-tf(a)=0的解即为方程f(x)=tf(a)的解.
①当-1≤a≤1时,函数f(x)在R上是增函数,所以关于x的方程f(x)=tf(a)不可能有三个不相等的实数根;
②当a>1时,即a>,所以函数f(x)在-∞,内单调递增,在,a内单调递减,在(a,+∞)内单调递增,当f(a)1,所以1设h(a)=a++2,存在a∈[-2,3]使得关于x的方程f(x)=tf(a)有三个不相等的实数根,所以1任取a1,a2∈(1,3]且a11,所以h(a1)所以当a∈(1,3]时,h(a)max=,故1③当a<-1时,即a<,函数y=f(x)在(-∞,a)内单调递增,在a,内单调递减,在,+∞内单调递增,当f即-1,所以g(a1)>g(a2),故函数g(a)=-a+-2在[-2,-1)内单调递减.
因为存在a∈[-2,3]使得关于x的方程f(x)=tf(a)有三个不相等的实数根,
所以1综上,t的取值范围为1,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024普通高中学业水平考试数学模拟卷(一)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知全集U={2,4,6,8,10},集合A={2,4},B={1,6,8},则( UA)∩B=( )
A.{2,4} B.{6,8,10} C.{6,8} D.{2,4,6,8,10}
2.函数f(x)=log2(x+3)+(x+2)0的定义域是( )
A.[-3,+∞) B.(-3,-2)∪(-2,+∞) C.(-3,+∞) D.[-3,2)∪(2,+∞)
3.设x∈R,则“|x-1|<1”是“x2<2x”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知一个圆柱的侧面展开图内切圆的半径为1,则该圆柱的体积为( )
A. B. C.8π D.π
5.在△ABC中,内角A,B,C所对的边分别为a,b,c,若c(sin B-1)=b-c,则角C为( )
A. B. C. D.
6.下列说法正确的是( )
A.一个平面里有三个不同的点到另一个平面的距离都相等,则这两个平面平行
B.和同一条直线都相交的两条直线一定相交
C.经过空间中三个点有且只有一个平面
D.经过两条相交直线有且只有一个平面
7.函数f(x)=的大致图象是( )
8.已知点(2,-2)在角α的终边上,则角α的最小正值为( )
A. B. C. D.
9.正实数x,y满足2x+3y=1,则的最小值是( )
A.3 B.7 C.10+4 D.10+
10.已知函数y=f(x)的定义域是R,值域为[-2,8],则下列函数中值域也为[-2,8]的是( )
A.y=3f(x)+1 B.y=f(3x+1) C.y=-f(x) D.y=|f(2x)|
11.在下列说法中,正确的是( )
A.第三象限角大于第二象限角 B.若P(2a,a)(a≠0)是角α终边上一点,则cos α=
C.若α,β的终边不相同,则cos α≠cos β D.tan x=-的解集为xx=kπ-,k∈Z
12.已知函数f(x)=则函数F(x)=f[f(x)]-2f(x)-的零点个数是( )
A.2 B.3
C.4 D.5
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.已知i是虚数单位,z1=1-i,复数z2是z1的共轭复数,则下列结论正确的有( )
A.z1+z2=2 B.z1·z2=2
C.z1>z2 D.=-i
14.给定数6,4,3,6,3,8,8,3,1,8,则这组数据的( )
A.中位数为5 B.方差为
C.平均数为5 D.85%分位数为8
15.已知向量a=(2,1),b=(-6,2),c=,-,则下列说法正确的有( )
A.a·b=-6
B.向量a在向量b上的投影向量为-b
C.(a+b)⊥(a-b)
D.a⊥c
16.已知f(x)=sin2x++2cos(2x+φ)且f(0)=f,-≤φ≤,则下列说法正确的有( )
A.f(x)的图象的一条对称轴方程为x=
B.当x∈0,时f(x)的取值范围为[-3,3]
C.f(x)的图象可由g(x)=3sin 2x的图象向左平移个单位长度得到
D.f(x)的图象的一个对称中心为-,0
三、填空题(本大题共4小题,共15分)
17.在△ABC中,A=,cos B=,AB=2,sin C= ,AC= .
18.已知函数f(x)=的值域为R,则实数a的取值范围是 .
19.在矩形ABCD中,AB=6,AD=2,点M,N满足=2,则= .
20. 在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是2,且所在的平面互相垂直.可以滚动的弹珠M,N分别从A,F出发沿对角线AC,FB匀速移动,已知弹珠N的速度是弹珠M的速度的3倍,且当弹珠N移动到B处时试验终止,则弹珠M,N间的最短距离是 .
四、解答题(本大题共3小题,共33分)
21.(11分)某公司有甲、乙两个研发小组,它们研发一种芯片需要两道工序,第一道工序成功的概率分别为,第二道工序成功的概率分别为.根据生产需要现安排甲小组研发芯片A,乙小组研发芯片B,假设两个小组的研发相互独立.
(1)求两种芯片都研发成功的概率;
(2)政府为了提高该公司研发的积极性,决定只要有芯片研发成功就奖励该公司500万元,求该公司获得政府奖励的概率.
22.(11分)在矩形ABCD中,已知AB=2,BC=2,E为AB的中点.将△ADE沿DE向上翻折,进而得到多面体A1-BCDE.
图1
图2
(1)当平面A1DE⊥平面EBCD时,求直线A1C与平面EBCD所成角的正切值;
(2)在翻折过程中,求二面角A1-DC-B的最大值.
23.(11分)已知函数f(x)=x|x-a|+x,a∈R.
(1)若a=0,判断函数f(x)的奇偶性(不需要给出证明);
(2)若函数f(x)在R上是增函数,求实数a的取值范围;
(3)若存在实数a∈[-2,3],使得关于x的方程f(x)-tf(a)=0有三个不相等的实数根,求实数t的取值范围.
普通高中学业水平考试数学模拟卷(一)
1.C 解析 因为全集U={2,4,6,8,10},集合A={2,4},所以 UA={6,8,10},因为B={1,6,8},所以( UA)∩B={6,8},故选C.
2.B 解析 由题意知,所以x>-3且x≠-2,故函数f(x)的定义域为(-3,-2)∪(-2,+∞).故选B.
3.C 解析 由|x-1|<1得0
5.B 解析 ∵c(sin B-1)=b-c,∴csin B=b,
∴sin Csin B=sin B,由角B为三角形内角,得sin B≠0,∴sin C=,由0
对于B,和同一条直线都相交的两条直线不一定相交,也可能平行或异面,故B错误;
对于C,经过空间中三个不共线的点有且只有一个平面,故C错误;
对于D,两条相交直线可以确定一个平面,故D正确.故选D.
7.A 解析 因为f(x)=的定义域为R,且f(-x)==-f(x),所以函数为奇函数,故其图象关于原点对称,故B,C错误;
当x趋向正无穷时,显然f(x)=的分子增长远快于分母增长,y趋向正无穷,故A正确,D错误.故选A.
8.A 解析 由题意可知角α的终边在第四象限,且tan α==-,所以α=-+2kπ,k∈Z,故当k=1时α取最小正值,此时α=.故选A.
9.C 解析 由2x+3y=1,得3y=1-2x,所以=(2x+3y)-=10+,由于x,y为正数,所以10+≥2+10=4+10,当且仅当,即y=,x=时等号成立,故选C.
10.B 解析 因为f(x)的定义域为R,值域为[-2,8],所以y=3f(x)+1的值域为[-5,25],y=-f(x)的值域为[-8,2],y=|f(2x)|的值域为[0,8],y=f(3x+1)的值域为[-2,8],故选B.
11.D 解析 对于A,当α=-150°,β=120°时,α,β分别为第三象限,第二象限的角,但是α<β,故A错误;
对于B,cos α=,故B错误;
对于C,当α=-β+2kπ,k∈Z时,cos α=cos β,故C错误;
对于D,tan x=-得x=kπ-,k∈Z,所以D正确.
故选D.
12.B 解析 设f(x)=t,则F(x)=f[f(x)]-2f(x)-=f(t)-2t-,令F(x)=0,即f(t)-2t-=0,即f(t)=2t+.
在同一个平面直角坐标系中,画出y=f(t)与y=2t+的图象如图所示.
由图象可知,f(t)-2t-=0的两个解t1=0,t2∈(2,3),函数f(x)=t1=0有一个解,f(x)=t2∈(2,3)有两个解,故F(x)=f[f(x)]-2f(x)-的零点个数是3.故选B.
13.ABD 解析 因为z1=1-i,复数z2是z1的共轭复数,所以z2=1+i,所以z1+z2=1-i+1+i=2,故A正确;
z1·z2=(1-i)·(1+i)=12-i2=2,故B正确;
因为虚数不能比较大小,故C错误;
=-i,故D正确.故选ABD.
14.ACD 解析 将数6,4,3,6,3,8,8,3,1,8按从小到大的顺序排列,得1,3,3,3,4,6,6,8,8,8,则这组数据的中位数为=5,故A正确;
平均数为=5,故C正确;
则方差为×[(1-5)2+(4-5)2+(3-5)2×3+(8-5)2×3+(6-5)2×2]=5.8,故B错误;
因为10×85%=8.5,所以85%分位数是从小到大第9个数字,为8,故D正确,故选ACD.
15.BD 解析 因为a=(2,1),b=(-6,2),c=,-,
所以a·b=-12+2=-10≠-6,故A错误;
向量a在向量b上的投影向量为=-b=-b,故B正确;
因为a+b=(-4,3),a-b=(8,-1),
所以(a+b)·(a-b)=-32-3=-35≠0,故C错误;
因为a·c=2×=0,所以a⊥c,故D正确.故选BD.
16.AD 解析 因为f(x)=sin2x++2cos(2x+φ)且f(0)=f,所以sin+2cos φ=sin+2cos+φ,即2cos φ=2coscos φ-2sinsin φ,所以tan φ=-,
因为-≤φ≤,所以φ=-,
所以f(x)=sin2x++2cos2x-=sin2x++2cos2x+-=3sin2x+,
因为f=3sin2×=3sin=3,
所以f(x)的图象的一条对称轴方程为x=,故A正确;
当x∈0,时,2x+∈,所以sin2x+∈-,1,则f(x)∈-,3,故B错误;
将g(x)=3sin 2x的图象向左平移个单位长度得到y=3sin 2x+=3sin2x+的图象,故C错误;
因为f-=3sin-2×=3sin 0=0,所以f(x)的图象的一个对称中心为-,0,故D正确.故选AD.
17. 解析 ∵cos B=,B为三角形内角,
∴sin B=,
∴sin C=sin[π-(A+B)]=sin(A+B)=sincos B+cossin B=.
由正弦定理可得,即AC=.
18.(-∞,4] 解析 当-1
若a<0,则f(x)=x+-4单调递增,所以f(x)在(0,+∞)内的取值范围为R,所以a<0满足题意;
若a>0,则当x>时,f(x)单调递增,当0
19. 14 解析 +,所以·=×36=14.
20. 解析 过点M作MH垂直AB于点H,连接NH,如图所示,因为平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,MH在平面ABCD内,MH⊥AB,则MH⊥平面ABEF,NH 平面ABEF,所以MH⊥NH.
由已知弹珠N的速度是弹珠M的速度的3倍,设AM=a,则NF=3a0≤a≤,因为四边形ABCD,ABEF为正方形,AB=2,则AC=BF=2,∠ABF=∠CAB=45°,所以MH=AH=a,所以BH=2-a,BN=2-3a,在△BHN中,由余弦定理可得|NH|2=|BH|2+|BN|2-2|BH|·|BN|cos 45°=2-a2+(2-3a)2-22-a(2-3a)·=4-2a+a2+8-12a+9a2-(2-a)(2-3a)=4-6a+a2,
所以|MN|2=|MH|2+|NH|2=7a2-6a+40≤a≤,
当a=时,|MN,所以|MN|min=.
21.解 (1)甲小组研发芯片A成功的概率为p1=,乙小组研发芯片B成功的概率为p2=,由于两个小组的研发相互独立,所以A,B两种芯片研发都成功的概率P1=p1·p2=.
(2)该公司获得政府奖励则需有芯片研发成功,根据对立事件可知获奖的概率为P2=1-(1-p1)(1-p2)=1-1-×1-=1-.
22.解 (1)在题图1中,连接AC交DE于点F,易知AC=2.
因为,∠DAE=∠ABC=90°,所以△DAE∽△ABC,可得AC⊥DE.
易知△DFC∽△EFA,则AF=,CF=,因为平面A1DE⊥平面EBCD,平面A1DE∩平面EBCD=DE,A1F 平面A1DE,所以A1F⊥平面EBCD.
则∠A1CF是直线A1C与平面EBCD所成角,tan∠A1CF=.
(2)如图,作出A1F,AC,过点A1作A1H⊥FC,垂足为H,过点H作HG⊥DC,垂足为G,连接A1G.
由(1)可知DE⊥CF,DE⊥A1F,CF∩A1F=F,CF,A1F 平面A1FC,则DE⊥平面A1FC,且A1H 平面A1FC,可得A1H⊥DE.
且A1H⊥FC,FC∩DE=F,DE,FC 平面BCDE,所以A1H⊥平面BCDE.
由CD 平面BCDE,可得A1H⊥CD.
又因为HG⊥CD,A1H∩HG=H,A1H,HG 平面A1HG,所以CD⊥平面A1HG,由A1G 平面A1HG,可得CD⊥A1G,所以∠A1GH是二面角A1-CD-B的平面角,设∠A1FC=θ,θ∈(0,π),由(1)可知A1F=,FC=,
在Rt△A1FH中,A1H=sin θ,FH=cos θ,则CH=FC-FH=(2-cos θ),
因为HG⊥DC,则HG∥AD,可得,所以HG=(2-cos θ),
在Rt△A1HG中,tan∠A1GH=.
设y=,θ∈(0,π),则y>0,sin θ+ycos θ=sin(θ+φ)=2y,其中sin φ=,cos φ=,即sin(θ+φ)=≤1,解得0
23.解 (1)当a=0时,f(x)=x|x|+x,f(-x)=-x|-x|-x=-f(x),所以函数f(x)为奇函数.
(2)f(x)=
函数y=x2+(1-a)x的图象的对称轴为直线x=,函数y=-x2+(a+1)x的图象的对称轴为直线x=.
若函数f(x)在R上是增函数,则≤a≤,解得-1≤a≤1,即a的取值范围是[-1,1].
(3)方程f(x)-tf(a)=0的解即为方程f(x)=tf(a)的解.
①当-1≤a≤1时,函数f(x)在R上是增函数,所以关于x的方程f(x)=tf(a)不可能有三个不相等的实数根;
②当a>1时,即a>,所以函数f(x)在-∞,内单调递增,在,a内单调递减,在(a,+∞)内单调递增,当f(a)
因为存在a∈[-2,3]使得关于x的方程f(x)=tf(a)有三个不相等的实数根,
所以1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
