2024普通高中学业水平考试数学模拟卷2(含解析)
文档属性
| 名称 | 2024普通高中学业水平考试数学模拟卷2(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 449.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:25:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024普通高中学业水平考试数学模拟卷(二)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知集合A={-1,0,1},集合B={x∈N|x2=1},那A∩B=( )
A.{1} B.{0,1} C.{-1,1} D.{-1,0,1}
2.设z=,则z的共轭复数的虚部为( )
A. B.i C.- D.-i
3.在下列函数中,定义域为(0,+∞)的是( )
A.f(x)=ex B.f(x)=ln x C.f(x)= D.f(x)=|x|
4.“θ=”是“cos θ=”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
5.如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是( )
A. B. C. D.1
6.已知向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c,则λ=( )
A. B. C.1 D.2
7.已知球O的体积为36π,则该球的表面积为( )
A.6π B.9π C.12π D.36π
8.已知3a+27b=6,则a+3b的最大值是( )
A.2 B.6 C.2 D.2
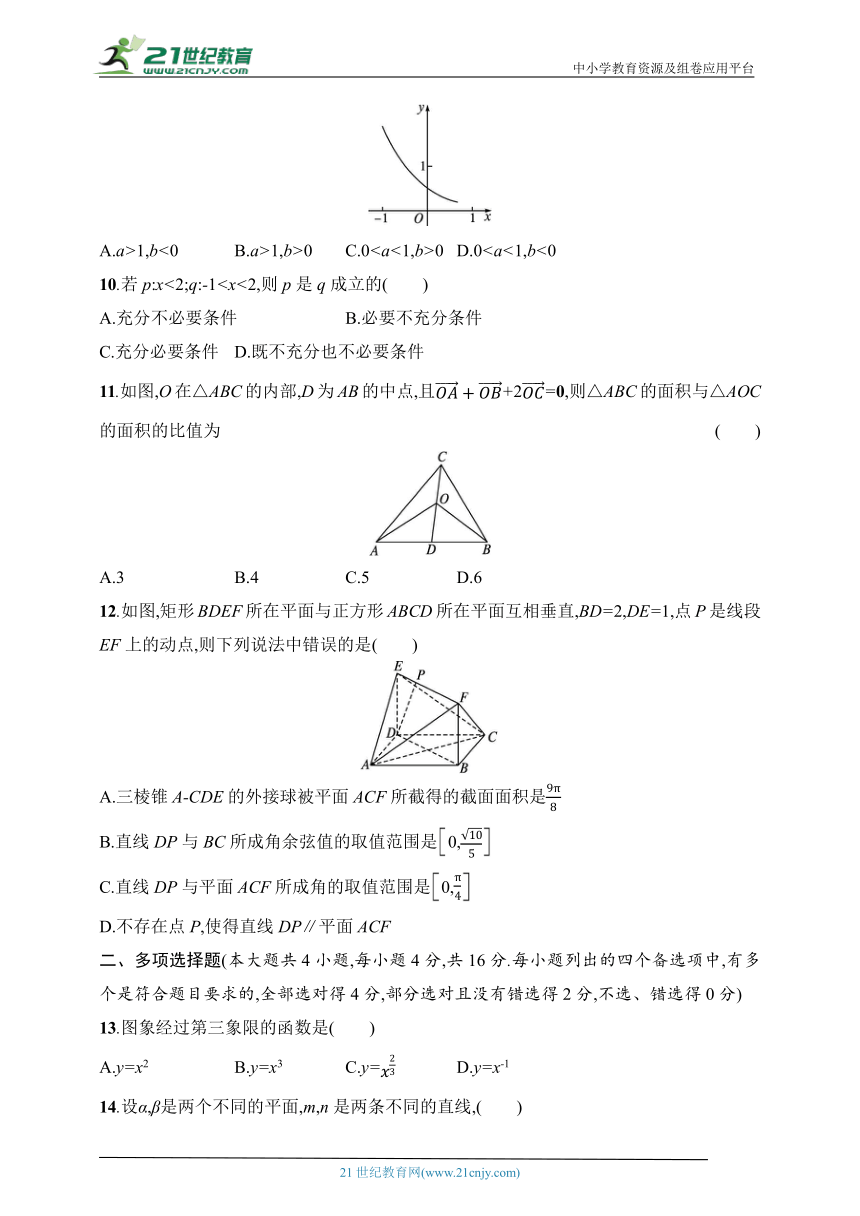
9.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0 C.00 D.010.若p:x<2;q:-1A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
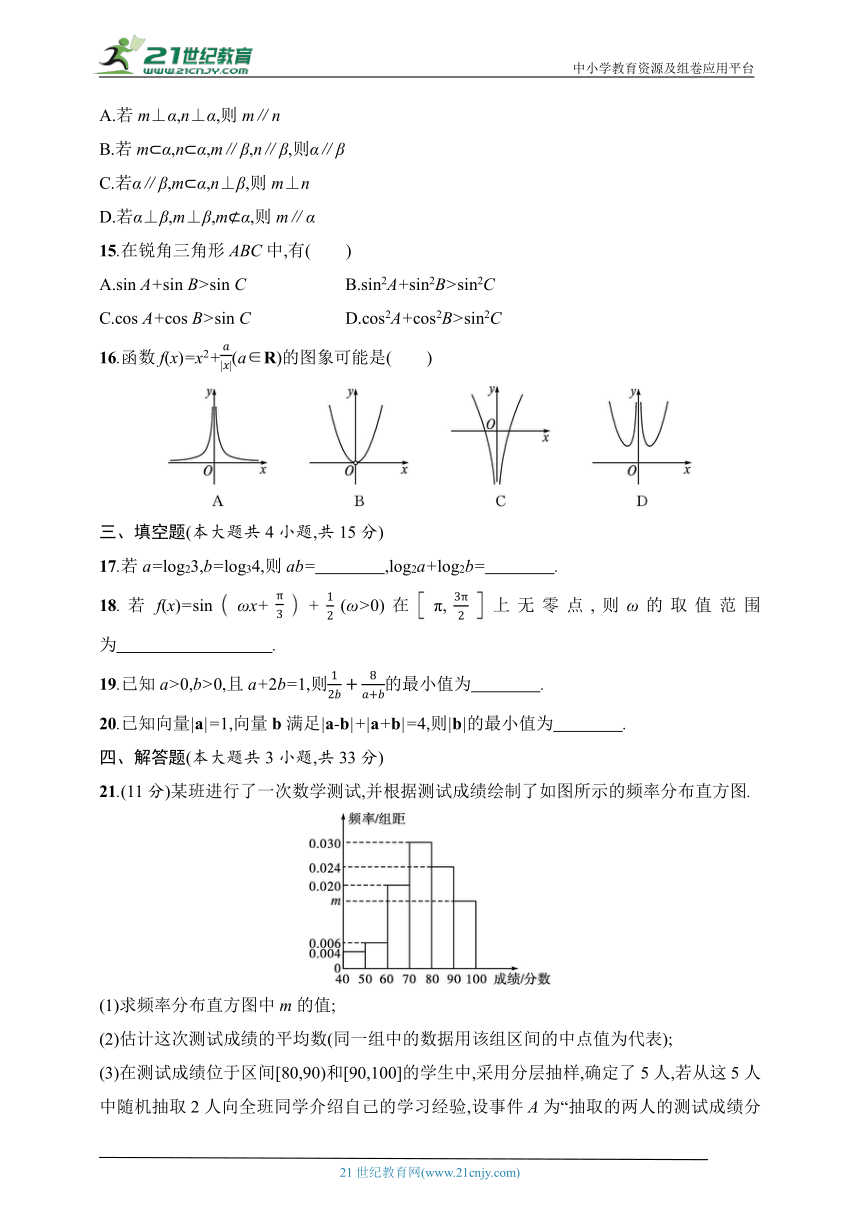
11.如图,O在△ABC的内部,D为AB的中点,且+2=0,则△ABC的面积与△AOC的面积的比值为 ( )
A.3 B.4 C.5 D.6
12.如图,矩形BDEF所在平面与正方形ABCD所在平面互相垂直,BD=2,DE=1,点P是线段EF上的动点,则下列说法中错误的是( )
A.三棱锥A-CDE的外接球被平面ACF所截得的截面面积是
B.直线DP与BC所成角余弦值的取值范围是0,
C.直线DP与平面ACF所成角的取值范围是0,
D.不存在点P,使得直线DP∥平面ACF
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.图象经过第三象限的函数是( )
A.y=x2 B.y=x3 C.y= D.y=x-1
14.设α,β是两个不同的平面,m,n是两条不同的直线,( )
A.若m⊥α,n⊥α,则m∥n
B.若m α,n α,m∥β,n∥β,则α∥β
C.若α∥β,m α,n⊥β,则m⊥n
D.若α⊥β,m⊥β,m α,则m∥α
15.在锐角三角形ABC中,有( )
A.sin A+sin B>sin C B.sin2A+sin2B>sin2C
C.cos A+cos B>sin C D.cos2A+cos2B>sin2C
16.函数f(x)=x2+(a∈R)的图象可能是( )
三、填空题(本大题共4小题,共15分)
17.若a=log23,b=log34,则ab= ,log2a+log2b= .
18.若f(x)=sinωx++(ω>0)在π,上无零点,则ω的取值范围为 .
19.已知a>0,b>0,且a+2b=1,则的最小值为 .
20.已知向量|a|=1,向量b满足|a-b|+|a+b|=4,则|b|的最小值为 .
四、解答题(本大题共3小题,共33分)
21.(11分)某班进行了一次数学测试,并根据测试成绩绘制了如图所示的频率分布直方图.
(1)求频率分布直方图中m的值;
(2)估计这次测试成绩的平均数(同一组中的数据用该组区间的中点值为代表);
(3)在测试成绩位于区间[80,90)和[90,100]的学生中,采用分层抽样,确定了5人,若从这5人中随机抽取2人向全班同学介绍自己的学习经验,设事件A为“抽取的两人的测试成绩分别位于[80,90)和[90,100]”,求事件A的概率P(A).
22.(11分)如图,在三棱柱ABC-A1B1C1中,点A1在平面ABC内的投影D在线段AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面ABC所成角为60°,求二面角A1-AB-C的平面角的余弦值.
23.(11分)已知函数f(x)=-,其中a为常数,且a>1.
(1)若f(x)是奇函数,求a的值;
(2)证明:f(x)在(0,+∞)内有唯一的零点;
(3)设f(x)在(0,+∞)内的零点为x0,证明:x0-1>loga2-.
普通高中学业水平考试数学模拟卷(二)
1.A 解析 由于B={x∈N|x2=1}={1},所以A∩B={1}.故选A.
2.C 解析 因为z=i,所以i,所以的虚部为-,故选C.
3.B 解析 对于A选项,函数f(x)=ex的定义域为R;
对于B选项,函数f(x)=ln x的定义域为(0,+∞);
对于C选项,函数f(x)=的定义域为{x|x≠0};
对于D选项,函数f(x)=|x|的定义域为R.故选B.
4.A 解析 当θ=时,cos θ=cos,
而当cos θ=时,θ=+2kπ或θ=-+2kπ,k∈Z,
所以“θ=”是“cos θ=”的充分不必要条件,故选A.
5.B 解析 根据题意,闭合两个开关所有的可能为(S1,S2),(S1,S3),(S2,S3),其中能形成闭合电路的为(S1,S2),(S1,S3),所以同时闭合两个开关能形成闭合电路的概率为.故选B.
6.B 解析 因为向量a=(1,2),b=(1,0),所以a+λb=(1,2)+λ(1,0)=(1+λ,2),因为(a+λb)∥c,c=(3,4),所以,解得λ=,故选B.
7.D 解析 设球的体积为R,则由题可得πR3=36π,解得R=3,则该球的表面积为4π×32=36π.故选D.
8.C 解析 由3a+27b=6有3a+27b=3a+33b≥2=2,当且仅当a=3b=1时,等号成立.所以6≥2,即36≥4×3a+3b,所以9≥3a+3b,所以a+3b≤2,故选C.
9. D 解析 由函数f(x)=ax-b的图象可知,函数f(x)=ax-b在定义域上单调递减,∴0函数f(x)=ax-b图象是由y=ax向左平移所得,
∴-b>0,∴b<0.故D选项正确.故选D.
10.B 解析 由x<2不能推出-111.B 解析 ∵D为AB的中点,∴=2,
∵+2=0,∴=-,∴O是CD的中点,
∴S△AOC=S△AOD=S△AOB=S△ABC,故选B.
12.D 解析 在△ACF中,AF=CF=,显然有FO⊥AC,sin∠FAC=,由正弦定理得△ACF外接圆直径2R=,R=,
以DA,DC,DE为长、宽、高作长方体,如图,则三棱锥A-CDE的外接球即为长方体的外接球,三棱锥A-CDE的外接球被平面ACF所截得的截面是△ACF的外接圆,其面积为πR2=,故A正确.
因为平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,ED⊥BD,ED 平面BDEF,所以ED⊥平面ABCD,因为BF∥ED,所以BF⊥平面ABCD.
因为AD,AB,BC,BD 平面ABCD,所以ED⊥AD,ED⊥BD,BF⊥AB,BF⊥BC,
因为BD=2,DE=1,所以AD=,EA=,DF=,AF=CF=,
又因为BC∥AD,所以直线DP与BC所成角为∠ADP(或其补角),
因为·()=·(+λ)=λ=2λcos 45°=2λ(0≤λ≤1),
而||2=(+λ)2=1+4λ2,||=,
所以||=,
当λ=0时,cos∠ADP==0,
当0<λ≤1时,cos∠ADP=,
综上,0≤cos∠ADP≤,故B正确;
设点D到平面ACF的距离为d,因为AF=FC=,AC=BD=2,所以S△AFC=AC·OF=×2×,又因为S△ABC=AB·BC==1,
由VB-AFC=VF-ABC=dS△AFC=FB·S△ABC,
即d=1,解得d=,设直线DP与平面ACF所成角为θ,
取EF中点G,连接DG,令AC∩BD=O,连接FO,如图,当点P与点G重合时,直线DP∥平面ACF,直线DP与平面ACF所成角θ=0,
当点P由点G向点E,F运动时,θ变大,当运动到点E时,因为DE∥BF,
所以sin θ=,由0≤θ≤知,θ=,
当运动到点F时,sin θ=,
综上知,θ∈0,,故C正确;
在正方形ABCD中,O为BD中点,而四边形BDEF是矩形,则DO∥GF且DO=GF,即四边形DGFO是平行四边形,即有DG∥FO,而FO 平面ACF,DG 平面ACF,于是得DG∥平面ACF,当点P与点 G重合时,直线DP∥平面ACF,故D错误;故选D.
13.BD 解析 由幂函数的图象可知,
在选项A中,y=x2过第一、二象限;
在选项B中,y=x3过第一、三象限;
在选项C中,y=≥0且定义域为R,过第一、二象限;
在选项D中,y=x-1过第一、三象限.故选BD.
14.ACD 解析 对选项A,垂直于同一平面的两条直线平行,正确;
对选项B,当m∥n时结论未必成立,错误;
对选项C,α∥β,n⊥β,故n⊥α,又m α,故m⊥n,正确;
对选项D,α⊥β,m⊥β,则m∥α或m α,排除m α,则m∥α,正确.故选ACD.
15.ABC 解析 对于A,根据正弦定理,因为a+b>c可得sin A+sin B>sin C,故A正确;
对于B,因为cos C=>0可得a2+b2>c2,再由正弦定理可得sin2A+sin2B>sin2C,故B正确;
对于C,因为0cos Asin B+cos Bsin A=sin(A+B)=sin C,故C正确;
对于D,当A=B=C= cos2A+cos2B==sin2C,故D错误.故选ABC.
16.BCD 解析 ∵f(-x)=(-x)2+=x2+=f(x),
∴f(x)为偶函数,
当a=0时,f(x)=x2(x≠0),此时图象与B相符;
当a<0时,若x>0,则f(x)=x2+,此时f(x)单调递增,由偶函数性质可知,f(x)在(-∞,0)内单调递减,图象与C相符;
当a=1时,f(x)=x2+,函数图象类似D,当x→+∞时,f(x)→+∞.
故图象不可能为A.故选BCD.
17.2 1 解析 由换底公式得a=log23=,b=,所以ab==2,log2a+log2b=log2(ab)=log22=1.
18.0,∪,1∪ 解析 因为函数f(x)=sinωx++(ω>0)在π,上无零点,所以-π,所以0<ω<2;
由f(x)=sinωx++=0,得sinωx+=-,所以ωx++2kπ(k∈Z)或ωx++2kπ(k∈Z),
由ωx+,得x=;
由ωx+,得x=;
由ωx+,得x=,因为函数f(x)=sinωx++(ω>0)在π,上无零点,所以又因为ω>0,所以ω的取值范围为0,∪,1∪.
19. 解析 ==17+≥17+2=,
当且仅当,a=3,b=时,等号成立,
即的最小值为.
20. 解析 由平行四边形性质可得|a+b|2+|a-b|2=2(|a|2+|b|2),
由基本不等式可得|a+b|2+|a-b|2≥,当且仅当|a+b|=|a-b|时,等号成立,所以2(|a|2+|b|2)≥,即2(1+|b|2)≥,所以|b|≥,所以|b|的最小值为.
21.解 (1)由频率分布直方图的性质,可得(0.004+0.006+0.020+0.030+0.024+m)×10=1,解得m=0.016.
(2)根据频率分布直方图的平均数的计算公式,这次测试成绩的平均数为=(0.004×45+0.006×55+0.020×65+0.030×75+0.024×85+0.016×95)×10=76.2(分).
(3)测试成绩位于[80,90)的频率P1=0.024×10=0.24,位于[90,100]的频率P2=0.016×10=0.16,因为P1∶P2=3∶2,所以确定的5人中成绩在[80,90)内的有3人,分别记为A1,A2,A2,成绩在[90,100]上的有2人,分别记为B1,B2,从5人中随机抽取2人的样本空间Ω={(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)},共有10个样本点,
其中A={(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2)},即n(A)=6,所以概率为P(A)=.
22.(1)证明 因为A1D⊥平面ABC,A1D 平面A1AC,
所以平面ACC1A1⊥平面ABC且交于AC,
又因为BC⊥AC,所以BC⊥平面ACC1A1,因此BC⊥AC1,在平行四边形ACC1A1中,AC=CC1=2,所以四边形ACC1A1为菱形,故A1C⊥AC1,又因为A1C∩BC=C,所以AC1⊥平面CBA1,而A1B 平面CBA1,因此AC1⊥A1B.
(2)解 因为A1D⊥平面ABC,所以∠A1AD即为直线AA1与平面ABC所成的角,故∠A1AD=60°,作DK⊥AB于点K,连接A1K(图略),则A1K⊥AB,所以∠A1KD即为二面角A1-AB-C的平面角,在Rt△A1AD中,A1D=A1Asin 60°=,在Rt△AKD中,DK=ADsin∠CAB=,在Rt△A1KD中,tan∠A1KD=A1D=,所以cos∠A1KD=,即二面角A1-AB-C的平面角的余弦值为.
23.(1)解 由题意, x≠0,f(-x)=-f(x)恒成立,即-=--,化简得1=,解得a=2.
(2)证明 由题意,f(x)=-,
∵a>1,∴f(x)在(0,+∞)内是增函数,又f(1)=-<0,f(2)=->0,
∴由零点存在定理可知f(x)在(0,+∞)内有唯一的零点.
(3)证明 由f(x0)=0可知-=0,即+1==a1+,
由(2)可知1a1+=2a,
∴>2a-1,即x0>loga(2a-1),
∴x0-1>loga2-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024普通高中学业水平考试数学模拟卷(二)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知集合A={-1,0,1},集合B={x∈N|x2=1},那A∩B=( )
A.{1} B.{0,1} C.{-1,1} D.{-1,0,1}
2.设z=,则z的共轭复数的虚部为( )
A. B.i C.- D.-i
3.在下列函数中,定义域为(0,+∞)的是( )
A.f(x)=ex B.f(x)=ln x C.f(x)= D.f(x)=|x|
4.“θ=”是“cos θ=”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
5.如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是( )
A. B. C. D.1
6.已知向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c,则λ=( )
A. B. C.1 D.2
7.已知球O的体积为36π,则该球的表面积为( )
A.6π B.9π C.12π D.36π
8.已知3a+27b=6,则a+3b的最大值是( )
A.2 B.6 C.2 D.2
9.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0 C.0
C.充分必要条件 D.既不充分也不必要条件
11.如图,O在△ABC的内部,D为AB的中点,且+2=0,则△ABC的面积与△AOC的面积的比值为 ( )
A.3 B.4 C.5 D.6
12.如图,矩形BDEF所在平面与正方形ABCD所在平面互相垂直,BD=2,DE=1,点P是线段EF上的动点,则下列说法中错误的是( )
A.三棱锥A-CDE的外接球被平面ACF所截得的截面面积是
B.直线DP与BC所成角余弦值的取值范围是0,
C.直线DP与平面ACF所成角的取值范围是0,
D.不存在点P,使得直线DP∥平面ACF
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.图象经过第三象限的函数是( )
A.y=x2 B.y=x3 C.y= D.y=x-1
14.设α,β是两个不同的平面,m,n是两条不同的直线,( )
A.若m⊥α,n⊥α,则m∥n
B.若m α,n α,m∥β,n∥β,则α∥β
C.若α∥β,m α,n⊥β,则m⊥n
D.若α⊥β,m⊥β,m α,则m∥α
15.在锐角三角形ABC中,有( )
A.sin A+sin B>sin C B.sin2A+sin2B>sin2C
C.cos A+cos B>sin C D.cos2A+cos2B>sin2C
16.函数f(x)=x2+(a∈R)的图象可能是( )
三、填空题(本大题共4小题,共15分)
17.若a=log23,b=log34,则ab= ,log2a+log2b= .
18.若f(x)=sinωx++(ω>0)在π,上无零点,则ω的取值范围为 .
19.已知a>0,b>0,且a+2b=1,则的最小值为 .
20.已知向量|a|=1,向量b满足|a-b|+|a+b|=4,则|b|的最小值为 .
四、解答题(本大题共3小题,共33分)
21.(11分)某班进行了一次数学测试,并根据测试成绩绘制了如图所示的频率分布直方图.
(1)求频率分布直方图中m的值;
(2)估计这次测试成绩的平均数(同一组中的数据用该组区间的中点值为代表);
(3)在测试成绩位于区间[80,90)和[90,100]的学生中,采用分层抽样,确定了5人,若从这5人中随机抽取2人向全班同学介绍自己的学习经验,设事件A为“抽取的两人的测试成绩分别位于[80,90)和[90,100]”,求事件A的概率P(A).
22.(11分)如图,在三棱柱ABC-A1B1C1中,点A1在平面ABC内的投影D在线段AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面ABC所成角为60°,求二面角A1-AB-C的平面角的余弦值.
23.(11分)已知函数f(x)=-,其中a为常数,且a>1.
(1)若f(x)是奇函数,求a的值;
(2)证明:f(x)在(0,+∞)内有唯一的零点;
(3)设f(x)在(0,+∞)内的零点为x0,证明:x0-1>loga2-.
普通高中学业水平考试数学模拟卷(二)
1.A 解析 由于B={x∈N|x2=1}={1},所以A∩B={1}.故选A.
2.C 解析 因为z=i,所以i,所以的虚部为-,故选C.
3.B 解析 对于A选项,函数f(x)=ex的定义域为R;
对于B选项,函数f(x)=ln x的定义域为(0,+∞);
对于C选项,函数f(x)=的定义域为{x|x≠0};
对于D选项,函数f(x)=|x|的定义域为R.故选B.
4.A 解析 当θ=时,cos θ=cos,
而当cos θ=时,θ=+2kπ或θ=-+2kπ,k∈Z,
所以“θ=”是“cos θ=”的充分不必要条件,故选A.
5.B 解析 根据题意,闭合两个开关所有的可能为(S1,S2),(S1,S3),(S2,S3),其中能形成闭合电路的为(S1,S2),(S1,S3),所以同时闭合两个开关能形成闭合电路的概率为.故选B.
6.B 解析 因为向量a=(1,2),b=(1,0),所以a+λb=(1,2)+λ(1,0)=(1+λ,2),因为(a+λb)∥c,c=(3,4),所以,解得λ=,故选B.
7.D 解析 设球的体积为R,则由题可得πR3=36π,解得R=3,则该球的表面积为4π×32=36π.故选D.
8.C 解析 由3a+27b=6有3a+27b=3a+33b≥2=2,当且仅当a=3b=1时,等号成立.所以6≥2,即36≥4×3a+3b,所以9≥3a+3b,所以a+3b≤2,故选C.
9. D 解析 由函数f(x)=ax-b的图象可知,函数f(x)=ax-b在定义域上单调递减,∴0
∴-b>0,∴b<0.故D选项正确.故选D.
10.B 解析 由x<2不能推出-1
∵+2=0,∴=-,∴O是CD的中点,
∴S△AOC=S△AOD=S△AOB=S△ABC,故选B.
12.D 解析 在△ACF中,AF=CF=,显然有FO⊥AC,sin∠FAC=,由正弦定理得△ACF外接圆直径2R=,R=,
以DA,DC,DE为长、宽、高作长方体,如图,则三棱锥A-CDE的外接球即为长方体的外接球,三棱锥A-CDE的外接球被平面ACF所截得的截面是△ACF的外接圆,其面积为πR2=,故A正确.
因为平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,ED⊥BD,ED 平面BDEF,所以ED⊥平面ABCD,因为BF∥ED,所以BF⊥平面ABCD.
因为AD,AB,BC,BD 平面ABCD,所以ED⊥AD,ED⊥BD,BF⊥AB,BF⊥BC,
因为BD=2,DE=1,所以AD=,EA=,DF=,AF=CF=,
又因为BC∥AD,所以直线DP与BC所成角为∠ADP(或其补角),
因为·()=·(+λ)=λ=2λcos 45°=2λ(0≤λ≤1),
而||2=(+λ)2=1+4λ2,||=,
所以||=,
当λ=0时,cos∠ADP==0,
当0<λ≤1时,cos∠ADP=,
综上,0≤cos∠ADP≤,故B正确;
设点D到平面ACF的距离为d,因为AF=FC=,AC=BD=2,所以S△AFC=AC·OF=×2×,又因为S△ABC=AB·BC==1,
由VB-AFC=VF-ABC=dS△AFC=FB·S△ABC,
即d=1,解得d=,设直线DP与平面ACF所成角为θ,
取EF中点G,连接DG,令AC∩BD=O,连接FO,如图,当点P与点G重合时,直线DP∥平面ACF,直线DP与平面ACF所成角θ=0,
当点P由点G向点E,F运动时,θ变大,当运动到点E时,因为DE∥BF,
所以sin θ=,由0≤θ≤知,θ=,
当运动到点F时,sin θ=,
综上知,θ∈0,,故C正确;
在正方形ABCD中,O为BD中点,而四边形BDEF是矩形,则DO∥GF且DO=GF,即四边形DGFO是平行四边形,即有DG∥FO,而FO 平面ACF,DG 平面ACF,于是得DG∥平面ACF,当点P与点 G重合时,直线DP∥平面ACF,故D错误;故选D.
13.BD 解析 由幂函数的图象可知,
在选项A中,y=x2过第一、二象限;
在选项B中,y=x3过第一、三象限;
在选项C中,y=≥0且定义域为R,过第一、二象限;
在选项D中,y=x-1过第一、三象限.故选BD.
14.ACD 解析 对选项A,垂直于同一平面的两条直线平行,正确;
对选项B,当m∥n时结论未必成立,错误;
对选项C,α∥β,n⊥β,故n⊥α,又m α,故m⊥n,正确;
对选项D,α⊥β,m⊥β,则m∥α或m α,排除m α,则m∥α,正确.故选ACD.
15.ABC 解析 对于A,根据正弦定理,因为a+b>c可得sin A+sin B>sin C,故A正确;
对于B,因为cos C=>0可得a2+b2>c2,再由正弦定理可得sin2A+sin2B>sin2C,故B正确;
对于C,因为0
对于D,当A=B=C= cos2A+cos2B==sin2C,故D错误.故选ABC.
16.BCD 解析 ∵f(-x)=(-x)2+=x2+=f(x),
∴f(x)为偶函数,
当a=0时,f(x)=x2(x≠0),此时图象与B相符;
当a<0时,若x>0,则f(x)=x2+,此时f(x)单调递增,由偶函数性质可知,f(x)在(-∞,0)内单调递减,图象与C相符;
当a=1时,f(x)=x2+,函数图象类似D,当x→+∞时,f(x)→+∞.
故图象不可能为A.故选BCD.
17.2 1 解析 由换底公式得a=log23=,b=,所以ab==2,log2a+log2b=log2(ab)=log22=1.
18.0,∪,1∪ 解析 因为函数f(x)=sinωx++(ω>0)在π,上无零点,所以-π,所以0<ω<2;
由f(x)=sinωx++=0,得sinωx+=-,所以ωx++2kπ(k∈Z)或ωx++2kπ(k∈Z),
由ωx+,得x=;
由ωx+,得x=;
由ωx+,得x=,因为函数f(x)=sinωx++(ω>0)在π,上无零点,所以又因为ω>0,所以ω的取值范围为0,∪,1∪.
19. 解析 ==17+≥17+2=,
当且仅当,a=3,b=时,等号成立,
即的最小值为.
20. 解析 由平行四边形性质可得|a+b|2+|a-b|2=2(|a|2+|b|2),
由基本不等式可得|a+b|2+|a-b|2≥,当且仅当|a+b|=|a-b|时,等号成立,所以2(|a|2+|b|2)≥,即2(1+|b|2)≥,所以|b|≥,所以|b|的最小值为.
21.解 (1)由频率分布直方图的性质,可得(0.004+0.006+0.020+0.030+0.024+m)×10=1,解得m=0.016.
(2)根据频率分布直方图的平均数的计算公式,这次测试成绩的平均数为=(0.004×45+0.006×55+0.020×65+0.030×75+0.024×85+0.016×95)×10=76.2(分).
(3)测试成绩位于[80,90)的频率P1=0.024×10=0.24,位于[90,100]的频率P2=0.016×10=0.16,因为P1∶P2=3∶2,所以确定的5人中成绩在[80,90)内的有3人,分别记为A1,A2,A2,成绩在[90,100]上的有2人,分别记为B1,B2,从5人中随机抽取2人的样本空间Ω={(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)},共有10个样本点,
其中A={(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2)},即n(A)=6,所以概率为P(A)=.
22.(1)证明 因为A1D⊥平面ABC,A1D 平面A1AC,
所以平面ACC1A1⊥平面ABC且交于AC,
又因为BC⊥AC,所以BC⊥平面ACC1A1,因此BC⊥AC1,在平行四边形ACC1A1中,AC=CC1=2,所以四边形ACC1A1为菱形,故A1C⊥AC1,又因为A1C∩BC=C,所以AC1⊥平面CBA1,而A1B 平面CBA1,因此AC1⊥A1B.
(2)解 因为A1D⊥平面ABC,所以∠A1AD即为直线AA1与平面ABC所成的角,故∠A1AD=60°,作DK⊥AB于点K,连接A1K(图略),则A1K⊥AB,所以∠A1KD即为二面角A1-AB-C的平面角,在Rt△A1AD中,A1D=A1Asin 60°=,在Rt△AKD中,DK=ADsin∠CAB=,在Rt△A1KD中,tan∠A1KD=A1D=,所以cos∠A1KD=,即二面角A1-AB-C的平面角的余弦值为.
23.(1)解 由题意, x≠0,f(-x)=-f(x)恒成立,即-=--,化简得1=,解得a=2.
(2)证明 由题意,f(x)=-,
∵a>1,∴f(x)在(0,+∞)内是增函数,又f(1)=-<0,f(2)=->0,
∴由零点存在定理可知f(x)在(0,+∞)内有唯一的零点.
(3)证明 由f(x0)=0可知-=0,即+1==a1+,
由(2)可知1
∴>2a-1,即x0>loga(2a-1),
∴x0-1>loga2-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
