2024普通高中学业水平考试数学模拟卷4(含解析)
文档属性
| 名称 | 2024普通高中学业水平考试数学模拟卷4(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 390.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024普通高中学业水平考试数学模拟卷(四)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知集合A={1,2,3},B={2,4},则A∪B=( )
A.{2} B.{2,3,4} C.{1,2,3,4} D.{0,2,3,4}
2.已知i为虚数单位,则复数(1+2i)+(-3+2i)在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.函数f(x)=+lg(x-1)的定义域为( )
A.{x|x≥2} B.{x|x<1} C.{x|1≤x≤2} D.{x|14.已知a=(2,1),b=(x,-2),若a∥b,则a+b=( )
A.(-2,-1) B.(2,1) C.(3,-1) D.(-3,1)
5.已知α∈π,,且tan α=,则cos α=( )
A.- B. C.- D.
6.“a≤1”是“方程x2+2x+a=0(a∈R)有正实数根”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知圆锥的底面半径为1,其侧面展开图是半圆,则该圆锥的体积为( )
A. B.π C. D.2π
8.已知a=,b=ln,c=sin,则( )
A.a>b>c B.b>c>a C.c>a>b D.a>c>b
9.现测得某放射性元素的半衰期为1 350年(每经过1 350年,该元素的存量为原来的一半),某生物标本中该放射性元素的初始存量为m,经检测现在的存量为.据此推测该生物距今约为( )(参考数据:lg 2≈0.3)
A.2 452年 B.2 750年 C.3 150年 D.3 856年
10.已知函数f(x)=lg(x+)-,则不等式f(2x+1)+f(x)>-2的解集为( )
A.-,+∞ B.-,100 C.-∞,- D.-,100
11.已知正实数x,y满足x+2y=1,则的最小值为( )
A. B. C. D.
12.在四面体ABCD中,△ABC与△BCD都是边长为6的等边三角形,且二面角A-BC-D的大小为60°,则四面体ABCD外接球的表面积是( )
A.52π B.54π
C.56π D.60π
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.已知a,b∈R,则下列选项中能使成立的是( )
A.b>a>0 B.a>b>0
C.b<014.不透明的袋中装有5个大小质地完全相同的小球,其中3个红球、2个白球,从袋中一次性取出2个球,记事件A=“两球同色”,事件B=“两球异色”,事件C=“至少有一红球”,则( )
A.P(A)= B.P(C)=
C.事件A与事件B是对立事件 D.事件A与事件B是相互独立事件
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,则( )
A.若A>B,则sin 2A>sin 2B
B.若S△ABC=1,a=1,则sin A的最大值为
C.若a=2,b=4,A=,则满足条件的三角形有两个
D.若·=0,且,则△ABC为等边三角形
16.已知定义在R上的函数y=f(x)满足fx-=-f(x),且fx+为奇函数,f(-1)=-1,f(0)=2.下列说法正确的是( )
A.3是函数y=f(x)的一个周期
B.函数y=f(x)的图象关于直线x=对称
C.函数y=f(x)是偶函数
D.f(1)+f(2)+f(3)+…+f(2 023)=2
三、填空题(本大题共4小题,共15分)
17.已知f(x)是幂函数,且满足:①f(-x)=f(x);②f(x)在(0,+∞)内单调递增,请写出符合上述条件的一个函数f(x)= .
18.已知a=(2,1),b为单位向量,且(a+2b)⊥(a-b),则a·b= ,向量b在向量a上的投影向量为 .
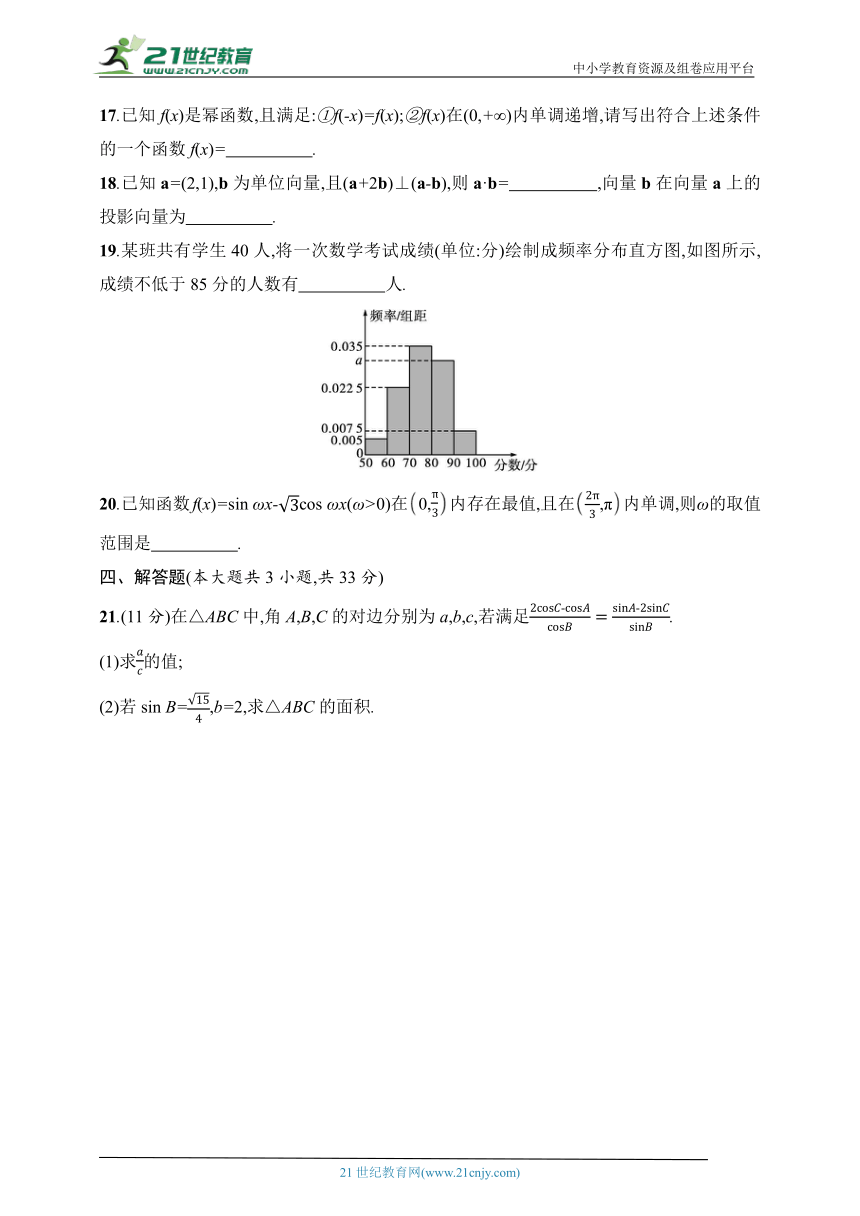
19.某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示,成绩不低于85分的人数有 人.
20.已知函数f(x)=sin ωx-cos ωx(ω>0)在0,内存在最值,且在,π内单调,则ω的取值范围是 .
四、解答题(本大题共3小题,共33分)
21.(11分)在△ABC中,角A,B,C的对边分别为a,b,c,若满足.
(1)求的值;
(2)若sin B=,b=2,求△ABC的面积.
22.(11分) 已知四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AB=AD=2BC=2,E为PD的中点.
(1)求证:CE∥平面PAB;
(2)设平面EAC与平面DAC的夹角为45°,求三棱锥E-ACD的体积.
23.(11分)已知函数f(x)=log2[(3m-6)x+2m-5],g(x)=log2+m,m∈R.
(1)若f(1)=2,求m的值;
(2)若方程g(x)-f(x)=0恰有一个实根,求m的取值范围;
(3)设m>0,若对任意t∈,2,当x1,x2∈[t,t+1]时,满足|g(x1)-g(x2)|≤1,求m的取值范围.
普通高中学业水平考试数学模拟卷(四)
1.C
2.B 解析 因为(1+2i)+(-3+2i)=-2+4i,所以该复数在复平面内对应的点的坐标为(-2,4),位于第二象限.故选B.
3.D 解析 由题意,要使f(x)有意义,则解得14.A 解析 因为a=(2,1),b=(x,-2),a∥b,
所以2×(-2)-1×x=0,所以x=-4,
所以b=(-4,-2),所以a+b=(-2,-1),故选A.
5.C 解析 由α∈π,可知α为第三象限的角,故cos α<0,
由tan α=,
又sin2α+cos2α=1,解得cos α=-,故选C.
6.B 解析 由于函数y=x2+2x+a图象的对称轴为直线x=-1,且开口向上,所以x2+2x+a=0(a∈R)有正根,则必须f(0)<0,解得a<0,因为“a≤1”是“a<0”的必要不充分条件,故选B.
7.A 解析 因为圆锥底面半径为1,其侧面展开图是半圆,
所以圆锥的底面周长为2π,则圆锥的母线长为2,故圆锥的高为,
所以圆锥的体积为V=×π×12×,故选A.
8.D 解析 因为a=>e0=1,b=lnc>b,故选D.
9.C 解析 由题意可知=m,
两边取对数得-lg 5=(-lg 2),所以t=-1 350≈3 150,故选C.
10.A 解析 由f(x)=lg(x+)-可知,x∈R,
故f(x)+f(-x)=lg(x+)-+lg(-x+)-=lg(x+)(-x+)-=lg 1-2=-2,
即f(x)+1+f(-x)+1=0,令g(x)=f(x)+1,
则g(x)+g(-x)=0,即g(x)=f(x)+1为奇函数,
f(x)=lg(x+)-为增函数,则g(x)=f(x)+1为增函数,
不等式f(2x+1)+f(x)>-2,
即f(2x+1)+1+f(x)+1>0,
即g(2x+1)+g(x)>0,g(2x+1)>-g(x)=g(-x),
故2x+1>-x,x>-,即f(2x+1)+f(x)>-2的解集为-,+∞,故选A.
11.C 解析 由题可得,x+2y=1,则(x+1)+2(y+1)=4,
所以[(x+1)+2(y+1)]=5+≥5+2=,当且仅当,即x=y=时,等号成立,故选C.
12.A 解析 如图所示,取BC的中点O,连接OD,OA,分别取△BCD和△ABC的外心E与F,过两点分别作平面BDC和平面ABC的垂线,交于点P,则P就是外接球的球心,连接OP,DP,
则∠AOD为二面角A-BD-C的平面角,即∠AOD=60°,
则△AOD是等边三角形,其边长为6×=3,OE=OD=×3,在△POE中,∠POE=30°,
所以PE=OEtan 30°==1,
又由DE=OD=2,所以PD=R=,
所以四面体ABCD的外接球的表面积为4πR2=4π×()2=52π.故选A.
13.BD 解析 对于A,由b>a>0可得>0,A错误,
对于B,由a>b>0可得>0,B正确,
对于C,由b<00>,C错误,
对于D,由b,D正确,故选BD.
14.BC 解析 随机试验从袋中一次性取出2个球的样本空间含10个样本点,
随机事件A包含的样本点的个数为4,
所以P(A)=,A错误;
随机事件C包含的样本点的个数为9,所以P(C)=,B正确;
事件A与事件B不可能同时发生,所以事件A与事件B为互斥事件,
又因为P(A+B)=1,即事件A+B为必然事件,所以事件A与事件B是对立事件,C正确;
随机事件B包含的样本点的个数为6,所以P(B)=,随机事件AB为不可能事件,所以P(AB)=0,所以P(AB)≠P(A)P(B),
所以事件A与事件B不是相互独立事件,D错误.故选BC.
15.BCD 解析 A选项,若A>B,如A=,B=,2A=π,2B=,sin 2A=0,sin 2B=1,sin 2AB选项,S△ABC=bcsin A=1,bc=,
由余弦定理得cos A=,2bc·cos A=b2+c2-1,
2··cos A=b2+c2-1≥2bc-1=2·-1,
即-1,当且仅当b=c时等号成立,
由于在三角形中,sin A>0,所以4cos A≥4-sin A,cos A≥1-sin A>0,则cos2A≥1-sin A2,
又因为cos2A=1-sin2A,
即1-sin2A≥1-sin A2,
整理得sin A-1·sin A≤0,
解得0C选项,若a=2,b=4,A=,则bsin A=4×=2,所以bsin A所以满足条件的三角形有两个,所以C选项正确.
D选项,表示方向的单位向量;表示方向的单位向量,
根据平面向量加法的几何意义可知与∠BAC的角平分线共线,
由·=0可知∠BAC的角平分线与BC垂直,所以三角形ABC是等腰三角形.
而=1×1×cos A=cos A=>0,所以A为锐角,且A=,所以三角形ABC是等边三角形,所以选项D正确.故选BCD.
16.AC 解析 对于A选项,因为fx-=-f(x),所以f(x-3)=-fx-=f(x),所以3是函数f(x)的一个周期,故A正确;
对于B选项,因为fx+为奇函数,所以f-x+=-fx+,所以点,0是函数y=f(x)图象的对称中心,故B错误;
对于C选项,因为fx+为奇函数,所以f-x+=-fx+,所以f-x+=-f(x).
又因为fx-=-f(x),所以f-x+=fx-,所以f(-x)=f(x),
所以函数y=f(x)是偶函数,故C选项正确;
对于D选项,由选项C知,函数y=f(x)是偶函数,所以f(1)=f(-1)=-1.又因为3是函数y=f(x)的一个周期,所以f(2)=f(-1)=-1,f(3)=f(0)=2,f(2 023)=f(1)=-1,所以f(1)+f(2)+f(3)=0,所以f(1)+f(2)+f(3)+…+f(2 023)=×0-1=-1,故D错误.故选AC.
17.x2(答案不唯一)(形如f(x)=,m为正奇数,n为正偶数,都可以) 解析 因为f(x)是幂函数,且f(x)在(0,+∞)内单调递增,故可设f(x)=(m,n∈N*,m,n互质),
又因为f(-x)=f(x),所以m为奇数,n为偶数,
故f(x)=x2为符合条件的一个函数.
18.-3 -,- 解析 因为a=(2,1),b为单位向量,
则|a|=,|b|=1,
因为(a+2b)⊥(a-b),则(a+2b)·(a-b)=a2+a·b-2b2=5+a·b-2=0,可得a·b=-3,
所以向量b在向量a上的投影向量为|b|cos··a=-a=-(2,1)=-,-.
19.9 解析 由频率分布直方图的频率和为1,可得0.005×10+0.022 5×10+a×10+0.035×10+0.007 5×10=1,
解得a=0.030.
故成绩不低于85分的人的频率为×10+0.007 5×10=0.225,所以成绩不低于85分的人数有0.225×40=9.
20. 解析 因为f(x)=sin ωx-cos ωx=2sinωx-,
当00,则-<ωx-,
因为函数f(x)在0,内存在最值,则,解得ω>,当因为函数f(x)在,π内单调,
则,πω- kπ-,kπ+(k∈Z),
所以其中k∈Z,
解得k-≤ω≤k+(k∈Z),
所以k-≤k+,解得k≤,
又因为ω>0,则k∈{0,1,2},当k=0时,0<ω≤;当k=1时,≤ω≤;当k=2时,≤ω≤.
又因为ω>,因此,实数ω的取值范围是.
21.解 (1)由,
得2sin Bcos C-sin Bcos A=sin Acos B-2sin Ccos B,
所以2sin(B+C)=sin(A+B),
则2sin A=sin C,所以.
(2)由sin B=,且2sin A=sin C,
则cos B=±,
设a=x c=2x,则b2=a2+c2-2accos B 4=x2+4x2-4x2cos B,
所以x=1或x=,
又因为S=acsin B=x2sin B,
当x=1时,S=;当x=时,S=.
22.
(1)证明 取PA的中点F,连接EF,BF,∵E是PD的中点,∴EF∥AD且EF=AD,
又BC∥AD且BC=AD,
∴BC∥EF且BC=EF,
∴四边形BCEF为平行四边形,CE∥BF,
又CE 平面PAB,BF 平面PAB,∴CE∥平面PAB.
(2)解 取AD的中点G,连接EG,过点G作GH⊥AC交AC于点H,连接EH,
∵E,G分别是PD,AD的中点,∴EG∥PA.
又PA⊥平面ABCD,
∴EG⊥平面ABCD,AC 平面ABCD,∴EG⊥AC,
又AC⊥HG,HG∩EG=G,HG,EG 平面EGH,
∴AC⊥平面EGH,HE 平面EGH,
∴AC⊥HE,∴∠EHG是平面EAC与平面DAC的夹角的平面角.∴∠EHG=45°.
∵AB=2,BC=1,∴tan∠CAB=,
∴tan∠HAG=2,
∴sin∠HAG=,∴GH=AG·sin∠GAH=1×,∴EG=HG=.
∴VE-ACD=×EG×S△ACD=×2×2=.
23.解 (1)f(1)=2 log2(5m-11)=log24 5m-11=4 m=3.
(2)方程g(x)-f(x)=0
由①可得(3m-6)x2+(m-5)x-1=0 (3x+1)·[(m-2)x-1]=0,
当m=2时,方程有唯一解x=-,此时+m=-3+2=-1<0,∴不满足②,
当m=-1时,方程有两个相等解x==-,此时+m=-3-1=-4<0,∴不满足②.
当m≠-1且m≠2时,方程有两个不等解x1=-,x2=,
若x2=满足m-2+m=2m-2>0 m>1,
若x1=-满足+m=-3+m>0 m>3,
则若x=是唯一解,有解得1若x=-是唯一解,则有解得m∈ ,
综上,当1(3)当x1,x2∈[t,t+1]时,|g(x1)-g(x2)|≤1恒成立,则有g(x)max-g(x)min≤1,
由已知m>0,由复合函数的单调性知g(x)=log2+m在(0,+∞)内单调递减,
∴g(t)-g(t+1)≤1 log2+m-log2+m≤1=log22 +m≤+2m,
∴mt2+(m+1)t-1≥0对 t∈,2恒成立,令h(t)=mt2+(m+1)t-1.
∵m>0,
∴h(t)在t∈,2上单调递增,
∴h(t)min=h=≥0 m≥,
∴实数m的取值范围是,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024普通高中学业水平考试数学模拟卷(四)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知集合A={1,2,3},B={2,4},则A∪B=( )
A.{2} B.{2,3,4} C.{1,2,3,4} D.{0,2,3,4}
2.已知i为虚数单位,则复数(1+2i)+(-3+2i)在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.函数f(x)=+lg(x-1)的定义域为( )
A.{x|x≥2} B.{x|x<1} C.{x|1≤x≤2} D.{x|1
A.(-2,-1) B.(2,1) C.(3,-1) D.(-3,1)
5.已知α∈π,,且tan α=,则cos α=( )
A.- B. C.- D.
6.“a≤1”是“方程x2+2x+a=0(a∈R)有正实数根”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知圆锥的底面半径为1,其侧面展开图是半圆,则该圆锥的体积为( )
A. B.π C. D.2π
8.已知a=,b=ln,c=sin,则( )
A.a>b>c B.b>c>a C.c>a>b D.a>c>b
9.现测得某放射性元素的半衰期为1 350年(每经过1 350年,该元素的存量为原来的一半),某生物标本中该放射性元素的初始存量为m,经检测现在的存量为.据此推测该生物距今约为( )(参考数据:lg 2≈0.3)
A.2 452年 B.2 750年 C.3 150年 D.3 856年
10.已知函数f(x)=lg(x+)-,则不等式f(2x+1)+f(x)>-2的解集为( )
A.-,+∞ B.-,100 C.-∞,- D.-,100
11.已知正实数x,y满足x+2y=1,则的最小值为( )
A. B. C. D.
12.在四面体ABCD中,△ABC与△BCD都是边长为6的等边三角形,且二面角A-BC-D的大小为60°,则四面体ABCD外接球的表面积是( )
A.52π B.54π
C.56π D.60π
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.已知a,b∈R,则下列选项中能使成立的是( )
A.b>a>0 B.a>b>0
C.b<014.不透明的袋中装有5个大小质地完全相同的小球,其中3个红球、2个白球,从袋中一次性取出2个球,记事件A=“两球同色”,事件B=“两球异色”,事件C=“至少有一红球”,则( )
A.P(A)= B.P(C)=
C.事件A与事件B是对立事件 D.事件A与事件B是相互独立事件
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,则( )
A.若A>B,则sin 2A>sin 2B
B.若S△ABC=1,a=1,则sin A的最大值为
C.若a=2,b=4,A=,则满足条件的三角形有两个
D.若·=0,且,则△ABC为等边三角形
16.已知定义在R上的函数y=f(x)满足fx-=-f(x),且fx+为奇函数,f(-1)=-1,f(0)=2.下列说法正确的是( )
A.3是函数y=f(x)的一个周期
B.函数y=f(x)的图象关于直线x=对称
C.函数y=f(x)是偶函数
D.f(1)+f(2)+f(3)+…+f(2 023)=2
三、填空题(本大题共4小题,共15分)
17.已知f(x)是幂函数,且满足:①f(-x)=f(x);②f(x)在(0,+∞)内单调递增,请写出符合上述条件的一个函数f(x)= .
18.已知a=(2,1),b为单位向量,且(a+2b)⊥(a-b),则a·b= ,向量b在向量a上的投影向量为 .
19.某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示,成绩不低于85分的人数有 人.
20.已知函数f(x)=sin ωx-cos ωx(ω>0)在0,内存在最值,且在,π内单调,则ω的取值范围是 .
四、解答题(本大题共3小题,共33分)
21.(11分)在△ABC中,角A,B,C的对边分别为a,b,c,若满足.
(1)求的值;
(2)若sin B=,b=2,求△ABC的面积.
22.(11分) 已知四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AB=AD=2BC=2,E为PD的中点.
(1)求证:CE∥平面PAB;
(2)设平面EAC与平面DAC的夹角为45°,求三棱锥E-ACD的体积.
23.(11分)已知函数f(x)=log2[(3m-6)x+2m-5],g(x)=log2+m,m∈R.
(1)若f(1)=2,求m的值;
(2)若方程g(x)-f(x)=0恰有一个实根,求m的取值范围;
(3)设m>0,若对任意t∈,2,当x1,x2∈[t,t+1]时,满足|g(x1)-g(x2)|≤1,求m的取值范围.
普通高中学业水平考试数学模拟卷(四)
1.C
2.B 解析 因为(1+2i)+(-3+2i)=-2+4i,所以该复数在复平面内对应的点的坐标为(-2,4),位于第二象限.故选B.
3.D 解析 由题意,要使f(x)有意义,则解得1
所以2×(-2)-1×x=0,所以x=-4,
所以b=(-4,-2),所以a+b=(-2,-1),故选A.
5.C 解析 由α∈π,可知α为第三象限的角,故cos α<0,
由tan α=,
又sin2α+cos2α=1,解得cos α=-,故选C.
6.B 解析 由于函数y=x2+2x+a图象的对称轴为直线x=-1,且开口向上,所以x2+2x+a=0(a∈R)有正根,则必须f(0)<0,解得a<0,因为“a≤1”是“a<0”的必要不充分条件,故选B.
7.A 解析 因为圆锥底面半径为1,其侧面展开图是半圆,
所以圆锥的底面周长为2π,则圆锥的母线长为2,故圆锥的高为,
所以圆锥的体积为V=×π×12×,故选A.
8.D 解析 因为a=>e0=1,b=ln
9.C 解析 由题意可知=m,
两边取对数得-lg 5=(-lg 2),所以t=-1 350≈3 150,故选C.
10.A 解析 由f(x)=lg(x+)-可知,x∈R,
故f(x)+f(-x)=lg(x+)-+lg(-x+)-=lg(x+)(-x+)-=lg 1-2=-2,
即f(x)+1+f(-x)+1=0,令g(x)=f(x)+1,
则g(x)+g(-x)=0,即g(x)=f(x)+1为奇函数,
f(x)=lg(x+)-为增函数,则g(x)=f(x)+1为增函数,
不等式f(2x+1)+f(x)>-2,
即f(2x+1)+1+f(x)+1>0,
即g(2x+1)+g(x)>0,g(2x+1)>-g(x)=g(-x),
故2x+1>-x,x>-,即f(2x+1)+f(x)>-2的解集为-,+∞,故选A.
11.C 解析 由题可得,x+2y=1,则(x+1)+2(y+1)=4,
所以[(x+1)+2(y+1)]=5+≥5+2=,当且仅当,即x=y=时,等号成立,故选C.
12.A 解析 如图所示,取BC的中点O,连接OD,OA,分别取△BCD和△ABC的外心E与F,过两点分别作平面BDC和平面ABC的垂线,交于点P,则P就是外接球的球心,连接OP,DP,
则∠AOD为二面角A-BD-C的平面角,即∠AOD=60°,
则△AOD是等边三角形,其边长为6×=3,OE=OD=×3,在△POE中,∠POE=30°,
所以PE=OEtan 30°==1,
又由DE=OD=2,所以PD=R=,
所以四面体ABCD的外接球的表面积为4πR2=4π×()2=52π.故选A.
13.BD 解析 对于A,由b>a>0可得>0,A错误,
对于B,由a>b>0可得>0,B正确,
对于C,由b<0
对于D,由b
14.BC 解析 随机试验从袋中一次性取出2个球的样本空间含10个样本点,
随机事件A包含的样本点的个数为4,
所以P(A)=,A错误;
随机事件C包含的样本点的个数为9,所以P(C)=,B正确;
事件A与事件B不可能同时发生,所以事件A与事件B为互斥事件,
又因为P(A+B)=1,即事件A+B为必然事件,所以事件A与事件B是对立事件,C正确;
随机事件B包含的样本点的个数为6,所以P(B)=,随机事件AB为不可能事件,所以P(AB)=0,所以P(AB)≠P(A)P(B),
所以事件A与事件B不是相互独立事件,D错误.故选BC.
15.BCD 解析 A选项,若A>B,如A=,B=,2A=π,2B=,sin 2A=0,sin 2B=1,sin 2A
由余弦定理得cos A=,2bc·cos A=b2+c2-1,
2··cos A=b2+c2-1≥2bc-1=2·-1,
即-1,当且仅当b=c时等号成立,
由于在三角形中,sin A>0,所以4cos A≥4-sin A,cos A≥1-sin A>0,则cos2A≥1-sin A2,
又因为cos2A=1-sin2A,
即1-sin2A≥1-sin A2,
整理得sin A-1·sin A≤0,
解得0
D选项,表示方向的单位向量;表示方向的单位向量,
根据平面向量加法的几何意义可知与∠BAC的角平分线共线,
由·=0可知∠BAC的角平分线与BC垂直,所以三角形ABC是等腰三角形.
而=1×1×cos A=cos A=>0,所以A为锐角,且A=,所以三角形ABC是等边三角形,所以选项D正确.故选BCD.
16.AC 解析 对于A选项,因为fx-=-f(x),所以f(x-3)=-fx-=f(x),所以3是函数f(x)的一个周期,故A正确;
对于B选项,因为fx+为奇函数,所以f-x+=-fx+,所以点,0是函数y=f(x)图象的对称中心,故B错误;
对于C选项,因为fx+为奇函数,所以f-x+=-fx+,所以f-x+=-f(x).
又因为fx-=-f(x),所以f-x+=fx-,所以f(-x)=f(x),
所以函数y=f(x)是偶函数,故C选项正确;
对于D选项,由选项C知,函数y=f(x)是偶函数,所以f(1)=f(-1)=-1.又因为3是函数y=f(x)的一个周期,所以f(2)=f(-1)=-1,f(3)=f(0)=2,f(2 023)=f(1)=-1,所以f(1)+f(2)+f(3)=0,所以f(1)+f(2)+f(3)+…+f(2 023)=×0-1=-1,故D错误.故选AC.
17.x2(答案不唯一)(形如f(x)=,m为正奇数,n为正偶数,都可以) 解析 因为f(x)是幂函数,且f(x)在(0,+∞)内单调递增,故可设f(x)=(m,n∈N*,m,n互质),
又因为f(-x)=f(x),所以m为奇数,n为偶数,
故f(x)=x2为符合条件的一个函数.
18.-3 -,- 解析 因为a=(2,1),b为单位向量,
则|a|=,|b|=1,
因为(a+2b)⊥(a-b),则(a+2b)·(a-b)=a2+a·b-2b2=5+a·b-2=0,可得a·b=-3,
所以向量b在向量a上的投影向量为|b|cos
19.9 解析 由频率分布直方图的频率和为1,可得0.005×10+0.022 5×10+a×10+0.035×10+0.007 5×10=1,
解得a=0.030.
故成绩不低于85分的人的频率为×10+0.007 5×10=0.225,所以成绩不低于85分的人数有0.225×40=9.
20. 解析 因为f(x)=sin ωx-cos ωx=2sinωx-,
当0
因为函数f(x)在0,内存在最值,则,解得ω>,当
则,πω- kπ-,kπ+(k∈Z),
所以其中k∈Z,
解得k-≤ω≤k+(k∈Z),
所以k-≤k+,解得k≤,
又因为ω>0,则k∈{0,1,2},当k=0时,0<ω≤;当k=1时,≤ω≤;当k=2时,≤ω≤.
又因为ω>,因此,实数ω的取值范围是.
21.解 (1)由,
得2sin Bcos C-sin Bcos A=sin Acos B-2sin Ccos B,
所以2sin(B+C)=sin(A+B),
则2sin A=sin C,所以.
(2)由sin B=,且2sin A=sin C,
则cos B=±,
设a=x c=2x,则b2=a2+c2-2accos B 4=x2+4x2-4x2cos B,
所以x=1或x=,
又因为S=acsin B=x2sin B,
当x=1时,S=;当x=时,S=.
22.
(1)证明 取PA的中点F,连接EF,BF,∵E是PD的中点,∴EF∥AD且EF=AD,
又BC∥AD且BC=AD,
∴BC∥EF且BC=EF,
∴四边形BCEF为平行四边形,CE∥BF,
又CE 平面PAB,BF 平面PAB,∴CE∥平面PAB.
(2)解 取AD的中点G,连接EG,过点G作GH⊥AC交AC于点H,连接EH,
∵E,G分别是PD,AD的中点,∴EG∥PA.
又PA⊥平面ABCD,
∴EG⊥平面ABCD,AC 平面ABCD,∴EG⊥AC,
又AC⊥HG,HG∩EG=G,HG,EG 平面EGH,
∴AC⊥平面EGH,HE 平面EGH,
∴AC⊥HE,∴∠EHG是平面EAC与平面DAC的夹角的平面角.∴∠EHG=45°.
∵AB=2,BC=1,∴tan∠CAB=,
∴tan∠HAG=2,
∴sin∠HAG=,∴GH=AG·sin∠GAH=1×,∴EG=HG=.
∴VE-ACD=×EG×S△ACD=×2×2=.
23.解 (1)f(1)=2 log2(5m-11)=log24 5m-11=4 m=3.
(2)方程g(x)-f(x)=0
由①可得(3m-6)x2+(m-5)x-1=0 (3x+1)·[(m-2)x-1]=0,
当m=2时,方程有唯一解x=-,此时+m=-3+2=-1<0,∴不满足②,
当m=-1时,方程有两个相等解x==-,此时+m=-3-1=-4<0,∴不满足②.
当m≠-1且m≠2时,方程有两个不等解x1=-,x2=,
若x2=满足m-2+m=2m-2>0 m>1,
若x1=-满足+m=-3+m>0 m>3,
则若x=是唯一解,有解得1
综上,当1
由已知m>0,由复合函数的单调性知g(x)=log2+m在(0,+∞)内单调递减,
∴g(t)-g(t+1)≤1 log2+m-log2+m≤1=log22 +m≤+2m,
∴mt2+(m+1)t-1≥0对 t∈,2恒成立,令h(t)=mt2+(m+1)t-1.
∵m>0,
∴h(t)在t∈,2上单调递增,
∴h(t)min=h=≥0 m≥,
∴实数m的取值范围是,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
