2024普通高中学业水平考试数学模拟卷6(含解析)
文档属性
| 名称 | 2024普通高中学业水平考试数学模拟卷6(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 424.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:28:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024普通高中学业水平考试数学模拟卷(六)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知集合A={0,1,2},B={0,2,4},则A∪B=( )
A. B.{0,2}
C.{1,4} D.{0,1,2,4}
2.函数y=ln(x+1)的定义域是( )
A.(-1,+∞) B.[-1,+∞)
C.(0,+∞) D.[0,+∞)
3.设命题p: n∈N,n2>2n+5,则p的否定为( )
A. n∈N,n2>2n+5 B. n∈N,n2≤2n+5
C. n∈N,n2≤2n+5 D. n∈N,n2=2n+5
4.设α∈R,则sinα-=( )
A.sin α B.-sin α C.cos α D.-cos α
5.已知a,b∈R,则“|a-b|<1”是“|a|+|b|<1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.已知向量a=(m,1),b=(2,-3),若a⊥b,则实数m=( )
A.- B. C. D.-
7.若数据x1,x2,…,xn的平均数为,方差为s2,则5x1+2,5x2+2,…,5xn+2的平均数和方差分别为( )
A.,s2 B.5+2,s2 C.5+2,25s2 D.,25s2
8.为得到函数y=sin 2x的图象,只需将函数y=sin2x-的图象( )
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D.向左平移个单位
9.科学研究已经证实,人的智力、情绪和体力分别以33天、28天和23天为周期,按y=sin(ωx+φ)进行变化,记智力曲线为I,情绪曲线为E,体力曲线为P,且现在三条曲线都处于x轴的同一点处,那么第322天时( )
A.智力曲线I处于最低点
B.情绪曲线E与体力曲线P都处于上升期
C.智力曲线I与情绪曲线E相交
D.情绪曲线E与体力曲线P都关于(322,0)对称
10.两条异面直线与同一平面所成的角,不可能是( )
A.两个角均为锐角 B.一个角为0°,一个角为90°
C.两个角均为0° D.两个角均为90°
11.已知定义在R上的函数f(x)满足:f(x)为奇函数,f(x+1)为偶函数,当0≤x≤1时,f(x)=2x-1,则f(log22 024)等于( )
A.- B. C.- D.
12.在三棱锥A-BCD中,平面ACD⊥平面BCD,△ACD是以CD为斜边的等腰直角三角形,AB⊥BC,AC=2CB=4,则该三棱锥的外接球的半径为( )
A.2 B.
C.2 D.
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.关于复数z=x+yi(x,y∈R,i为虚数单位),下列说法正确的是( )
A.z2=x2+y2 B.若|z-2i|=2,则x2+(y-2)2=4
C.若zi为纯虚数,则x≠0,y=0 D.|z|>(|x|+|y|)
14.已知函数f(x)=2x-2-x,函数g(x)=ln,则下列说法中正确的是( )
A.f(x)·g(x)是偶函数
B.f(x)·|g(x)|是奇函数
C.|f(x)|·g(x)是偶函数
D.|f(x)·g(x)|是偶函数
15.下列说法正确的是( )
A.若事件A,B互斥,则P(A∪B)=P(A)+P(B)
B.若事件A,B相互独立,则P()=P()P()
C.若事件A,B,C两两互斥,则P(A∪B∪C)=P(A)+P(B)+P(C)
D.若事件A,B,C两两独立,则P(ABC)=P(A)P(B)P(C)
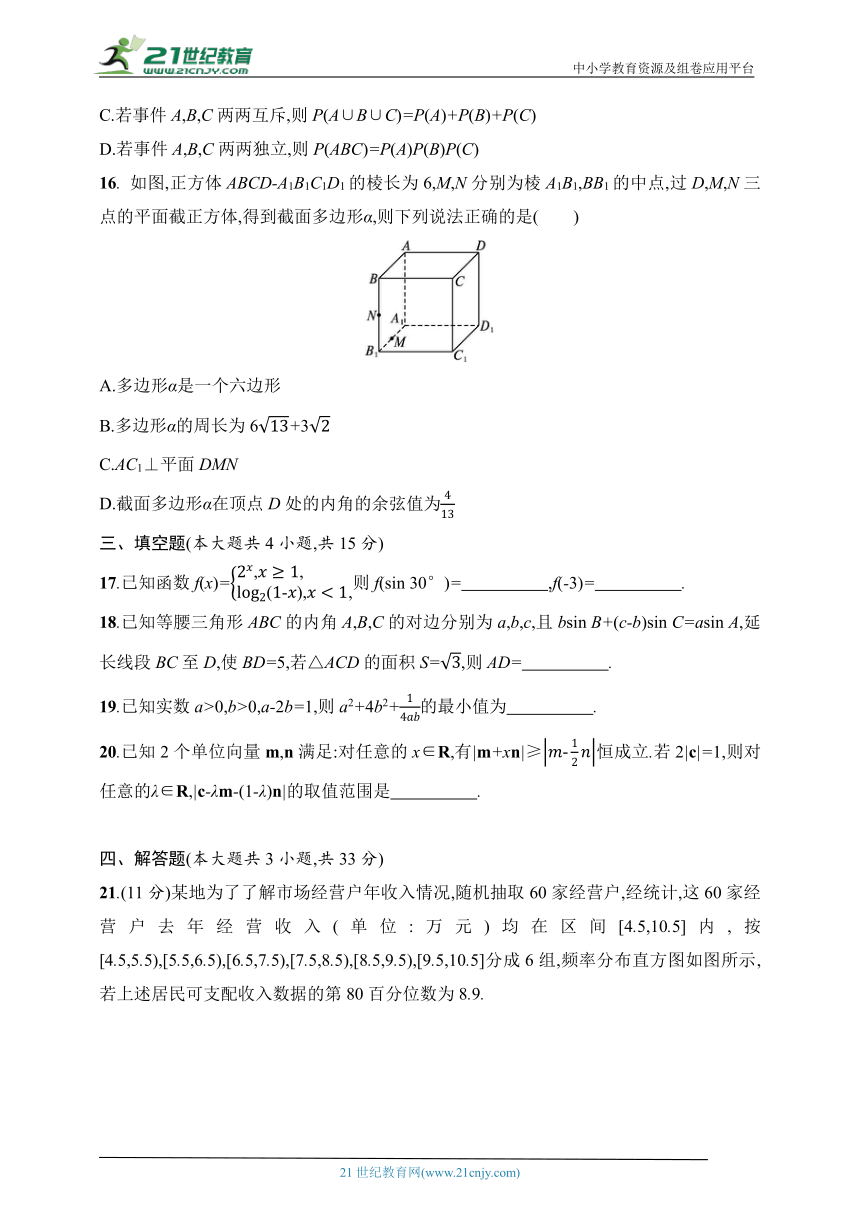
16. 如图,正方体ABCD-A1B1C1D1的棱长为6,M,N分别为棱A1B1,BB1的中点,过D,M,N三点的平面截正方体,得到截面多边形α,则下列说法正确的是( )
A.多边形α是一个六边形
B.多边形α的周长为6+3
C.AC1⊥平面DMN
D.截面多边形α在顶点D处的内角的余弦值为
三、填空题(本大题共4小题,共15分)
17.已知函数f(x)=则f(sin 30°)= ,f(-3)= .
18.已知等腰三角形ABC的内角A,B,C的对边分别为a,b,c,且bsin B+(c-b)sin C=asin A,延长线段BC至D,使BD=5,若△ACD的面积S=,则AD= .
19.已知实数a>0,b>0,a-2b=1,则a2+4b2+的最小值为 .
20.已知2个单位向量m,n满足:对任意的x∈R,有|m+xn|≥恒成立.若2|c|=1,则对任意的λ∈R,|c-λm-(1-λ)n|的取值范围是 .
四、解答题(本大题共3小题,共33分)
21.(11分)某地为了了解市场经营户年收入情况,随机抽取60家经营户,经统计,这60家经营户去年经营收入(单位:万元)均在区间[4.5,10.5]内,按[4.5,5.5),[5.5,6.5),[6.5,7.5),[7.5,8.5),[8.5,9.5),[9.5,10.5]分成6组,频率分布直方图如图所示,若上述居民可支配收入数据的第80百分位数为8.9.
(1)求a,b的值;
(2)估计这60家经营户年收入的平均值(同一组中的数据用该区间的中点值作代表);
(3)用分层抽样的方法在收入区间为[6.5,8.5)的经营户中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1户在收入区间为[7.5,8.5)内的概率.
22.(11分)如图,在三棱锥P-ABC中,PA⊥AC,AB⊥BC,PA=6,AB=BC=8.设D,E,F分别为棱PC,AC,AB的中点,且DF=5.
(1)求证:平面DEF⊥平面ABC;
(2)求平面PBC与平面PAC所成角的正弦值.
23.(11分)已知函数f(x)=ax2-|x-a|,a∈R.
(1)当a=1时,求函数f(x)的单调递增区间(不必写明证明过程);
(2)判断函数f(x)的奇偶性,并说明理由;
(3)当-1≤a≤2时,若对任意的x∈[1,3],恒有f(x)+bx≤0成立,求a2+3b的最大值.
普通高中学业水平考试数学模拟卷(六)
1.D 解析 由题知A∪B={0,1,2}∪{0,2,4}={0,1,2,4},故选D.
2.A
3.B 解析 因为命题p: n∈N,n2>2n+5,
所以p的否定 p: n∈N,n2≤2n+5,故选B.
4.D 解析 sinα-=-sin-α=-cos α,故选D.
5.B
6.C 解析 ∵a=(m,1),b=(2,-3)且a⊥b,则a·b=2m-3=0,解得m=.
故选C.
7.C
8.D 解析 因为将函数y=sin2x-的图象向左平移个单位,则y=sin2x+-=sin 2x.
故选D.
9.D 解析 当第322天时,322除33余25,322除28余14,322除23余0,即智力曲线I位于周期处,情绪曲线E位于周期处,体力曲线P刚好位于起始点处,
A选项,因为,则智力曲线I不处于最低点,故A错误;
B选项,情绪曲线E处于最高点,即将开始下降,故B错误;
C选项,经过n个周期后,因为周期不同,所以智力曲线I与情绪曲线E不一定相交,故C错误;
D选项,(322,0)位于体力曲线P和情绪曲线E的交点x轴上,故D正确,故选D.
10.D 解析 对于A,两个角可能均为锐角,故A不符合题意;
对于B,可能一个角为0°,一个角为90°,故B不符合题意;
对于C,可能两个角均为0°,故C不符合题意;
对于D,如果两个角均为90°,则两条直线垂直于同一个平面,则这两条直线平行,不是异面直线,故这两个角不可能均为90°,故D符合题意.故选D.
11.A 解析 定义在R上的函数f(x)满足f(x)为奇函数,f(x+1)为偶函数,可得f(-x)=-f(x),f(-x+1)=f(x+1) f(-x)=f(x+2),则f(x+2)=-f(x),故f(x+4)=-f(x+2)=f(x),可得f(x)的最小正周期为4,
由于log22 024∈(10,11),则log22 024-12∈(-2,-1),(log22 024-12)+2∈(0,1),
当0≤x≤1时,f(x)=2x-1,
所以f(log22 024-12+2)=-1=2-10×-1=2 024×2-10-1=-1,
则f(log22 024)=f(log22 024-12)=-f(log22 024-10)=-(-1)=1-=1-=-.
故选A.
12. B 解析 设CD中点为M,连接AM,
因为△ACD是以CD为斜边的等腰直角三角形,AC=2CB=4,
所以AM=DM=CM=2,AM⊥CD,过点M作MN⊥CD,
因为平面ACD⊥平面BCD,平面ACD∩平面BCD=CD,MN 平面BCD,AM 平面ACD,
所以MN⊥平面ACD,AM⊥平面BCD,
所以三棱锥的外接球的球心在MN上,
设外接球的半径为R,
则由AB⊥BC得AB=2,
由AM⊥BM得BM=2=BC,
又因为BM2+BC2=CM2,
所以△BCM为等腰直角三角形,
设球心为O,CM中点为P,连接BP,
则MP=CP=BP=,
所以OM=-BP,
即,解得R=,故选B.
13.BC 解析 z2=(x+yi)2=x2+2xyi+y2i2=x2-y2+2xyi,故选项A错误;
|z-2i|=2,由几何意义可得(x,y)到(0,2)的距离为2,
进而可得,=2,即x2+(y-2)2=4,故选项B正确;
zi=(x+yi)i=-y+xi且为纯虚数,x≠0,y=0,故选项C正确;
|z|=,可取x=,y=,则|z|=(|x|+|y|)=×=,|z|=(|x|+|y|),选项D错误.
故选BC.
14.ABD 解析 函数f(x)=2x-2-x的定义域为R,函数g(x)=ln的定义域为(-1,1),f(-x)=2-x-2x=-f(x),g(-x)=ln=-ln=-g(x),
对于A,函数f(x)·g(x)的定义域为(-1,1),f(-x)·g(-x)=f(x)·g(x),f(x)·g(x)是偶函数,A正确;
对于B,函数f(x)·|g(x)|的定义域为(-1,1),f(-x)·|g(-x)|=-f(x)·|g(x)|,f(x)·|g(x)|是奇函数,B正确;
对于C,函数|f(x)|·g(x)的定义域为(-1,1),|f(-x)|·g(-x)=-|f(x)|·g(x),|f(x)|·g(x)是奇函数,C错误;
对于D,函数|f(x)·g(x)|的定义域为(-1,1),|f(-x)·g(-x)|=|f(x)·g(x)|,|f(x)·g(x)|是偶函数,D正确.
故选ABD.
15.ABC 解析 对于A,根据互斥事件的概率加法公式即可判断A正确;
对于B,若事件A,B相互独立,则也相互独立,所以P()=P()P(),故B正确;
对于C,根据互斥事件的概率加法公式即可判断C正确;
对于D,例如,从1,2,3,4中随机选出一个数字,记事件A=“取出的数字为1或2”,B=“取出的数字为1或3”,C=“取出的数字为1或4”,则AB=AC=BC=ABC=“取出的数字为1”,
显然P(A)=P(B)=P(C)=,
P(AB)=P(AC)=P(BC)=P(ABC)=,
满足P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C),
所以事件A,B,C两两独立,但是P(ABC)≠P(A)·P(B)P(C),故D错误.
故选ABC.
16. BD 解析 延长MN,AB相交于Q,连接DQ交BC于E,连接NE,
则由△BNQ≌△B1NM可得BQ=B1M=3,又△QBE∽△QAD,
∴ BE=2,
取B1H=2,连接D1H,过M作MF∥D1H,连接DF,
由于EH∥B1B,EH=B1B,
又DD1∥B1B,DD1=B1B,
∴EH∥D1D,EH=D1D,四边形DD1HE为平行四边形,故ED∥HD1,
又MF∥HD1,
∴MF∥ED,
根据,
∴NE∥DF,
则五边形MNEDF即为截面多边形,故A错误;
由MF∥D1H可知A1F=2,
∴五边形MNEDF的周长为MN+NE+ED+DF+MF=3=6+3,故B正确;
由于B1D1⊥A1C1,B1D1⊥A1A,且A1C1∩A1A=A1,A1C1,A1A 平面A1C1A,
∴B1D1⊥平面A1C1A,C1A 平面A1C1A,
∴C1A⊥D1B1,
若AC1⊥平面DMN,MF 平面DMN,则AC1⊥MF,MF∥D1H,故AC1⊥D1H,D1H∩D1B1=D1,D1H,D1B1 平面D1B1H,故AC1⊥平面D1B1H,这显然是不成立的,故AC1与平面DMN不垂直,故C错误;
连接EF,EH,HF,由于EH∥BB1,EH=BB1,HF∥A1B1,HF=A1B1,
∴四边形BEHB1,A1B1HF均为平行四边形,则EF==6,
cos∠EDF=,故D正确,故选BD.
17.-1 2 解析 因为f(x)=
则f(sin 30°)=f=log21-=-1,
f(-3)=log2(1+3)=2.
18. 解析 由正弦定理,b2+(c-b)c=a2,即bc=b2+c2-a2,
故cos A=,
又因为A∈(0,π),
故A=,
所以△ABC是等边三角形.
又因为△ACD的面积S=CA·CDsin∠ACD=,
故S=CA·(5-CA)·,
解得(CA-1)(CA-4)=0,
解得AC=1或AC=4.
当AC=1时,CD=5-1=4,当AC=4时,CD=5-4=1,
故AD2=CA2+CD2-2CA·CDcos=1+16+4=21,故AD=.
19.3 解析 实数a>0,b>0,a-2b=1,则a2+4b2+=(a-2b)2+4ab+≥1+2=3,
当且仅当b=,a=时,等号成立,
a2+4b2+的最小值为3.
20.,+∞ 解析 因为对任意的x∈R,有|m+xn|≥恒成立,所以(m+xn)2≥m-n2恒成立,
即m2+2xm·n+x2n2≥m2-m·n+n2恒成立,
又因为m,n为单位向量,所以x2+2xm·n+m·n-≥0恒成立,
所以Δ=(2m·n)2-4m·n-=4(m·n)2-4m·n+1=(2m·n-1)2≤0,
所以2m·n-1=0,所以m·n=,设m与n的夹角为θ,则m·n=|m||n|cos θ=cos θ=,
又因为θ∈[0,π],所以θ=,不妨设m==(1,0),n==,c==(x,y),
因为2|c|=1,所以x2+y2=,所以点C在以坐标原点为圆心,半径r=的圆上,
设=λm+(1-λ)n=λ+(1-λ),
则D在直线AB上,
又因为直线AB的方程为y=(x-1),
即x+y-=0,
所以c-λm-(1-λ)n=,
所以|c-λm-(1-λ)n|=||,
又因为O到直线AB的距离d=,
所以||≥-r=,
即|c-λm-(1-λ)n|的取值范围是,+∞.
21.解 (1)依题意得0.10+0.15+0.15+a+b+0.05=1,
即a+b=0.55,
又第80百分位数在[8.5,9.5),
∴0.05+0.6b=1-0.8,解得a=0.3,b=0.25.
(2)=5×0.1+6×0.15+7×0.15+8×0.3+9×0.25+10×0.05=7.6.
(3)在[6.5,7.5)有9户,在[7.5,8.5)有18户,
所以在[6.5,7.5)内抽取2户,在[7.5,8.5)内抽取4户,
设在[6.5,7.5)内抽取的2户为A1,A2,在[7.5,8.5)内抽取的4户为B1,B2,B3,B4,
任取2户的所有情况为A1A2,A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4,B1B2,B1B3,B1B4,B2B3,B2B4,B3B4,共15种情况,
其中至多有1户在[7.5,8.5)内的样本点包含A1A2,A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4,共9个,
设至多有1户在[7.5,8.5)内为事件A,则P(A)=.
22.(1)证明 由PA⊥AC,D,E分别为棱PC,AC的中点,得DE∥PA,DE⊥AC,
AB=BC=8,D,E,F分别为棱PC,AC,AB的中点,且EF=4,DE=3,DF=5,
DF2=DE2+EF2,DE⊥EF,EF 平面ABC,AC 平面ABC,EF∩AC=E,
∴DE⊥平面ABC,DE 平面DEF.
∴平面DEF⊥平面ABC.
(2)解 连接BE,则由AB=BC,BE⊥AC,得DE⊥BE,DE∩AC=E,DE 平面ABC,AC 平面ABC,
∴DE⊥平面ABC,
过点B作BH⊥PC,垂足为H,连接EH,
则∠EHB是二面角B-PC-A的平面角.
于是PB=10,BC=8,PC=2,
∴BH=,
∵AB=BC=8,AC=8,
∴BE=4,
∴sin∠EHB=.
23.解 (1)当a=1时,f(x)=x2-|x-1|=
由二次函数的性质可知,当x≥1时,f(x)=x2-x+1,此时f(x)在[1,+∞)内单调递增,当x<1时,f(x)=x2+x-1,f(x)在-,1内单调递增,
故f(x)的单调递增区间为-,+∞.
(2)当a=0时,f(x)=-|x|,对于 x∈R,f(-x)=-|x|=f(x),
故f(x)为偶函数,
当a≠0时,f(0)=-|a|≠0,故f(x)不是奇函数,
又f(1)=a-|1-a|,f(-1)=a-|1+a|,显然|1-a|≠|1+a|,
即f(1)≠f(-1),故f(x)不是偶函数,
综上所述,当a=0时,f(x)是偶函数,当a≠0时,f(x)既不是偶函数又不是奇函数.
(3)①当-1≤a≤1时,“f(x)+bx≤0在[1,3]上恒成立”等价于“ax2+(b-1)x+a≤0在[1,3]上恒成立”,也就是b≤-ax++1恒成立,
由于y=x+在[1,3]上单调递增,
若0≤a≤1,则y=-ax++1在[1,3]上单调递减,
故当x=3时,y=-ax++1取最小值,
则-ax++1min=1-a,所以b≤1-a,
故a2+3b≤a2-10a+3≤3;
若-1≤a<0,则y=-ax++1在[1,3]上单调递增,-ax++1min=1-2a,
所以b≤1-2a,
于是a2+3b≤a2-6a+3≤10,当a=-1,b=3时,等号成立.
②当1由于函数y=x-在[1,3]上单调递增,
所以y=-ax--1在[1,3]上单调递减,
当1当a当1故b≤1-a,a2+3b≤a2-10a+3<-6.
综上所述,a2+3b的最大值为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024普通高中学业水平考试数学模拟卷(六)
(时间:80分钟,满分:100分)
一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)
1.已知集合A={0,1,2},B={0,2,4},则A∪B=( )
A. B.{0,2}
C.{1,4} D.{0,1,2,4}
2.函数y=ln(x+1)的定义域是( )
A.(-1,+∞) B.[-1,+∞)
C.(0,+∞) D.[0,+∞)
3.设命题p: n∈N,n2>2n+5,则p的否定为( )
A. n∈N,n2>2n+5 B. n∈N,n2≤2n+5
C. n∈N,n2≤2n+5 D. n∈N,n2=2n+5
4.设α∈R,则sinα-=( )
A.sin α B.-sin α C.cos α D.-cos α
5.已知a,b∈R,则“|a-b|<1”是“|a|+|b|<1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.已知向量a=(m,1),b=(2,-3),若a⊥b,则实数m=( )
A.- B. C. D.-
7.若数据x1,x2,…,xn的平均数为,方差为s2,则5x1+2,5x2+2,…,5xn+2的平均数和方差分别为( )
A.,s2 B.5+2,s2 C.5+2,25s2 D.,25s2
8.为得到函数y=sin 2x的图象,只需将函数y=sin2x-的图象( )
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D.向左平移个单位
9.科学研究已经证实,人的智力、情绪和体力分别以33天、28天和23天为周期,按y=sin(ωx+φ)进行变化,记智力曲线为I,情绪曲线为E,体力曲线为P,且现在三条曲线都处于x轴的同一点处,那么第322天时( )
A.智力曲线I处于最低点
B.情绪曲线E与体力曲线P都处于上升期
C.智力曲线I与情绪曲线E相交
D.情绪曲线E与体力曲线P都关于(322,0)对称
10.两条异面直线与同一平面所成的角,不可能是( )
A.两个角均为锐角 B.一个角为0°,一个角为90°
C.两个角均为0° D.两个角均为90°
11.已知定义在R上的函数f(x)满足:f(x)为奇函数,f(x+1)为偶函数,当0≤x≤1时,f(x)=2x-1,则f(log22 024)等于( )
A.- B. C.- D.
12.在三棱锥A-BCD中,平面ACD⊥平面BCD,△ACD是以CD为斜边的等腰直角三角形,AB⊥BC,AC=2CB=4,则该三棱锥的外接球的半径为( )
A.2 B.
C.2 D.
二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)
13.关于复数z=x+yi(x,y∈R,i为虚数单位),下列说法正确的是( )
A.z2=x2+y2 B.若|z-2i|=2,则x2+(y-2)2=4
C.若zi为纯虚数,则x≠0,y=0 D.|z|>(|x|+|y|)
14.已知函数f(x)=2x-2-x,函数g(x)=ln,则下列说法中正确的是( )
A.f(x)·g(x)是偶函数
B.f(x)·|g(x)|是奇函数
C.|f(x)|·g(x)是偶函数
D.|f(x)·g(x)|是偶函数
15.下列说法正确的是( )
A.若事件A,B互斥,则P(A∪B)=P(A)+P(B)
B.若事件A,B相互独立,则P()=P()P()
C.若事件A,B,C两两互斥,则P(A∪B∪C)=P(A)+P(B)+P(C)
D.若事件A,B,C两两独立,则P(ABC)=P(A)P(B)P(C)
16. 如图,正方体ABCD-A1B1C1D1的棱长为6,M,N分别为棱A1B1,BB1的中点,过D,M,N三点的平面截正方体,得到截面多边形α,则下列说法正确的是( )
A.多边形α是一个六边形
B.多边形α的周长为6+3
C.AC1⊥平面DMN
D.截面多边形α在顶点D处的内角的余弦值为
三、填空题(本大题共4小题,共15分)
17.已知函数f(x)=则f(sin 30°)= ,f(-3)= .
18.已知等腰三角形ABC的内角A,B,C的对边分别为a,b,c,且bsin B+(c-b)sin C=asin A,延长线段BC至D,使BD=5,若△ACD的面积S=,则AD= .
19.已知实数a>0,b>0,a-2b=1,则a2+4b2+的最小值为 .
20.已知2个单位向量m,n满足:对任意的x∈R,有|m+xn|≥恒成立.若2|c|=1,则对任意的λ∈R,|c-λm-(1-λ)n|的取值范围是 .
四、解答题(本大题共3小题,共33分)
21.(11分)某地为了了解市场经营户年收入情况,随机抽取60家经营户,经统计,这60家经营户去年经营收入(单位:万元)均在区间[4.5,10.5]内,按[4.5,5.5),[5.5,6.5),[6.5,7.5),[7.5,8.5),[8.5,9.5),[9.5,10.5]分成6组,频率分布直方图如图所示,若上述居民可支配收入数据的第80百分位数为8.9.
(1)求a,b的值;
(2)估计这60家经营户年收入的平均值(同一组中的数据用该区间的中点值作代表);
(3)用分层抽样的方法在收入区间为[6.5,8.5)的经营户中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1户在收入区间为[7.5,8.5)内的概率.
22.(11分)如图,在三棱锥P-ABC中,PA⊥AC,AB⊥BC,PA=6,AB=BC=8.设D,E,F分别为棱PC,AC,AB的中点,且DF=5.
(1)求证:平面DEF⊥平面ABC;
(2)求平面PBC与平面PAC所成角的正弦值.
23.(11分)已知函数f(x)=ax2-|x-a|,a∈R.
(1)当a=1时,求函数f(x)的单调递增区间(不必写明证明过程);
(2)判断函数f(x)的奇偶性,并说明理由;
(3)当-1≤a≤2时,若对任意的x∈[1,3],恒有f(x)+bx≤0成立,求a2+3b的最大值.
普通高中学业水平考试数学模拟卷(六)
1.D 解析 由题知A∪B={0,1,2}∪{0,2,4}={0,1,2,4},故选D.
2.A
3.B 解析 因为命题p: n∈N,n2>2n+5,
所以p的否定 p: n∈N,n2≤2n+5,故选B.
4.D 解析 sinα-=-sin-α=-cos α,故选D.
5.B
6.C 解析 ∵a=(m,1),b=(2,-3)且a⊥b,则a·b=2m-3=0,解得m=.
故选C.
7.C
8.D 解析 因为将函数y=sin2x-的图象向左平移个单位,则y=sin2x+-=sin 2x.
故选D.
9.D 解析 当第322天时,322除33余25,322除28余14,322除23余0,即智力曲线I位于周期处,情绪曲线E位于周期处,体力曲线P刚好位于起始点处,
A选项,因为,则智力曲线I不处于最低点,故A错误;
B选项,情绪曲线E处于最高点,即将开始下降,故B错误;
C选项,经过n个周期后,因为周期不同,所以智力曲线I与情绪曲线E不一定相交,故C错误;
D选项,(322,0)位于体力曲线P和情绪曲线E的交点x轴上,故D正确,故选D.
10.D 解析 对于A,两个角可能均为锐角,故A不符合题意;
对于B,可能一个角为0°,一个角为90°,故B不符合题意;
对于C,可能两个角均为0°,故C不符合题意;
对于D,如果两个角均为90°,则两条直线垂直于同一个平面,则这两条直线平行,不是异面直线,故这两个角不可能均为90°,故D符合题意.故选D.
11.A 解析 定义在R上的函数f(x)满足f(x)为奇函数,f(x+1)为偶函数,可得f(-x)=-f(x),f(-x+1)=f(x+1) f(-x)=f(x+2),则f(x+2)=-f(x),故f(x+4)=-f(x+2)=f(x),可得f(x)的最小正周期为4,
由于log22 024∈(10,11),则log22 024-12∈(-2,-1),(log22 024-12)+2∈(0,1),
当0≤x≤1时,f(x)=2x-1,
所以f(log22 024-12+2)=-1=2-10×-1=2 024×2-10-1=-1,
则f(log22 024)=f(log22 024-12)=-f(log22 024-10)=-(-1)=1-=1-=-.
故选A.
12. B 解析 设CD中点为M,连接AM,
因为△ACD是以CD为斜边的等腰直角三角形,AC=2CB=4,
所以AM=DM=CM=2,AM⊥CD,过点M作MN⊥CD,
因为平面ACD⊥平面BCD,平面ACD∩平面BCD=CD,MN 平面BCD,AM 平面ACD,
所以MN⊥平面ACD,AM⊥平面BCD,
所以三棱锥的外接球的球心在MN上,
设外接球的半径为R,
则由AB⊥BC得AB=2,
由AM⊥BM得BM=2=BC,
又因为BM2+BC2=CM2,
所以△BCM为等腰直角三角形,
设球心为O,CM中点为P,连接BP,
则MP=CP=BP=,
所以OM=-BP,
即,解得R=,故选B.
13.BC 解析 z2=(x+yi)2=x2+2xyi+y2i2=x2-y2+2xyi,故选项A错误;
|z-2i|=2,由几何意义可得(x,y)到(0,2)的距离为2,
进而可得,=2,即x2+(y-2)2=4,故选项B正确;
zi=(x+yi)i=-y+xi且为纯虚数,x≠0,y=0,故选项C正确;
|z|=,可取x=,y=,则|z|=(|x|+|y|)=×=,|z|=(|x|+|y|),选项D错误.
故选BC.
14.ABD 解析 函数f(x)=2x-2-x的定义域为R,函数g(x)=ln的定义域为(-1,1),f(-x)=2-x-2x=-f(x),g(-x)=ln=-ln=-g(x),
对于A,函数f(x)·g(x)的定义域为(-1,1),f(-x)·g(-x)=f(x)·g(x),f(x)·g(x)是偶函数,A正确;
对于B,函数f(x)·|g(x)|的定义域为(-1,1),f(-x)·|g(-x)|=-f(x)·|g(x)|,f(x)·|g(x)|是奇函数,B正确;
对于C,函数|f(x)|·g(x)的定义域为(-1,1),|f(-x)|·g(-x)=-|f(x)|·g(x),|f(x)|·g(x)是奇函数,C错误;
对于D,函数|f(x)·g(x)|的定义域为(-1,1),|f(-x)·g(-x)|=|f(x)·g(x)|,|f(x)·g(x)|是偶函数,D正确.
故选ABD.
15.ABC 解析 对于A,根据互斥事件的概率加法公式即可判断A正确;
对于B,若事件A,B相互独立,则也相互独立,所以P()=P()P(),故B正确;
对于C,根据互斥事件的概率加法公式即可判断C正确;
对于D,例如,从1,2,3,4中随机选出一个数字,记事件A=“取出的数字为1或2”,B=“取出的数字为1或3”,C=“取出的数字为1或4”,则AB=AC=BC=ABC=“取出的数字为1”,
显然P(A)=P(B)=P(C)=,
P(AB)=P(AC)=P(BC)=P(ABC)=,
满足P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C),
所以事件A,B,C两两独立,但是P(ABC)≠P(A)·P(B)P(C),故D错误.
故选ABC.
16. BD 解析 延长MN,AB相交于Q,连接DQ交BC于E,连接NE,
则由△BNQ≌△B1NM可得BQ=B1M=3,又△QBE∽△QAD,
∴ BE=2,
取B1H=2,连接D1H,过M作MF∥D1H,连接DF,
由于EH∥B1B,EH=B1B,
又DD1∥B1B,DD1=B1B,
∴EH∥D1D,EH=D1D,四边形DD1HE为平行四边形,故ED∥HD1,
又MF∥HD1,
∴MF∥ED,
根据,
∴NE∥DF,
则五边形MNEDF即为截面多边形,故A错误;
由MF∥D1H可知A1F=2,
∴五边形MNEDF的周长为MN+NE+ED+DF+MF=3=6+3,故B正确;
由于B1D1⊥A1C1,B1D1⊥A1A,且A1C1∩A1A=A1,A1C1,A1A 平面A1C1A,
∴B1D1⊥平面A1C1A,C1A 平面A1C1A,
∴C1A⊥D1B1,
若AC1⊥平面DMN,MF 平面DMN,则AC1⊥MF,MF∥D1H,故AC1⊥D1H,D1H∩D1B1=D1,D1H,D1B1 平面D1B1H,故AC1⊥平面D1B1H,这显然是不成立的,故AC1与平面DMN不垂直,故C错误;
连接EF,EH,HF,由于EH∥BB1,EH=BB1,HF∥A1B1,HF=A1B1,
∴四边形BEHB1,A1B1HF均为平行四边形,则EF==6,
cos∠EDF=,故D正确,故选BD.
17.-1 2 解析 因为f(x)=
则f(sin 30°)=f=log21-=-1,
f(-3)=log2(1+3)=2.
18. 解析 由正弦定理,b2+(c-b)c=a2,即bc=b2+c2-a2,
故cos A=,
又因为A∈(0,π),
故A=,
所以△ABC是等边三角形.
又因为△ACD的面积S=CA·CDsin∠ACD=,
故S=CA·(5-CA)·,
解得(CA-1)(CA-4)=0,
解得AC=1或AC=4.
当AC=1时,CD=5-1=4,当AC=4时,CD=5-4=1,
故AD2=CA2+CD2-2CA·CDcos=1+16+4=21,故AD=.
19.3 解析 实数a>0,b>0,a-2b=1,则a2+4b2+=(a-2b)2+4ab+≥1+2=3,
当且仅当b=,a=时,等号成立,
a2+4b2+的最小值为3.
20.,+∞ 解析 因为对任意的x∈R,有|m+xn|≥恒成立,所以(m+xn)2≥m-n2恒成立,
即m2+2xm·n+x2n2≥m2-m·n+n2恒成立,
又因为m,n为单位向量,所以x2+2xm·n+m·n-≥0恒成立,
所以Δ=(2m·n)2-4m·n-=4(m·n)2-4m·n+1=(2m·n-1)2≤0,
所以2m·n-1=0,所以m·n=,设m与n的夹角为θ,则m·n=|m||n|cos θ=cos θ=,
又因为θ∈[0,π],所以θ=,不妨设m==(1,0),n==,c==(x,y),
因为2|c|=1,所以x2+y2=,所以点C在以坐标原点为圆心,半径r=的圆上,
设=λm+(1-λ)n=λ+(1-λ),
则D在直线AB上,
又因为直线AB的方程为y=(x-1),
即x+y-=0,
所以c-λm-(1-λ)n=,
所以|c-λm-(1-λ)n|=||,
又因为O到直线AB的距离d=,
所以||≥-r=,
即|c-λm-(1-λ)n|的取值范围是,+∞.
21.解 (1)依题意得0.10+0.15+0.15+a+b+0.05=1,
即a+b=0.55,
又第80百分位数在[8.5,9.5),
∴0.05+0.6b=1-0.8,解得a=0.3,b=0.25.
(2)=5×0.1+6×0.15+7×0.15+8×0.3+9×0.25+10×0.05=7.6.
(3)在[6.5,7.5)有9户,在[7.5,8.5)有18户,
所以在[6.5,7.5)内抽取2户,在[7.5,8.5)内抽取4户,
设在[6.5,7.5)内抽取的2户为A1,A2,在[7.5,8.5)内抽取的4户为B1,B2,B3,B4,
任取2户的所有情况为A1A2,A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4,B1B2,B1B3,B1B4,B2B3,B2B4,B3B4,共15种情况,
其中至多有1户在[7.5,8.5)内的样本点包含A1A2,A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4,共9个,
设至多有1户在[7.5,8.5)内为事件A,则P(A)=.
22.(1)证明 由PA⊥AC,D,E分别为棱PC,AC的中点,得DE∥PA,DE⊥AC,
AB=BC=8,D,E,F分别为棱PC,AC,AB的中点,且EF=4,DE=3,DF=5,
DF2=DE2+EF2,DE⊥EF,EF 平面ABC,AC 平面ABC,EF∩AC=E,
∴DE⊥平面ABC,DE 平面DEF.
∴平面DEF⊥平面ABC.
(2)解 连接BE,则由AB=BC,BE⊥AC,得DE⊥BE,DE∩AC=E,DE 平面ABC,AC 平面ABC,
∴DE⊥平面ABC,
过点B作BH⊥PC,垂足为H,连接EH,
则∠EHB是二面角B-PC-A的平面角.
于是PB=10,BC=8,PC=2,
∴BH=,
∵AB=BC=8,AC=8,
∴BE=4,
∴sin∠EHB=.
23.解 (1)当a=1时,f(x)=x2-|x-1|=
由二次函数的性质可知,当x≥1时,f(x)=x2-x+1,此时f(x)在[1,+∞)内单调递增,当x<1时,f(x)=x2+x-1,f(x)在-,1内单调递增,
故f(x)的单调递增区间为-,+∞.
(2)当a=0时,f(x)=-|x|,对于 x∈R,f(-x)=-|x|=f(x),
故f(x)为偶函数,
当a≠0时,f(0)=-|a|≠0,故f(x)不是奇函数,
又f(1)=a-|1-a|,f(-1)=a-|1+a|,显然|1-a|≠|1+a|,
即f(1)≠f(-1),故f(x)不是偶函数,
综上所述,当a=0时,f(x)是偶函数,当a≠0时,f(x)既不是偶函数又不是奇函数.
(3)①当-1≤a≤1时,“f(x)+bx≤0在[1,3]上恒成立”等价于“ax2+(b-1)x+a≤0在[1,3]上恒成立”,也就是b≤-ax++1恒成立,
由于y=x+在[1,3]上单调递增,
若0≤a≤1,则y=-ax++1在[1,3]上单调递减,
故当x=3时,y=-ax++1取最小值,
则-ax++1min=1-a,所以b≤1-a,
故a2+3b≤a2-10a+3≤3;
若-1≤a<0,则y=-ax++1在[1,3]上单调递增,-ax++1min=1-2a,
所以b≤1-2a,
于是a2+3b≤a2-6a+3≤10,当a=-1,b=3时,等号成立.
②当1
所以y=-ax--1在[1,3]上单调递减,
当1
综上所述,a2+3b的最大值为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
