2024数学学业水平考试专题练--专题2 三角函数与解三角形的综合应用(含解析)
文档属性
| 名称 | 2024数学学业水平考试专题练--专题2 三角函数与解三角形的综合应用(含解析) | 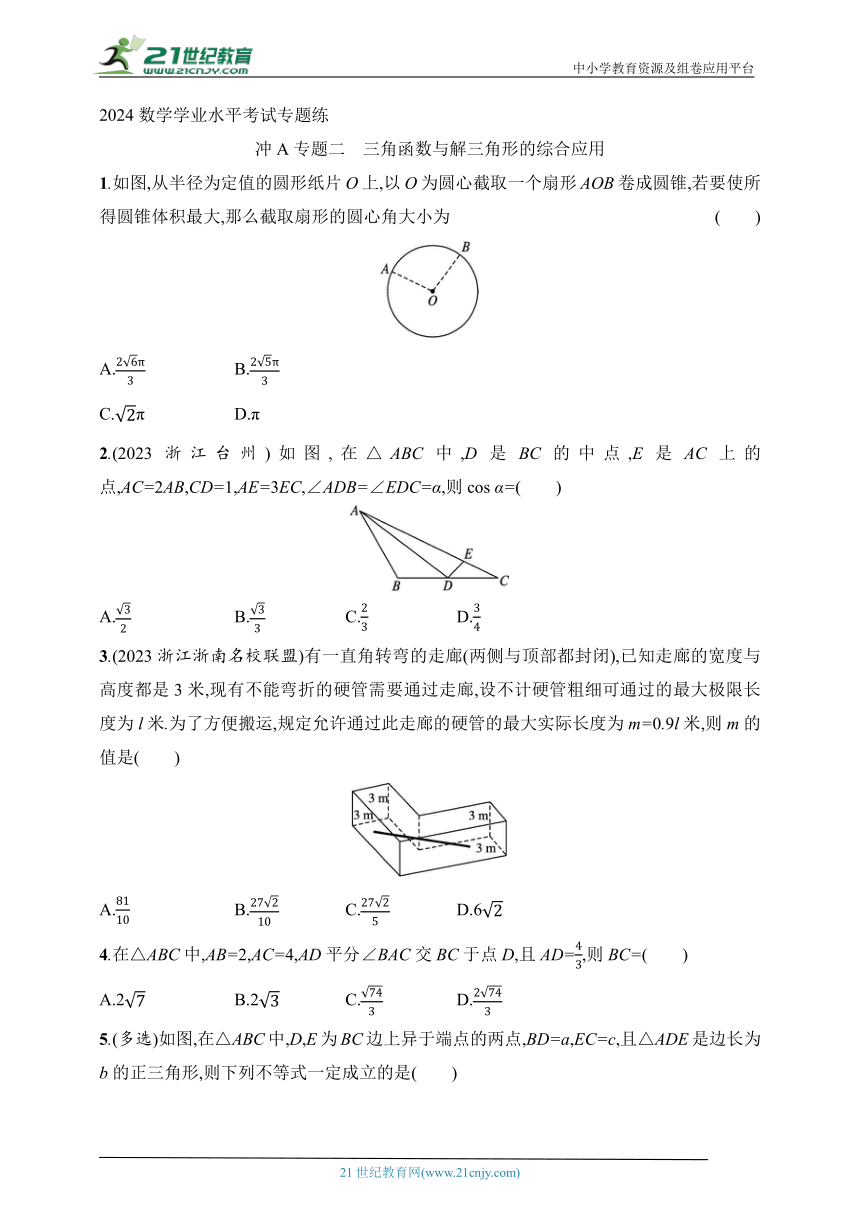 | |
| 格式 | docx | ||
| 文件大小 | 428.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:30:19 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
2024数学学业水平考试专题练
冲A专题二 三角函数与解三角形的综合应用
1.如图,从半径为定值的圆形纸片O上,以O为圆心截取一个扇形AOB卷成圆锥,若要使所得圆锥体积最大,那么截取扇形的圆心角大小为 ( )
A. B.
C.π D.π
2.(2023浙江台州)如图,在△ABC中,D是BC的中点,E是AC上的点,AC=2AB,CD=1,AE=3EC,∠ADB=∠EDC=α,则cos α=( )
A. B. C. D.
3.(2023浙江浙南名校联盟)有一直角转弯的走廊(两侧与顶部都封闭),已知走廊的宽度与高度都是3米,现有不能弯折的硬管需要通过走廊,设不计硬管粗细可通过的最大极限长度为l米.为了方便搬运,规定允许通过此走廊的硬管的最大实际长度为m=0.9l米,则m的值是( )
A. B. C. D.6
4.在△ABC中,AB=2,AC=4,AD平分∠BAC交BC于点D,且AD=,则BC=( )
A.2 B.2 C. D.
5.(多选)如图,在△ABC中,D,E为BC边上异于端点的两点,BD=a,EC=c,且△ADE是边长为b的正三角形,则下列不等式一定成立的是( )
A.>a+b+c
B.>a+b+c
C.D.6.(多选)(2023浙江学考)在锐角三角形ABC中,有 ( )
A.sin A+sin B>sin C
B.sin2A+sin2B>sin2C
C.cos A+cos B>sin C
D.cos2A+cos2B>sin2C
7.(2023浙江学考)已知△ABC的三个角A,B,C所对的边为a,b,c,若∠BAC=,D为边BC上一点,且AD=2,BD∶DC=4c∶b,则的值为 .
8.已知x,y∈R,且x2-2xy+2y2=1,则x+2y的最大值为 ,x2+y2的取值范围是 .
9.(2023浙江绍兴)如图,在平面四边形ABCD中,点B与点D分别在直线AC的两侧,BC=CD=2.
(1)已知AB=2,且AC=AD,
①当cos∠CAD=时,求△ABC的面积;
②若∠ABC=2∠ADC>,求∠ABC.
(2)已知AD=AB,且∠BAD=,求AC的最大值.
10.(2023浙江温州知临中学)某市决定充分利用城市空间修建口袋儿童乐园,如图所示,在直径为20 m的半圆O空地上,设置扇形区域OMB作为大人休息区,规划两个三角形区域做成小喷泉区(△OAB区域)和沙坑滑梯区(△ABC区域),其中A为直径MN延长线上一点,且OA=20 m,B为半圆周上一动点,以AB为边作等边三角形ABC.
(1)若等边三角形ABC的边长为a,∠AMB=θ,试写出a关于θ的函数关系式.
(2)问当∠AMB为多少时,儿童游玩区OACB的面积最大 这个最大面积为多少
11.(2023浙江温州新力量联盟)已知a,b,c分别是△ABC三个内角A,B,C的对边,且2bcosA-=c.
(1)求角B的大小;
(2)若b=,求△ABC面积的最大值;
(3)若b2=ac,且△ABC的外接圆半径为2,圆心为O,P为☉O上的一动点,试求的取值范围.
12.(2023浙江浙南名校联盟)在△ABC中,已知B=,AC=2,BD为边AC上的高.设y=BD+DC,记y关于A的函数为y=f(A).
(1)求y=f(A)的表达式及f(A)的取值范围;
(2)若不等式mf(A)+m≥f2(A)恒成立,求实数m的取值范围.
冲A专题二 三角函数与解三角形的综合应用
1.A 解析 设扇形AOB的半径为R,扇形的圆心角为θ(0<θ<2π),则扇形的弧长为θR,设圆锥的底面半径为r,高为h,则2πr=θR,则r=,则h==R,所以该圆锥的体积为V=πr2h=π×2×RπR3,当且仅当4π2-θ2=时,即当θ=π时,等号成立.故选A.
2.D 解析 由点D是BC的中点,AC=2AB,CD=1,AE=3EC,设CE=x,则BD=1,AE=3x,AB=2x,在△ABC中,可得,即sin B=2sin C,在△ABD中,可得,在△CED中,可得,上面两式相除可得2=,即AD=4DE.在△ABD中,4x2=1+AD2-2ADcos α=1+16DE2-8DEcos α,在△CDE中,x2=1+DE2-2DEcos α,即有4+4DE2=1+16DE2,解得DE=,AD=2,则x2=1+-2×cos α=-cos α.在△ADE中,9x2=AD2+DE2-2AD·DE·cos(π-2α)=4++2×2×cos 2α=+2cos 2α=4cos2α+,可得-9cos α=4cos2α+,化为4cos2α+9cos α-9=0,解得cos α=(cos α=-3舍去).故选D.
3.A 解析 如图所示,先求出硬管不倾斜,水平方向通过的最大长度AB,
设∠BAQ=θ0<θ<,则∠ABQ=-θ,
过点A作AC垂直内侧墙壁于点C,过点B作BD垂直内侧墙壁于点D,则AC=BD=3,∠CPA=∠BAQ=θ,∠DPB=∠ABQ=-θ,
在直角三角形ACP中,sin∠CPA=sin θ=,
所以AP=,
同理BP=,
所以AB=AP+BP=0<θ<.
因为AB=≥3×2=6≥6当且仅当sin θ=cos θ且θ=时,等号成立,
所以AB≥6.
因为走廊的宽度与高度都是3米,所以把硬管倾斜后能通过的最大长度为l==9,
所以m=0.9l=0.9×9=.故选A.
4.
A 解析 如图所示,在△ABC中,AB=2,AC=4,AD平分∠BAC交BC于点D,且AD=,设∠BAD=∠CAD=θ,可得S△ABD=×2×sin θ,S△ACD=×4×sin θ,且S△ABC=×2×4sin 2θ,因为S△ABD+S△ACD=S△ABC,可得sin θ=sin 2θ,即sin θ=2sin θcos θ,因为θ∈0,,所以sin θ>0,可得cos θ=,所以θ=,BC2=22+42-2×2×4cos=28,所以BC=2.故选A.
5.BC 解析 由题知∠ADB=∠AEC=120°,AB=,同理AC=,根据三角形三边关系AB+AC>BC可知,B选项正确;由AB-AC0,而a-b+c=-1<0,D选项错误.故选BC.
6.ABC 解析 对于A,根据正弦定理,因为a+b>c可得sin A+sin B>sin C,故A正确;对于B,因为cos C=>0可得a2+b2>c2,由正弦定理可得sin2A+sin2B>sin2C,故B正确;对于C,因为0cos Asin B+cos Bsin A=sin(A+B)=sin C,故C正确;对于D,当A=B=C=时,cos2A+cos2B==sin2C,故D错误.故选ABC.
7. 解析 设∠BAD=θ0<θ<,则∠CAD=-θ,
∵AD=2,BD∶DC=4c∶b,
∴,
即,
化简得2cos θ=sin θ,即tan θ=,
故sin θ=,sin-θ=sin θ=,
又S△ABC=S△ABD+S△ACD,
∴bcsin×2csin θ+×2bsin-θ,
即.
8. 解析 由题意可知(x-y)2+y2=1,令∴x+2y=cos θ+3sin θ=sin(θ+φ),其中tan φ=,
∴x+2y的最大值为;x2+y2=1+sin 2θ+(1-cos 2θ)=sin(2θ-α),其中tan α=,
∴x2+y2的取值范围是.
9.解 (1)①设AC=2x(0∵cos B=,∴sin B=,
S△ABC=×2×2×.
②设∠ADC=α>,取AC,CD的中点分别为M,N,连接BM,AN,BM⊥AC,AN⊥CD,AD=,AC=2AM=4sin α,
因为AC=AD,
所以=4sin α,
即sin 2α=,解得2α=,即∠ABC=.
(2)作CO⊥BD于O(图略),由余弦定理得AB=BD,∠ABD=,设∠CBO=θ,则BO=2cos θ,AB=BD=4cos θ,
在△ABC中,利用余弦定理得AC2=AB2+BC2-2AB·BC·cos∠ABC=16cos2θ+4-2×4cos θ×2×cos+θ=8sin2θ++12≤12+8,
则AC的最大值是2+2.
10.解 (1)∵∠AMB=θ,∴∠AOB=2θ.
在△AOB中,AB=a,OA=20,OB=10,∠AOB=2θ,
由余弦定理可得a2=OA2+OB2-2OA·OBcos∠AOB=500-400cos 2θ,
所以a=10,其中θ∈0,.
(2)S△AOB=×10×20sin 2θ=100sin 2θ,S△ABC=AB2=25(5-4cos 2θ),
所以S四边形OACB=S△AOB+S△ABC=100sin 2θ+25(5-4cos 2θ)=100sin 2θ-100cos 2θ+125=200sin2θ-+125.
因为0<θ<,则-<2θ-,
当2θ-,即θ=时,四边形OACB的面积取最大值(200+125)m2.
11.解 (1)由2bcosA-=c及正弦定理可得2sin B·cosA-=sin C,
又A+B+C=π,∴2sin Bcos Acos+sin Asin=sin[π-(A+B)],
整理可得cos Asin B+sin Asin B=sin(A+B),可得cos Asin B+sin Asin B=sin Acos B+cos Asin B,
可得sin Asin B=sin Acos B,
∵sin A≠0,∴tan B=.
∵B∈(0,π),∴B=.
(2)若b=,根据余弦定理得a2+c2-2ac·cos=6,
化简a2+c2-ac=6,
又a2+c2-ac≥2ac-ac=ac,
∴ac≤6,当且仅当a=c时,ac有最大值6.
∵△ABC的面积S=ac·sin B=ac≤×6=,
∴当且仅当a=c时,△ABC面积有最大值,最大值为.
(3)由正弦定理=2R,则b=2,则ac=b2=12,
由a2+c2=b2+ac,可得a2+c2=24,则a=c=2,
则三角形ABC为等边三角形,取AB中点M,如图所示,
则=()·()=·()+-3,
由OP=2,OM=1,则PM∈[1,3],则∈[-2,6].
12.解 (1)由已知可得AB=2cos A,BC=2sin A,
∵BD⊥AC,∴BD=AB·sin A=2cos Asin A,DC=BC·sin∠CBD=BC·sin A=2sin2A,
∴f(A)=BD+DC=2cos Asin A+2sin2A=sin 2A+1-cos 2A=sin2A-+1.
∵0∴sin2A-∈-,1,∴0即f(A)的取值范围为(0,+1].
(2)由(1)知f(A)+1>0,∴m≥.
记u=f(A)+1∈(1,2+],则设t==u+-2,
设u1,u2∈(1,2+],且u1∵u1,u2∈(1,2+],∴u1u2>1,u1u2-1>0.
∵u1即t=u+-2在(1,2+]上单调递增.
∴当u=2+,即f(A)+1=2+,f(A)=1+,A=时,t取到最大值为1+.
∴m≥1+,即实数m的取值范围为1+,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024数学学业水平考试专题练
冲A专题二 三角函数与解三角形的综合应用
1.如图,从半径为定值的圆形纸片O上,以O为圆心截取一个扇形AOB卷成圆锥,若要使所得圆锥体积最大,那么截取扇形的圆心角大小为 ( )
A. B.
C.π D.π
2.(2023浙江台州)如图,在△ABC中,D是BC的中点,E是AC上的点,AC=2AB,CD=1,AE=3EC,∠ADB=∠EDC=α,则cos α=( )
A. B. C. D.
3.(2023浙江浙南名校联盟)有一直角转弯的走廊(两侧与顶部都封闭),已知走廊的宽度与高度都是3米,现有不能弯折的硬管需要通过走廊,设不计硬管粗细可通过的最大极限长度为l米.为了方便搬运,规定允许通过此走廊的硬管的最大实际长度为m=0.9l米,则m的值是( )
A. B. C. D.6
4.在△ABC中,AB=2,AC=4,AD平分∠BAC交BC于点D,且AD=,则BC=( )
A.2 B.2 C. D.
5.(多选)如图,在△ABC中,D,E为BC边上异于端点的两点,BD=a,EC=c,且△ADE是边长为b的正三角形,则下列不等式一定成立的是( )
A.>a+b+c
B.>a+b+c
C.
A.sin A+sin B>sin C
B.sin2A+sin2B>sin2C
C.cos A+cos B>sin C
D.cos2A+cos2B>sin2C
7.(2023浙江学考)已知△ABC的三个角A,B,C所对的边为a,b,c,若∠BAC=,D为边BC上一点,且AD=2,BD∶DC=4c∶b,则的值为 .
8.已知x,y∈R,且x2-2xy+2y2=1,则x+2y的最大值为 ,x2+y2的取值范围是 .
9.(2023浙江绍兴)如图,在平面四边形ABCD中,点B与点D分别在直线AC的两侧,BC=CD=2.
(1)已知AB=2,且AC=AD,
①当cos∠CAD=时,求△ABC的面积;
②若∠ABC=2∠ADC>,求∠ABC.
(2)已知AD=AB,且∠BAD=,求AC的最大值.
10.(2023浙江温州知临中学)某市决定充分利用城市空间修建口袋儿童乐园,如图所示,在直径为20 m的半圆O空地上,设置扇形区域OMB作为大人休息区,规划两个三角形区域做成小喷泉区(△OAB区域)和沙坑滑梯区(△ABC区域),其中A为直径MN延长线上一点,且OA=20 m,B为半圆周上一动点,以AB为边作等边三角形ABC.
(1)若等边三角形ABC的边长为a,∠AMB=θ,试写出a关于θ的函数关系式.
(2)问当∠AMB为多少时,儿童游玩区OACB的面积最大 这个最大面积为多少
11.(2023浙江温州新力量联盟)已知a,b,c分别是△ABC三个内角A,B,C的对边,且2bcosA-=c.
(1)求角B的大小;
(2)若b=,求△ABC面积的最大值;
(3)若b2=ac,且△ABC的外接圆半径为2,圆心为O,P为☉O上的一动点,试求的取值范围.
12.(2023浙江浙南名校联盟)在△ABC中,已知B=,AC=2,BD为边AC上的高.设y=BD+DC,记y关于A的函数为y=f(A).
(1)求y=f(A)的表达式及f(A)的取值范围;
(2)若不等式mf(A)+m≥f2(A)恒成立,求实数m的取值范围.
冲A专题二 三角函数与解三角形的综合应用
1.A 解析 设扇形AOB的半径为R,扇形的圆心角为θ(0<θ<2π),则扇形的弧长为θR,设圆锥的底面半径为r,高为h,则2πr=θR,则r=,则h==R,所以该圆锥的体积为V=πr2h=π×2×RπR3,当且仅当4π2-θ2=时,即当θ=π时,等号成立.故选A.
2.D 解析 由点D是BC的中点,AC=2AB,CD=1,AE=3EC,设CE=x,则BD=1,AE=3x,AB=2x,在△ABC中,可得,即sin B=2sin C,在△ABD中,可得,在△CED中,可得,上面两式相除可得2=,即AD=4DE.在△ABD中,4x2=1+AD2-2ADcos α=1+16DE2-8DEcos α,在△CDE中,x2=1+DE2-2DEcos α,即有4+4DE2=1+16DE2,解得DE=,AD=2,则x2=1+-2×cos α=-cos α.在△ADE中,9x2=AD2+DE2-2AD·DE·cos(π-2α)=4++2×2×cos 2α=+2cos 2α=4cos2α+,可得-9cos α=4cos2α+,化为4cos2α+9cos α-9=0,解得cos α=(cos α=-3舍去).故选D.
3.A 解析 如图所示,先求出硬管不倾斜,水平方向通过的最大长度AB,
设∠BAQ=θ0<θ<,则∠ABQ=-θ,
过点A作AC垂直内侧墙壁于点C,过点B作BD垂直内侧墙壁于点D,则AC=BD=3,∠CPA=∠BAQ=θ,∠DPB=∠ABQ=-θ,
在直角三角形ACP中,sin∠CPA=sin θ=,
所以AP=,
同理BP=,
所以AB=AP+BP=0<θ<.
因为AB=≥3×2=6≥6当且仅当sin θ=cos θ且θ=时,等号成立,
所以AB≥6.
因为走廊的宽度与高度都是3米,所以把硬管倾斜后能通过的最大长度为l==9,
所以m=0.9l=0.9×9=.故选A.
4.
A 解析 如图所示,在△ABC中,AB=2,AC=4,AD平分∠BAC交BC于点D,且AD=,设∠BAD=∠CAD=θ,可得S△ABD=×2×sin θ,S△ACD=×4×sin θ,且S△ABC=×2×4sin 2θ,因为S△ABD+S△ACD=S△ABC,可得sin θ=sin 2θ,即sin θ=2sin θcos θ,因为θ∈0,,所以sin θ>0,可得cos θ=,所以θ=,BC2=22+42-2×2×4cos=28,所以BC=2.故选A.
5.BC 解析 由题知∠ADB=∠AEC=120°,AB=,同理AC=,根据三角形三边关系AB+AC>BC可知,B选项正确;由AB-AC
6.ABC 解析 对于A,根据正弦定理,因为a+b>c可得sin A+sin B>sin C,故A正确;对于B,因为cos C=>0可得a2+b2>c2,由正弦定理可得sin2A+sin2B>sin2C,故B正确;对于C,因为0
7. 解析 设∠BAD=θ0<θ<,则∠CAD=-θ,
∵AD=2,BD∶DC=4c∶b,
∴,
即,
化简得2cos θ=sin θ,即tan θ=,
故sin θ=,sin-θ=sin θ=,
又S△ABC=S△ABD+S△ACD,
∴bcsin×2csin θ+×2bsin-θ,
即.
8. 解析 由题意可知(x-y)2+y2=1,令∴x+2y=cos θ+3sin θ=sin(θ+φ),其中tan φ=,
∴x+2y的最大值为;x2+y2=1+sin 2θ+(1-cos 2θ)=sin(2θ-α),其中tan α=,
∴x2+y2的取值范围是.
9.解 (1)①设AC=2x(0
S△ABC=×2×2×.
②设∠ADC=α>,取AC,CD的中点分别为M,N,连接BM,AN,BM⊥AC,AN⊥CD,AD=,AC=2AM=4sin α,
因为AC=AD,
所以=4sin α,
即sin 2α=,解得2α=,即∠ABC=.
(2)作CO⊥BD于O(图略),由余弦定理得AB=BD,∠ABD=,设∠CBO=θ,则BO=2cos θ,AB=BD=4cos θ,
在△ABC中,利用余弦定理得AC2=AB2+BC2-2AB·BC·cos∠ABC=16cos2θ+4-2×4cos θ×2×cos+θ=8sin2θ++12≤12+8,
则AC的最大值是2+2.
10.解 (1)∵∠AMB=θ,∴∠AOB=2θ.
在△AOB中,AB=a,OA=20,OB=10,∠AOB=2θ,
由余弦定理可得a2=OA2+OB2-2OA·OBcos∠AOB=500-400cos 2θ,
所以a=10,其中θ∈0,.
(2)S△AOB=×10×20sin 2θ=100sin 2θ,S△ABC=AB2=25(5-4cos 2θ),
所以S四边形OACB=S△AOB+S△ABC=100sin 2θ+25(5-4cos 2θ)=100sin 2θ-100cos 2θ+125=200sin2θ-+125.
因为0<θ<,则-<2θ-,
当2θ-,即θ=时,四边形OACB的面积取最大值(200+125)m2.
11.解 (1)由2bcosA-=c及正弦定理可得2sin B·cosA-=sin C,
又A+B+C=π,∴2sin Bcos Acos+sin Asin=sin[π-(A+B)],
整理可得cos Asin B+sin Asin B=sin(A+B),可得cos Asin B+sin Asin B=sin Acos B+cos Asin B,
可得sin Asin B=sin Acos B,
∵sin A≠0,∴tan B=.
∵B∈(0,π),∴B=.
(2)若b=,根据余弦定理得a2+c2-2ac·cos=6,
化简a2+c2-ac=6,
又a2+c2-ac≥2ac-ac=ac,
∴ac≤6,当且仅当a=c时,ac有最大值6.
∵△ABC的面积S=ac·sin B=ac≤×6=,
∴当且仅当a=c时,△ABC面积有最大值,最大值为.
(3)由正弦定理=2R,则b=2,则ac=b2=12,
由a2+c2=b2+ac,可得a2+c2=24,则a=c=2,
则三角形ABC为等边三角形,取AB中点M,如图所示,
则=()·()=·()+-3,
由OP=2,OM=1,则PM∈[1,3],则∈[-2,6].
12.解 (1)由已知可得AB=2cos A,BC=2sin A,
∵BD⊥AC,∴BD=AB·sin A=2cos Asin A,DC=BC·sin∠CBD=BC·sin A=2sin2A,
∴f(A)=BD+DC=2cos Asin A+2sin2A=sin 2A+1-cos 2A=sin2A-+1.
∵0
(2)由(1)知f(A)+1>0,∴m≥.
记u=f(A)+1∈(1,2+],则设t==u+-2,
设u1,u2∈(1,2+],且u1
∵u1
∴当u=2+,即f(A)+1=2+,f(A)=1+,A=时,t取到最大值为1+.
∴m≥1+,即实数m的取值范围为1+,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
