2024数学学业水平考试专题练--优化集训6 指数与指数函数(含解析)
文档属性
| 名称 | 2024数学学业水平考试专题练--优化集训6 指数与指数函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:39:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024数学学业水平考试专题练
优化集训6 指数与指数函数
基础巩固
1.函数f(x)=ab-x的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0
C.00
2.已知=5,那么等于( )
A. B.- C.± D.7
3.化简(a>0,b>0)的结果为( )
A. B.ab C. D.
4.若函数f(x)=有最大值3,则实数a的值为( )
A.-2 B.-1
C.1 D.2
5.已知a=0.20.3,b=0.20.5,c=0.30.3,则以下关系不正确的是( )
A.bC. D.
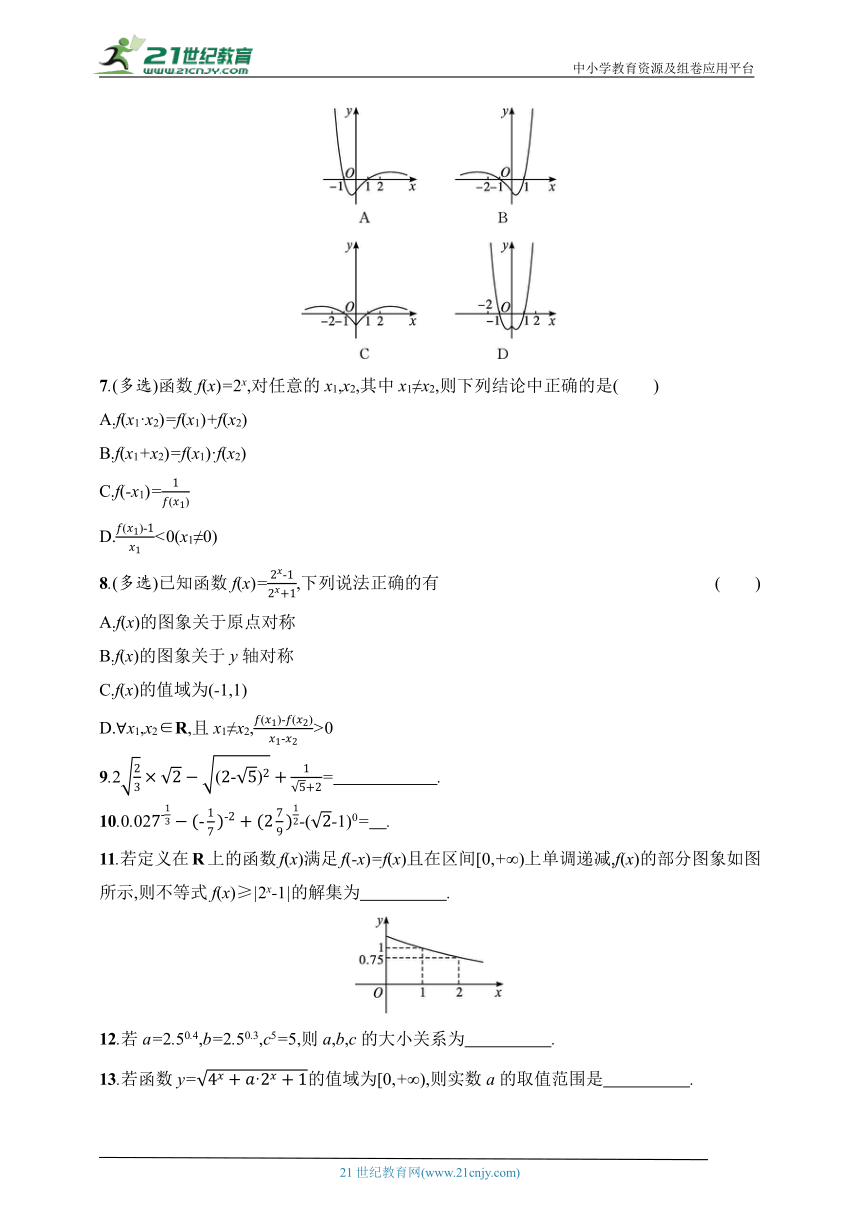
6.函数f(x)=的图象大致为( )
7.(多选)函数f(x)=2x,对任意的x1,x2,其中x1≠x2,则下列结论中正确的是( )
A.f(x1·x2)=f(x1)+f(x2)
B.f(x1+x2)=f(x1)·f(x2)
C.f(-x1)=
D.<0(x1≠0)
8.(多选)已知函数f(x)=,下列说法正确的有 ( )
A.f(x)的图象关于原点对称
B.f(x)的图象关于y轴对称
C.f(x)的值域为(-1,1)
D. x1,x2∈R,且x1≠x2,>0
9.2= .
10.0.02-(-1)0= .
11.若定义在R上的函数f(x)满足f(-x)=f(x)且在区间[0,+∞)上单调递减,f(x)的部分图象如图所示,则不等式f(x)≥|2x-1|的解集为 .
12.若a=2.50.4,b=2.50.3,c5=5,则a,b,c的大小关系为 .
13.若函数y=的值域为[0,+∞),则实数a的取值范围是 .
14.若f(x)=是R上的增函数,则实数a的取值范围为 .
15.若直线y=2a与函数y=|ax-1|(a>0,a≠1)的图象有两个公共点,则a的取值范围是 .
16.已知函数f(x)=4x+a·2x+3,a∈R.
(1)当a=-4时,x∈[0,2],求函数f(x)的值域;
(2)若对任意的x∈(0,+∞),f(x)>0恒成立,求实数a的取值范围.
17.已知函数f(x)=2x+k·2-x,k∈R.
(1)若函数f(x)为奇函数,求实数k的值;
(2)若对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.
能力提升
18.(多选)关于函数f(x)=,下列结论中正确的是( )
A.当a=0时,f(x)是增函数
B.当a=0时,f(x)的值域为(-1,+∞)
C.当a=1时,f(x)是奇函数
D.若f(x)的定义域为R,则a<2
19.(多选)已知a,b分别是方程2x+x=0,3x+x=0的两个实数根,则下列选项中正确的是( )
A.-1C.b·3a20.函数f(x)为定义域在R上的偶函数,当x≥0时,f(x)=-x-,则满足f(x-2)≤-1的x的取值范围是 .
21.已知a>0,函数f(x)=,x∈[-a,a]的最大值、最小值分别为M,N,则M+N= .
22.设函数f(x)=则满足f(x)+f(x-)>1的x的取值范围是 .
23.(2023浙江温州)已知函数f(x)=为偶函数.
(1)求出a的值,并写出单调区间;
(2)若存在x∈[0,1]使得不等式bf(2x)+1≥f(x)成立,求实数b的取值范围.
优化集训6 指数与指数函数
基础巩固
1.A
2.C 解析 当x>0时,>0,>0,此时>0;当x<0时,<0,<0,此时<0.
∵+2=5+2=7,
∴=±.故选C.
3.A 解析 原式==ab-1.故选A.
4.D 解析 由于函数f(x)=有最大值3,所以a>0,且当x=-时,f(x)取得最大值为f==3,故-1=1,=2,a=2.故选D.
5.D 解析 ∵指数函数y=0.2x为减函数,∴0.20.3>0.20.5,即a>b,∵幂函数y=x0.3是增函数,∴0.30.3>0.20.3,即c>a,a,b,c的大小关系为00,∴ab0,∴bc6.A 解析 函数f(x)为非奇非偶函数,关于y轴不对称,排除C,D,当x→+∞时,f(x)→0,排除B,故选A.
7.BC
8.ACD 解析 f(x)=的定义域为R,关于原点对称,f(-x)==-f(x),所以f(x)是奇函数,图象关于原点对称,故选项A正确,选项B不正确;f(x)==1-,因为2x>0,所以2x+1>1,所以0<<1,-2<<0,所以-1<1-<1,可得f(x)的值域为(-1,1),故选项C正确;设任意的x10,+1>0,<0,所以<0,即f(x1)-f(x2)<0,所以>0,故选项D正确.故选ACD.
9. 解析 2=2×-(-2)++2+-2=.
10.-45 解析 0.02-(-1)0=-49+-1=-49+-1=-45.
11.[-2,1] 解析 由图可知f(-2)=f(2)=0.75,f(1)=1,
所以f(x)≥|2x-1|的解集为[-2,1].
12.b0),则f(x)在(0,+∞)上单调递增,所以a>c>b.
13.(-∞,-2] 解析 设g(x)=4x+a·2x+1,若函数y=的值域为[0,+∞),则等价于[0,+∞)是g(x)值域的子集,y=g(x)=4x+a·2x+1=(2x)2+a·2x+1,设t=2x,则t>0,则y=h(t)=t2+at+1.∵h(0)=1>0,∴当图象的对称轴t=-≤0,即a≥0时,不满足条件.当t=->0,即a<0时,判别式Δ=a2-4≥0,即则a≤-2,即实数a的取值范围是(-∞,-2].
14.[4,8) 解析 ∵当x>1时,f(x)=ax单调递增,∴a>1,
∵一次函数在(-∞,1]上单调递增,∴4->0,a<8,
且当x=1时应有(4-)×1+2≤a1,解得a≥4.
综上可得,实数a的取值范围是[4,8).
15.(0,) 解析 当00,a≠1)的图象有两个公共点时,0<2a<1,01时,得无解.综上,a的取值范围为(0,).
16.解 (1)当a=-4时,令t=2x,由x∈[0,2],得t∈[1,4],
y=t2-4t+3=(t-2)2-1,
当t=2时,ymin=-1;
当t=4时,ymax=3.
∴函数f(x)的值域为[-1,3].
(2)设t=2x,则t>1,f(x)>0对任意的x∈(0,+∞)恒成立,等价于t2+at+3>0对任意的t∈(1,+∞)恒成立,
∴a>-(t+)在(1,+∞)内恒成立,
∴a>.
设g(t)=-( t+),t>1,函数g(t)在(1,)内单调递增,在(,+∞)上单调递减,
∴g(t)max=g()=-2,
∴a>-2,即a的取值范围为(-2,+∞).
17.解 (1)因为f(x)=2x+k·2-x,k∈R是奇函数,
所以f(-x)=-f(x),x∈R,
即2-x+k·2x=-(2x+k·2-x),
所以k=-1.
(2)因为对任意的x∈[0,+∞),均有f(x)>2-x,
即2x+k·2-x>2-x成立,
所以1-k<22x对x≥0恒成立,所以1-k<.
因为y=22x在[0,+∞)上单调递增,所以(22x)min=1,
所以k>0,即k的取值范围为(0,+∞).
能力提升
18.ACD 解析 当a=0时,f(x)==1-,u=4x+1,由函数u=4x+1单调递增,知函数y=1-在(0,+∞)上单调递增,所以f(x)=1-在R上单调递增,A符合题意;因为4x+1>1,0<<1,-2<-<0,所以f(x)==1-∈(-1,1),B不符合题意;当a=1时,f(x)=定义域为R,而f(-x)==-f(x),所以f(x)是奇函数,C符合题意;若f(x)的定义域为R,则4x+1-a·2x≠0恒成立,即a≠,因为=2x+≥2,当且仅当2x=,即x=0时,等号成立,所以a<2,D符合题意.故选ACD.
19.BD 解析 函数y=2x,y=3x,y=-x在同一坐标系中的图象如下,
所以-1a·3b.
20.(-∞,1]∪[3,+∞) 解析 当x≥0时,函数f(x)=-x-是减函数,且f(1)=-1,∴不等式f(x-2)≤-1 f(x-2)≤f(1),又函数是偶函数,∴|x-2|≥1,故x的取值范围是(-∞,1]∪[3,+∞).
21.4 047 解析 f(x)==2 023+,
∴f(x)+f(-x)=4 047,
∴函数y=f(x)的图象关于点0,中心对称,
又M,N为函数f(x)=在[-a,a]上的最大值、最小值,故M+N=4 047.
22.-,+∞ 解析 (方法1)令F(x)=f(x)+fx-=当x>时,F(x)>+20=1+>1;当0F(0)=>1;当x≤0时,由F(x)=2x+>1,解得-1的x的取值范围是-,+∞.
(方法2)当x-≤0且x≤0时,由f(x)+fx->1得x+1+x-+1>1,得-1的x的取值范围是-,+∞.
23.解 (1)因为f(x)=,
所以f(-x)=.
由偶函数知f(-x)=f(x),解得a=1,
即f(x)==2x+,由对勾函数的性质知,当2x∈(0,1),即x∈(-∞,0)时函数单调递减,当2x∈(1,+∞),即x∈(0,+∞)时函数单调递增,所以函数f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
(2)由题意可得b22x++1≥2x+,
即b2x+2-2+1≥2x+,
令t=2x+∈2,,b(t2-2)+1≥t,
(方法1)g(t)=bt2-t+1-2b,若g(t)≥0在2,上有解,即g(t)max≥0.
若b<0,则g(t)max=g(2)=2b-1≥0,解得b≥,此时无解.
若b=0,则g(t)max=g(2)=-1,不符合题意.
若,即b≥,此时g(t)max=g=b-≥0,解得b≥,
若,即0综上,b的取值范围是,+∞.
(方法2)由b(t2-2)+1≥t得b≥,
令g(t)=,则b≥g(t)min.
g(t)=,所以b的取值范围是,+∞.
(方法3)由b(t2-2)+1≥t得,
令g(t)=,则≤g(t)max,g(t)==(t-1)-+2≤,所以b≥.
故b的取值范围是,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024数学学业水平考试专题练
优化集训6 指数与指数函数
基础巩固
1.函数f(x)=ab-x的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0
C.0
2.已知=5,那么等于( )
A. B.- C.± D.7
3.化简(a>0,b>0)的结果为( )
A. B.ab C. D.
4.若函数f(x)=有最大值3,则实数a的值为( )
A.-2 B.-1
C.1 D.2
5.已知a=0.20.3,b=0.20.5,c=0.30.3,则以下关系不正确的是( )
A.b
6.函数f(x)=的图象大致为( )
7.(多选)函数f(x)=2x,对任意的x1,x2,其中x1≠x2,则下列结论中正确的是( )
A.f(x1·x2)=f(x1)+f(x2)
B.f(x1+x2)=f(x1)·f(x2)
C.f(-x1)=
D.<0(x1≠0)
8.(多选)已知函数f(x)=,下列说法正确的有 ( )
A.f(x)的图象关于原点对称
B.f(x)的图象关于y轴对称
C.f(x)的值域为(-1,1)
D. x1,x2∈R,且x1≠x2,>0
9.2= .
10.0.02-(-1)0= .
11.若定义在R上的函数f(x)满足f(-x)=f(x)且在区间[0,+∞)上单调递减,f(x)的部分图象如图所示,则不等式f(x)≥|2x-1|的解集为 .
12.若a=2.50.4,b=2.50.3,c5=5,则a,b,c的大小关系为 .
13.若函数y=的值域为[0,+∞),则实数a的取值范围是 .
14.若f(x)=是R上的增函数,则实数a的取值范围为 .
15.若直线y=2a与函数y=|ax-1|(a>0,a≠1)的图象有两个公共点,则a的取值范围是 .
16.已知函数f(x)=4x+a·2x+3,a∈R.
(1)当a=-4时,x∈[0,2],求函数f(x)的值域;
(2)若对任意的x∈(0,+∞),f(x)>0恒成立,求实数a的取值范围.
17.已知函数f(x)=2x+k·2-x,k∈R.
(1)若函数f(x)为奇函数,求实数k的值;
(2)若对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.
能力提升
18.(多选)关于函数f(x)=,下列结论中正确的是( )
A.当a=0时,f(x)是增函数
B.当a=0时,f(x)的值域为(-1,+∞)
C.当a=1时,f(x)是奇函数
D.若f(x)的定义域为R,则a<2
19.(多选)已知a,b分别是方程2x+x=0,3x+x=0的两个实数根,则下列选项中正确的是( )
A.-1
21.已知a>0,函数f(x)=,x∈[-a,a]的最大值、最小值分别为M,N,则M+N= .
22.设函数f(x)=则满足f(x)+f(x-)>1的x的取值范围是 .
23.(2023浙江温州)已知函数f(x)=为偶函数.
(1)求出a的值,并写出单调区间;
(2)若存在x∈[0,1]使得不等式bf(2x)+1≥f(x)成立,求实数b的取值范围.
优化集训6 指数与指数函数
基础巩固
1.A
2.C 解析 当x>0时,>0,>0,此时>0;当x<0时,<0,<0,此时<0.
∵+2=5+2=7,
∴=±.故选C.
3.A 解析 原式==ab-1.故选A.
4.D 解析 由于函数f(x)=有最大值3,所以a>0,且当x=-时,f(x)取得最大值为f==3,故-1=1,=2,a=2.故选D.
5.D 解析 ∵指数函数y=0.2x为减函数,∴0.20.3>0.20.5,即a>b,∵幂函数y=x0.3是增函数,∴0.30.3>0.20.3,即c>a,a,b,c的大小关系为0
7.BC
8.ACD 解析 f(x)=的定义域为R,关于原点对称,f(-x)==-f(x),所以f(x)是奇函数,图象关于原点对称,故选项A正确,选项B不正确;f(x)==1-,因为2x>0,所以2x+1>1,所以0<<1,-2<<0,所以-1<1-<1,可得f(x)的值域为(-1,1),故选项C正确;设任意的x1
9. 解析 2=2×-(-2)++2+-2=.
10.-45 解析 0.02-(-1)0=-49+-1=-49+-1=-45.
11.[-2,1] 解析 由图可知f(-2)=f(2)=0.75,f(1)=1,
所以f(x)≥|2x-1|的解集为[-2,1].
12.b
13.(-∞,-2] 解析 设g(x)=4x+a·2x+1,若函数y=的值域为[0,+∞),则等价于[0,+∞)是g(x)值域的子集,y=g(x)=4x+a·2x+1=(2x)2+a·2x+1,设t=2x,则t>0,则y=h(t)=t2+at+1.∵h(0)=1>0,∴当图象的对称轴t=-≤0,即a≥0时,不满足条件.当t=->0,即a<0时,判别式Δ=a2-4≥0,即则a≤-2,即实数a的取值范围是(-∞,-2].
14.[4,8) 解析 ∵当x>1时,f(x)=ax单调递增,∴a>1,
∵一次函数在(-∞,1]上单调递增,∴4->0,a<8,
且当x=1时应有(4-)×1+2≤a1,解得a≥4.
综上可得,实数a的取值范围是[4,8).
15.(0,) 解析 当0
16.解 (1)当a=-4时,令t=2x,由x∈[0,2],得t∈[1,4],
y=t2-4t+3=(t-2)2-1,
当t=2时,ymin=-1;
当t=4时,ymax=3.
∴函数f(x)的值域为[-1,3].
(2)设t=2x,则t>1,f(x)>0对任意的x∈(0,+∞)恒成立,等价于t2+at+3>0对任意的t∈(1,+∞)恒成立,
∴a>-(t+)在(1,+∞)内恒成立,
∴a>.
设g(t)=-( t+),t>1,函数g(t)在(1,)内单调递增,在(,+∞)上单调递减,
∴g(t)max=g()=-2,
∴a>-2,即a的取值范围为(-2,+∞).
17.解 (1)因为f(x)=2x+k·2-x,k∈R是奇函数,
所以f(-x)=-f(x),x∈R,
即2-x+k·2x=-(2x+k·2-x),
所以k=-1.
(2)因为对任意的x∈[0,+∞),均有f(x)>2-x,
即2x+k·2-x>2-x成立,
所以1-k<22x对x≥0恒成立,所以1-k<.
因为y=22x在[0,+∞)上单调递增,所以(22x)min=1,
所以k>0,即k的取值范围为(0,+∞).
能力提升
18.ACD 解析 当a=0时,f(x)==1-,u=4x+1,由函数u=4x+1单调递增,知函数y=1-在(0,+∞)上单调递增,所以f(x)=1-在R上单调递增,A符合题意;因为4x+1>1,0<<1,-2<-<0,所以f(x)==1-∈(-1,1),B不符合题意;当a=1时,f(x)=定义域为R,而f(-x)==-f(x),所以f(x)是奇函数,C符合题意;若f(x)的定义域为R,则4x+1-a·2x≠0恒成立,即a≠,因为=2x+≥2,当且仅当2x=,即x=0时,等号成立,所以a<2,D符合题意.故选ACD.
19.BD 解析 函数y=2x,y=3x,y=-x在同一坐标系中的图象如下,
所以-1
20.(-∞,1]∪[3,+∞) 解析 当x≥0时,函数f(x)=-x-是减函数,且f(1)=-1,∴不等式f(x-2)≤-1 f(x-2)≤f(1),又函数是偶函数,∴|x-2|≥1,故x的取值范围是(-∞,1]∪[3,+∞).
21.4 047 解析 f(x)==2 023+,
∴f(x)+f(-x)=4 047,
∴函数y=f(x)的图象关于点0,中心对称,
又M,N为函数f(x)=在[-a,a]上的最大值、最小值,故M+N=4 047.
22.-,+∞ 解析 (方法1)令F(x)=f(x)+fx-=当x>时,F(x)>+20=1+>1;当0
(方法2)当x-≤0且x≤0时,由f(x)+fx->1得x+1+x-+1>1,得-
23.解 (1)因为f(x)=,
所以f(-x)=.
由偶函数知f(-x)=f(x),解得a=1,
即f(x)==2x+,由对勾函数的性质知,当2x∈(0,1),即x∈(-∞,0)时函数单调递减,当2x∈(1,+∞),即x∈(0,+∞)时函数单调递增,所以函数f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
(2)由题意可得b22x++1≥2x+,
即b2x+2-2+1≥2x+,
令t=2x+∈2,,b(t2-2)+1≥t,
(方法1)g(t)=bt2-t+1-2b,若g(t)≥0在2,上有解,即g(t)max≥0.
若b<0,则g(t)max=g(2)=2b-1≥0,解得b≥,此时无解.
若b=0,则g(t)max=g(2)=-1,不符合题意.
若,即b≥,此时g(t)max=g=b-≥0,解得b≥,
若,即0
(方法2)由b(t2-2)+1≥t得b≥,
令g(t)=,则b≥g(t)min.
g(t)=,所以b的取值范围是,+∞.
(方法3)由b(t2-2)+1≥t得,
令g(t)=,则≤g(t)max,g(t)==(t-1)-+2≤,所以b≥.
故b的取值范围是,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
