2024数学学业水平考试专题练--优化集训8 含绝对值的函数与不等式(含解析)
文档属性
| 名称 | 2024数学学业水平考试专题练--优化集训8 含绝对值的函数与不等式(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 444.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:41:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024数学学业水平考试专题练
优化集训8 含绝对值的函数与不等式
基础巩固
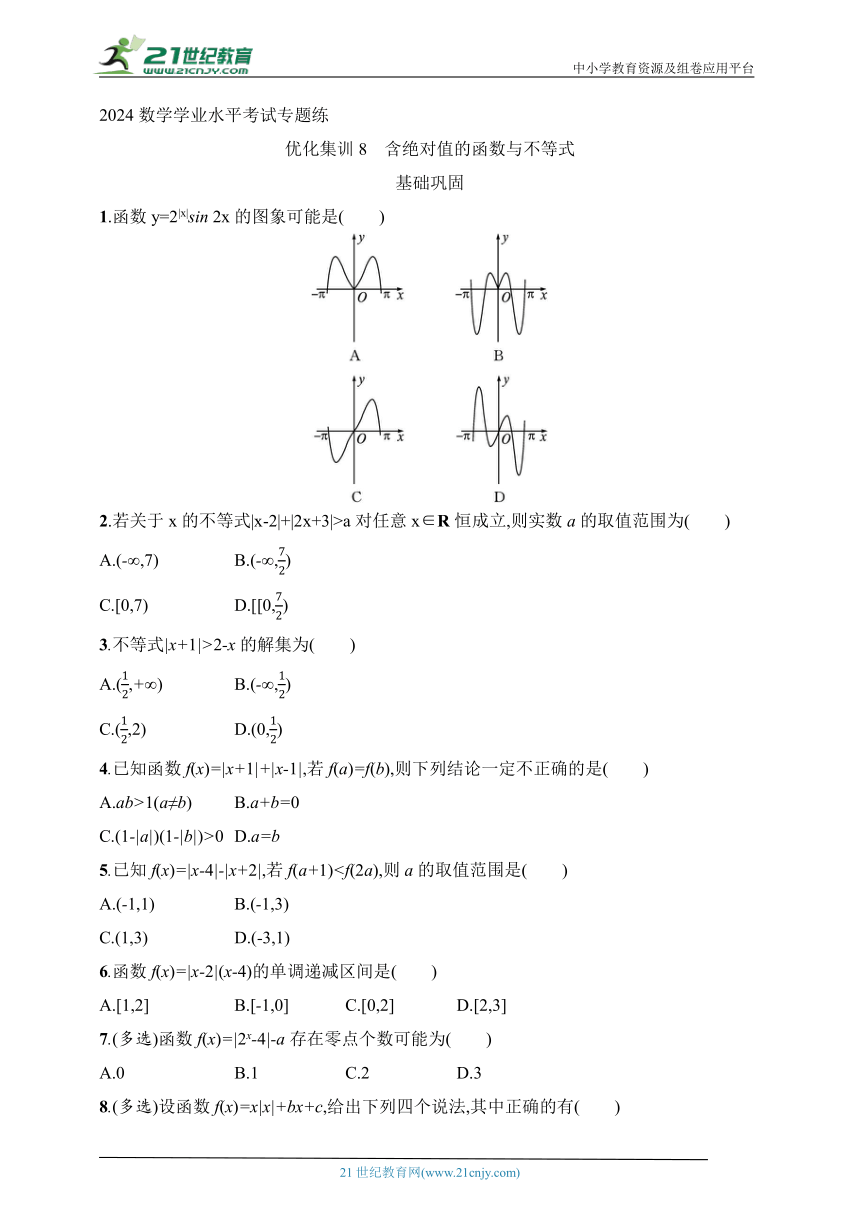
1.函数y=2|x|sin 2x的图象可能是( )
2.若关于x的不等式|x-2|+|2x+3|>a对任意x∈R恒成立,则实数a的取值范围为( )
A.(-∞,7) B.(-∞,)
C.[0,7) D.[[0,)
3.不等式|x+1|>2-x的解集为( )
A.(,+∞) B.(-∞,)
C.(,2) D.(0,)
4.已知函数f(x)=|x+1|+|x-1|,若f(a)=f(b),则下列结论一定不正确的是( )
A.ab>1(a≠b) B.a+b=0
C.(1-|a|)(1-|b|)>0 D.a=b
5.已知f(x)=|x-4|-|x+2|,若f(a+1)A.(-1,1) B.(-1,3)
C.(1,3) D.(-3,1)
6.函数f(x)=|x-2|(x-4)的单调递减区间是( )
A.[1,2] B.[-1,0] C.[0,2] D.[2,3]
7.(多选)函数f(x)=|2x-4|-a存在零点个数可能为( )
A.0 B.1 C.2 D.3
8.(多选)设函数f(x)=x|x|+bx+c,给出下列四个说法,其中正确的有( )
A.当c=0时,f(x)是奇函数
B.当b=0,c>0时,方程f(x)=0只有一个实数根
C.方程f(x)=0至多有两个实数根
D.f(x)的图象关于(0,c)对称
9.(2017浙江学考)若不等式|2x-a|+|x+1|≥1的解集为R,则实数a的取值范围为 .
10.若关于x的方程|x2-1|-x=m有4个不相等的实数根,则实数m的取值范围是 .
11.函数f(x)=x2-3|x|+2的单调递减区间是 .
12.对a,b∈R,记min{a,b}=若函数f(x)=min{|x+1|,|x-3|},当方程f(x)=m有2个不同的实根时,m的取值范围是 ,f(2x-1)≥f(2x)的解集是 .
13.已知函数f(x)=|x-a|+|x+3|.
(1)当a=1时,求不等式f(x)≥6的解集;
(2)若f(x)>-a恒成立,求a的取值范围.
14.已知函数f(x)=|x+a|+|x-1|.
(1)当a=3时,求不等式f(x)≥x+3a的解集;
(2)若f(x)≤|x-4|的解集包含[0,1],求a的取值范围.
15.(2023宁波中学)已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=1,解不等式f(x)≤1;
(2)若函数f(x)在[-2,2]上单调递增,求实数a的取值范围;
(3)记函数f(x)在[-2,2]上的最大值为g(a),求g(a)的最小值.
能力提升
16.已知函数f(x)=|x-3|+|x-a|的图象关于直线x=1对称,则实数a的取值为( )
A.-1 B.1 C.-3 D.3
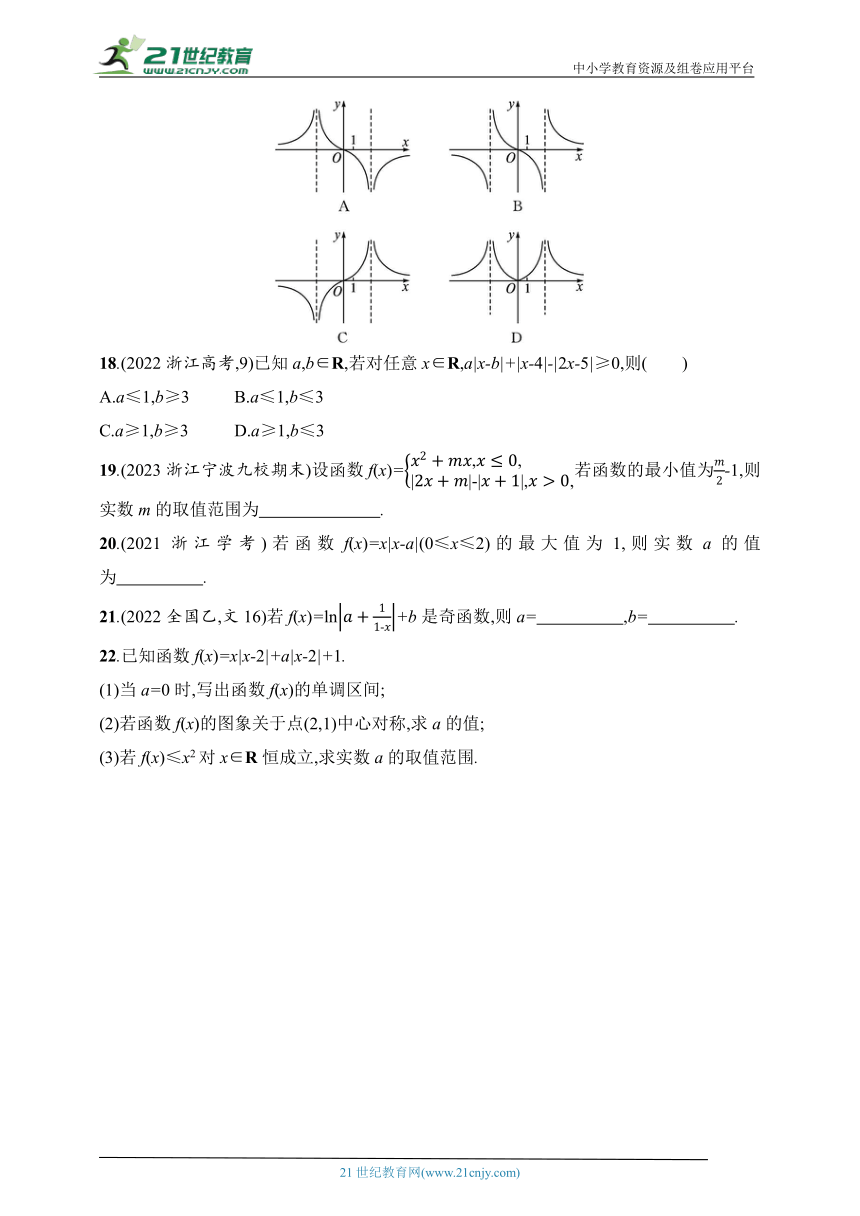
17.(2023浙江温州A卷)函数f(x)=ln||的图象大致为( )
18.(2022浙江高考,9)已知a,b∈R,若对任意x∈R,a|x-b|+|x-4|-|2x-5|≥0,则( )
A.a≤1,b≥3 B.a≤1,b≤3
C.a≥1,b≥3 D.a≥1,b≤3
19.(2023浙江宁波九校期末)设函数f(x)=若函数的最小值为-1,则实数m的取值范围为 .
20.(2021浙江学考)若函数f(x)=x|x-a|(0≤x≤2)的最大值为1,则实数a的值为 .
21.(2022全国乙,文16)若f(x)=ln+b是奇函数,则a= ,b= .
22.已知函数f(x)=x|x-2|+a|x-2|+1.
(1)当a=0时,写出函数f(x)的单调区间;
(2)若函数f(x)的图象关于点(2,1)中心对称,求a的值;
(3)若f(x)≤x2对x∈R恒成立,求实数a的取值范围.
优化集训8 含绝对值的函数与不等式
基础巩固
1.D 解析 因为在函数y=2|x|sin 2x中,y1=2|x|为偶函数,y2=sin 2x为奇函数,所以y=2|x|sin 2x为奇函数.所以排除选项A,B.当x=0,x=,x=π时,sin 2x=0,故函数y=2|x|sin 2x在[0,π]上有三个零点,排除选项C,故选D.
2.B 解析 由不等式恒成立转化为a<(|x-2|+|2x+3|)min,即转化为求|x-2|+|2x+3|的最小值.|x-2|+|2x+3|=|x-2|+|x+|+|x+|≥| (x-2)-(x+) |+|x+|=+|x+|≥,当x=-时,等号成立,即|x-2|+|2x+3|的最小值是,因为不等式|x-2|+|2x+3|>a对任意x∈R恒成立,所以a<(|x-2|+|2x+3|)min,即a<.故选B.
3.A 解析 由|x+1|>2-x可得解得x>.
4.A 解析 f(x)=|x+1|+|x-1|=又f(a)=f(b),①对于选项B,当a<-1,b>1,且a=-b时,满足题意,②对于选项C,当a≤-1,b≥1,且a=-b时,满足题意,③对于选项D,当-1≤a=b≤1时,满足题意,④结合①②③得,选项A一定不成立,故选A.
5.D 解析 f(x)=|x-4|-|x+2|=的图象,如图所示.
由图可知f(a+1)解得-3∴-3∴a的取值范围为(-3,1).
故选D.
6.D 解析 函数f(x)=的图象如图所示,所以f(x)的单调递减区间是[2,3].
故选D.
7.ABC 解析 函数f(x)=|2x-4|-a的零点个数可看作函数y=|2x-4|与y=a图象交点的个数,作出图象如下,
所以存在零点个数可能为0,1,2,故选ABC.
8.ABD 解析 对于A,当c=0时,函数f(x)=x|x|+bx,函数f(-x)=-x|-x|+b·(-x)=-(x|x|+bx)=-f(x),所以函数y=f(x)为奇函数,故A正确;对于B,当b=0,c>0时,f(x)=x|x|+c,因为函数f(x)在R上是增函数,且值域为(-∞,+∞),所以方程f(x)=0只有一个实数根,故B正确;对于C,当b=-1,c=0时,方程f(x)=0即x|x|-x=0有三个实根1,-1和0,故C错误;对于D,由函数y=x|x|+bx为奇函数,图象关于原点对称,所以y=f(x)的图象是由它的图象向上平移c个单位长度而得,所以函数y=f(x)的图象关于(0,c)对称,故D正确.故选ABD.
9.(-∞,-4]∪[0,+∞) 解析 设f(x)=|2x-a|+|x+1|,则题意等价于f(x)min=min{f(),f(-1)}≥1恒成立,min{f(),f(-1)}=min{|+1|,|a+2|}=|+1|,解|+1|≥1得a∈(-∞,-4]∪[0,+∞).
10.(1,) 解析 设f(x)=|x2-1|-x,则f(x)=故f(x)的图象如图所示,
由图象可得,若f(x)=m有4个不同的实数根,则111.(-∞,-],[0,] 解析 f(x)=当x≥0时,函数f(x)=x2-3x+2的单调递减区间为[0,],当x<0时,函数f(x)=x2+3x+2的单调递减区间为(-∞,-].
综上,函数f(x)的单调递减区间为[0,],(-∞,-].
12.{0}∪(2,+∞) (-∞,-]∪[] 解析 作出函数图象,由图可得f(x)=m有两个不相同的解,则m=0或m>2,不等式f(2x-1)≥f(2x)中,令2x=t,则f(t-1)≥f(t),由图象知,当t≤1时,|t-1+1|≥|t+1|,t2≥t2+2t+1,t≤-,即2x≤-,x≤-.当t-1≥1即t≥2时,|t-1-3|≥|t-3|,(t-4)2≥(t-3)2,t≤,2≤t≤,2≤2x≤,1≤x≤,当1综上,x≤-≤x≤.
13.解 (1)当a=1时,由f(x)≥6可得|x-1|+|x+3|≥6.
当x≤-3时,不等式可化为1-x-x-3≥6,
解得x≤-4;
当-3当x≥1时,不等式可化为x-1+x+3≥6,解得x≥2.
综上,原不等式的解集为(-∞,-4]∪[2,+∞).
(2)若f(x)>-a恒成立,则f(x)min>-a.
因为f(x)=|x-a|+|x+3|≥|(x-a)-(x+3)|=|a+3|(当且仅当(x-a)(x+3)≤0时,等号成立),
所以f(x)min=|a+3|,
所以|a+3|>-a,即a+3-a,
解得a∈(-,+∞).
故a的取值范围为(-,+∞).
14.解 (1)当a=3时,f(x)=
不等式f(x)≥x+3a,即f(x)≥x+9.
当x≤-3时,由-2x-2≥x+9,解得x≤-;
当-3当x≥1时,由2x+2≥x+9,解得x≥7.
综上,f(x)≥x+3a的解集为(-∞,-]∪[7,+∞).
(2)f(x)≤|x-4|等价于|x+a|≤|x-4|-|x-1|,
当x∈[0,1]时,|x+a|≤|x-4|-|x-1|等价于|x+a|≤3,即-3-a≤x≤3-a,
若f(x)≤|x-4|的解集包含[0,1],则
解得-3≤a≤2.
故a的取值范围为[-3,2].
15.解 (1)当a=1时,f(x)=
当x≥1时,f(x)≤1可化为2x2-2x+1≤1,解得x=1,
当x<1时,f(x)≤1可化为2x-1≤1,解得x<1.
综上,不等式的解集为{x|x≤1}.
(2)f(x)=
因为f(x)=2x2-(a+1)x+a的图象开口向上,对称轴为直线x=,
当=a,即a=时,f(x)在R上为增函数,满足题意;
当时,f(x)在R上为增函数,满足题意;
当>a,即a<时,为使函数f(x)在[-2,2]上单调递增,需满足≤-2,解得a≤-9.
综上,a的取值范围是(-∞,-9]∪[,+∞).
(3)由(2)知,当a≥或a≤-9时,f(x)在[-2,2]上单调递增,所以g(a)=f(2)=4+|2-a|;
当-9当-2当-1≤a<时,g(a)=max{f(a),f(2)}=max{a2,4+|2-a|},
因为a2-(4+|2-a|)=a2+a-6=(a+3)(a-2)<0,
所以g(a)=f(2)=4+|2-a|.
综上,g(a)=f(2)=4+|2-a|,当a=2时,g(a)min=4.
能力提升
16.A 解析 ∵函数y=|x-a|+|x-b|图象的对称轴为x=,
∴=1,解得a=-1.故选A.
17.A 解析 由题知,f(x)=ln||,所以||>0,解得定义域为{x|x≠±e},关于原点对称.
因为f(-x)=ln||=ln(||)-1=-ln||=-f(x),所以f(x)=ln||为奇函数,故D错误;
又因为f(1)=ln||f(2e)=ln||=ln<0,故B错误.故选A.
18.D 解析 可由特值法求得,D项满足题意,故选D.
19.{-1+}∪(-∞,0) 解析 ①当m=0时,f(x)= f(x)=
即f(x)=如图所示,由图知此时函数f(x)无最值,所以m≠0.
②当m>0时,f(x)=
f(x)=即f(x)=当x≤0时,f(x)=x2+mx的图象的对称轴为直线x=-<0,所以f(x)在(-∞,-)内单调递减,在(-,0)内单调递增,故f(x)min=f(-)=(-)2+m·(-)=-<0,当x>0时,f(x)=x+m-1单调递增,所以f(x)>f(0)=m-1,由函数f(x)的最小值为-1,此时(m-1)-(-1)=>0,所以函数最小值为-,
所以--1,即m2+2m-4=0,
解得m=-1+或m=-1-(舍去).
③当m<0时,由x≤0,f(x)=x2+mx,此时f(x)在(-∞,0]上单调递减,所以最小值为f(0)=0>-1,由x>0时,f(x)=|2x+m|-|x+1|=此时函数在(0,-)内单调递减,在(-,+∞)内单调递增,所以f(x)min=f(-)=-+m-1=-1,
所以当m<0时,函数最小值为-1满足题意.
综上所述,当函数f(x)最小值为-1时,实数m的取值范围为{-1+}∪(-∞,0).
20.2或 解析 若a≤0,则f(x)=x(x-a)≥x2,而y=x2在x∈[0,2]上最大值为4,故此时f(x)的最大值要大于等于4,不成立;若a>0,则必须有f(2)≤1,即|2-a|≤,得≤a≤,故此时∈[]在[0,2]这个区间,故必须也满足f()≤1即可,即≤1,即a≤2.综上,≤a≤2,而其最大值为1,则a=或2.
21.- ln 2 解析 由题设得函数f(x)的定义域关于原点对称,且定义域中x≠1,
∴将x=-1代入必有a+=0,即a=-.
∵x=0在定义域内,
∴f(0)=ln+b=0,
∴b=ln 2.
22.解 (1)当a=0时,∵f(x)=x|x-2|+1=
即f(x)=
∴f(x)在(-∞,1)内单调递增,在(1,2)内单调递减,在(2,+∞)内单调递增.
(2)若函数f(x)图象关于点(2,1)中心对称,则f(x+2)+f(2-x)=2.
令x=1,则f(1)+f(3)=2.
∴a+2+a+4=2,解得a=-2.
(3)①当x=2时,f(x)=1≤4恒成立,故a∈R.
②当x>2时,f(x)=x2+(a-2)x-2a+1,令x2+(a-2)x-2a+1≤x2,
则a≤=2+∈(2,+∞)恒成立,故a≤2.
当x<2时,f(x)=-x2+(2-a)x+2a+1,
令-x2+(2-a)x+2a+1≥x2,
a(2-x)-2x2+2x+1≤0,
∴a≤.
设h(x)=(x<2),
则h(x)==2(2-x)+-6≥2-6,
∴a≤2-6.
综上①②,a的取值范围是(-∞,2-6].
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024数学学业水平考试专题练
优化集训8 含绝对值的函数与不等式
基础巩固
1.函数y=2|x|sin 2x的图象可能是( )
2.若关于x的不等式|x-2|+|2x+3|>a对任意x∈R恒成立,则实数a的取值范围为( )
A.(-∞,7) B.(-∞,)
C.[0,7) D.[[0,)
3.不等式|x+1|>2-x的解集为( )
A.(,+∞) B.(-∞,)
C.(,2) D.(0,)
4.已知函数f(x)=|x+1|+|x-1|,若f(a)=f(b),则下列结论一定不正确的是( )
A.ab>1(a≠b) B.a+b=0
C.(1-|a|)(1-|b|)>0 D.a=b
5.已知f(x)=|x-4|-|x+2|,若f(a+1)
C.(1,3) D.(-3,1)
6.函数f(x)=|x-2|(x-4)的单调递减区间是( )
A.[1,2] B.[-1,0] C.[0,2] D.[2,3]
7.(多选)函数f(x)=|2x-4|-a存在零点个数可能为( )
A.0 B.1 C.2 D.3
8.(多选)设函数f(x)=x|x|+bx+c,给出下列四个说法,其中正确的有( )
A.当c=0时,f(x)是奇函数
B.当b=0,c>0时,方程f(x)=0只有一个实数根
C.方程f(x)=0至多有两个实数根
D.f(x)的图象关于(0,c)对称
9.(2017浙江学考)若不等式|2x-a|+|x+1|≥1的解集为R,则实数a的取值范围为 .
10.若关于x的方程|x2-1|-x=m有4个不相等的实数根,则实数m的取值范围是 .
11.函数f(x)=x2-3|x|+2的单调递减区间是 .
12.对a,b∈R,记min{a,b}=若函数f(x)=min{|x+1|,|x-3|},当方程f(x)=m有2个不同的实根时,m的取值范围是 ,f(2x-1)≥f(2x)的解集是 .
13.已知函数f(x)=|x-a|+|x+3|.
(1)当a=1时,求不等式f(x)≥6的解集;
(2)若f(x)>-a恒成立,求a的取值范围.
14.已知函数f(x)=|x+a|+|x-1|.
(1)当a=3时,求不等式f(x)≥x+3a的解集;
(2)若f(x)≤|x-4|的解集包含[0,1],求a的取值范围.
15.(2023宁波中学)已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=1,解不等式f(x)≤1;
(2)若函数f(x)在[-2,2]上单调递增,求实数a的取值范围;
(3)记函数f(x)在[-2,2]上的最大值为g(a),求g(a)的最小值.
能力提升
16.已知函数f(x)=|x-3|+|x-a|的图象关于直线x=1对称,则实数a的取值为( )
A.-1 B.1 C.-3 D.3
17.(2023浙江温州A卷)函数f(x)=ln||的图象大致为( )
18.(2022浙江高考,9)已知a,b∈R,若对任意x∈R,a|x-b|+|x-4|-|2x-5|≥0,则( )
A.a≤1,b≥3 B.a≤1,b≤3
C.a≥1,b≥3 D.a≥1,b≤3
19.(2023浙江宁波九校期末)设函数f(x)=若函数的最小值为-1,则实数m的取值范围为 .
20.(2021浙江学考)若函数f(x)=x|x-a|(0≤x≤2)的最大值为1,则实数a的值为 .
21.(2022全国乙,文16)若f(x)=ln+b是奇函数,则a= ,b= .
22.已知函数f(x)=x|x-2|+a|x-2|+1.
(1)当a=0时,写出函数f(x)的单调区间;
(2)若函数f(x)的图象关于点(2,1)中心对称,求a的值;
(3)若f(x)≤x2对x∈R恒成立,求实数a的取值范围.
优化集训8 含绝对值的函数与不等式
基础巩固
1.D 解析 因为在函数y=2|x|sin 2x中,y1=2|x|为偶函数,y2=sin 2x为奇函数,所以y=2|x|sin 2x为奇函数.所以排除选项A,B.当x=0,x=,x=π时,sin 2x=0,故函数y=2|x|sin 2x在[0,π]上有三个零点,排除选项C,故选D.
2.B 解析 由不等式恒成立转化为a<(|x-2|+|2x+3|)min,即转化为求|x-2|+|2x+3|的最小值.|x-2|+|2x+3|=|x-2|+|x+|+|x+|≥| (x-2)-(x+) |+|x+|=+|x+|≥,当x=-时,等号成立,即|x-2|+|2x+3|的最小值是,因为不等式|x-2|+|2x+3|>a对任意x∈R恒成立,所以a<(|x-2|+|2x+3|)min,即a<.故选B.
3.A 解析 由|x+1|>2-x可得解得x>.
4.A 解析 f(x)=|x+1|+|x-1|=又f(a)=f(b),①对于选项B,当a<-1,b>1,且a=-b时,满足题意,②对于选项C,当a≤-1,b≥1,且a=-b时,满足题意,③对于选项D,当-1≤a=b≤1时,满足题意,④结合①②③得,选项A一定不成立,故选A.
5.D 解析 f(x)=|x-4|-|x+2|=的图象,如图所示.
由图可知f(a+1)
故选D.
6.D 解析 函数f(x)=的图象如图所示,所以f(x)的单调递减区间是[2,3].
故选D.
7.ABC 解析 函数f(x)=|2x-4|-a的零点个数可看作函数y=|2x-4|与y=a图象交点的个数,作出图象如下,
所以存在零点个数可能为0,1,2,故选ABC.
8.ABD 解析 对于A,当c=0时,函数f(x)=x|x|+bx,函数f(-x)=-x|-x|+b·(-x)=-(x|x|+bx)=-f(x),所以函数y=f(x)为奇函数,故A正确;对于B,当b=0,c>0时,f(x)=x|x|+c,因为函数f(x)在R上是增函数,且值域为(-∞,+∞),所以方程f(x)=0只有一个实数根,故B正确;对于C,当b=-1,c=0时,方程f(x)=0即x|x|-x=0有三个实根1,-1和0,故C错误;对于D,由函数y=x|x|+bx为奇函数,图象关于原点对称,所以y=f(x)的图象是由它的图象向上平移c个单位长度而得,所以函数y=f(x)的图象关于(0,c)对称,故D正确.故选ABD.
9.(-∞,-4]∪[0,+∞) 解析 设f(x)=|2x-a|+|x+1|,则题意等价于f(x)min=min{f(),f(-1)}≥1恒成立,min{f(),f(-1)}=min{|+1|,|a+2|}=|+1|,解|+1|≥1得a∈(-∞,-4]∪[0,+∞).
10.(1,) 解析 设f(x)=|x2-1|-x,则f(x)=故f(x)的图象如图所示,
由图象可得,若f(x)=m有4个不同的实数根,则1
综上,函数f(x)的单调递减区间为[0,],(-∞,-].
12.{0}∪(2,+∞) (-∞,-]∪[] 解析 作出函数图象,由图可得f(x)=m有两个不相同的解,则m=0或m>2,不等式f(2x-1)≥f(2x)中,令2x=t,则f(t-1)≥f(t),由图象知,当t≤1时,|t-1+1|≥|t+1|,t2≥t2+2t+1,t≤-,即2x≤-,x≤-.当t-1≥1即t≥2时,|t-1-3|≥|t-3|,(t-4)2≥(t-3)2,t≤,2≤t≤,2≤2x≤,1≤x≤,当1
13.解 (1)当a=1时,由f(x)≥6可得|x-1|+|x+3|≥6.
当x≤-3时,不等式可化为1-x-x-3≥6,
解得x≤-4;
当-3
综上,原不等式的解集为(-∞,-4]∪[2,+∞).
(2)若f(x)>-a恒成立,则f(x)min>-a.
因为f(x)=|x-a|+|x+3|≥|(x-a)-(x+3)|=|a+3|(当且仅当(x-a)(x+3)≤0时,等号成立),
所以f(x)min=|a+3|,
所以|a+3|>-a,即a+3
解得a∈(-,+∞).
故a的取值范围为(-,+∞).
14.解 (1)当a=3时,f(x)=
不等式f(x)≥x+3a,即f(x)≥x+9.
当x≤-3时,由-2x-2≥x+9,解得x≤-;
当-3
综上,f(x)≥x+3a的解集为(-∞,-]∪[7,+∞).
(2)f(x)≤|x-4|等价于|x+a|≤|x-4|-|x-1|,
当x∈[0,1]时,|x+a|≤|x-4|-|x-1|等价于|x+a|≤3,即-3-a≤x≤3-a,
若f(x)≤|x-4|的解集包含[0,1],则
解得-3≤a≤2.
故a的取值范围为[-3,2].
15.解 (1)当a=1时,f(x)=
当x≥1时,f(x)≤1可化为2x2-2x+1≤1,解得x=1,
当x<1时,f(x)≤1可化为2x-1≤1,解得x<1.
综上,不等式的解集为{x|x≤1}.
(2)f(x)=
因为f(x)=2x2-(a+1)x+a的图象开口向上,对称轴为直线x=,
当=a,即a=时,f(x)在R上为增函数,满足题意;
当
当>a,即a<时,为使函数f(x)在[-2,2]上单调递增,需满足≤-2,解得a≤-9.
综上,a的取值范围是(-∞,-9]∪[,+∞).
(3)由(2)知,当a≥或a≤-9时,f(x)在[-2,2]上单调递增,所以g(a)=f(2)=4+|2-a|;
当-9
因为a2-(4+|2-a|)=a2+a-6=(a+3)(a-2)<0,
所以g(a)=f(2)=4+|2-a|.
综上,g(a)=f(2)=4+|2-a|,当a=2时,g(a)min=4.
能力提升
16.A 解析 ∵函数y=|x-a|+|x-b|图象的对称轴为x=,
∴=1,解得a=-1.故选A.
17.A 解析 由题知,f(x)=ln||,所以||>0,解得定义域为{x|x≠±e},关于原点对称.
因为f(-x)=ln||=ln(||)-1=-ln||=-f(x),所以f(x)=ln||为奇函数,故D错误;
又因为f(1)=ln||
18.D 解析 可由特值法求得,D项满足题意,故选D.
19.{-1+}∪(-∞,0) 解析 ①当m=0时,f(x)= f(x)=
即f(x)=如图所示,由图知此时函数f(x)无最值,所以m≠0.
②当m>0时,f(x)=
f(x)=即f(x)=当x≤0时,f(x)=x2+mx的图象的对称轴为直线x=-<0,所以f(x)在(-∞,-)内单调递减,在(-,0)内单调递增,故f(x)min=f(-)=(-)2+m·(-)=-<0,当x>0时,f(x)=x+m-1单调递增,所以f(x)>f(0)=m-1,由函数f(x)的最小值为-1,此时(m-1)-(-1)=>0,所以函数最小值为-,
所以--1,即m2+2m-4=0,
解得m=-1+或m=-1-(舍去).
③当m<0时,由x≤0,f(x)=x2+mx,此时f(x)在(-∞,0]上单调递减,所以最小值为f(0)=0>-1,由x>0时,f(x)=|2x+m|-|x+1|=此时函数在(0,-)内单调递减,在(-,+∞)内单调递增,所以f(x)min=f(-)=-+m-1=-1,
所以当m<0时,函数最小值为-1满足题意.
综上所述,当函数f(x)最小值为-1时,实数m的取值范围为{-1+}∪(-∞,0).
20.2或 解析 若a≤0,则f(x)=x(x-a)≥x2,而y=x2在x∈[0,2]上最大值为4,故此时f(x)的最大值要大于等于4,不成立;若a>0,则必须有f(2)≤1,即|2-a|≤,得≤a≤,故此时∈[]在[0,2]这个区间,故必须也满足f()≤1即可,即≤1,即a≤2.综上,≤a≤2,而其最大值为1,则a=或2.
21.- ln 2 解析 由题设得函数f(x)的定义域关于原点对称,且定义域中x≠1,
∴将x=-1代入必有a+=0,即a=-.
∵x=0在定义域内,
∴f(0)=ln+b=0,
∴b=ln 2.
22.解 (1)当a=0时,∵f(x)=x|x-2|+1=
即f(x)=
∴f(x)在(-∞,1)内单调递增,在(1,2)内单调递减,在(2,+∞)内单调递增.
(2)若函数f(x)图象关于点(2,1)中心对称,则f(x+2)+f(2-x)=2.
令x=1,则f(1)+f(3)=2.
∴a+2+a+4=2,解得a=-2.
(3)①当x=2时,f(x)=1≤4恒成立,故a∈R.
②当x>2时,f(x)=x2+(a-2)x-2a+1,令x2+(a-2)x-2a+1≤x2,
则a≤=2+∈(2,+∞)恒成立,故a≤2.
当x<2时,f(x)=-x2+(2-a)x+2a+1,
令-x2+(2-a)x+2a+1≥x2,
a(2-x)-2x2+2x+1≤0,
∴a≤.
设h(x)=(x<2),
则h(x)==2(2-x)+-6≥2-6,
∴a≤2-6.
综上①②,a的取值范围是(-∞,2-6].
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
