2024数学学业水平考试专题练--优化集训13 函数y=Asin(ωx+φ)(含解析)
文档属性
| 名称 | 2024数学学业水平考试专题练--优化集训13 函数y=Asin(ωx+φ)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 415.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:45:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024数学学业水平考试专题练
优化集训13 函数y=Asin(ωx+φ)
基础巩固
1.将函数y=sin(2x+φ)的图象沿x轴向左平移个单位长度后,得到一个偶函数的图象,则φ的一个可能取值为( )
A. B. C.0 D.
2.已知函数f(x)=2sin(2x+θ),θ∈R,若f=-2,则f(x)的一个单调递减区间是( )
A. B.-
C. D.-
3.设函数f(x)=cos在[-π,π]的图象大致如图所示,则f(x)的最小正周期为( )
A. B. C. D.
4.将函数f(x)=sin 2x的图象向右平移φ0<φ<个单位长度后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=,则φ=( )
A. B. C. D.
5.函数y=cos 2x的图象向右平移φ0<φ<个单位长度后,与函数y=sin2x-的图象重合,则φ=( )
A. B. C. D.
6.函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则( )
A.ω=,φ= B.ω=,φ=
C.ω=,φ= D.ω=,φ=
7.已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤f对于任意x∈R恒成立,且f>f(π),则f的值为( )
A.- B.0 C. D.
8.将函数y=cos x+sin x(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
A. B. C. D.
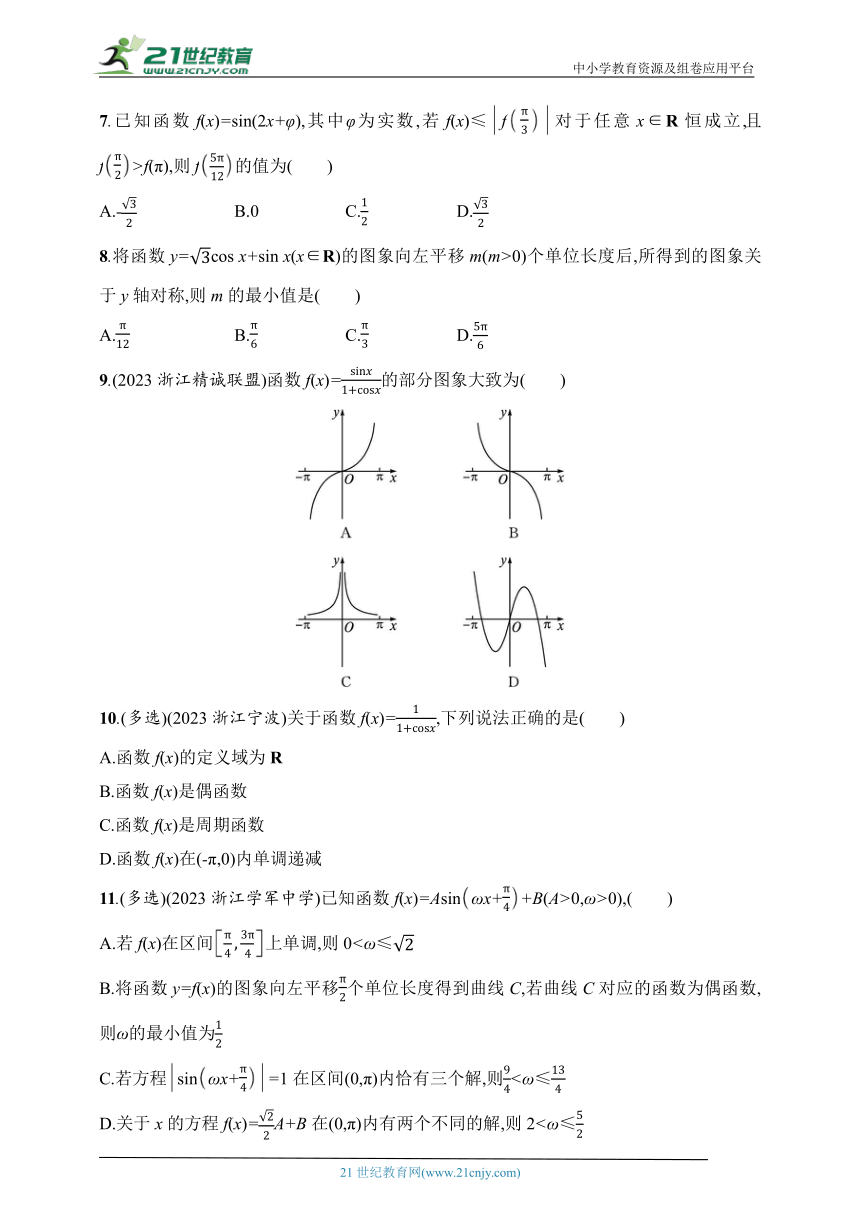
9.(2023浙江精诚联盟)函数f(x)=的部分图象大致为( )
10.(多选)(2023浙江宁波)关于函数f(x)=,下列说法正确的是( )
A.函数f(x)的定义域为R
B.函数f(x)是偶函数
C.函数f(x)是周期函数
D.函数f(x)在(-π,0)内单调递减
11.(多选)(2023浙江学军中学)已知函数f(x)=Asinωx++B(A>0,ω>0),( )
A.若f(x)在区间上单调,则0<ω≤
B.将函数y=f(x)的图象向左平移个单位长度得到曲线C,若曲线C对应的函数为偶函数,则ω的最小值为
C.若方程sinωx+=1在区间(0,π)内恰有三个解,则<ω≤
D.关于x的方程f(x)=A+B在(0,π)内有两个不同的解,则2<ω≤
12.若函数y=cos(2x+φ)|φ|<的图象关于点,0中心对称,则φ= .
13.函数y=2sin 2x+sin2x(x∈R)的最小正周期是 ,值域是 .
14.设函数f(x)=sin4x+,x∈0,.若关于x的方程f(x)=a有解,则实数a的取值范围是 .
15.(2023浙江大学附中)某游乐场的摩天轮示意图如图所示.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为24分钟.在圆周上均匀分布12个座舱,标号分别为1~12(可视为点),在旋转过程中,座舱与地面的距离h与时间t的函数关系基本符合正弦函数模型,现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为t分钟.
(1)求1号座舱与地面的距离h与时间t的函数关系h(t)的解析式;
(2)在前24分钟内,求1号座舱与地面的距离为17米时t的值;
(3)记1号座舱与5号座舱高度之差的绝对值为H米,求当H取得最大值时t的值.
16.已知函数f(x)=Acos(ωx+φ)+2(A>0,ω>0,0<φ<π)的最小值为1,最小正周期为π,且f(x)的图象关于直线x=对称.
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象向左平移个单位长度,得到函数y=g(x),求函数y=g(x)的单调递减区间.
能力提升
17.函数f(x)=sin x+acos x的图象关于直线x=对称,则实数a的值是( )
A. B.2
C. D.
18.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是奇函数,且f(x)的最小正周期为π,将y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g(x).若g=,则f=( )
A.-2 B.-
C. D.2
19.(多选)(2023浙江精诚联盟)已知函数f(x)=sin ωx-cos ωx,ω>0,则下列结论中正确的是 ( )
A.若ω=2,则将f(x)图象向左平移个单位长度后得到的图象关于原点对称
B.若|f(x1)-f(x2)|=4,且|x1-x2|的最小值为,则ω=2
C.若f(x)在0,上单调递增,则ω的取值范围为(0,3]
D.当ω=3时,f(x)在[0,π]上有且只有3个零点
20.(2023浙江嘉兴)已知函数f(x)=msinx--sin x+2在,2π上有两个不同的零点,则满足条件的所有m的值组成的集合是 .
21.(2023浙江丽水)已知函数f(x)=sin ωxcos ωx-sin2ωx+,其中ω>0,若实数x1,x2满足|f(x1)-f(x2)|=2,|x1-x2|的最小值为.
(1)求ω的值及f(x)的单调递减区间;
(2)若不等式f2(x)+2acos2x+-2a-2<0对任意x∈-恒成立,求实数a应满足的条件.
优化集训13 函数y=Asin(ωx+φ)
基础巩固
1.B 解析 将函数y=sin(2x+φ)的图象沿x轴向左平移个单位长度后,得到函数的图象对应的函数解析式为y=sin2x++φ=sin2x++φ,再根据所得函数为偶函数,可得+φ=kπ+,k∈Z,φ=kπ+,故φ的一个可能取值为,故选B.
2.D 解析 由f=2sin+θ=-2,则+θ=+2kπ(k∈Z),θ=+2kπ,则f(x)=2sin2x+,∴2kπ+≤2x+≤2kπ+,解得kπ-≤x≤+kπ,故选D.
3.C 解析 由题图知f=cos=0,所以-ω++kπ(k∈Z),化简得ω=-(k∈Z).因为T<2π<2T,即<2π<,所以1<|ω|<2,解得-4.D 解析 f(x)的图象向右平移φ个单位长度后,得到g(x)=sin(2x-2φ),又|f(x1)-g(x2)|=2,∴不妨令2x1=+2kπ,2x2-2φ=-+2mπ,∴x1-x2=-φ+(k-m)π,又|x1-x2|min=,∴-φ=,解得φ=,故选D.
5.C 解析 由y=cos 2(x-φ)=sin2x-2φ+=sin2x-,解得φ=.
6.C 解析 由图知=2,故T=8,由T=,得ω=.由图知,函数过(1,1),故+φ=2kπ+,k∈Z,从而φ=2kπ+,由题意取φ=.故选C.
7.D 解析 由条件,解得φ=-,∴f(x)=sin2x-,∴f=,故选D.
8.B 解析 由于y=cos x+sin x=2cosx-(x∈R),向左平移m(m>0)个单位长度后得函数y=2cosx+m-的图象,由于图象关于y轴对称,所以m-=kπ,于是m=+kπ,k∈Z,故当k=0时,m取最小值.故选B.
9.A 解析 因为f(-x)=-f(x),所以函数f(x)=是奇函数,当x∈(0,π)时,f(x)>0,故选A.
10.BCD 解析 由1+cos x≠0得cos x≠-1,所以x≠2kπ+π,k∈Z,所以f(x)的定义域是{x|x≠2kπ+π,k∈Z},故A选项错误.则f(x)的定义域关于原点对称,f(-x)==f(x),所以f(x)是偶函数,B选项正确.f(x+2π)==f(x),所以f(x)是周期函数,C选项正确.当x≠2kπ+π,k∈Z时,1+cos x>0恒成立,y=1+cos x在(-π,0)内单调递增,所以f(x)=在(-π,0)内单调递减,D选项正确.故选BCD.
11.BCD 解析 对于A,x∈,ωx+∈,若f(x)在区间上单调递增,则解得8k-3≤ω≤k+,又因为k∈Z,ω>0,所以0<ω≤,若f(x)在区间上单调递减,则解得8k+1≤ω≤,又因为k∈Z,ω>0,所以1≤ω≤.综上,0<ω≤或1≤ω≤,A错误;对于B,y=f(x)的图象向左平移个单位长度得到g(x)=Asinωx++B,若g(x)为偶函数,则有=kπ+,解得ω=2k+,k∈Z,而ω>0,所以ω最小值为,B正确;对于C,因为x∈(0,π),所以ωx+∈,ωπ+,函数y=sinωx+在(0,π)内恰有三个极值点,则有<ωπ+,解得<ω≤,C正确;对于D,f(x)=A+B,即sinωx+=,x∈(0,π),ωx+∈,ωπ+,则<ωπ+,解得2<ω≤,D正确.故选BCD.
12.- 解析 因为余弦函数y=cos x的图象的对称中心是+kπ,0(k∈Z),函数y=cos(2x+φ)|φ|<的图象关于点,0中心对称,所以2×+φ=+kπ,所以φ=-+kπ(k∈Z),因为|φ|<,所以φ=-.
13.π 解析 函数y=2sin 2x+sin2x=2sin 2x+sin(2x-φ)+,cos φ=,sin φ=(x∈R).∵-1≤sin(2x-φ)≤1,
∴sin(2x-φ)+,即函数的值域为,最小正周期T==π.
14.-,1 解析 令z=4x+,则当x∈0,时,z=4x+∈,作出函数y=sin z,z∈的图象(图略),直线y=a与之有公共点的条件是a∈-,1.
15.解 (1)设1号座舱与地面的距离h与时间t的函数关系的解析式为h(t)=Asin(ωt+φ)+b(A>0,ω>0,t≥0),则A=30,b=32,∴h(t)=30sin(ωt+φ)+32(ω>0).
依题意T=24 min,∴ω=(rad/min),
当t=0时,h(t)=32,∴φ=0,
∴h(t)=30sint+32(t≥0).
(2)令h(t)=17,即30sint+32=17,
∴sint=-.
∵0≤t≤24,∴0≤t≤2π,∴t=t=,
解得t=14或t=22,
∴t=14或t=22时,1号座舱与地面的距离为17米.
(3)设1号座舱与地面的距离为h1,5号座舱与地面的距离为h5,依题意,h1=30sint+32,h5=30sin(t+8)+32,
∴H=30sint+32-30sin(t+8)+32
=30sint-30sint+
=30sint-cost
=30sint-.
令t-+kπ,k∈N,解得t=8+12k(k∈N),
所以当t=8+12k(k∈N)时,H取得最大值.
16.解 (1)由题意可知-A+2=1,所以A=1,
又=π ω=2,此时f(x)=cos(2x+φ)+2,
由f(x)的图象关于直线x=对称可知2×+φ=kπ,k∈Z,所以φ=kπ-,k∈Z.
由于0<φ<π,故取k=1,则φ=,
故f(x)=cos2x++2.
(2)将函数y=f(x)的图象向左平移个单位长度,得到函数y=g(x)=fx+=cos2x++2=-sin 2x+2,
令-+2kπ≤2x≤+2kπ,k∈Z,解得-+kπ≤x≤+kπ,k∈Z,故y=g(x)的单调递减区间为-+kπ,+kπ,k∈Z.
能力提升
17.D 解析 由条件f(0)=f,解得a=,故选D.
18.C 解析 已知函数为奇函数,且|φ|<π,故φ=0.则f(x)=Asin ωx.∴g(x)=Asin.∵g(x)的最小正周期为2π,即=2π,∴ω=2.则g(x)=Asin x.由g=,得Asin ,解得A=2.则f(x)=2sin 2x.∴f=2sin .故选C.
19.ABD 解析 函数f(x)=sin ωx-cos ωx=2sinωx-,选项A,若ω=2,f(x)=2sin2x-,将f(x)图象向左平移个单位长度后得到y=2sin2x+-=2sin 2x,其图象关于原点对称,故正确;选项B,若|f(x1)-f(x2)|=4,且|x1-x2|的最小值为,则,解得ω=2,故正确;选项C,当x∈0,时,ωx-∈-,若f(x)在0,上单调递增,则,解得0<ω≤,故错误;选项D,当ω=3时,f(x)=2sin3x-,令3x-=kπ,k∈Z,解得x=,k∈Z,因为x∈[0,π],所以x=,x=,x=,所以f(x)在[0,π]有且只有3个零点,故正确.故选ABD.
20.{-3,-2} 解析 f(x)=msinx--cosx-+2=msinx-+2sin2x-+1,令t=sinx-∈[0,1],则f(t)=2t2+mt+1,t∈[0,1],当t∈0,∪{1}时,t=sinx-有1个根,当t∈,1时,t=sinx-有2个根,关于t的方程2t2+mt+1=0,显然t≠0,则m=-2t-∈(-∞,-2],当m∈(-∞,-3)时,m=-2t-有一个根t0∈0,,则t0=sinx-有1个根,故f(x)有1个零点;当m=-3时,m=-2t-有两个根t1,t2,其中t1∈0,,t2=1,t1=sinx-有1个根,t2=sinx-也有1个根,故f(x)有2个零点;当m∈(-3,-2)时,m=-2t-有两个根t1,t2,其中t1∈0,,t2∈,1,则t1=sinx-有1个根,t2=sinx-也有2个根,故f(x)有3个零点;当m=-2时,m=-2t-有一个根t0=,则t0=sinx-有2个根,故f(x)有2个零点.综上所述,当m=-3或m=-2时,f(x)有2个零点.
21.解 (1)由题意,函数f(x)=sin ωxcos ωx-sin2ωx+sin 2ωx-sin 2ωx+cos 2ωx=sin2ωx+,
因为|x1-x2|的最小值为,
所以f(x)的最小正周期T=π=,解得ω=1,
所以f(x)=sin2x+.
由2kπ+≤2x+≤2kπ+,k∈Z,
解得kπ+≤x≤kπ+,k∈Z,
所以f(x)的单调递减区间为kπ+,kπ+(k∈Z).
(2)由f2(x)+2acos2x+-2a-2=sin22x++2acos2x+-2a-2=-cos22x++2acos2x+-2a-1,
因为x∈-,可得2x+∈0,,
令t=cos2x+,则cos2x+∈(0,1),
所以-t2+2at-2a-1<0,t∈(0,1),即2a(t-1),
令m=t-1∈(-1,0),可得=m++2,
又因为函数y=m+在(-1,0)内单调递减,
所以m++2<-1,所以2a≥-1,解得a≥-,
即实数a的取值范围是-,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024数学学业水平考试专题练
优化集训13 函数y=Asin(ωx+φ)
基础巩固
1.将函数y=sin(2x+φ)的图象沿x轴向左平移个单位长度后,得到一个偶函数的图象,则φ的一个可能取值为( )
A. B. C.0 D.
2.已知函数f(x)=2sin(2x+θ),θ∈R,若f=-2,则f(x)的一个单调递减区间是( )
A. B.-
C. D.-
3.设函数f(x)=cos在[-π,π]的图象大致如图所示,则f(x)的最小正周期为( )
A. B. C. D.
4.将函数f(x)=sin 2x的图象向右平移φ0<φ<个单位长度后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=,则φ=( )
A. B. C. D.
5.函数y=cos 2x的图象向右平移φ0<φ<个单位长度后,与函数y=sin2x-的图象重合,则φ=( )
A. B. C. D.
6.函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则( )
A.ω=,φ= B.ω=,φ=
C.ω=,φ= D.ω=,φ=
7.已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤f对于任意x∈R恒成立,且f>f(π),则f的值为( )
A.- B.0 C. D.
8.将函数y=cos x+sin x(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
A. B. C. D.
9.(2023浙江精诚联盟)函数f(x)=的部分图象大致为( )
10.(多选)(2023浙江宁波)关于函数f(x)=,下列说法正确的是( )
A.函数f(x)的定义域为R
B.函数f(x)是偶函数
C.函数f(x)是周期函数
D.函数f(x)在(-π,0)内单调递减
11.(多选)(2023浙江学军中学)已知函数f(x)=Asinωx++B(A>0,ω>0),( )
A.若f(x)在区间上单调,则0<ω≤
B.将函数y=f(x)的图象向左平移个单位长度得到曲线C,若曲线C对应的函数为偶函数,则ω的最小值为
C.若方程sinωx+=1在区间(0,π)内恰有三个解,则<ω≤
D.关于x的方程f(x)=A+B在(0,π)内有两个不同的解,则2<ω≤
12.若函数y=cos(2x+φ)|φ|<的图象关于点,0中心对称,则φ= .
13.函数y=2sin 2x+sin2x(x∈R)的最小正周期是 ,值域是 .
14.设函数f(x)=sin4x+,x∈0,.若关于x的方程f(x)=a有解,则实数a的取值范围是 .
15.(2023浙江大学附中)某游乐场的摩天轮示意图如图所示.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为24分钟.在圆周上均匀分布12个座舱,标号分别为1~12(可视为点),在旋转过程中,座舱与地面的距离h与时间t的函数关系基本符合正弦函数模型,现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为t分钟.
(1)求1号座舱与地面的距离h与时间t的函数关系h(t)的解析式;
(2)在前24分钟内,求1号座舱与地面的距离为17米时t的值;
(3)记1号座舱与5号座舱高度之差的绝对值为H米,求当H取得最大值时t的值.
16.已知函数f(x)=Acos(ωx+φ)+2(A>0,ω>0,0<φ<π)的最小值为1,最小正周期为π,且f(x)的图象关于直线x=对称.
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象向左平移个单位长度,得到函数y=g(x),求函数y=g(x)的单调递减区间.
能力提升
17.函数f(x)=sin x+acos x的图象关于直线x=对称,则实数a的值是( )
A. B.2
C. D.
18.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是奇函数,且f(x)的最小正周期为π,将y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g(x).若g=,则f=( )
A.-2 B.-
C. D.2
19.(多选)(2023浙江精诚联盟)已知函数f(x)=sin ωx-cos ωx,ω>0,则下列结论中正确的是 ( )
A.若ω=2,则将f(x)图象向左平移个单位长度后得到的图象关于原点对称
B.若|f(x1)-f(x2)|=4,且|x1-x2|的最小值为,则ω=2
C.若f(x)在0,上单调递增,则ω的取值范围为(0,3]
D.当ω=3时,f(x)在[0,π]上有且只有3个零点
20.(2023浙江嘉兴)已知函数f(x)=msinx--sin x+2在,2π上有两个不同的零点,则满足条件的所有m的值组成的集合是 .
21.(2023浙江丽水)已知函数f(x)=sin ωxcos ωx-sin2ωx+,其中ω>0,若实数x1,x2满足|f(x1)-f(x2)|=2,|x1-x2|的最小值为.
(1)求ω的值及f(x)的单调递减区间;
(2)若不等式f2(x)+2acos2x+-2a-2<0对任意x∈-恒成立,求实数a应满足的条件.
优化集训13 函数y=Asin(ωx+φ)
基础巩固
1.B 解析 将函数y=sin(2x+φ)的图象沿x轴向左平移个单位长度后,得到函数的图象对应的函数解析式为y=sin2x++φ=sin2x++φ,再根据所得函数为偶函数,可得+φ=kπ+,k∈Z,φ=kπ+,故φ的一个可能取值为,故选B.
2.D 解析 由f=2sin+θ=-2,则+θ=+2kπ(k∈Z),θ=+2kπ,则f(x)=2sin2x+,∴2kπ+≤2x+≤2kπ+,解得kπ-≤x≤+kπ,故选D.
3.C 解析 由题图知f=cos=0,所以-ω++kπ(k∈Z),化简得ω=-(k∈Z).因为T<2π<2T,即<2π<,所以1<|ω|<2,解得-
5.C 解析 由y=cos 2(x-φ)=sin2x-2φ+=sin2x-,解得φ=.
6.C 解析 由图知=2,故T=8,由T=,得ω=.由图知,函数过(1,1),故+φ=2kπ+,k∈Z,从而φ=2kπ+,由题意取φ=.故选C.
7.D 解析 由条件,解得φ=-,∴f(x)=sin2x-,∴f=,故选D.
8.B 解析 由于y=cos x+sin x=2cosx-(x∈R),向左平移m(m>0)个单位长度后得函数y=2cosx+m-的图象,由于图象关于y轴对称,所以m-=kπ,于是m=+kπ,k∈Z,故当k=0时,m取最小值.故选B.
9.A 解析 因为f(-x)=-f(x),所以函数f(x)=是奇函数,当x∈(0,π)时,f(x)>0,故选A.
10.BCD 解析 由1+cos x≠0得cos x≠-1,所以x≠2kπ+π,k∈Z,所以f(x)的定义域是{x|x≠2kπ+π,k∈Z},故A选项错误.则f(x)的定义域关于原点对称,f(-x)==f(x),所以f(x)是偶函数,B选项正确.f(x+2π)==f(x),所以f(x)是周期函数,C选项正确.当x≠2kπ+π,k∈Z时,1+cos x>0恒成立,y=1+cos x在(-π,0)内单调递增,所以f(x)=在(-π,0)内单调递减,D选项正确.故选BCD.
11.BCD 解析 对于A,x∈,ωx+∈,若f(x)在区间上单调递增,则解得8k-3≤ω≤k+,又因为k∈Z,ω>0,所以0<ω≤,若f(x)在区间上单调递减,则解得8k+1≤ω≤,又因为k∈Z,ω>0,所以1≤ω≤.综上,0<ω≤或1≤ω≤,A错误;对于B,y=f(x)的图象向左平移个单位长度得到g(x)=Asinωx++B,若g(x)为偶函数,则有=kπ+,解得ω=2k+,k∈Z,而ω>0,所以ω最小值为,B正确;对于C,因为x∈(0,π),所以ωx+∈,ωπ+,函数y=sinωx+在(0,π)内恰有三个极值点,则有<ωπ+,解得<ω≤,C正确;对于D,f(x)=A+B,即sinωx+=,x∈(0,π),ωx+∈,ωπ+,则<ωπ+,解得2<ω≤,D正确.故选BCD.
12.- 解析 因为余弦函数y=cos x的图象的对称中心是+kπ,0(k∈Z),函数y=cos(2x+φ)|φ|<的图象关于点,0中心对称,所以2×+φ=+kπ,所以φ=-+kπ(k∈Z),因为|φ|<,所以φ=-.
13.π 解析 函数y=2sin 2x+sin2x=2sin 2x+sin(2x-φ)+,cos φ=,sin φ=(x∈R).∵-1≤sin(2x-φ)≤1,
∴sin(2x-φ)+,即函数的值域为,最小正周期T==π.
14.-,1 解析 令z=4x+,则当x∈0,时,z=4x+∈,作出函数y=sin z,z∈的图象(图略),直线y=a与之有公共点的条件是a∈-,1.
15.解 (1)设1号座舱与地面的距离h与时间t的函数关系的解析式为h(t)=Asin(ωt+φ)+b(A>0,ω>0,t≥0),则A=30,b=32,∴h(t)=30sin(ωt+φ)+32(ω>0).
依题意T=24 min,∴ω=(rad/min),
当t=0时,h(t)=32,∴φ=0,
∴h(t)=30sint+32(t≥0).
(2)令h(t)=17,即30sint+32=17,
∴sint=-.
∵0≤t≤24,∴0≤t≤2π,∴t=t=,
解得t=14或t=22,
∴t=14或t=22时,1号座舱与地面的距离为17米.
(3)设1号座舱与地面的距离为h1,5号座舱与地面的距离为h5,依题意,h1=30sint+32,h5=30sin(t+8)+32,
∴H=30sint+32-30sin(t+8)+32
=30sint-30sint+
=30sint-cost
=30sint-.
令t-+kπ,k∈N,解得t=8+12k(k∈N),
所以当t=8+12k(k∈N)时,H取得最大值.
16.解 (1)由题意可知-A+2=1,所以A=1,
又=π ω=2,此时f(x)=cos(2x+φ)+2,
由f(x)的图象关于直线x=对称可知2×+φ=kπ,k∈Z,所以φ=kπ-,k∈Z.
由于0<φ<π,故取k=1,则φ=,
故f(x)=cos2x++2.
(2)将函数y=f(x)的图象向左平移个单位长度,得到函数y=g(x)=fx+=cos2x++2=-sin 2x+2,
令-+2kπ≤2x≤+2kπ,k∈Z,解得-+kπ≤x≤+kπ,k∈Z,故y=g(x)的单调递减区间为-+kπ,+kπ,k∈Z.
能力提升
17.D 解析 由条件f(0)=f,解得a=,故选D.
18.C 解析 已知函数为奇函数,且|φ|<π,故φ=0.则f(x)=Asin ωx.∴g(x)=Asin.∵g(x)的最小正周期为2π,即=2π,∴ω=2.则g(x)=Asin x.由g=,得Asin ,解得A=2.则f(x)=2sin 2x.∴f=2sin .故选C.
19.ABD 解析 函数f(x)=sin ωx-cos ωx=2sinωx-,选项A,若ω=2,f(x)=2sin2x-,将f(x)图象向左平移个单位长度后得到y=2sin2x+-=2sin 2x,其图象关于原点对称,故正确;选项B,若|f(x1)-f(x2)|=4,且|x1-x2|的最小值为,则,解得ω=2,故正确;选项C,当x∈0,时,ωx-∈-,若f(x)在0,上单调递增,则,解得0<ω≤,故错误;选项D,当ω=3时,f(x)=2sin3x-,令3x-=kπ,k∈Z,解得x=,k∈Z,因为x∈[0,π],所以x=,x=,x=,所以f(x)在[0,π]有且只有3个零点,故正确.故选ABD.
20.{-3,-2} 解析 f(x)=msinx--cosx-+2=msinx-+2sin2x-+1,令t=sinx-∈[0,1],则f(t)=2t2+mt+1,t∈[0,1],当t∈0,∪{1}时,t=sinx-有1个根,当t∈,1时,t=sinx-有2个根,关于t的方程2t2+mt+1=0,显然t≠0,则m=-2t-∈(-∞,-2],当m∈(-∞,-3)时,m=-2t-有一个根t0∈0,,则t0=sinx-有1个根,故f(x)有1个零点;当m=-3时,m=-2t-有两个根t1,t2,其中t1∈0,,t2=1,t1=sinx-有1个根,t2=sinx-也有1个根,故f(x)有2个零点;当m∈(-3,-2)时,m=-2t-有两个根t1,t2,其中t1∈0,,t2∈,1,则t1=sinx-有1个根,t2=sinx-也有2个根,故f(x)有3个零点;当m=-2时,m=-2t-有一个根t0=,则t0=sinx-有2个根,故f(x)有2个零点.综上所述,当m=-3或m=-2时,f(x)有2个零点.
21.解 (1)由题意,函数f(x)=sin ωxcos ωx-sin2ωx+sin 2ωx-sin 2ωx+cos 2ωx=sin2ωx+,
因为|x1-x2|的最小值为,
所以f(x)的最小正周期T=π=,解得ω=1,
所以f(x)=sin2x+.
由2kπ+≤2x+≤2kπ+,k∈Z,
解得kπ+≤x≤kπ+,k∈Z,
所以f(x)的单调递减区间为kπ+,kπ+(k∈Z).
(2)由f2(x)+2acos2x+-2a-2=sin22x++2acos2x+-2a-2=-cos22x++2acos2x+-2a-1,
因为x∈-,可得2x+∈0,,
令t=cos2x+,则cos2x+∈(0,1),
所以-t2+2at-2a-1<0,t∈(0,1),即2a(t-1)
令m=t-1∈(-1,0),可得=m++2,
又因为函数y=m+在(-1,0)内单调递减,
所以m++2<-1,所以2a≥-1,解得a≥-,
即实数a的取值范围是-,+∞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
