2024数学学业水平考试专题练--优化集训22 统计(含解析)
文档属性
| 名称 | 2024数学学业水平考试专题练--优化集训22 统计(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:52:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024数学学业水平考试专题练
优化集训22 统计
基础巩固
1.用抽签法进行抽样有以下几个步骤:
①将总体中的个体编号;
②把号码写在形状、大小相同的号签上(号签可以用小球、卡片、纸条制作);
③将这些号签放在一个容器内并搅拌均匀;
④从这个容器中逐个不放回地抽取号签,将取出号签所对应的个体作为样本.
这些步骤的先后顺序应为( )
A.①②③④ B.②③④①
C.①③④② D.①④②③
2.下列问题中,最适合用简单随机抽样法抽样的是 ( )
A.某电影院有32排座位,每排有40个座位,座位号是1~40,有一次报告会坐满了听众,报告会结束以后为听取意见,需留下32名听众进行座谈
B.从10台冰箱中抽出3台进行质量检查
C.某学校有在编人员160人,其中行政人员16人,教师112人,后勤人员32人,教育部门为了了解学校机构改革意见,要从中抽取一个容量为20的样本
D.某乡有山地8 000 km2,丘陵12 000 km2,平地24 000 km2,洼地4 000 km2,现抽取480 km2估计全乡农田的平均产量
3.(2023浙江绍兴)某组数据33,36,38,39,42,46,49,49,51,56的第80百分位数为( )
A.46 B.49
C.50 D.51
4.(2023浙江丽水)某中学组织三个年级的学生进行党史知识竞赛.经统计,得到成绩前200名学生分布的扇形图(如图)和成绩前200名中高一学生排名分布的条形图(如图),则下列说法错误的是( )
成绩前200名学生分布的扇形图
成绩前200名中高一学生排名分布的条形图
A.成绩前200名的学生中,高一人数比高二人数多30
B.成绩前100名的学生中,高一人数不超过50
C.成绩前50名的学生中,高三人数不超过32
D.成绩第51名到第100名的学生中,高二人数比高一人数多
5.(2023浙江丽水)某演讲比赛共有9位评委,分别给出某选手的原始评分9.2,9.5,9.6,9.1,9.3,9.0,8.8,9.3,9.7,评定该选手的成绩时,从9个原始评分中去掉1个最高分和1个最低分,得到7个有效评分.这7个有效评分与9个原始评分相比,不变的数字特征是( )
A.极差 B.中位数 C.平均数 D.方差
6.某城市某年1月到10月中每月空气质量为中度污染的天数分别为1,4,7,9,a,b,13,14,15,17,且9≤a≤b≤13.已知样本的中位数为10,则该样本的方差的最小值为( )
A.21.4 B.22.6 C.22.9 D.23.5
7.四名同学各掷骰子5次,记录每次骰子出现的点数并分别对每位同学掷得的点数进行统计处理,在四名同学以下的统计结果中,可以判断出该同学所掷骰子一定没有出现点数1的是( )
A.平均数为4,中位数为5
B.平均数为5,方差为2.4
C.中位数为4,众数为5
D.中位数为4,方差为2.8
8.某学校有男生400人,女生600人.为调查该校全体学生每天睡眠时间,采用分层随机抽样的方法抽取样本,计算得男生每天睡眠时间均值为7.5小时,方差为1,女生每天睡眠时间均值为7小时,方差为0.5.若男、女样本量按比例分配,则可估计总体方差为( )
A.0.45 B.0.62 C.0.7 D.0.76
9.数据30,29,28,27,26,24,23,22的中位数为( )
A.26 B.27 C.26和27 D.26.5
10.(多选)某公司为检测某型号汽车的质量问题,需对三个批次生产的该型号汽车进行检测,三个批次产量分别为100 000辆、150 000辆和250 000辆,公司质监部门计划从中抽取500辆进行检测,则下列说法正确的有( )
A.样本容量为500
B.采用简单随机抽样比分层随机抽样合适
C.应采用分层随机抽样,三个批次的汽车被抽到的概率不相等
D.应采用分层随机抽样,三个批次分别抽取100辆、150辆、250辆
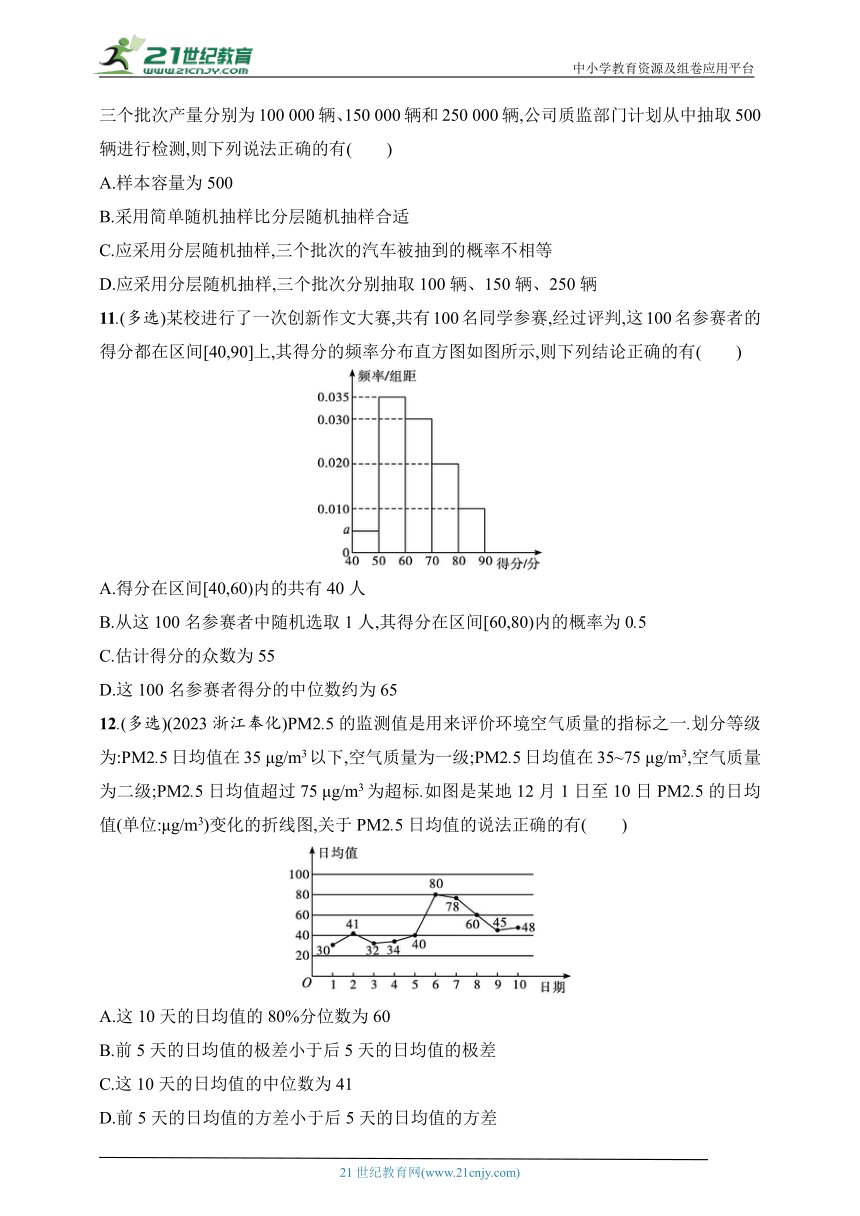
11.(多选)某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在区间[40,90]上,其得分的频率分布直方图如图所示,则下列结论正确的有( )
A.得分在区间[40,60)内的共有40人
B.从这100名参赛者中随机选取1人,其得分在区间[60,80)内的概率为0.5
C.估计得分的众数为55
D.这100名参赛者得分的中位数约为65
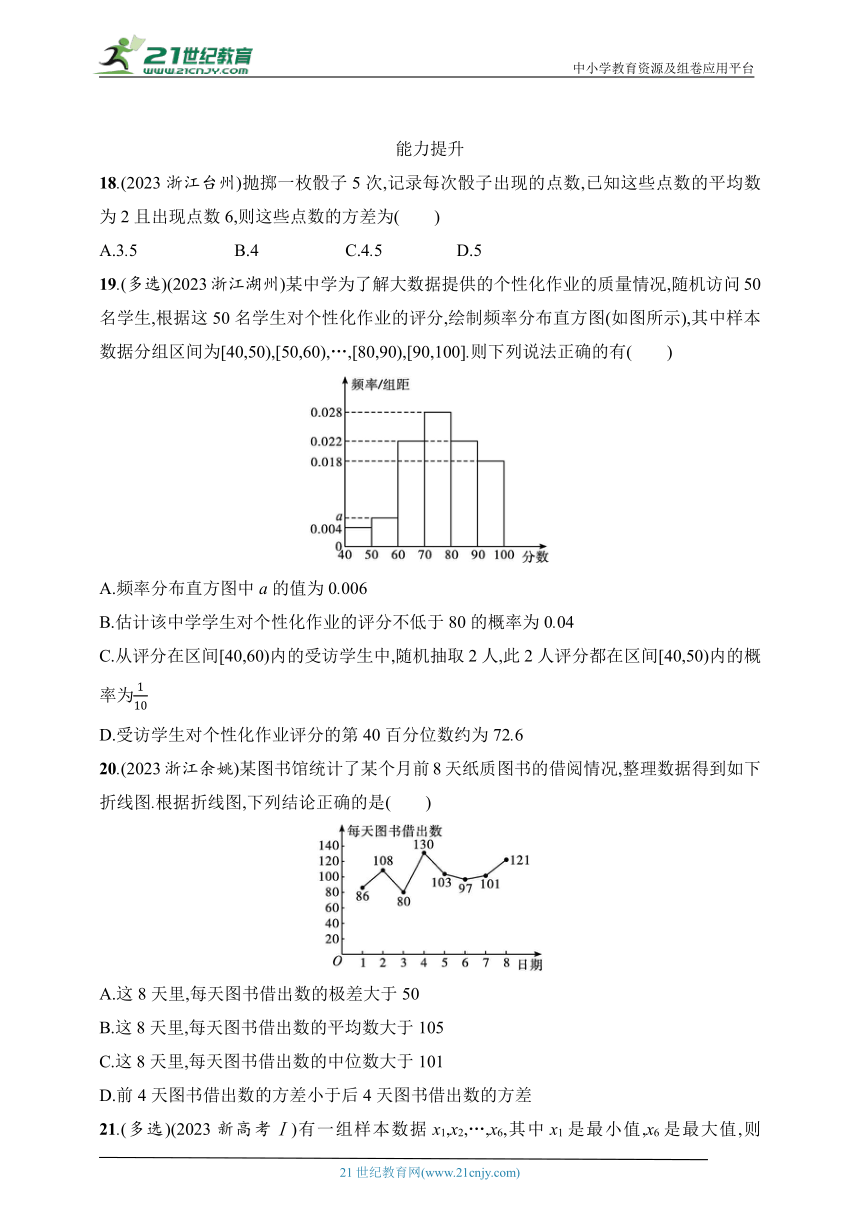
12.(多选)(2023浙江奉化)PM2.5的监测值是用来评价环境空气质量的指标之一.划分等级为:PM2.5日均值在35 μg/m3以下,空气质量为一级;PM2.5日均值在35~75 μg/m3,空气质量为二级;PM2.5日均值超过75 μg/m3为超标.如图是某地12月1日至10日PM2.5的日均值(单位:μg/m3)变化的折线图,关于PM2.5日均值的说法正确的有( )
A.这10天的日均值的80%分位数为60
B.前5天的日均值的极差小于后5天的日均值的极差
C.这10天的日均值的中位数为41
D.前5天的日均值的方差小于后5天的日均值的方差
13.某小区2018年至2023年家庭年平均收入X(单位:万元)与年平均支出Y(单位:万元)的统计资料如下表所示:
年份 2018 2019 2020 2021 2022 2023
收入X 11.5 12.1 13 13.4 14.2 15
支出Y 7.8 8.6 9.2 9.8 10.4 10.6
根据统计资料,该小区家庭年平均收入的中位数是a,家庭年平均支出的平均数为b,则a+b= .
14.若样本a1,a2,a3的方差是2,则样本2a1+3,2a2+3,2a3+3的标准差是 .
15.已知一组数据15,17,14,10,15,17,17,16,14,12,则该组数据的众数是 .
16.(2023浙江湖州)已知采用分层随机抽样的方法得到的高三男生、女生各100名学生的身高情况为:男生平均身高为172 cm,方差为120,女生平均身高为165 cm,方差为120,则总的样本方差是 .
17.某校对100名高一学生的某次数学测试成绩进行统计,分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示频率分布直方图.
(1)求图中a的值;
(2)估计该校学生数学成绩的平均数;
(3)估计该校学生数学成绩的第75百分位数.
能力提升
18.(2023浙江台州)抛掷一枚骰子5次,记录每次骰子出现的点数,已知这些点数的平均数为2且出现点数6,则这些点数的方差为( )
A.3.5 B.4 C.4.5 D.5
19.(多选)(2023浙江湖州)某中学为了解大数据提供的个性化作业的质量情况,随机访问50名学生,根据这50名学生对个性化作业的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].则下列说法正确的有( )
A.频率分布直方图中a的值为0.006
B.估计该中学学生对个性化作业的评分不低于80的概率为0.04
C.从评分在区间[40,60)内的受访学生中,随机抽取2人,此2人评分都在区间[40,50)内的概率为
D.受访学生对个性化作业评分的第40百分位数约为72.6
20.(2023浙江余姚)某图书馆统计了某个月前8天纸质图书的借阅情况,整理数据得到如下折线图.根据折线图,下列结论正确的是( )
A.这8天里,每天图书借出数的极差大于50
B.这8天里,每天图书借出数的平均数大于105
C.这8天里,每天图书借出数的中位数大于101
D.前4天图书借出数的方差小于后4天图书借出数的方差
21.(多选)(2023新高考Ⅰ)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则 ( )
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
22.(2023浙江衢州)某学校对该校学生每周零花钱的数额进行了随机调查,现将统计数据按区间[0,20),[20,40),…,[120,140]分组后绘成如图所示的频率分布直方图,已知a=3b.
(1)求频率分布直方图中a,b的值;
(2)估计该校学生每周零花钱的第55百分位数;
(3)若按照各组频率的比例采用分层随机抽样的方法从每周零花钱在区间[60,120)内的学生中抽取11人,求在区间[100,120)内抽取的人数.
优化集训22 统计
基础巩固
1.A 解析 利用抽签法第一步要进行编号,然后做号签,放入容器,最后按照逐个不放回地抽取号签.故这些步骤的先后顺序应为①②③④.故选A.
2.B 解析 根据总体数据特点分别适用哪种抽样特点,选取适当的抽样方法即可.对于A,数量大,不适合;
对于B,从10台冰箱中抽出3台进行质量检查,适合简单随机抽样;
对于C,D,适合分层随机抽样.故选B.
3.C 解析 ∵10×80%=8,∴第80百分位数为×(49+51)=50.故选C.
4.D 解析 由扇形图,成绩前200名的200人中,高一人数比高二人数多200×(45%-30%)=30,故A正确;
由条形图知,成绩前200名中高一学生排名分布在前100和后100的人数相等,因此成绩前100名的学生中,高一人数为200×45%×=45<50,故B正确;
成绩前50名的学生中,高一人数为200×45%×0.2=18,因此高三最多有32人,故C正确;
成绩在第51到100名的学生中,高一人数为200×45%×0.3=27,故高二最多有23人,因此高二人数比高一少,故D错误.
故选D.
5.B
6.B 解析 由题可知,a+b=20,则该组数据的平均数为=10,
方差s2=,
当且仅当a=b=10时,方差最小,且最小值为s2==22.6.
故选B.
7.B 解析 对于A,1,2,5,6,6符合条件,故A错误;
对于B,若平均数为5且出现点数1,则只能为1,6,6,6,6,此时方差为=4,故B正确;
对于C,1,2,4,5,5符合条件,故C错误;
对于D,1,4,4,5,6平均数为×(1+4+4+5+6)=4,方差为×[(1-4)2+(5-4)2+(6-4)2]=2.8,符合条件,故D错误.
故选B.
8.D 解析 由题意计算总体样本平均数为x=0.4×7.5+0.6×7=7.2,故所求总体方差s2=0.4×[1+(7.5-7.2)2]+0.6×[0.5+(7-7.2)2]=0.76.
故选D.
9.D 解析 因为数据为30,29,28,27,26,24,23,22,所以中位数为=26.5.故选D.
10.AD
11.ABC 解析 根据频率和为1,由(a+0.035+0.030+0.020+0.010)×10=1,解得a=0.005,
得分在区间[40,60)内的频率是0.40,得分在区间[40,60)内的有100×0.40=40(人),故A正确;
得分在区间[60,80)内的频率为0.5,可得从这100名参赛者中随机选取一人,得分在区间[60,80)内的概率为0.5,故B正确;
根据频率分布直方图知,最高的小矩形底边中点的横坐标为=55,即估计得分的众数为55,故C正确;
由0.05+0.35=0.4<0.5,知中位数位于区间[60,70)内,所以中位数的估计值为60+≈63.3,故D错误.故选ABC.
12.BD 解析 10个数据为30,32,34,40,41,45,48,60,78,80,10×0.8=8,故80%分位数为=69,故A错误;
前5天的日均值的极差为41-30=11,后5天的日均值的极差为80-45=35,故B正确;
中位数是=43,故C错误;
根据折线图可知,前5天数据波动性小于后5天数据波动性,故D正确.故选BD.
13.22.6 解析 由表中数据可得a==13.2,
b==9.4,
所以a+b=13.2+9.4=22.6.
14.2 解析 样本a1,a2,a3的方差是2,设其平均数为,则样本2a1+3,2a2+3,2a3+3的平均数为2+3,方差为s2=[(2a1-2)2+(2a2-2)2+(2a3-2)2]=×4[(a1-)2+(a2-)2+(a3-)2]=4×2=8.
故样本2a1+3,2a2+3,2a3+3的标准差为2.
15.17
16.132.25 解析 根据题意,总的样本平均数=168.5,故总的样本方差s2=×[120+(172-168.5)2]+×[120+(165-168.5)2]=132.25.
17.解 (1)由于组距为10,所以有a+0.02+0.025+0.035+a=0.1,从而a=0.01.
(2)平均数为0.1×55+0.2×65+0.35×75+0.25×85+0.1×95=75.5.
(3)第75百分位数为80+×10=84.
能力提升
18.B 解析 不妨设这5个出现的点数为xi∈{1,2,3,4,5,6},i∈{1,2,3,4,5},且x1≤x2≤…≤x5,由题意可知x5=6.
因为这些点数的平均数为2,则xi=2×5=10,可得xi=4,所以xi=1,i∈{1,2,3,4},即这5个数依次为1,1,1,1,6.
可得这些点数的方差为s2=×[(1-2)2+(1-2)2+(1-2)2+(1-2)2+(6-2)2]=4.故选B.
19.AC 解析 由题意得10×(0.004+a+0.022+0.028+0.022+0.018)=1,解得a=0.006,故A正确;
由频率分布直方图知,不低于80分的频率之和为0.22+0.18=0.4,因此估计该中学学生对个性化作业评分不低于80的概率为0.4,故B错误;
受访学生评分在区间[50,60)内的有50×0.006×10=3人,依次记为A1,A2,A3,受访学生评分在区间[40,50)内的有50×0.004×10=2人,依次记为B1,B2,从这5名受访学生中随机抽取2人,所有可能的结果共有10种,因为所抽取2人的评分都在区间[40,50)内的结果有1种,因此2人评分都在区间[40,50)内的概率为,故C正确;
因为0.04+0.06+0.22=0.32,0.04+0.06+0.22+0.28=0.6,所以第40百分位数在区间[70,80)内,设为x,则0.04+0.06+0.22+(x-70)×0.028=0.4,解得x≈72.86,故D错误.故选AC.
20.C 解析 对于A,每天图书借出数的极差为130-80=50,故A错误;
对于B,每天图书借出数的平均数为<105,故B错误;
对于C,数据从小到大排序为80,86,97,101,103,108,121,130,则中位数为=102>101,故C正确;
对于D,前4天平均数为=101,则方差为×[(86-101)2+(108-101)2+(80-101)2+(130-101)2]=389,后4天平均数为=105.5,则方差为×[(103-105.5)2+(97-105.5)2+(101-105.5)2+(121-105.5)2]=84.75,
所以前4天图书借出数的方差大于后4天图书借出数的方差,故D错误.故选C.
21.BD 解析 对于A,如1,2,2,2,2,5的平均数不等于2,2,2,2的平均数,故A错误;对于B,不妨设x2≤x3≤x4≤x5,x2,x3,x4,x5的中位数为,x1,x2,…,x6的中位数为,故B正确;对于C,因为x1是最小值,x6是最大值,所以x1,x2,…,x6的数据波动更大,故C错误;对于D,不妨设x2≤x3≤x4≤x5,则x1≤x2≤x3≤x4≤x5≤x6,所以x5-x2≤x6-x1,故D正确.故选BD.
22.解 (1)(a+0.012 5+0.007 5+2b+2×0.002 5)×20=1,又a=3b,得a=0.015,b=0.005.
(2)前3组的频率和为(0.002 5+0.005+0.012 5)×20=0.4,前4组的频率和为(0.002 5+0.005+0.012 5+0.015)×20=0.7,∴第55百分位数位于区间[60,80)内.
∴估计第55百分位数为60+×20=70.
(3)[60,80),[80,100),[100,120)这三组的频率分别为0.015×20=0.3,0.007 5×20=0.15,0.005×20=0.1,比例为6∶3∶2,则从区间[100,120)内抽取的人数为×11=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024数学学业水平考试专题练
优化集训22 统计
基础巩固
1.用抽签法进行抽样有以下几个步骤:
①将总体中的个体编号;
②把号码写在形状、大小相同的号签上(号签可以用小球、卡片、纸条制作);
③将这些号签放在一个容器内并搅拌均匀;
④从这个容器中逐个不放回地抽取号签,将取出号签所对应的个体作为样本.
这些步骤的先后顺序应为( )
A.①②③④ B.②③④①
C.①③④② D.①④②③
2.下列问题中,最适合用简单随机抽样法抽样的是 ( )
A.某电影院有32排座位,每排有40个座位,座位号是1~40,有一次报告会坐满了听众,报告会结束以后为听取意见,需留下32名听众进行座谈
B.从10台冰箱中抽出3台进行质量检查
C.某学校有在编人员160人,其中行政人员16人,教师112人,后勤人员32人,教育部门为了了解学校机构改革意见,要从中抽取一个容量为20的样本
D.某乡有山地8 000 km2,丘陵12 000 km2,平地24 000 km2,洼地4 000 km2,现抽取480 km2估计全乡农田的平均产量
3.(2023浙江绍兴)某组数据33,36,38,39,42,46,49,49,51,56的第80百分位数为( )
A.46 B.49
C.50 D.51
4.(2023浙江丽水)某中学组织三个年级的学生进行党史知识竞赛.经统计,得到成绩前200名学生分布的扇形图(如图)和成绩前200名中高一学生排名分布的条形图(如图),则下列说法错误的是( )
成绩前200名学生分布的扇形图
成绩前200名中高一学生排名分布的条形图
A.成绩前200名的学生中,高一人数比高二人数多30
B.成绩前100名的学生中,高一人数不超过50
C.成绩前50名的学生中,高三人数不超过32
D.成绩第51名到第100名的学生中,高二人数比高一人数多
5.(2023浙江丽水)某演讲比赛共有9位评委,分别给出某选手的原始评分9.2,9.5,9.6,9.1,9.3,9.0,8.8,9.3,9.7,评定该选手的成绩时,从9个原始评分中去掉1个最高分和1个最低分,得到7个有效评分.这7个有效评分与9个原始评分相比,不变的数字特征是( )
A.极差 B.中位数 C.平均数 D.方差
6.某城市某年1月到10月中每月空气质量为中度污染的天数分别为1,4,7,9,a,b,13,14,15,17,且9≤a≤b≤13.已知样本的中位数为10,则该样本的方差的最小值为( )
A.21.4 B.22.6 C.22.9 D.23.5
7.四名同学各掷骰子5次,记录每次骰子出现的点数并分别对每位同学掷得的点数进行统计处理,在四名同学以下的统计结果中,可以判断出该同学所掷骰子一定没有出现点数1的是( )
A.平均数为4,中位数为5
B.平均数为5,方差为2.4
C.中位数为4,众数为5
D.中位数为4,方差为2.8
8.某学校有男生400人,女生600人.为调查该校全体学生每天睡眠时间,采用分层随机抽样的方法抽取样本,计算得男生每天睡眠时间均值为7.5小时,方差为1,女生每天睡眠时间均值为7小时,方差为0.5.若男、女样本量按比例分配,则可估计总体方差为( )
A.0.45 B.0.62 C.0.7 D.0.76
9.数据30,29,28,27,26,24,23,22的中位数为( )
A.26 B.27 C.26和27 D.26.5
10.(多选)某公司为检测某型号汽车的质量问题,需对三个批次生产的该型号汽车进行检测,三个批次产量分别为100 000辆、150 000辆和250 000辆,公司质监部门计划从中抽取500辆进行检测,则下列说法正确的有( )
A.样本容量为500
B.采用简单随机抽样比分层随机抽样合适
C.应采用分层随机抽样,三个批次的汽车被抽到的概率不相等
D.应采用分层随机抽样,三个批次分别抽取100辆、150辆、250辆
11.(多选)某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在区间[40,90]上,其得分的频率分布直方图如图所示,则下列结论正确的有( )
A.得分在区间[40,60)内的共有40人
B.从这100名参赛者中随机选取1人,其得分在区间[60,80)内的概率为0.5
C.估计得分的众数为55
D.这100名参赛者得分的中位数约为65
12.(多选)(2023浙江奉化)PM2.5的监测值是用来评价环境空气质量的指标之一.划分等级为:PM2.5日均值在35 μg/m3以下,空气质量为一级;PM2.5日均值在35~75 μg/m3,空气质量为二级;PM2.5日均值超过75 μg/m3为超标.如图是某地12月1日至10日PM2.5的日均值(单位:μg/m3)变化的折线图,关于PM2.5日均值的说法正确的有( )
A.这10天的日均值的80%分位数为60
B.前5天的日均值的极差小于后5天的日均值的极差
C.这10天的日均值的中位数为41
D.前5天的日均值的方差小于后5天的日均值的方差
13.某小区2018年至2023年家庭年平均收入X(单位:万元)与年平均支出Y(单位:万元)的统计资料如下表所示:
年份 2018 2019 2020 2021 2022 2023
收入X 11.5 12.1 13 13.4 14.2 15
支出Y 7.8 8.6 9.2 9.8 10.4 10.6
根据统计资料,该小区家庭年平均收入的中位数是a,家庭年平均支出的平均数为b,则a+b= .
14.若样本a1,a2,a3的方差是2,则样本2a1+3,2a2+3,2a3+3的标准差是 .
15.已知一组数据15,17,14,10,15,17,17,16,14,12,则该组数据的众数是 .
16.(2023浙江湖州)已知采用分层随机抽样的方法得到的高三男生、女生各100名学生的身高情况为:男生平均身高为172 cm,方差为120,女生平均身高为165 cm,方差为120,则总的样本方差是 .
17.某校对100名高一学生的某次数学测试成绩进行统计,分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示频率分布直方图.
(1)求图中a的值;
(2)估计该校学生数学成绩的平均数;
(3)估计该校学生数学成绩的第75百分位数.
能力提升
18.(2023浙江台州)抛掷一枚骰子5次,记录每次骰子出现的点数,已知这些点数的平均数为2且出现点数6,则这些点数的方差为( )
A.3.5 B.4 C.4.5 D.5
19.(多选)(2023浙江湖州)某中学为了解大数据提供的个性化作业的质量情况,随机访问50名学生,根据这50名学生对个性化作业的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].则下列说法正确的有( )
A.频率分布直方图中a的值为0.006
B.估计该中学学生对个性化作业的评分不低于80的概率为0.04
C.从评分在区间[40,60)内的受访学生中,随机抽取2人,此2人评分都在区间[40,50)内的概率为
D.受访学生对个性化作业评分的第40百分位数约为72.6
20.(2023浙江余姚)某图书馆统计了某个月前8天纸质图书的借阅情况,整理数据得到如下折线图.根据折线图,下列结论正确的是( )
A.这8天里,每天图书借出数的极差大于50
B.这8天里,每天图书借出数的平均数大于105
C.这8天里,每天图书借出数的中位数大于101
D.前4天图书借出数的方差小于后4天图书借出数的方差
21.(多选)(2023新高考Ⅰ)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则 ( )
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
22.(2023浙江衢州)某学校对该校学生每周零花钱的数额进行了随机调查,现将统计数据按区间[0,20),[20,40),…,[120,140]分组后绘成如图所示的频率分布直方图,已知a=3b.
(1)求频率分布直方图中a,b的值;
(2)估计该校学生每周零花钱的第55百分位数;
(3)若按照各组频率的比例采用分层随机抽样的方法从每周零花钱在区间[60,120)内的学生中抽取11人,求在区间[100,120)内抽取的人数.
优化集训22 统计
基础巩固
1.A 解析 利用抽签法第一步要进行编号,然后做号签,放入容器,最后按照逐个不放回地抽取号签.故这些步骤的先后顺序应为①②③④.故选A.
2.B 解析 根据总体数据特点分别适用哪种抽样特点,选取适当的抽样方法即可.对于A,数量大,不适合;
对于B,从10台冰箱中抽出3台进行质量检查,适合简单随机抽样;
对于C,D,适合分层随机抽样.故选B.
3.C 解析 ∵10×80%=8,∴第80百分位数为×(49+51)=50.故选C.
4.D 解析 由扇形图,成绩前200名的200人中,高一人数比高二人数多200×(45%-30%)=30,故A正确;
由条形图知,成绩前200名中高一学生排名分布在前100和后100的人数相等,因此成绩前100名的学生中,高一人数为200×45%×=45<50,故B正确;
成绩前50名的学生中,高一人数为200×45%×0.2=18,因此高三最多有32人,故C正确;
成绩在第51到100名的学生中,高一人数为200×45%×0.3=27,故高二最多有23人,因此高二人数比高一少,故D错误.
故选D.
5.B
6.B 解析 由题可知,a+b=20,则该组数据的平均数为=10,
方差s2=,
当且仅当a=b=10时,方差最小,且最小值为s2==22.6.
故选B.
7.B 解析 对于A,1,2,5,6,6符合条件,故A错误;
对于B,若平均数为5且出现点数1,则只能为1,6,6,6,6,此时方差为=4,故B正确;
对于C,1,2,4,5,5符合条件,故C错误;
对于D,1,4,4,5,6平均数为×(1+4+4+5+6)=4,方差为×[(1-4)2+(5-4)2+(6-4)2]=2.8,符合条件,故D错误.
故选B.
8.D 解析 由题意计算总体样本平均数为x=0.4×7.5+0.6×7=7.2,故所求总体方差s2=0.4×[1+(7.5-7.2)2]+0.6×[0.5+(7-7.2)2]=0.76.
故选D.
9.D 解析 因为数据为30,29,28,27,26,24,23,22,所以中位数为=26.5.故选D.
10.AD
11.ABC 解析 根据频率和为1,由(a+0.035+0.030+0.020+0.010)×10=1,解得a=0.005,
得分在区间[40,60)内的频率是0.40,得分在区间[40,60)内的有100×0.40=40(人),故A正确;
得分在区间[60,80)内的频率为0.5,可得从这100名参赛者中随机选取一人,得分在区间[60,80)内的概率为0.5,故B正确;
根据频率分布直方图知,最高的小矩形底边中点的横坐标为=55,即估计得分的众数为55,故C正确;
由0.05+0.35=0.4<0.5,知中位数位于区间[60,70)内,所以中位数的估计值为60+≈63.3,故D错误.故选ABC.
12.BD 解析 10个数据为30,32,34,40,41,45,48,60,78,80,10×0.8=8,故80%分位数为=69,故A错误;
前5天的日均值的极差为41-30=11,后5天的日均值的极差为80-45=35,故B正确;
中位数是=43,故C错误;
根据折线图可知,前5天数据波动性小于后5天数据波动性,故D正确.故选BD.
13.22.6 解析 由表中数据可得a==13.2,
b==9.4,
所以a+b=13.2+9.4=22.6.
14.2 解析 样本a1,a2,a3的方差是2,设其平均数为,则样本2a1+3,2a2+3,2a3+3的平均数为2+3,方差为s2=[(2a1-2)2+(2a2-2)2+(2a3-2)2]=×4[(a1-)2+(a2-)2+(a3-)2]=4×2=8.
故样本2a1+3,2a2+3,2a3+3的标准差为2.
15.17
16.132.25 解析 根据题意,总的样本平均数=168.5,故总的样本方差s2=×[120+(172-168.5)2]+×[120+(165-168.5)2]=132.25.
17.解 (1)由于组距为10,所以有a+0.02+0.025+0.035+a=0.1,从而a=0.01.
(2)平均数为0.1×55+0.2×65+0.35×75+0.25×85+0.1×95=75.5.
(3)第75百分位数为80+×10=84.
能力提升
18.B 解析 不妨设这5个出现的点数为xi∈{1,2,3,4,5,6},i∈{1,2,3,4,5},且x1≤x2≤…≤x5,由题意可知x5=6.
因为这些点数的平均数为2,则xi=2×5=10,可得xi=4,所以xi=1,i∈{1,2,3,4},即这5个数依次为1,1,1,1,6.
可得这些点数的方差为s2=×[(1-2)2+(1-2)2+(1-2)2+(1-2)2+(6-2)2]=4.故选B.
19.AC 解析 由题意得10×(0.004+a+0.022+0.028+0.022+0.018)=1,解得a=0.006,故A正确;
由频率分布直方图知,不低于80分的频率之和为0.22+0.18=0.4,因此估计该中学学生对个性化作业评分不低于80的概率为0.4,故B错误;
受访学生评分在区间[50,60)内的有50×0.006×10=3人,依次记为A1,A2,A3,受访学生评分在区间[40,50)内的有50×0.004×10=2人,依次记为B1,B2,从这5名受访学生中随机抽取2人,所有可能的结果共有10种,因为所抽取2人的评分都在区间[40,50)内的结果有1种,因此2人评分都在区间[40,50)内的概率为,故C正确;
因为0.04+0.06+0.22=0.32,0.04+0.06+0.22+0.28=0.6,所以第40百分位数在区间[70,80)内,设为x,则0.04+0.06+0.22+(x-70)×0.028=0.4,解得x≈72.86,故D错误.故选AC.
20.C 解析 对于A,每天图书借出数的极差为130-80=50,故A错误;
对于B,每天图书借出数的平均数为<105,故B错误;
对于C,数据从小到大排序为80,86,97,101,103,108,121,130,则中位数为=102>101,故C正确;
对于D,前4天平均数为=101,则方差为×[(86-101)2+(108-101)2+(80-101)2+(130-101)2]=389,后4天平均数为=105.5,则方差为×[(103-105.5)2+(97-105.5)2+(101-105.5)2+(121-105.5)2]=84.75,
所以前4天图书借出数的方差大于后4天图书借出数的方差,故D错误.故选C.
21.BD 解析 对于A,如1,2,2,2,2,5的平均数不等于2,2,2,2的平均数,故A错误;对于B,不妨设x2≤x3≤x4≤x5,x2,x3,x4,x5的中位数为,x1,x2,…,x6的中位数为,故B正确;对于C,因为x1是最小值,x6是最大值,所以x1,x2,…,x6的数据波动更大,故C错误;对于D,不妨设x2≤x3≤x4≤x5,则x1≤x2≤x3≤x4≤x5≤x6,所以x5-x2≤x6-x1,故D正确.故选BD.
22.解 (1)(a+0.012 5+0.007 5+2b+2×0.002 5)×20=1,又a=3b,得a=0.015,b=0.005.
(2)前3组的频率和为(0.002 5+0.005+0.012 5)×20=0.4,前4组的频率和为(0.002 5+0.005+0.012 5+0.015)×20=0.7,∴第55百分位数位于区间[60,80)内.
∴估计第55百分位数为60+×20=70.
(3)[60,80),[80,100),[100,120)这三组的频率分别为0.015×20=0.3,0.007 5×20=0.15,0.005×20=0.1,比例为6∶3∶2,则从区间[100,120)内抽取的人数为×11=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
