第9章不等式与不等式组复习课件(共19张PPT) 2023-2024学年人教版七年级数学下册
文档属性
| 名称 | 第9章不等式与不等式组复习课件(共19张PPT) 2023-2024学年人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 808.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:24:15 | ||
图片预览




文档简介
(共19张PPT)
不等式与不等式组
初中数学
学 习 目 标
1.复习不等式及其相关概念,结合数轴表示不等式的解;
2.复习巩固不等式的基本性质,熟练求解一元一次不等式;复习巩固 一元一次不等式组;
3.能应用一元一次不等式(组)的知识分析和解决简单的数学问题和 实际问题。
初中数学
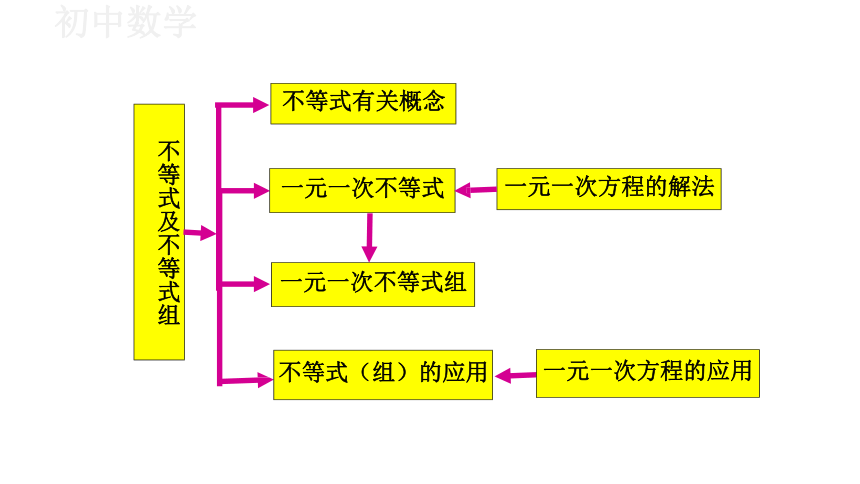
不等式有关概念
不等式及不等式组
一元一次不等式组
不等式(组)的应用
一元一次不等式
一元一次方程的解法
一元一次方程的应用
初中数学
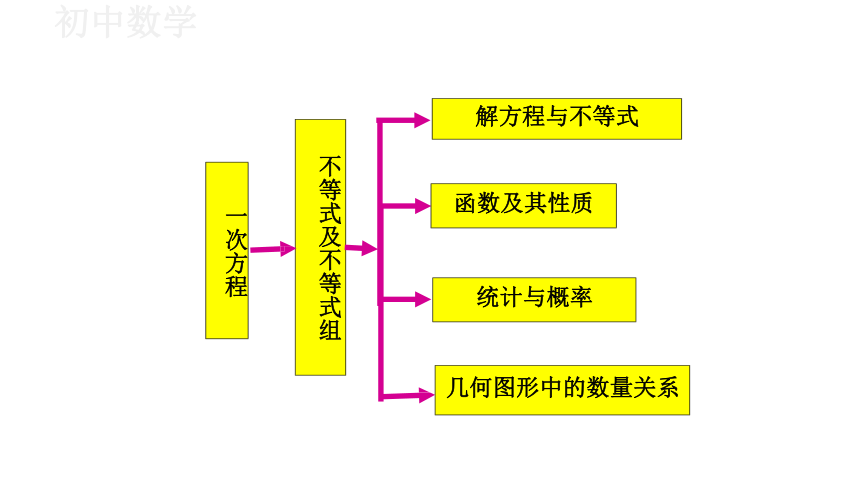
解方程与不等式
不等式及不等式组
统计与概率
几何图形中的数量关系
函数及其性质
一次方程
初中数学
考点一 不等式的有关概念与基本性质
不等式、不等式的解和解集的概念
不等式的基本性质
(1)不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向 不变 . (2)不等式两边同乘(或除以)一个正数,不等号的方向 不变 .
(3)不等式两边同乘(或除以)一个负数,不等号的方向 改变 .
1.用三个不等式a > b , a b > 0 , a < b 中的两个不等式作为题设,余下的一个不等式作为
初中数学
中考命题点1不等式的性质
结论组成一个命题,组成真命题的个数为 ( D )
A.0 B.1 C.2
D.3
1 1
初中数学
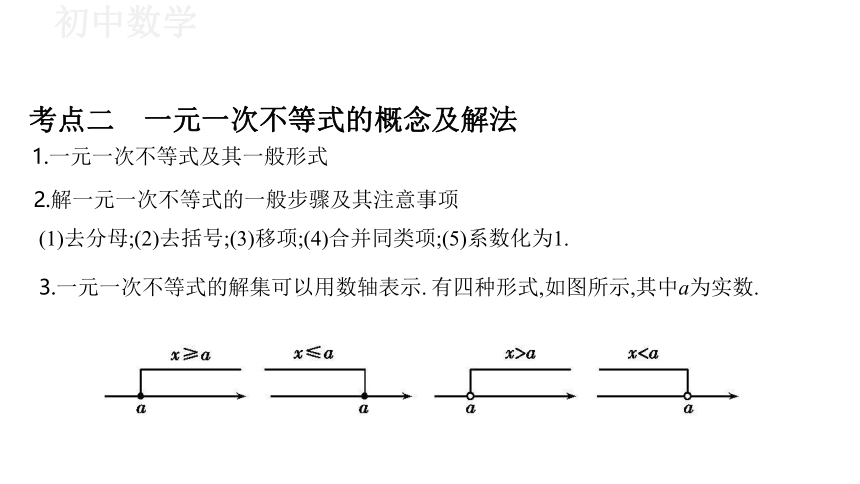
考点二 一元一次不等式的概念及解法
一元一次不等式及其一般形式
解一元一次不等式的一般步骤及其注意事项
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
一元一次不等式的解集可以用数轴表示. 有四种形式,如图所示,其中a为实数.
初中数学
1. 解不等式3(x-1)≤
,并把它的解集在数轴上表示出来.
2
x 4
解析 去分母,得6(x-1)≤x+4, 去括号,得6x-6≤x+4,
移项、合并同类项,得5x≤10, 系数化为1,得x≤2.
将解集表示在数轴上如图.
中考命题点2不等式(组)的解集及数轴表示
讲授新课
2.把不等式组 两个不等式的解集在数轴上表示出来,正确的是
初中数学
答案 C
由不等式①可得x≥-3,由不等式②可得x<1.故选C.
2
x 1
1 x 4,①
1,②
中考命题点2不等式(组)的解集及数轴表示
2
x 1
1 x 4,①
1,②
初中数学
考点三 一元一次不等式组的概念及解法
一元一次不等式组及其解集:
解一元一次不等式组的一般步骤:
(1)求出不等式组中各个不等式的解集; (2)把各不等式的解集表示在数轴上;
(3)在数轴上找出各不等式解集的公共部分,则得到不等式组的解集.
初中数学
中考命题点3不等式(组)的解法
1.解不等式组:
3
x 7
4(x 1) x 2,①
x.②
2
解不等式②,得x 7
解析:解不等式①,得x<2
∴原不等式组的解集为x<2.
∴不等式组的解集为-22
2.解不等式组:
3( x 1) x 1, ①
x 9 2 x, ②
解析 :由①得2x>-4,解得x>-2,
由②得-3x>-9,解得x<3.
初中数学
中考命题点3不等式(组)的解法
初中数学
考点四 一元一次不等式的应用
列不等式(组)解决实际问题,要注意抓住问题中的一些关键词语,如“至少”、
“最多”等。另外,对一些实际问题的分析,还要注意结合实际情况。
列不等式解应用题的一般步骤:
(1)审题;(2)设未知数;(3)找出能够包含未知数的不等量关系,列出不等式;
(4)求出不等式的解;(5)在不等式(组)的解中找出符合题意的值;(6)写出答案
(包括单位名称)。
初中数学
中考命题点4不等式的应用
1.某工厂为贯彻落实“绿水青山就是金山银山”的发展理念,投资组建了日废水处理量为m吨的废水处 理车间,对该厂工业废水进行无害化处理.但随着工厂生产规模的扩大,该车间经常无法完成当天工业废 水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理.已知该车间处理废水,每天需固定 成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记 录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.
求该车间的日废水处理量m;
为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过 10元/吨,试计算该厂一天产生的工业废水量的范围.
初中数学
中考命题点4不等式的应用
(1) ∵工厂产生工业废水35吨,共花费废水处理费370元,
又∵
= >8,
∴ m<35,
依题意得 30+8m+12(35-m)=370,
解得m=20.
故该车间的日废水处理量为20吨.
35
370 30 68
7
易错警示 在解第(1)问时,要判断m与35的大小关系.
初中数学
中考命题点4不等式的应用
(2)设该厂一天产生的工业废水量为x吨.
①当0②当x>20时,依题意得,12(x-20)+20×8+30≤10x, 解得x≤25, ∴ 20综上所述,15≤x≤25.
答:该厂一天产生的工业废水量的范围在15吨到25吨之间.
易错警示 在解第(2)问时,要考虑到0初中数学
中考命题点4不等式的应用
(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的 .请设计
2.学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品 共需120元;购买5个A奖品和4个B奖品共需210元.
(1)求A,B两种奖品的单价;
1
3
出最省钱的购买方案,并说明理由.
解:(1)设A奖品的单价为x元,B奖品的单价为y元,
所以A奖品的单价为30元,B奖品的单价为15元.
根据题意,得
3x 2 y 120, x 30,
解得
5x 4 y 210. y 15.
初中数学
中考命题点4不等式的应用
(2)设购买A奖品a个,则购买B奖品(30-a)个,共需w元,
根据题意,得w=30a+15(30-a)=15a+450.
∵15>0,∴当a取最小值时,w有最小值.
1
由a≥ 3 (30-a),解得a≥7.5.
而a为正整数,∴当a=8时,w取得最小值,此时30-8=22. 所以当购买A奖品8个,B奖品22个时最省钱.
初中数学
课 堂 小 结
不等式相关概念
不等式与不等式组的解法
利用不等式或不等式组解决实际问题
不等式与不等式组
初中数学
学 习 目 标
1.复习不等式及其相关概念,结合数轴表示不等式的解;
2.复习巩固不等式的基本性质,熟练求解一元一次不等式;复习巩固 一元一次不等式组;
3.能应用一元一次不等式(组)的知识分析和解决简单的数学问题和 实际问题。
初中数学
不等式有关概念
不等式及不等式组
一元一次不等式组
不等式(组)的应用
一元一次不等式
一元一次方程的解法
一元一次方程的应用
初中数学
解方程与不等式
不等式及不等式组
统计与概率
几何图形中的数量关系
函数及其性质
一次方程
初中数学
考点一 不等式的有关概念与基本性质
不等式、不等式的解和解集的概念
不等式的基本性质
(1)不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向 不变 . (2)不等式两边同乘(或除以)一个正数,不等号的方向 不变 .
(3)不等式两边同乘(或除以)一个负数,不等号的方向 改变 .
1.用三个不等式a > b , a b > 0 , a < b 中的两个不等式作为题设,余下的一个不等式作为
初中数学
中考命题点1不等式的性质
结论组成一个命题,组成真命题的个数为 ( D )
A.0 B.1 C.2
D.3
1 1
初中数学
考点二 一元一次不等式的概念及解法
一元一次不等式及其一般形式
解一元一次不等式的一般步骤及其注意事项
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
一元一次不等式的解集可以用数轴表示. 有四种形式,如图所示,其中a为实数.
初中数学
1. 解不等式3(x-1)≤
,并把它的解集在数轴上表示出来.
2
x 4
解析 去分母,得6(x-1)≤x+4, 去括号,得6x-6≤x+4,
移项、合并同类项,得5x≤10, 系数化为1,得x≤2.
将解集表示在数轴上如图.
中考命题点2不等式(组)的解集及数轴表示
讲授新课
2.把不等式组 两个不等式的解集在数轴上表示出来,正确的是
初中数学
答案 C
由不等式①可得x≥-3,由不等式②可得x<1.故选C.
2
x 1
1 x 4,①
1,②
中考命题点2不等式(组)的解集及数轴表示
2
x 1
1 x 4,①
1,②
初中数学
考点三 一元一次不等式组的概念及解法
一元一次不等式组及其解集:
解一元一次不等式组的一般步骤:
(1)求出不等式组中各个不等式的解集; (2)把各不等式的解集表示在数轴上;
(3)在数轴上找出各不等式解集的公共部分,则得到不等式组的解集.
初中数学
中考命题点3不等式(组)的解法
1.解不等式组:
3
x 7
4(x 1) x 2,①
x.②
2
解不等式②,得x 7
解析:解不等式①,得x<2
∴原不等式组的解集为x<2.
∴不等式组的解集为-2
2.解不等式组:
3( x 1) x 1, ①
x 9 2 x, ②
解析 :由①得2x>-4,解得x>-2,
由②得-3x>-9,解得x<3.
初中数学
中考命题点3不等式(组)的解法
初中数学
考点四 一元一次不等式的应用
列不等式(组)解决实际问题,要注意抓住问题中的一些关键词语,如“至少”、
“最多”等。另外,对一些实际问题的分析,还要注意结合实际情况。
列不等式解应用题的一般步骤:
(1)审题;(2)设未知数;(3)找出能够包含未知数的不等量关系,列出不等式;
(4)求出不等式的解;(5)在不等式(组)的解中找出符合题意的值;(6)写出答案
(包括单位名称)。
初中数学
中考命题点4不等式的应用
1.某工厂为贯彻落实“绿水青山就是金山银山”的发展理念,投资组建了日废水处理量为m吨的废水处 理车间,对该厂工业废水进行无害化处理.但随着工厂生产规模的扩大,该车间经常无法完成当天工业废 水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理.已知该车间处理废水,每天需固定 成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记 录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.
求该车间的日废水处理量m;
为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过 10元/吨,试计算该厂一天产生的工业废水量的范围.
初中数学
中考命题点4不等式的应用
(1) ∵工厂产生工业废水35吨,共花费废水处理费370元,
又∵
= >8,
∴ m<35,
依题意得 30+8m+12(35-m)=370,
解得m=20.
故该车间的日废水处理量为20吨.
35
370 30 68
7
易错警示 在解第(1)问时,要判断m与35的大小关系.
初中数学
中考命题点4不等式的应用
(2)设该厂一天产生的工业废水量为x吨.
①当0
答:该厂一天产生的工业废水量的范围在15吨到25吨之间.
易错警示 在解第(2)问时,要考虑到0
中考命题点4不等式的应用
(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的 .请设计
2.学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品 共需120元;购买5个A奖品和4个B奖品共需210元.
(1)求A,B两种奖品的单价;
1
3
出最省钱的购买方案,并说明理由.
解:(1)设A奖品的单价为x元,B奖品的单价为y元,
所以A奖品的单价为30元,B奖品的单价为15元.
根据题意,得
3x 2 y 120, x 30,
解得
5x 4 y 210. y 15.
初中数学
中考命题点4不等式的应用
(2)设购买A奖品a个,则购买B奖品(30-a)个,共需w元,
根据题意,得w=30a+15(30-a)=15a+450.
∵15>0,∴当a取最小值时,w有最小值.
1
由a≥ 3 (30-a),解得a≥7.5.
而a为正整数,∴当a=8时,w取得最小值,此时30-8=22. 所以当购买A奖品8个,B奖品22个时最省钱.
初中数学
课 堂 小 结
不等式相关概念
不等式与不等式组的解法
利用不等式或不等式组解决实际问题
