圆的创新作图课件(共20张PPT)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 圆的创新作图课件(共20张PPT)2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
创 新 作 图
初中数学
学 习 目 标
1.熟练掌握图形变化的性质和一些基本图形的特征;
2.通过对图形的观察、操作和想象,进而进行推理、实验和归纳,培 养分析问题和解决问题的能力;
3.渗透“转化”的数学思想,感受数学之美.
初中数学
问题情境引入
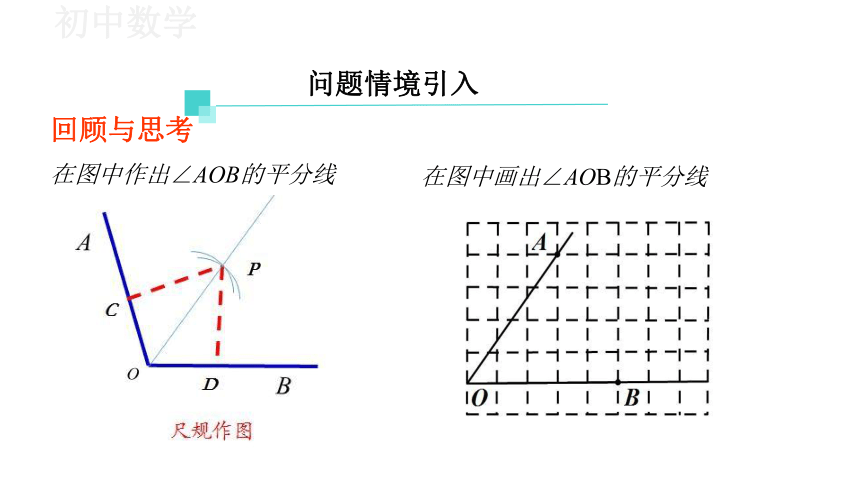
回顾与思考
在图中作出∠AOB的平分线
在图中画出∠AOB的平分线
初中数学
创新作图题是在一定情境下,以无刻度的直尺作为唯一的作图工具,
综合运用图形的性质、基本定理、图形变换等进行分析、推理和归纳, 寻找作图依据,主要形式是找点和连线。它是在传统的尺规作图的基础 上,保留了尺规作图严密的逻辑推理要求,结合几何推理,对所要作的 图形进行作图原理和作图方法的探索.
初中数学
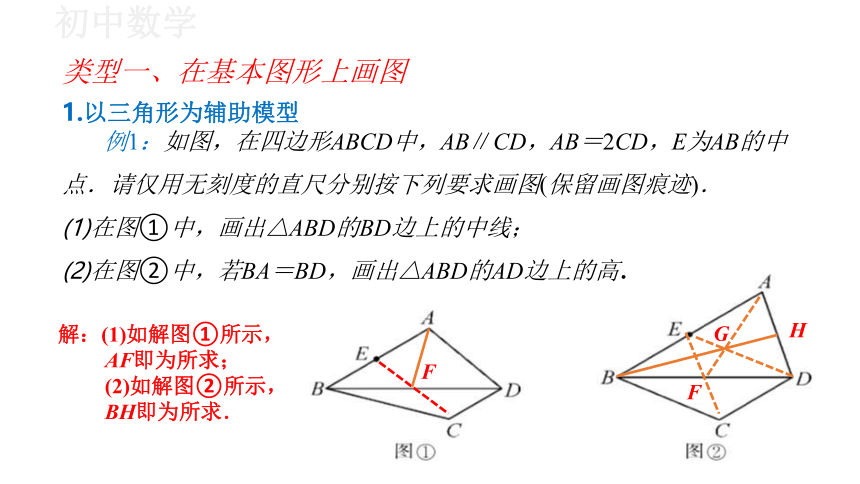
解:(1)如解图①所示,
AF即为所求;
(2)如解图②所示,
BH即为所求.
F
F
G
H
类型一、在基本图形上画图
1.以三角形为辅助模型
例1:如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中
点.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
在图①中,画出△ABD的BD边上的中线;
在图②中,若BA=BD,画出△ABD的AD边上的高.
初中数学
新 知 讲 解
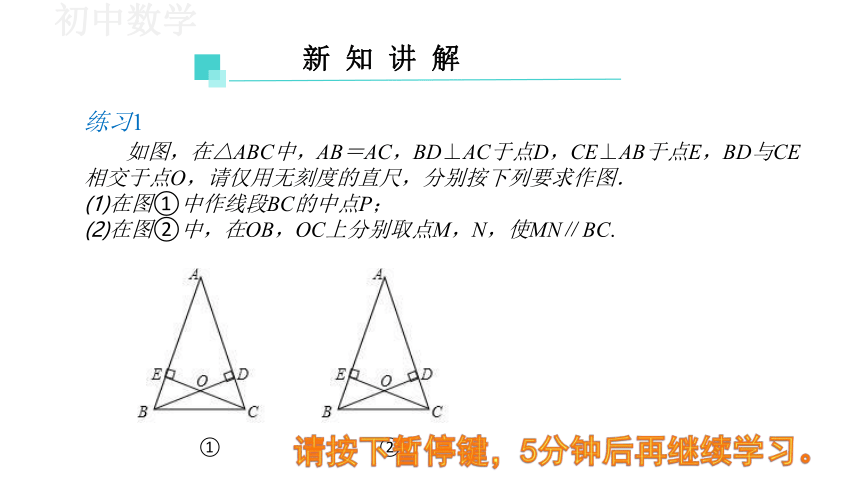
练习1
如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE 相交于点O,请仅用无刻度的直尺,分别按下列要求作图.
在图①中作线段BC的中点P;
在图②中,在OB,OC上分别取点M,N,使MN∥BC.
①
②
初中数学
①
②
初中数学
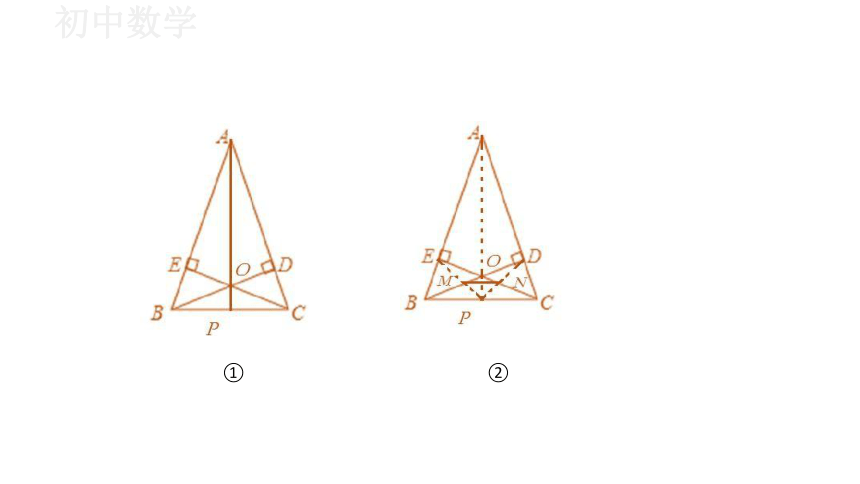
解决与三角形有关的创新画(作)图问题时,一定要注意三角 形的基本性质,如三条高线、三条中线、三条角平分线交于一点;三 角形的中位线平行于第三边并且等于第三边的一半;三角形的中线平 分三角形面积等.由于创新作图题只要求用无刻度的直尺作图,因此 找点很重要,而一般情况下,所找的点都是与三角形三边有关的特殊 点,如边的中点;三角形内心、重心等.
初中数学
O
A
B
C
解:如图所示,射线OC即为所求.
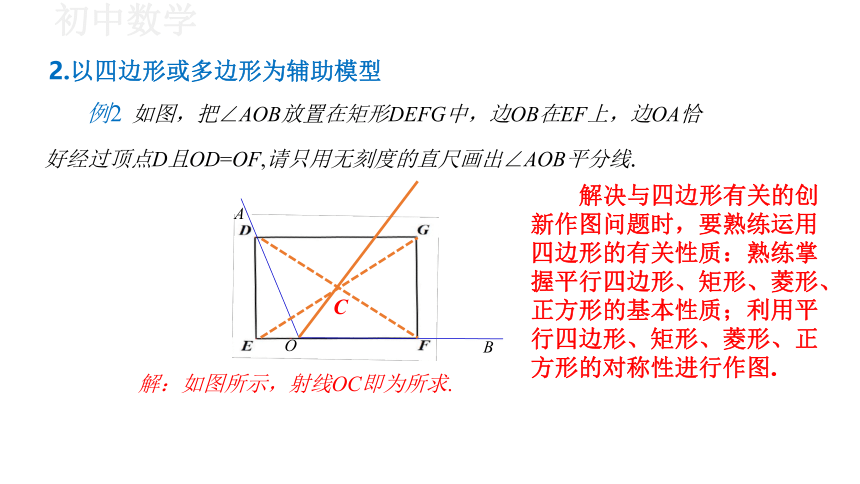
2.以四边形或多边形为辅助模型
例2 如图,把∠AOB放置在矩形DEFG中,边OB在EF上,边OA恰 好经过顶点D且OD=OF,请只用无刻度的直尺画出∠AOB平分线.
解决与四边形有关的创 新作图问题时,要熟练运用 四边形的有关性质:熟练掌 握平行四边形、矩形、菱形、 正方形的基本性质;利用平 行四边形、矩形、菱形、正 方形的对称性进行作图.
初中数学
练习2 如图,在菱形ABCD中,点E为AB的中点,请只用无刻 度的直尺作图.
如图1,在CD上找点F,使点F是CD的中点;
如图2,在AD上找点G,使点G是AD的中点.
初中数学
练习2 在菱形ABCD中,点E为AB的中 点,请只用无刻度的直尺作图.
如图1,在CD上找点F,使点F是CD的中点;
如图2,在AD上找点G,使点G是AD的中点.
解(1)如图1所示,F点即所求
(2)如图2所示,G点即所求
在图(2)中作一条与AD边平行的弦
.
本题考查切线的性质、平行 四边形的性质、垂径定理等知识, 解题的关键是从结论出发逆推不 断寻找条件.
3.以圆为辅助模型
例3 如图, ABCD的顶点A、B、D均在⊙O上,请仅用无刻度的直尺按要求作图。
(1)AB边经过圆心O,在图(1)中作一条与AD边平行的直径;
(2):A(B边1)不连经接过A圆C、心BOD,交D于C与点⊙K,O相过切点于O、点KD,
(1)作直径EF, EF为所求.
(2)连接OD,DO的延长线交AB于T,连接AC、
BD交于K,过T、K作弦GH,GH为所求.
初中数学
练习3 在⊙O中,点D是劣弧AB的中点,仅用无刻度的直尺画线的 方法,按要求完成下列作图:
在图①中作出∠C的平分线;
在图②中画一条弦,平分△ABC的面积.
初中数学
练习3 在⊙O中,点D是劣弧AB的中点,仅用无刻度的直尺画线的 方法,按要求完成下列作图:
在图①中作出∠C的平分线;
在图②中画一条弦,平分△ABC的面积.
解:如图,CD、CE为所作;
在圆中画图应立足圆的对称 性、垂径定理及推论等性质,借 助圆心角、圆周角、弧之间的关 系和切线的性质等构建有关的点、 线、图形之间的特征、形状、位 置和大小关系.
初中数学
新 知 讲 解
类型二、在网格上画图
例4 在10×10的正方形网格中(每个小正方形的边长为1),线段AB在网格中 的位置如图所示.请仅用无刻度直尺,按要求分别完成以下画图.
(1)在图①中,画出一个以AB为边,另两个顶点C,D也在格点上的菱形ABCD. (2)在图②中,画出一个以A,B为顶点,另两个顶点C,D也在格点上的菱形, 且使这个菱形的面积最大或最小(仅选其一即可).其面积值是 .
初中数学
解:(1)以AB为边,另两个顶点C,D也在格点上的菱形ABCD有多种画 法,如下图所示.
初中数学
面积最大为15,最小为5.
及大小.
(2)在图②中,画出一个以A,B为顶点,另两个顶点C,D也在格点上的菱形, 且使这个菱形的面积最大或最小(仅选其一即可).其面积值是 .
解:(2)以A,B为顶点,另两个顶点C,D也在格点上的菱形,且 使这个菱形的面积最大或最小的图形如下:
以网格或坐标为背景画
图,关键是把握网格或坐标 特征:各格点之间的距离可 能为正整数,也可能为无理 数,借助勾股定理的逆定理 构建直角三角形等,酝酿与 构建相关图形的形状、位置
初中数学
练习4 如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半 径为 10 .规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三 角形”,请仅用无刻度的直尺,分别按照下列条件,在图(1),图(2)中 画一个“圆格三角形”.
3
(1)一个锐角的正切值为1;
(2)面积为8.
图(1)
图(2)
初中数学
A
B
C
D
F
E
解:(1)如图①,△ABC即为所求.(画法不唯一)
(2)如图②,△DEF即为所求.(画法不唯一)
图①
图②
初中数学
课 堂 小 结
1.复习了基本图形的性质,进一步熟悉图形变换的特征;
2.通过对图形的观察、操作和想象,进而进行推理、实验和归纳, 提升了分析问题和解决问题的能力;
3.通过不断深化“转化” 的数学思想,感受了数学之美.
创 新 作 图
初中数学
学 习 目 标
1.熟练掌握图形变化的性质和一些基本图形的特征;
2.通过对图形的观察、操作和想象,进而进行推理、实验和归纳,培 养分析问题和解决问题的能力;
3.渗透“转化”的数学思想,感受数学之美.
初中数学
问题情境引入
回顾与思考
在图中作出∠AOB的平分线
在图中画出∠AOB的平分线
初中数学
创新作图题是在一定情境下,以无刻度的直尺作为唯一的作图工具,
综合运用图形的性质、基本定理、图形变换等进行分析、推理和归纳, 寻找作图依据,主要形式是找点和连线。它是在传统的尺规作图的基础 上,保留了尺规作图严密的逻辑推理要求,结合几何推理,对所要作的 图形进行作图原理和作图方法的探索.
初中数学
解:(1)如解图①所示,
AF即为所求;
(2)如解图②所示,
BH即为所求.
F
F
G
H
类型一、在基本图形上画图
1.以三角形为辅助模型
例1:如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中
点.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
在图①中,画出△ABD的BD边上的中线;
在图②中,若BA=BD,画出△ABD的AD边上的高.
初中数学
新 知 讲 解
练习1
如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE 相交于点O,请仅用无刻度的直尺,分别按下列要求作图.
在图①中作线段BC的中点P;
在图②中,在OB,OC上分别取点M,N,使MN∥BC.
①
②
初中数学
①
②
初中数学
解决与三角形有关的创新画(作)图问题时,一定要注意三角 形的基本性质,如三条高线、三条中线、三条角平分线交于一点;三 角形的中位线平行于第三边并且等于第三边的一半;三角形的中线平 分三角形面积等.由于创新作图题只要求用无刻度的直尺作图,因此 找点很重要,而一般情况下,所找的点都是与三角形三边有关的特殊 点,如边的中点;三角形内心、重心等.
初中数学
O
A
B
C
解:如图所示,射线OC即为所求.
2.以四边形或多边形为辅助模型
例2 如图,把∠AOB放置在矩形DEFG中,边OB在EF上,边OA恰 好经过顶点D且OD=OF,请只用无刻度的直尺画出∠AOB平分线.
解决与四边形有关的创 新作图问题时,要熟练运用 四边形的有关性质:熟练掌 握平行四边形、矩形、菱形、 正方形的基本性质;利用平 行四边形、矩形、菱形、正 方形的对称性进行作图.
初中数学
练习2 如图,在菱形ABCD中,点E为AB的中点,请只用无刻 度的直尺作图.
如图1,在CD上找点F,使点F是CD的中点;
如图2,在AD上找点G,使点G是AD的中点.
初中数学
练习2 在菱形ABCD中,点E为AB的中 点,请只用无刻度的直尺作图.
如图1,在CD上找点F,使点F是CD的中点;
如图2,在AD上找点G,使点G是AD的中点.
解(1)如图1所示,F点即所求
(2)如图2所示,G点即所求
在图(2)中作一条与AD边平行的弦
.
本题考查切线的性质、平行 四边形的性质、垂径定理等知识, 解题的关键是从结论出发逆推不 断寻找条件.
3.以圆为辅助模型
例3 如图, ABCD的顶点A、B、D均在⊙O上,请仅用无刻度的直尺按要求作图。
(1)AB边经过圆心O,在图(1)中作一条与AD边平行的直径;
(2):A(B边1)不连经接过A圆C、心BOD,交D于C与点⊙K,O相过切点于O、点KD,
(1)作直径EF, EF为所求.
(2)连接OD,DO的延长线交AB于T,连接AC、
BD交于K,过T、K作弦GH,GH为所求.
初中数学
练习3 在⊙O中,点D是劣弧AB的中点,仅用无刻度的直尺画线的 方法,按要求完成下列作图:
在图①中作出∠C的平分线;
在图②中画一条弦,平分△ABC的面积.
初中数学
练习3 在⊙O中,点D是劣弧AB的中点,仅用无刻度的直尺画线的 方法,按要求完成下列作图:
在图①中作出∠C的平分线;
在图②中画一条弦,平分△ABC的面积.
解:如图,CD、CE为所作;
在圆中画图应立足圆的对称 性、垂径定理及推论等性质,借 助圆心角、圆周角、弧之间的关 系和切线的性质等构建有关的点、 线、图形之间的特征、形状、位 置和大小关系.
初中数学
新 知 讲 解
类型二、在网格上画图
例4 在10×10的正方形网格中(每个小正方形的边长为1),线段AB在网格中 的位置如图所示.请仅用无刻度直尺,按要求分别完成以下画图.
(1)在图①中,画出一个以AB为边,另两个顶点C,D也在格点上的菱形ABCD. (2)在图②中,画出一个以A,B为顶点,另两个顶点C,D也在格点上的菱形, 且使这个菱形的面积最大或最小(仅选其一即可).其面积值是 .
初中数学
解:(1)以AB为边,另两个顶点C,D也在格点上的菱形ABCD有多种画 法,如下图所示.
初中数学
面积最大为15,最小为5.
及大小.
(2)在图②中,画出一个以A,B为顶点,另两个顶点C,D也在格点上的菱形, 且使这个菱形的面积最大或最小(仅选其一即可).其面积值是 .
解:(2)以A,B为顶点,另两个顶点C,D也在格点上的菱形,且 使这个菱形的面积最大或最小的图形如下:
以网格或坐标为背景画
图,关键是把握网格或坐标 特征:各格点之间的距离可 能为正整数,也可能为无理 数,借助勾股定理的逆定理 构建直角三角形等,酝酿与 构建相关图形的形状、位置
初中数学
练习4 如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半 径为 10 .规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三 角形”,请仅用无刻度的直尺,分别按照下列条件,在图(1),图(2)中 画一个“圆格三角形”.
3
(1)一个锐角的正切值为1;
(2)面积为8.
图(1)
图(2)
初中数学
A
B
C
D
F
E
解:(1)如图①,△ABC即为所求.(画法不唯一)
(2)如图②,△DEF即为所求.(画法不唯一)
图①
图②
初中数学
课 堂 小 结
1.复习了基本图形的性质,进一步熟悉图形变换的特征;
2.通过对图形的观察、操作和想象,进而进行推理、实验和归纳, 提升了分析问题和解决问题的能力;
3.通过不断深化“转化” 的数学思想,感受了数学之美.
同课章节目录
