角的大小比较(安徽省淮北市烈山区马桥中学)
文档属性
| 名称 | 角的大小比较(安徽省淮北市烈山区马桥中学) |

|
|
| 格式 | rar | ||
| 文件大小 | 120.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-09 00:00:00 | ||
图片预览


文档简介
课件15张PPT。角的大小比较授课人:董晨曦导入 观察与思考:
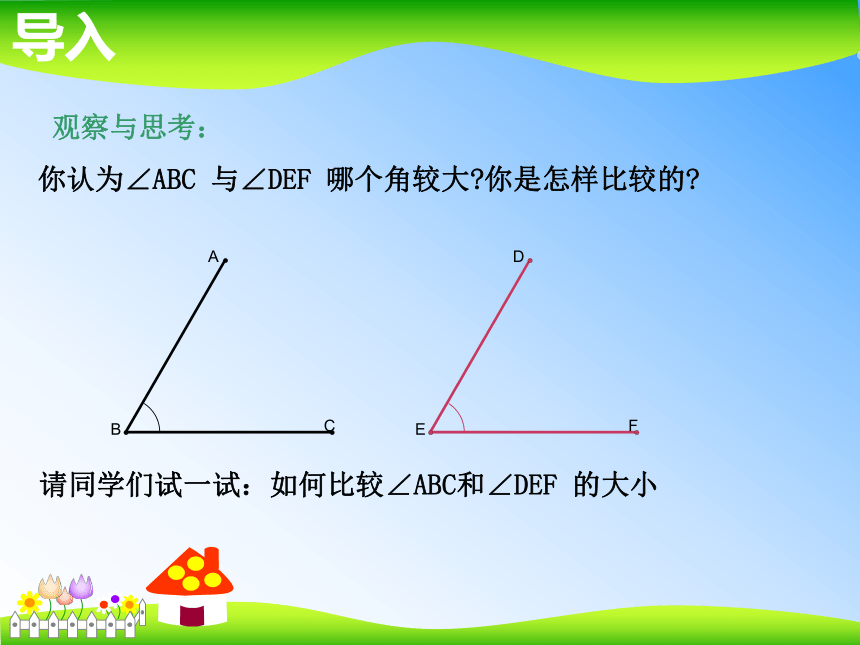
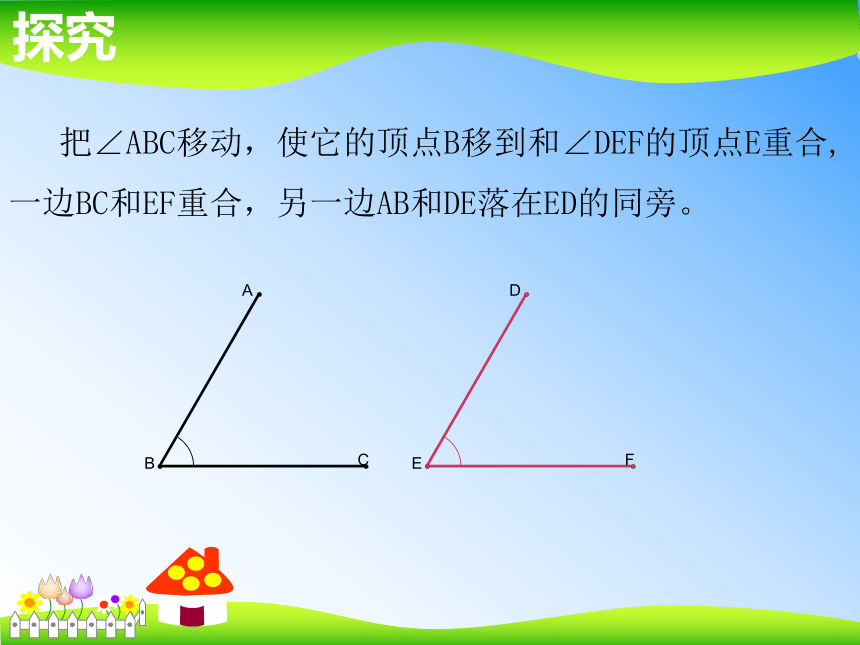
你认为∠ABC 与∠DEF 哪个角较大?你是怎样比较的?请同学们试一试:如何比较∠ABC和∠DEF 的大小 把∠ABC移动,使它的顶点B移到和∠DEF的顶点E重合,
一边BC和EF重合,另一边AB和DE落在ED的同旁。探究(1)如果AB与ED重合,那么∠ABC就等于∠DEF,记作
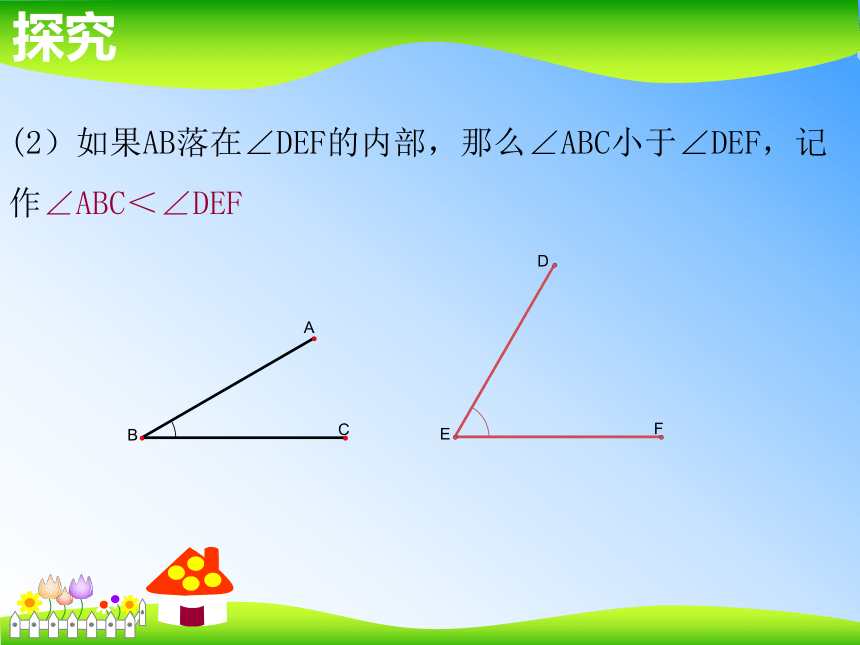
∠ABC=∠DEF探究(2)如果AB落在∠DEF的内部,那么∠ABC小于∠DEF,记
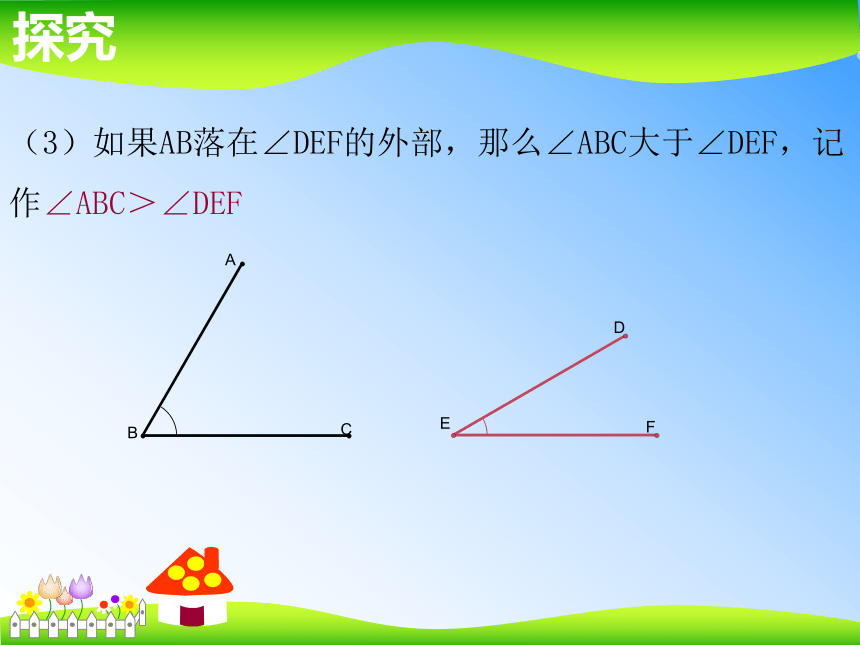
作∠ABC<∠DEF探究(3)如果AB落在∠DEF的外部,那么∠ABC大于∠DEF,记
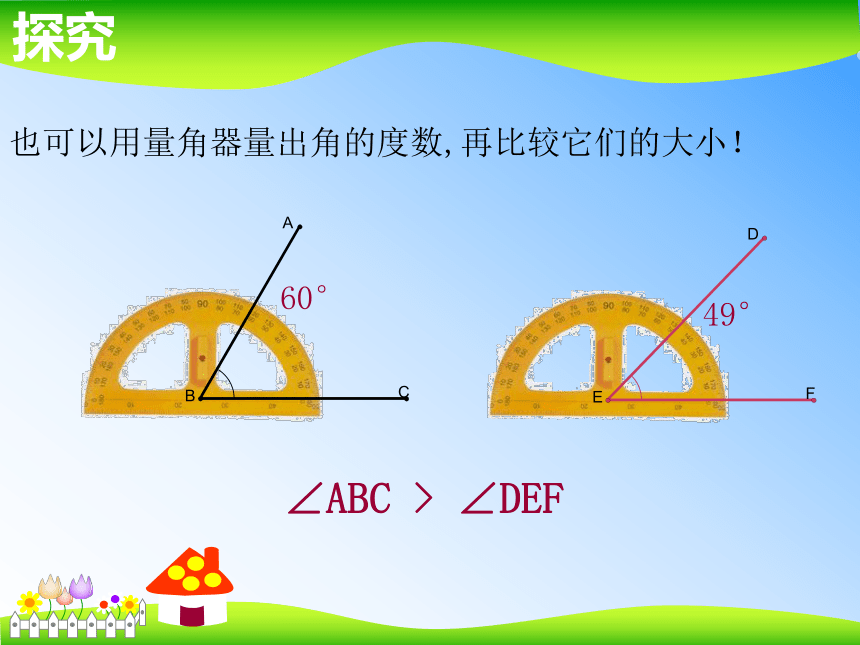
作∠ABC>∠DEF探究也可以用量角器量出角的度数,再比较它们的大小!60°49°∠ABC > ∠DEF探究 以上我们用了两种方法比较两个角的大小,你能给它们起个名字吗?除此之外,我们还有其它方法吗?
度量法叠合法思维发展 图中的∠AOB,∠COB,∠AOB。如何表示它们之间的关系. 和关系: 差关系:∠AOB=∠COB+∠COB
∠BOC=∠AOB-∠AOC
∠AOC=∠AOB-∠BOCOB在∠AOC内例1 如图,求解下列问题:
(1)比较∠AOC与∠BOC,∠BOD与∠COD的大小。
(2)将∠AOC写成两个角的和与两个角的差的形式。解: (1) 由图可知:
∠AOC > ∠BOC ∠BOD > ∠COD(OC在∠BOD内)(2)∠AOC= ∠AOB + ∠BOC∠AOC= ∠AOD - ∠COD解析 在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线。如图: OC是∠AOB的角平分线,这时有:∠AOC=∠COB = ∠AOB或∠AOB=2∠AOC= 2∠COB
归纳
例2:已知 OB是∠AOC的平分线,OD是∠COE的平分线。
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB是多少度?30°30°40°40°提高∠ABC= ∠ABD+ ∠_____;
∠ADB= ∠ADC- ∠_____。2、如图:如果BD是∠ABC的平分线,那么:(1)∠ABD = ∠_____;(2)∠___ =2∠ DBC。1、如图:填空CBDCDBCBDABC练习小结再见
你认为∠ABC 与∠DEF 哪个角较大?你是怎样比较的?请同学们试一试:如何比较∠ABC和∠DEF 的大小 把∠ABC移动,使它的顶点B移到和∠DEF的顶点E重合,
一边BC和EF重合,另一边AB和DE落在ED的同旁。探究(1)如果AB与ED重合,那么∠ABC就等于∠DEF,记作
∠ABC=∠DEF探究(2)如果AB落在∠DEF的内部,那么∠ABC小于∠DEF,记
作∠ABC<∠DEF探究(3)如果AB落在∠DEF的外部,那么∠ABC大于∠DEF,记
作∠ABC>∠DEF探究也可以用量角器量出角的度数,再比较它们的大小!60°49°∠ABC > ∠DEF探究 以上我们用了两种方法比较两个角的大小,你能给它们起个名字吗?除此之外,我们还有其它方法吗?
度量法叠合法思维发展 图中的∠AOB,∠COB,∠AOB。如何表示它们之间的关系. 和关系: 差关系:∠AOB=∠COB+∠COB
∠BOC=∠AOB-∠AOC
∠AOC=∠AOB-∠BOCOB在∠AOC内例1 如图,求解下列问题:
(1)比较∠AOC与∠BOC,∠BOD与∠COD的大小。
(2)将∠AOC写成两个角的和与两个角的差的形式。解: (1) 由图可知:
∠AOC > ∠BOC ∠BOD > ∠COD(OC在∠BOD内)(2)∠AOC= ∠AOB + ∠BOC∠AOC= ∠AOD - ∠COD解析 在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线。如图: OC是∠AOB的角平分线,这时有:∠AOC=∠COB = ∠AOB或∠AOB=2∠AOC= 2∠COB
归纳
例2:已知 OB是∠AOC的平分线,OD是∠COE的平分线。
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB是多少度?30°30°40°40°提高∠ABC= ∠ABD+ ∠_____;
∠ADB= ∠ADC- ∠_____。2、如图:如果BD是∠ABC的平分线,那么:(1)∠ABD = ∠_____;(2)∠___ =2∠ DBC。1、如图:填空CBDCDBCBDABC练习小结再见
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
