18.2.1 矩 形 课件(共36张PPT) 人教版八年级数学 下册
文档属性
| 名称 | 18.2.1 矩 形 课件(共36张PPT) 人教版八年级数学 下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 570.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 12:50:47 | ||
图片预览





文档简介
(共36张PPT)
八年级数学·下 新课标[人]
第十八章 平行四边形
18.2.1 矩 形(第1课时)
一个活动的平行四边形教具,轻轻拉动一个点,不管怎么拉,它还是一个平行四边形吗 为什么
有一个角是直角的平行四边形叫做矩形,也就是长方形.
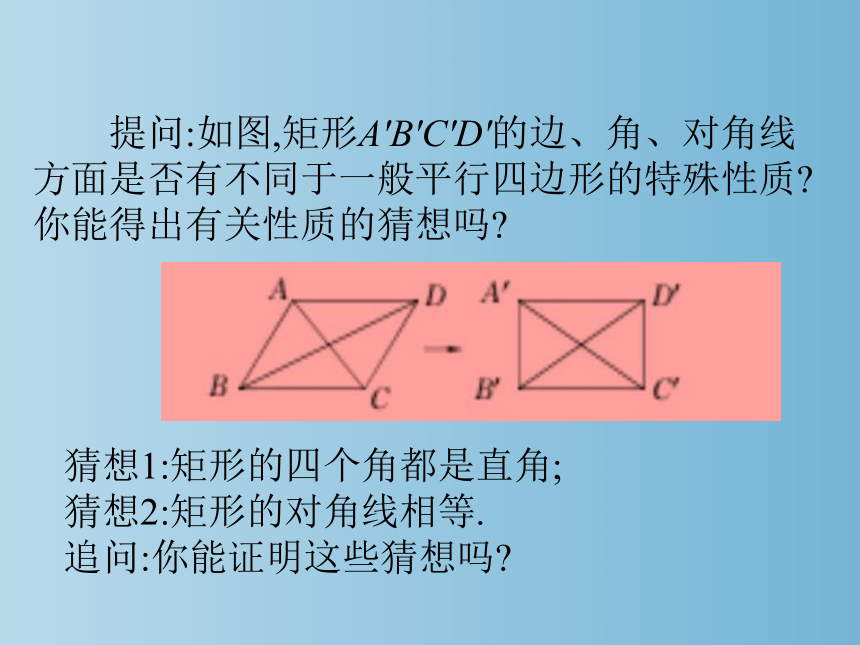
提问:如图,矩形A'B'C'D'的边、角、对角线方面是否有不同于一般平行四边形的特殊性质 你能得出有关性质的猜想吗
猜想1:矩形的四个角都是直角;
猜想2:矩形的对角线相等.
追问:你能证明这些猜想吗
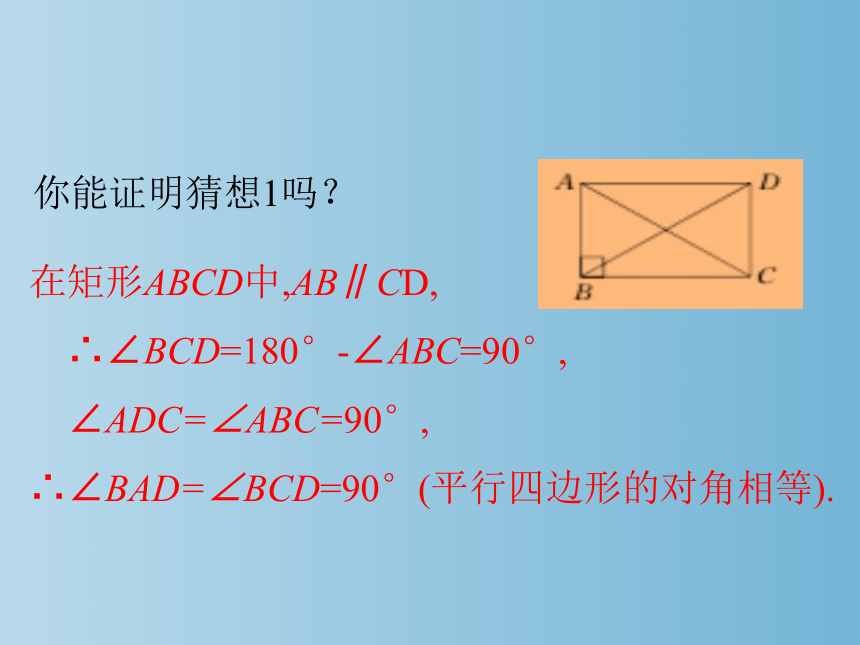
你能证明猜想1吗?
在矩形ABCD中,AB∥CD,
∴∠BCD=180°-∠ABC=90°,
∠ADC=∠ABC=90°,
∴∠BAD=∠BCD=90°(平行四边形的对角相等).
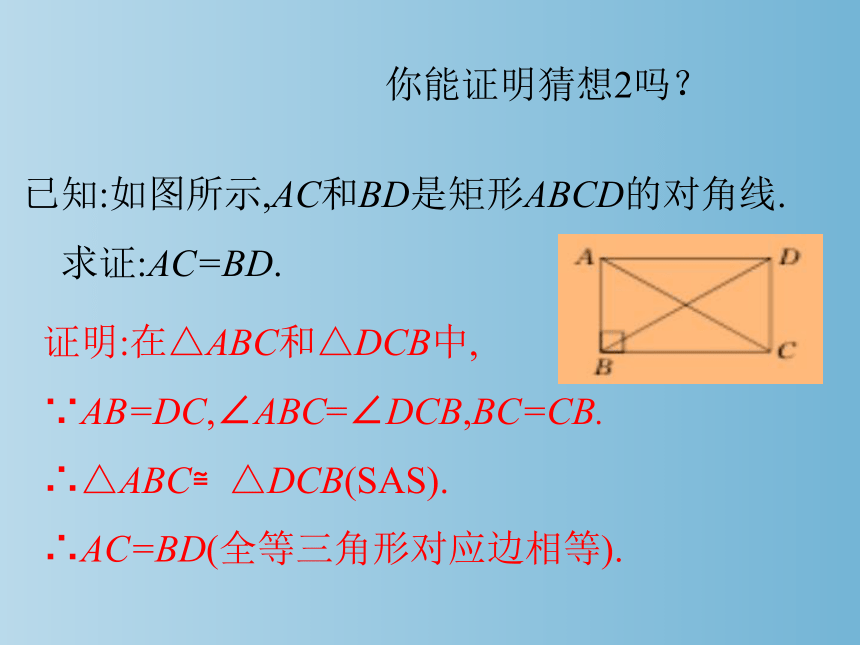
你能证明猜想2吗?
已知:如图所示,AC和BD是矩形ABCD的对角线.
求证:AC=BD.
证明:在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC=CB.
∴△ABC≌△DCB(SAS).
∴AC=BD(全等三角形对应边相等).
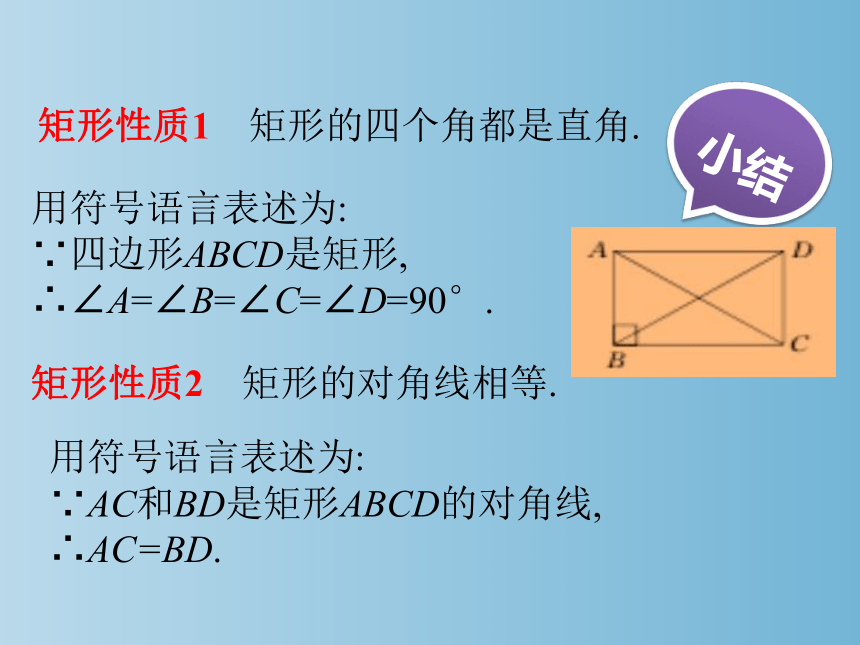
矩形性质1 矩形的四个角都是直角.
用符号语言表述为:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
小结
矩形性质2 矩形的对角线相等.
用符号语言表述为:
∵AC和BD是矩形ABCD的对角线,
∴AC=BD.
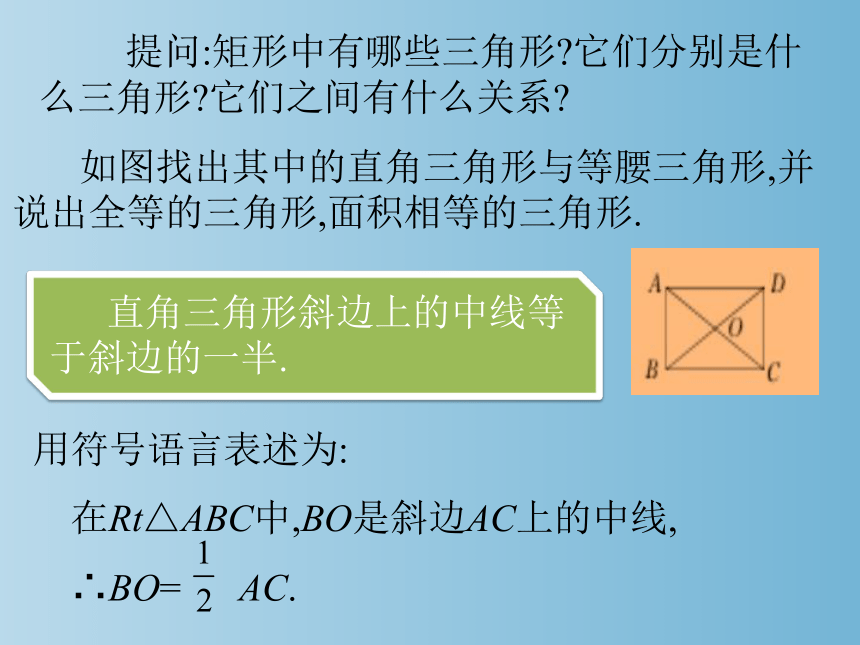
提问:矩形中有哪些三角形 它们分别是什么三角形 它们之间有什么关系
如图找出其中的直角三角形与等腰三角形,并说出全等的三角形,面积相等的三角形.
直角三角形斜边上的中线等于斜边的一半.
用符号语言表述为:
在Rt△ABC中,BO是斜边AC上的中线,
∴BO= AC.
如图,在直角三角形草地上修两条互相交叉的小路BO,EF,路口端点处E,F,O分别为三角形草地的三边中点,小路BO,EF的长度相等吗 请说明理由.
(1)直角三角形中,斜边上的中线把直角三角形
分成两个等腰三角形,这两个等腰三角形的
面积相等.
知识拓展
(2)在直角三角形中,如果遇到斜边的中点,可以
考虑利用这一性质.
(3)直角三角形斜边上的中线的性质一般可以
用来证明线段相等或线段的倍分问题.
例:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求矩形对角线的长.
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分,
∴OA=OB.
又∠AOB=60°,
∴△AOB是等边三角形.
∴OA=AB=4.
∴AC=BD=2OA=8.
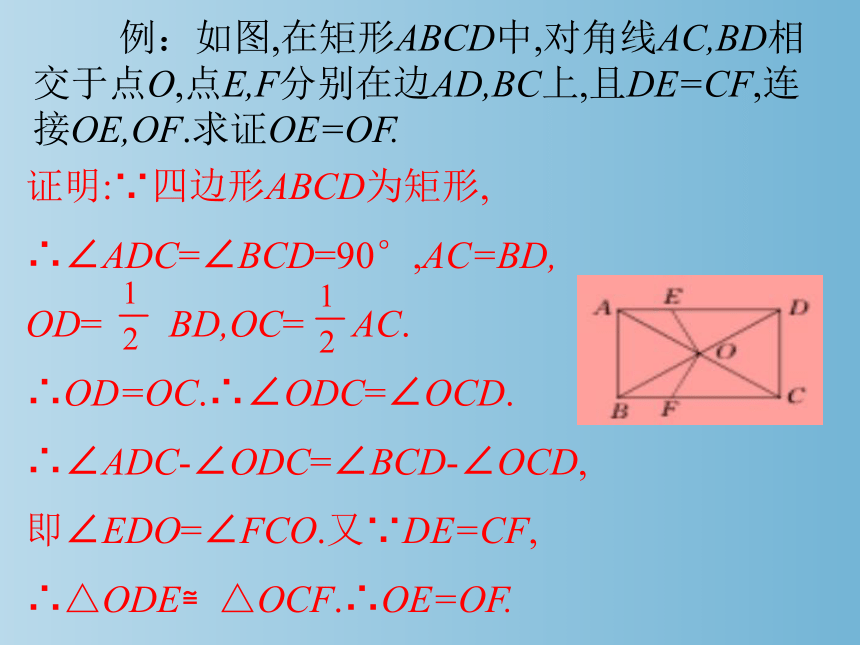
例:如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证OE=OF.
证明:∵四边形ABCD为矩形,
∴∠ADC=∠BCD=90°,AC=BD,
OD= BD,OC= AC.
∴OD=OC.∴∠ODC=∠OCD.
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠EDO=∠FCO.又∵DE=CF,
∴△ODE≌△OCF.∴OE=OF.
小结
图形 定义 性质 边 角 对角线
平行四边形 有两组对边分别平行的四边形叫做平行四边形 对边平行且相等 对角相等、邻角互补 对角线互相平分
矩形 有一个角是直角的平行四边形叫做矩形 对边平行且相等 四个角都是直角 对角线相等且互相平分
1.用矩形纸片折出直角的平分线,下图中的折法正确的是 ( )
D
2.如图,一个矩形纸片,剪去部分后得到一个三
角形,则图中∠1+∠2的度数是 ( )
A.30° B.60° C.90° D.120°
C
3.如图,把矩形纸片沿对角线BD折叠,重叠部分为△EBD,则下列
说法错误的是 ( )
A..AB=CD B.∠BAE=∠DCE C.EB=ED D.∠ABE一定等于30°
D
4.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
20
5.矩形ABCD的周长为40 cm,O是它的对角线交点,若△AOB的周长比△AOD的周长多4 cm,则矩形ABCD的最长边的长为 .
12 cm
6.如图,已知矩形ABCD,点E为矩形外一点,且AE=DE.求证BE=CE.
证明:∵AE=DE,∴∠EAD=∠EDA,
由四边形ABCD是矩形得AB=CD,∠BAD=∠CDA=90°,
∴∠EAD+∠BAD=∠EDA+∠CDA,即∠BAE=∠CDE,在△ABE和△DCE中,
∴△ABE≌△DCE,∴BE=CE.
八年级数学·下 新课标[人]
第十八章 平行四边形
18.2.1 矩 形(第2课时)
工人师傅为了检验两组对边相等的四边形窗框是否为矩形,常常要量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗
(1)命题“矩形的对角线相等”的条件
是 结论是 .
它的逆命题是 ,该逆命题是 命题(填“真”或“假”).
四边形是矩形
对角线相等
对角线相等的四边形是矩形
真
(2)命题“矩形的四个角都是直角”的条件是
;结论是 .
它的逆命题是 .
该逆命题是 命题(填“真”或“假”).
四边形是矩形
四个角都是直角
四个角都是直角的四边形是矩形
真
已知:如图,在□ABCD中,对角线AC=BD.
求证:□ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=DC(平行四边形的对边相等).
又∵BC=CB,AC=DB,∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB. 由题意知AB∥DC.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB= ×180°=90°.
∴□ABCD是矩形.
定理:对角线相等的平行四边形是矩形.
∵在□ABCD中,AC=BD,
∴□ABCD是矩形.
小结
已知:如图,四边形ABCD中,∠A=∠B=∠C=∠D=90°.
求证:四边形ABCD是矩形.
证明:∵∠A+∠B=180°,
∴AD∥BC.∵∠B+∠C=180°,
∴AB∥DC.∴四边形ABCD是平行四边形
又∵∠A=90°,
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
有三个角是直角的四边形是矩形吗
定理:有三个角是直角的四边形是矩形.
∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
已知:如图,四边形ABCD中,∠A=∠B=∠C=90°,
求证:四边形ABCD是矩形.
证明:∵∠A+∠B=180°,
∴AD∥BC.
∵∠B+∠C=180°,
∴AB∥DC.
∴四边形ABCD是平行四边形.
又∵∠A=90°,
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
应用矩形的判定定理时需要注意的问题:
知识拓展
(1)注意区别“四边形”与“平行四边形”.如判定定理
“对角线相等的平行四边形是矩形”要求满足的
条件是“对角线相等”和“平行四边形”;判定定理
“三个角都是直角的四边形是矩形”要求满足的
条件是“三个角都是直角”和“四边形”.
(2)无论是定义还是判定定理,运用时一定要分清它的
条件与结论.
例:判断:
(1)两条对角线相等的四边形是矩形. ( )
(2)两条对角线相等且互相平分的四边形是矩形. ( )
(3)有一个角是直角的四边形是矩形. ( )
√
例:如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°,求∠OAB的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,OB=OD= BD.
又OA=OD,∴AC=BD.
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形),
∴∠DAB=90°(矩形的四个角都是直角),
又∠OAD=50°,∴∠OAB=40°.
小结
矩形的判定方法分两类:从四边形来判定和从平行四边形来判定.常用的判定方法有三种:
① 矩形的定义:有一个角是直角的平行四边形是矩形;
②矩形的判定定理:对角线相等的平行四边形是矩形;
③矩形的判定定理:三个角都是直角的四边形是矩形.
1.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是 ( )
A.AB=BE B.DE⊥DC C.∠ADB=90° D.CE⊥DE
B
2.工人师傅在做门框或矩形零件时,常用测量平行四边形两条对角线是否相等来检测直角的精度,工人师傅依据的几何道理
是 .
对角线相等的平行四边形是矩形
3.如图,要使平行四边形ABCD成为矩形,应添加的条件是 (只填一个).
∠ABC=90°
4.如图所示,矩形ABCD的对角线AC,BD相交于O,E,F,G,H分别是OA,OB,OC,OD的中点.
求证四边形EFGH是矩形.
证明:∵矩形ABCD的对角线AC,BD相交于O,
∴AO=BO=CO=DO.
又∵E,F,G,H分别是OA,OB,OC,OD的中点,∴EO=FO=GO=HO.
∴四边形EFGH为平行四边形,EG=HF,
∴四边形EFGH是矩形.
谢 谢 观 看
八年级数学·下 新课标[人]
第十八章 平行四边形
18.2.1 矩 形(第1课时)
一个活动的平行四边形教具,轻轻拉动一个点,不管怎么拉,它还是一个平行四边形吗 为什么
有一个角是直角的平行四边形叫做矩形,也就是长方形.
提问:如图,矩形A'B'C'D'的边、角、对角线方面是否有不同于一般平行四边形的特殊性质 你能得出有关性质的猜想吗
猜想1:矩形的四个角都是直角;
猜想2:矩形的对角线相等.
追问:你能证明这些猜想吗
你能证明猜想1吗?
在矩形ABCD中,AB∥CD,
∴∠BCD=180°-∠ABC=90°,
∠ADC=∠ABC=90°,
∴∠BAD=∠BCD=90°(平行四边形的对角相等).
你能证明猜想2吗?
已知:如图所示,AC和BD是矩形ABCD的对角线.
求证:AC=BD.
证明:在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC=CB.
∴△ABC≌△DCB(SAS).
∴AC=BD(全等三角形对应边相等).
矩形性质1 矩形的四个角都是直角.
用符号语言表述为:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
小结
矩形性质2 矩形的对角线相等.
用符号语言表述为:
∵AC和BD是矩形ABCD的对角线,
∴AC=BD.
提问:矩形中有哪些三角形 它们分别是什么三角形 它们之间有什么关系
如图找出其中的直角三角形与等腰三角形,并说出全等的三角形,面积相等的三角形.
直角三角形斜边上的中线等于斜边的一半.
用符号语言表述为:
在Rt△ABC中,BO是斜边AC上的中线,
∴BO= AC.
如图,在直角三角形草地上修两条互相交叉的小路BO,EF,路口端点处E,F,O分别为三角形草地的三边中点,小路BO,EF的长度相等吗 请说明理由.
(1)直角三角形中,斜边上的中线把直角三角形
分成两个等腰三角形,这两个等腰三角形的
面积相等.
知识拓展
(2)在直角三角形中,如果遇到斜边的中点,可以
考虑利用这一性质.
(3)直角三角形斜边上的中线的性质一般可以
用来证明线段相等或线段的倍分问题.
例:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求矩形对角线的长.
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分,
∴OA=OB.
又∠AOB=60°,
∴△AOB是等边三角形.
∴OA=AB=4.
∴AC=BD=2OA=8.
例:如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证OE=OF.
证明:∵四边形ABCD为矩形,
∴∠ADC=∠BCD=90°,AC=BD,
OD= BD,OC= AC.
∴OD=OC.∴∠ODC=∠OCD.
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠EDO=∠FCO.又∵DE=CF,
∴△ODE≌△OCF.∴OE=OF.
小结
图形 定义 性质 边 角 对角线
平行四边形 有两组对边分别平行的四边形叫做平行四边形 对边平行且相等 对角相等、邻角互补 对角线互相平分
矩形 有一个角是直角的平行四边形叫做矩形 对边平行且相等 四个角都是直角 对角线相等且互相平分
1.用矩形纸片折出直角的平分线,下图中的折法正确的是 ( )
D
2.如图,一个矩形纸片,剪去部分后得到一个三
角形,则图中∠1+∠2的度数是 ( )
A.30° B.60° C.90° D.120°
C
3.如图,把矩形纸片沿对角线BD折叠,重叠部分为△EBD,则下列
说法错误的是 ( )
A..AB=CD B.∠BAE=∠DCE C.EB=ED D.∠ABE一定等于30°
D
4.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
20
5.矩形ABCD的周长为40 cm,O是它的对角线交点,若△AOB的周长比△AOD的周长多4 cm,则矩形ABCD的最长边的长为 .
12 cm
6.如图,已知矩形ABCD,点E为矩形外一点,且AE=DE.求证BE=CE.
证明:∵AE=DE,∴∠EAD=∠EDA,
由四边形ABCD是矩形得AB=CD,∠BAD=∠CDA=90°,
∴∠EAD+∠BAD=∠EDA+∠CDA,即∠BAE=∠CDE,在△ABE和△DCE中,
∴△ABE≌△DCE,∴BE=CE.
八年级数学·下 新课标[人]
第十八章 平行四边形
18.2.1 矩 形(第2课时)
工人师傅为了检验两组对边相等的四边形窗框是否为矩形,常常要量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗
(1)命题“矩形的对角线相等”的条件
是 结论是 .
它的逆命题是 ,该逆命题是 命题(填“真”或“假”).
四边形是矩形
对角线相等
对角线相等的四边形是矩形
真
(2)命题“矩形的四个角都是直角”的条件是
;结论是 .
它的逆命题是 .
该逆命题是 命题(填“真”或“假”).
四边形是矩形
四个角都是直角
四个角都是直角的四边形是矩形
真
已知:如图,在□ABCD中,对角线AC=BD.
求证:□ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=DC(平行四边形的对边相等).
又∵BC=CB,AC=DB,∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB. 由题意知AB∥DC.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB= ×180°=90°.
∴□ABCD是矩形.
定理:对角线相等的平行四边形是矩形.
∵在□ABCD中,AC=BD,
∴□ABCD是矩形.
小结
已知:如图,四边形ABCD中,∠A=∠B=∠C=∠D=90°.
求证:四边形ABCD是矩形.
证明:∵∠A+∠B=180°,
∴AD∥BC.∵∠B+∠C=180°,
∴AB∥DC.∴四边形ABCD是平行四边形
又∵∠A=90°,
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
有三个角是直角的四边形是矩形吗
定理:有三个角是直角的四边形是矩形.
∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
已知:如图,四边形ABCD中,∠A=∠B=∠C=90°,
求证:四边形ABCD是矩形.
证明:∵∠A+∠B=180°,
∴AD∥BC.
∵∠B+∠C=180°,
∴AB∥DC.
∴四边形ABCD是平行四边形.
又∵∠A=90°,
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
应用矩形的判定定理时需要注意的问题:
知识拓展
(1)注意区别“四边形”与“平行四边形”.如判定定理
“对角线相等的平行四边形是矩形”要求满足的
条件是“对角线相等”和“平行四边形”;判定定理
“三个角都是直角的四边形是矩形”要求满足的
条件是“三个角都是直角”和“四边形”.
(2)无论是定义还是判定定理,运用时一定要分清它的
条件与结论.
例:判断:
(1)两条对角线相等的四边形是矩形. ( )
(2)两条对角线相等且互相平分的四边形是矩形. ( )
(3)有一个角是直角的四边形是矩形. ( )
√
例:如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°,求∠OAB的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,OB=OD= BD.
又OA=OD,∴AC=BD.
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形),
∴∠DAB=90°(矩形的四个角都是直角),
又∠OAD=50°,∴∠OAB=40°.
小结
矩形的判定方法分两类:从四边形来判定和从平行四边形来判定.常用的判定方法有三种:
① 矩形的定义:有一个角是直角的平行四边形是矩形;
②矩形的判定定理:对角线相等的平行四边形是矩形;
③矩形的判定定理:三个角都是直角的四边形是矩形.
1.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是 ( )
A.AB=BE B.DE⊥DC C.∠ADB=90° D.CE⊥DE
B
2.工人师傅在做门框或矩形零件时,常用测量平行四边形两条对角线是否相等来检测直角的精度,工人师傅依据的几何道理
是 .
对角线相等的平行四边形是矩形
3.如图,要使平行四边形ABCD成为矩形,应添加的条件是 (只填一个).
∠ABC=90°
4.如图所示,矩形ABCD的对角线AC,BD相交于O,E,F,G,H分别是OA,OB,OC,OD的中点.
求证四边形EFGH是矩形.
证明:∵矩形ABCD的对角线AC,BD相交于O,
∴AO=BO=CO=DO.
又∵E,F,G,H分别是OA,OB,OC,OD的中点,∴EO=FO=GO=HO.
∴四边形EFGH为平行四边形,EG=HF,
∴四边形EFGH是矩形.
谢 谢 观 看
