12..5因式分解 第2课时 完全平方公式 课件(共22张PPT) 华东师大版数学八年级上册
文档属性
| 名称 | 12..5因式分解 第2课时 完全平方公式 课件(共22张PPT) 华东师大版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
12.5因式分解
公式法
第2课时
完全平方公式
复习引入
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
(1)提公因式法
(2)平方差公式a2-b2=(a+b(a-b)
填一填:在横线上填上适当的式子,使等式成立
(1)(a+b)2=2+2ah+b
a2+2a+1=(a+1)
(a-b)'=d2-2ab+b
a2-_2a
+1=(a-1)1
(2)根据(1)填空:
a'+2ab+b2 (a+b)'
a2-2ab+b3=(a-b)2
我们把2+2ab+b2和a2-2ab+b2这样的式子叫做
完全平方式
观察这两个式子:
a2+2ab b2
a2-2ab+b
(1)每个多项式有几项?三项
(2)每个多项式的第一项和第三项有什么特征?
这两项都是数或式的平方,并且符号相同
(3)中间项和第一项,第三项有什么关系?
是第一项和第三项底数的积的士2倍
完全平方式:a2±2ab+b2
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个数或式的平方和;
3.有两底数之积的±2倍.
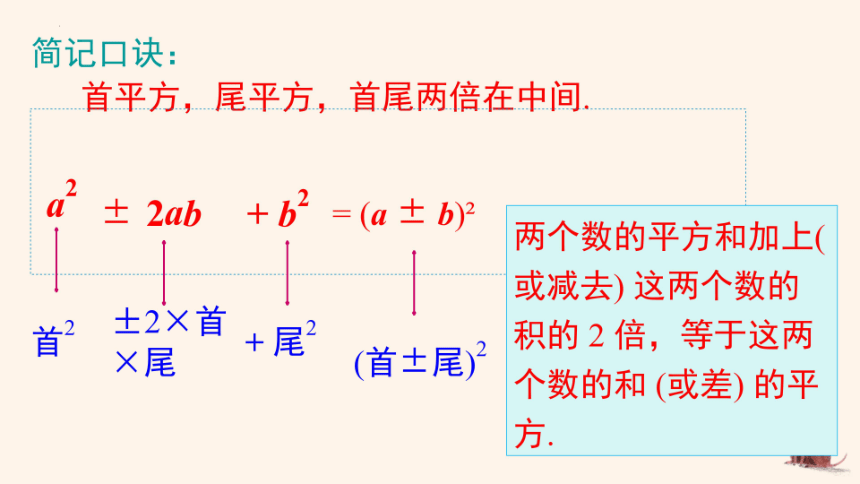
简记口诀:
首平方,尾平方,首尾两倍在中间
±2ab
+b2=(a±b)2
两个数的平方和加上(
.
或减去)这两个数的
首2
士2X首
+尾
积的2倍,等于这两
×尾
(首±尾)2
个数的和(或差)的平
方.
对照a2±2ab+b2=(a±b)2,填空:
1.x2+4x+4=(x)2+2(x)(2)+(2)2=(x+2)2
2.m2-6m+9=(m)2-2.(m)(3)+(3)2=(m-3)2
3.a2+4ab+4b2=(a)2+2(a)·(2b)+(2b)2=(a+2b)2
下列各式是不是完全平方式?
(1)a2-4a+4;是
(2)1+4a2;不是
(3)4b2+4b-1;不是
(4)a2+ab+b2;不是
(5)x2+x+0.25.是
分析:(2)因为它只有两项;
(3)4b2与-1的符号不统一;
(4)因为b不是a与b的积的2倍.
类型1:完全平方式求值
例1如果x2-6x+N是一个完全平方式,那么N=(B)
A.11
B.9
C.-11
D.-9
解析:根据完全平方式的特征,中间项-6x=2x×(-3),
故可知N=(-3)2=9.
变式训练如果x2-mx+16是一个完全平方式,那么m
的值为
±8
类型2:完全平方式因式分解
例2分解因式:
(1)x2+10x+25;
(2)-x2+4xy-42.
分析:(1)中x2=x2,25=5;
10x=2X5x;
x2+10x+25=
x2+2X5x+(3)2.
2
+2ab
+b2
12.5因式分解
公式法
第2课时
完全平方公式
复习引入
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
(1)提公因式法
(2)平方差公式a2-b2=(a+b(a-b)
填一填:在横线上填上适当的式子,使等式成立
(1)(a+b)2=2+2ah+b
a2+2a+1=(a+1)
(a-b)'=d2-2ab+b
a2-_2a
+1=(a-1)1
(2)根据(1)填空:
a'+2ab+b2 (a+b)'
a2-2ab+b3=(a-b)2
我们把2+2ab+b2和a2-2ab+b2这样的式子叫做
完全平方式
观察这两个式子:
a2+2ab b2
a2-2ab+b
(1)每个多项式有几项?三项
(2)每个多项式的第一项和第三项有什么特征?
这两项都是数或式的平方,并且符号相同
(3)中间项和第一项,第三项有什么关系?
是第一项和第三项底数的积的士2倍
完全平方式:a2±2ab+b2
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个数或式的平方和;
3.有两底数之积的±2倍.
简记口诀:
首平方,尾平方,首尾两倍在中间
±2ab
+b2=(a±b)2
两个数的平方和加上(
.
或减去)这两个数的
首2
士2X首
+尾
积的2倍,等于这两
×尾
(首±尾)2
个数的和(或差)的平
方.
对照a2±2ab+b2=(a±b)2,填空:
1.x2+4x+4=(x)2+2(x)(2)+(2)2=(x+2)2
2.m2-6m+9=(m)2-2.(m)(3)+(3)2=(m-3)2
3.a2+4ab+4b2=(a)2+2(a)·(2b)+(2b)2=(a+2b)2
下列各式是不是完全平方式?
(1)a2-4a+4;是
(2)1+4a2;不是
(3)4b2+4b-1;不是
(4)a2+ab+b2;不是
(5)x2+x+0.25.是
分析:(2)因为它只有两项;
(3)4b2与-1的符号不统一;
(4)因为b不是a与b的积的2倍.
类型1:完全平方式求值
例1如果x2-6x+N是一个完全平方式,那么N=(B)
A.11
B.9
C.-11
D.-9
解析:根据完全平方式的特征,中间项-6x=2x×(-3),
故可知N=(-3)2=9.
变式训练如果x2-mx+16是一个完全平方式,那么m
的值为
±8
类型2:完全平方式因式分解
例2分解因式:
(1)x2+10x+25;
(2)-x2+4xy-42.
分析:(1)中x2=x2,25=5;
10x=2X5x;
x2+10x+25=
x2+2X5x+(3)2.
2
+2ab
+b2
