苏科版2023-2024学年度上学期九年级期末必考数学练习卷(含解析)
文档属性
| 名称 | 苏科版2023-2024学年度上学期九年级期末必考数学练习卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 16:16:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末必考题练习卷-2023-2024学年九年级上册苏科版
一、单选题
1.“敬老爱老”是中华民族的优秀传统美德.小刚、小强计划利用暑期从,,三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )
A. B. C. D.
2.已知,的半径为一元二次方程的两根,圆心到直线的距离,则直线与的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
3.下列方程一定是关于x的一元二次方程的是( )
A. B. C. D.
4.已知圆内接四边形中,,则的度数为( )
A. B. C. D.
5.方程是关于的一元二次方程,则的取值范围是( )
A. B. C. D.
6.甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次 第二次 第三次 第四次
甲 87 95 85 93
乙 80 80 90 90
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为,,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定
7.某农场2019年的产值为80万元,通过改进技术,2021年的产值达到96.8万元,求该农场这两年产值的年平均增长率.设该农场这两年产值的年平均增长率为x,根据题意可列方程为( )
A. B.
C. D.
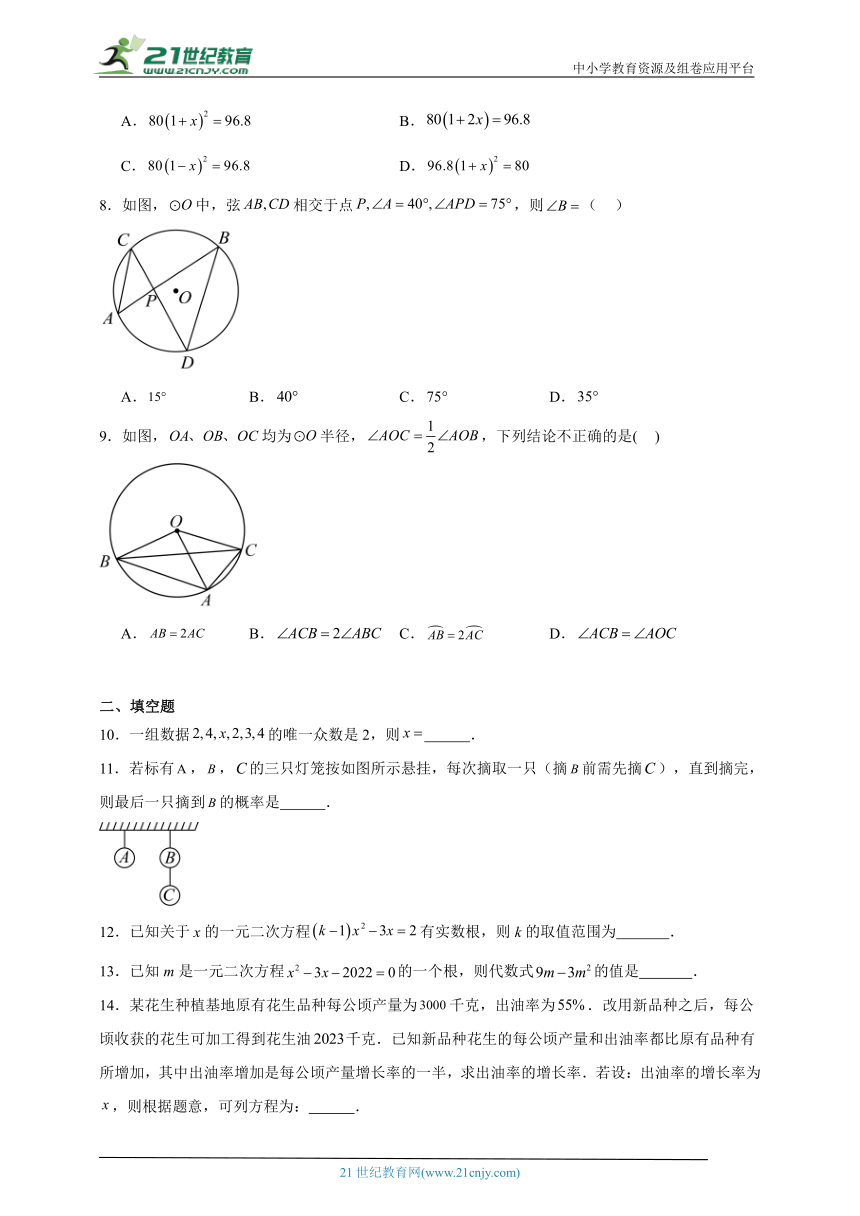
8.如图,中,弦相交于点,则( )
A. B. C. D.
9.如图,均为半径,,下列结论不正确的是( )
A. B. C. D.
二、填空题
10.一组数据的唯一众数是2,则 .
11.若标有,,的三只灯笼按如图所示悬挂,每次摘取一只(摘前需先摘),直到摘完,则最后一只摘到的概率是 .
12.已知关于x的一元二次方程有实数根,则k的取值范围为 .
13.已知m是一元二次方程的一个根,则代数式的值是 .
14.某花生种植基地原有花生品种每公顷产量为千克,出油率为.改用新品种之后,每公顷收获的花生可加工得到花生油千克.已知新品种花生的每公顷产量和出油率都比原有品种有所增加,其中出油率增加是每公顷产量增长率的一半,求出油率的增长率.若设:出油率的增长率为,则根据题意,可列方程为: .
15.如图,直径,,则 .
16.如图,已知半圆的直径,沿弦翻折,翻折后的与直径相切于点D,且,则折痕的长度是 ;
17.筒车是我国古代发明的一种水利灌溉工具,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图1.唐代陈廷章在《水轮赋》中写道“水能利物,轮乃曲成”.如图2,已知圆心O在水面上方,且被水面截得弦长为8米,若点C为运行轨道的最低点,点C到弦所在直线的距离是2,则的半径长为 米.
三、解答题
18.某体育馆有A,B两个入口,每个入口有3个通道可同时通行,C,D,E三个出口,其中C、D出口有2个通道,E出口只有一个通道,每个通道在规定时间内可通行100人,规定:观众进馆时须持票任意从两个入口进入,出馆时只可任意从三个出口离开.甲、乙、丙三名观众分别从两个入口中随机选择一个入口进入.
(1)求甲从A口进入,C口离开的概率;
(2)求甲、乙、丙三名观众选择同一入口进馆的概率.
(3)学校有七、八、九三个年级的学生进场观看比赛,七年级80人,八年级150人,九年级160人,比赛结束后,为了能够在规定时间内使所有同学都能有序离开,请你合理安排七、八、九三个年级的学生从C、D、E三个出口(每个年级的学生走同一个出口)离开(安排一种即可),并说明理由.
19.设一元二次方程的两个根为,若该方程的一个根与另一个根的2倍的和为0,我们就称这个一元二次方程为“两根相反倍数”方程.
(1)如果方程是“两根相反倍数”方程,则m=______;
(2)如果方程是“两根相反倍数”方程,求的值.
20.平安路上,多“盔”有你,在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶40元,售价为每顶68元,平均每周可售出100顶.商店计划将头盔降价销售,每顶售价不高于58元,经调查发现:每降价2元,平均每周可多售出40顶.设每顶头盔降价x元,平均每周的销售量为y顶.
(1)每顶头盔降价x元后,每顶头盔的利润是 元(用含x的代数式表示);
(2)平均每周的销售量y(顶)与降价x(元)之间的函数关系式是 ;
(3)若该商店希望平均每周获得4000元的销售利润,则每顶头盔应降价多少?
21.如图,在中,直径,垂足为M,若,.
(1)证明:;
(2)求的半径.
22.如图,是被直径分成的半圆上一点,过点的的切线交的延长线于点,连接,,.
(1)求证:;
(2)若,,求图中阴影部分的面积(结果保留和根号).
23.如图,内接于,为的直径,点为上的一动点,且在上方(点不与点A,重合),.
(1)试判断的形状,并说明理由;
(2)连接,求证:;
(3)若关于直线的对称图形为,连接,试探究,,三者之间的等量关系,并证明你的结论.
24..某校为了普及环保知识,从七、八两个年级中各选出10名学生参加环保知识竞赛(满分100分),并对成绩进行整理分析,得到如下信息:
平均数 众数 中位数
七年级参赛学生成绩 85.5 m 87
八年级参赛学生成绩 85.5 85 n
根据以上信息,回答下列问题:
(1)填空:________,________;
(2)七、八年级参赛学生成绩的方差分别记为、,请判断___________(填“”“”或“”);
(3)从平均数和中位数的角度分析哪个年级参赛学生的成绩较好.
参考答案:
1.B
【分析】画出树状图展示所有9种等可能的结果数,找出两人恰好选择同一场所的结果数,然后根据概率公式求解.
【详解】解:画树状图如图:
共有9种等可能的结果数,其中两人恰好选择同一场所的结果数为3,
∴明明和亮亮两人恰好选择同一场馆的概率,
故选:B.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
2.A
【分析】本题考查了因式分解来解一元二次方程以及直线与圆的位置关系:当,直线与圆相交,当,直线与圆相切,当,直线与圆相离,据此即可作答.
【详解】解:∵
∴
故的半径为,
∵
∴
即直线与圆相交
故选:A
3.C
【分析】本题考查了一元二次方程的定义“只含有1个未知数,并且未知数的最高次数为2的整式方程即为一元二次方程”.根据一元二次方程的定义逐项判断即可得.
【详解】解:A、方程不是整式方程,则此项不符合题意;
B、方程整理为,是一元一次方程,则此项不符合题意;
C、方程整理为,是一元二次方程,则此项符合题意;
D、方程中当时,方程为,是一元一次方程,则此项不符合题意;
故选:C.
4.D
【分析】本题考查了圆内接四边形对角互补,先设,列式算出的值,再的值,根据圆内接四边形对角互补,列式计算,即可作答.
【详解】解:∵,
∴设,
则,
即,
所以,
那么,
故选:D.
5.A
【分析】本题主要考查一元二次方程的概念,满足二次项系数不为,并且二次项的次数是,直接计算即可求解的值.
【详解】解:∵是一元二次方程;
∴;
∴;
∵;
∴;
故选:A.
6.B
【分析】根据众数、中位数、平均数的求解方法以及方差的意义逐项计算、判断即可作答.
【详解】A项,甲同学四次数学测试成绩的平均数是分,故原说法错误,本项不符合题意;
B项,甲同学四次数学测试成绩的中位数是分,故说法正确,本项符合题意;
C项,乙同学四次数学测试成绩的众数是80分和90分,故原说法错误,本项不符合题意;
D项,根据方差越小数据越稳定,可知甲同学四次数学测试成绩较稳定,故原说法错误,本项不符合题意;
故选:B.
【点睛】本题主要考查了众数、中位数、平均数的求解方法以及方差的意义,掌握方差越小数据越稳定,是解答本题的关键.
7.A
【分析】本题考查了由实际问题抽象出一元二次方程的运用,增长率问题,一般用增长后的量=增长前的量×(1+增长率),参照本题,如果年平均增长率为x,根据“2019年产值80万元,2021年产值96.8万元”即可得出方程.
【详解】解:根据题意得:2019的产值为:80万元,则:2021的产值为:万元.
那么可得方程:.
故选:A.
8.D
【分析】本题主要考查圆周角定理及三角形外角的性质,熟练掌握相关知识点是解题的关键.根据圆周角定理可知,即可利用外角性质求出.
【详解】解:∵,
∴,
又∵,,
∴,
故选:D.
9.A
【分析】本题考查了弧、弦与圆心角的关系以及圆周角定理,首先取的中点,连接,,由,易得,继而证得;又由圆周角定理,可得,.
【详解】解:取的中点,连接,,
,
,
,
,
,
.
故A错误,符合题意,故C正确,不符合题意;
,,
,
,
,
故B、D正确,不符合题意;
故选:A.
10.2
【解析】略
11.
【分析】本题主要考查了树状图法或列表法求解概率,先画出树状图得到所有等可能性的结果数,再找到最后一只摘到的结果数,最后根据概率计算公式求解即可.
【详解】解:画树状图如图:
由树状图可知,共有个等可能的结果,最后一只摘到的结果有个,
最后一只摘到的概率为,
故答案为:.
12.且
【分析】此题考查了一元二次方程根的判别式,以及一元二次方程的定义,根据方程有实数根可以得到根的判别式大于等于0,再根据一元二次方程的定义得到,由此求出k的范围即可;
【详解】解:∵方程有实数根,
,且,
解得:且;
故答案为:且.
13.
【分析】本题考查一元二次方程的解的定义,代数式求值.将代入一元二次方程即可得出,再将代数式变形为,最后整体代入即可.
【详解】解:∵m为一元二次方程的一个根,
∴,
∴,
∴.
故答案为:.
14.
【分析】本题考查了一元二次方程的应用——增长率问题,找到等量关系准确地列出方程是解决问题的关键.根据“出油率增加是每公顷产量增长率的一半”可得公顷产量增长率为,根据“原有花生品种每公顷产量为千克,出油率为.改用新品种之后,每公顷收获的花生可加工得到花生油千克”即可列出关于的一元二次方程.
【详解】解:出油率增长率为,则公顷产量增长率为,依题意有:
,
故答案为:.
15.
【分析】本题考查了圆周角定理.连接,由,得到是等边三角形,据此求解即可.
【详解】解:连接,如图,
∵,
∴,
∵,
∴是等边三角形,
∴,
又∵直径,
∴,
∴.
故答案为:.
16.
【分析】根据折叠的性质可得折叠后的圆与圆半径一样,设折叠后的圆弧所对的圆心为,根据相交圆的性质可以得到与互相垂直平分,由勾股定理就可以求出和的值,从而求得结果.
【详解】解:设折叠后的圆弧所对的圆心为,连接,,,与交于点M,如图所示:
,
∴与互相垂直平分,
∴,,
∵,
∴,
以点为圆心的圆半径也是2,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
即折痕的长为,
故答案为:.
【点睛】本题考查了翻折的性质的运用,相交圆的性质的应用,勾股定理的运用,垂直平分线性质的运用,根据相交圆的性质求解是解题的关键.
17.5
【分析】本题考查垂径定理的应用,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.连接交于点E.利用垂径定理得,再利用勾股定理即可求出半径.
【详解】解:连接交于点E.设,
由题意,
∴(米),
∵,
∴,
在中,,
∴米,
故答案为:5.
18.(1)
(2)
(3)七年级走E出口,八九年级走C、D出口,理由见解析
【分析】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.(1)画树状图,共有6种等可能的结果,其中甲从A口进入,C口离开的结果有1种,再由概率公式求解即可;(2)画树状图,共有8种等可能的结果,其中甲、乙、丙三名观众选择同一入口进馆的结果有2种,再由概率公式求解即可;(3)满足题意的方案即可.
【详解】(1)解:(1)画树状图如下:共有6种等可能的结果,其中甲从A口进入,C口离开的结果有1种,
∴甲从A口进入,C口离开的概率为;
(2)画树状图如下:共有8种等可能的结果,其中甲、乙、丙三名观众选择同一入口进馆的结果有2种,
∴甲、乙、丙三名观众选择同一入口进馆的概率为.
(3)七年级走E出口,八九年级走C、D出口.
理由:因为七年级80人,八年级150人,九年级160人,又因为C、D出口有2个通道,E出口只有一个通道,且每个通道在规定时间内可通行100人,所以按七年级走E出口,八九年级走C、D出口方案,能够在规定时间内使所有同学都能有序离开.
19.(1)
(2)或.
【分析】本题考查了一元二次方程根与系数的关系;
(1)根据新定义可得,根据根与系数的关系得:, 得出,,进而代入,即可求解;
(2)分两种情况:设,则,或,则;根据(1)的方法,分别求得的值,代入代数式,即可求解.
【详解】(1)解:∵方程是“两根相反倍数”方程,
∴,
根据根与系数的关系得:,
∴,
∴
解得:
当,
∴,
∴
解得:
(2)分两种情况:设,则
根据根与系数的关系得:,
解得:,
设,则
根据根与系数的关系得:
,
解得:,
20.(1)
(2)
(3)每顶头盔应降价20元
【分析】本题主要考查了一元二次方程的应用以及一次函数的应用,解题的关键是:根据各数量之间的关系,找出y关于x的函数关系式;根据各数量之间的关系,列式计算;找准等量关系,正确列出一元二次方程.
(1)根据利润售价进价,列出代数式即可;
(2)利用平均每周的销售量,即可找出与之间的函数关系式;
(3)利用每周的销售利润每顶的销售利润每周的销售量,可列出关于的一元二次方程,解之可求出的值,再结合降价后每顶头盔的售价不高于元,即可确定结论.
【详解】(1)解:∵进价为每顶40元,原售价为每顶68元,
∴每顶头盔降价x元后,每顶头盔的利润是元;
故答案为:;
(2)解:根据题意得:,
故答案为:;
(3)解:根据题意得:,
解得:,,
当时,,不符合题意,舍去;
当时,,符合题意.
答:每顶头盔应降价20元.
21.(1)过程见解析
(2)5
【分析】(1)先根据垂径定理得,,再根据圆周角定理得出答案;
(2)设半径是r,可知,,根据垂径定理得,再根据勾股定理列出方程,求出解即可.
【详解】(1)连接.
∵,
∴,
∴.
∵,
∴,
即;
(2)设半径是r,则,.
∵,,
∴.
在中,,
即,
解得.
所以的半径是5.
【点睛】本题主要考查了垂径定理,圆周角定理及推论,勾股定理等,勾股定理是求线段长的常用方法.
22.(1)见解析;
(2)图中阴影部分的面积是.
【分析】()由是半圆的直径,是半圆的切线,可得,即得;
()由得,可得,,即得,再利用阴影部分的面积等于半圆减去即可解题.
【详解】(1)证明:∵是半圆的直径,
∴,
∵是半圆的切线,
∴,
∴,
∴;
(2)解:由()知,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,,
∴,
∴阴影部分的面积是,
答:阴影部分的面积是.
【点睛】此题考查了圆的切线性质,含角的直角三角形的性质,圆周角定理,求扇形面积,综合运用以上知识是解题的关键.
23.(1)为等腰直角三角形
(2)证明见解析
(3),证明见解
【分析】(1)由直径所对的圆周角为可得:,再根据圆周角定理可得,再结合可得,由等角对等边可得即可解答;
(2)如图:作交的延长线于点D,因为,所以,则,所以,再证明可得,所以,则
即可;
(3)如图:延长交于点,连接,由轴对称的性质得,则,所以,,则,再根据圆周角定理可得、,最后根据勾股定理即可解答.
【详解】(1)解:,
∴
又,
,
又是该外接圆的直径
,
为等腰直角三角形
(2)解:如图:作,并延长交于点,
,
为等腰直角三角形,
,
由勾股定理可知,
,
由(1)可知为等腰直角三角形,
,
又,
,
在和中,
,
,
,
(3)解:,证明如下:
如图,延长交于点,连接,
,
为等腰直角三角形
由勾股定理可求得:,
又,
又,
,即,
为直径,
,
在Rt中,有,
.
【点睛】本题主要考查了圆周角定理、等腰直角三角形的判定与性质、全等三角形的判定与性质、轴对称的性质、勾股定理等知识点,正确地作出所需要的辅助线是解题的关键.
24.(1),
(2)
(3)七年级
【分析】本题考查了平均数,众数,中位数,方差;
(1)利用统计图中的数据可得具体的成绩,再由众数和中位数的定义进行求解即可;
(2)观察统计图,数据波动较大的对应方差较大,即可求解;
(3)由于平均数相同,中位数越大成绩越好,据此即可求解;
理解定义:“由一组数据中出现次数最多的数据是这组数据的众数;一组数据中出现次数最多的数据是这组数据的众数;将这组数据按从小到大的顺序排列,当数据的个数是奇数时,中间的数为中位数,当数据的个数是偶数时,中间两个数的平均数为中位数;一组数据方差越大波动越大,越不稳定;”,并会根据中位数的意义判断决策是解题的关键.
【详解】(1)解:由统计图得
七年级的得分情况为:分名学生,分名学生,分名学生,分名学生,
分名学生,分名学生,分名学生,
个数最多的是,
众数是分,
;
八年级的得分情况按从小到大排列为:,,,,,,,,,,
中间的两个数是,,
中位数分;
故答案:,;
(2)解:观察折线统计图可得
七年级的成绩波动明显比八年级的成绩波动大,
,
故答案:;
(3)解:由题意得
七年级和八年级的平均成绩相同,但是七年级的中位数比八年级的大,所以七年级参赛学生的成绩较好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末必考题练习卷-2023-2024学年九年级上册苏科版
一、单选题
1.“敬老爱老”是中华民族的优秀传统美德.小刚、小强计划利用暑期从,,三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )
A. B. C. D.
2.已知,的半径为一元二次方程的两根,圆心到直线的距离,则直线与的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
3.下列方程一定是关于x的一元二次方程的是( )
A. B. C. D.
4.已知圆内接四边形中,,则的度数为( )
A. B. C. D.
5.方程是关于的一元二次方程,则的取值范围是( )
A. B. C. D.
6.甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次 第二次 第三次 第四次
甲 87 95 85 93
乙 80 80 90 90
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为,,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定
7.某农场2019年的产值为80万元,通过改进技术,2021年的产值达到96.8万元,求该农场这两年产值的年平均增长率.设该农场这两年产值的年平均增长率为x,根据题意可列方程为( )
A. B.
C. D.
8.如图,中,弦相交于点,则( )
A. B. C. D.
9.如图,均为半径,,下列结论不正确的是( )
A. B. C. D.
二、填空题
10.一组数据的唯一众数是2,则 .
11.若标有,,的三只灯笼按如图所示悬挂,每次摘取一只(摘前需先摘),直到摘完,则最后一只摘到的概率是 .
12.已知关于x的一元二次方程有实数根,则k的取值范围为 .
13.已知m是一元二次方程的一个根,则代数式的值是 .
14.某花生种植基地原有花生品种每公顷产量为千克,出油率为.改用新品种之后,每公顷收获的花生可加工得到花生油千克.已知新品种花生的每公顷产量和出油率都比原有品种有所增加,其中出油率增加是每公顷产量增长率的一半,求出油率的增长率.若设:出油率的增长率为,则根据题意,可列方程为: .
15.如图,直径,,则 .
16.如图,已知半圆的直径,沿弦翻折,翻折后的与直径相切于点D,且,则折痕的长度是 ;
17.筒车是我国古代发明的一种水利灌溉工具,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图1.唐代陈廷章在《水轮赋》中写道“水能利物,轮乃曲成”.如图2,已知圆心O在水面上方,且被水面截得弦长为8米,若点C为运行轨道的最低点,点C到弦所在直线的距离是2,则的半径长为 米.
三、解答题
18.某体育馆有A,B两个入口,每个入口有3个通道可同时通行,C,D,E三个出口,其中C、D出口有2个通道,E出口只有一个通道,每个通道在规定时间内可通行100人,规定:观众进馆时须持票任意从两个入口进入,出馆时只可任意从三个出口离开.甲、乙、丙三名观众分别从两个入口中随机选择一个入口进入.
(1)求甲从A口进入,C口离开的概率;
(2)求甲、乙、丙三名观众选择同一入口进馆的概率.
(3)学校有七、八、九三个年级的学生进场观看比赛,七年级80人,八年级150人,九年级160人,比赛结束后,为了能够在规定时间内使所有同学都能有序离开,请你合理安排七、八、九三个年级的学生从C、D、E三个出口(每个年级的学生走同一个出口)离开(安排一种即可),并说明理由.
19.设一元二次方程的两个根为,若该方程的一个根与另一个根的2倍的和为0,我们就称这个一元二次方程为“两根相反倍数”方程.
(1)如果方程是“两根相反倍数”方程,则m=______;
(2)如果方程是“两根相反倍数”方程,求的值.
20.平安路上,多“盔”有你,在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶40元,售价为每顶68元,平均每周可售出100顶.商店计划将头盔降价销售,每顶售价不高于58元,经调查发现:每降价2元,平均每周可多售出40顶.设每顶头盔降价x元,平均每周的销售量为y顶.
(1)每顶头盔降价x元后,每顶头盔的利润是 元(用含x的代数式表示);
(2)平均每周的销售量y(顶)与降价x(元)之间的函数关系式是 ;
(3)若该商店希望平均每周获得4000元的销售利润,则每顶头盔应降价多少?
21.如图,在中,直径,垂足为M,若,.
(1)证明:;
(2)求的半径.
22.如图,是被直径分成的半圆上一点,过点的的切线交的延长线于点,连接,,.
(1)求证:;
(2)若,,求图中阴影部分的面积(结果保留和根号).
23.如图,内接于,为的直径,点为上的一动点,且在上方(点不与点A,重合),.
(1)试判断的形状,并说明理由;
(2)连接,求证:;
(3)若关于直线的对称图形为,连接,试探究,,三者之间的等量关系,并证明你的结论.
24..某校为了普及环保知识,从七、八两个年级中各选出10名学生参加环保知识竞赛(满分100分),并对成绩进行整理分析,得到如下信息:
平均数 众数 中位数
七年级参赛学生成绩 85.5 m 87
八年级参赛学生成绩 85.5 85 n
根据以上信息,回答下列问题:
(1)填空:________,________;
(2)七、八年级参赛学生成绩的方差分别记为、,请判断___________(填“”“”或“”);
(3)从平均数和中位数的角度分析哪个年级参赛学生的成绩较好.
参考答案:
1.B
【分析】画出树状图展示所有9种等可能的结果数,找出两人恰好选择同一场所的结果数,然后根据概率公式求解.
【详解】解:画树状图如图:
共有9种等可能的结果数,其中两人恰好选择同一场所的结果数为3,
∴明明和亮亮两人恰好选择同一场馆的概率,
故选:B.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
2.A
【分析】本题考查了因式分解来解一元二次方程以及直线与圆的位置关系:当,直线与圆相交,当,直线与圆相切,当,直线与圆相离,据此即可作答.
【详解】解:∵
∴
故的半径为,
∵
∴
即直线与圆相交
故选:A
3.C
【分析】本题考查了一元二次方程的定义“只含有1个未知数,并且未知数的最高次数为2的整式方程即为一元二次方程”.根据一元二次方程的定义逐项判断即可得.
【详解】解:A、方程不是整式方程,则此项不符合题意;
B、方程整理为,是一元一次方程,则此项不符合题意;
C、方程整理为,是一元二次方程,则此项符合题意;
D、方程中当时,方程为,是一元一次方程,则此项不符合题意;
故选:C.
4.D
【分析】本题考查了圆内接四边形对角互补,先设,列式算出的值,再的值,根据圆内接四边形对角互补,列式计算,即可作答.
【详解】解:∵,
∴设,
则,
即,
所以,
那么,
故选:D.
5.A
【分析】本题主要考查一元二次方程的概念,满足二次项系数不为,并且二次项的次数是,直接计算即可求解的值.
【详解】解:∵是一元二次方程;
∴;
∴;
∵;
∴;
故选:A.
6.B
【分析】根据众数、中位数、平均数的求解方法以及方差的意义逐项计算、判断即可作答.
【详解】A项,甲同学四次数学测试成绩的平均数是分,故原说法错误,本项不符合题意;
B项,甲同学四次数学测试成绩的中位数是分,故说法正确,本项符合题意;
C项,乙同学四次数学测试成绩的众数是80分和90分,故原说法错误,本项不符合题意;
D项,根据方差越小数据越稳定,可知甲同学四次数学测试成绩较稳定,故原说法错误,本项不符合题意;
故选:B.
【点睛】本题主要考查了众数、中位数、平均数的求解方法以及方差的意义,掌握方差越小数据越稳定,是解答本题的关键.
7.A
【分析】本题考查了由实际问题抽象出一元二次方程的运用,增长率问题,一般用增长后的量=增长前的量×(1+增长率),参照本题,如果年平均增长率为x,根据“2019年产值80万元,2021年产值96.8万元”即可得出方程.
【详解】解:根据题意得:2019的产值为:80万元,则:2021的产值为:万元.
那么可得方程:.
故选:A.
8.D
【分析】本题主要考查圆周角定理及三角形外角的性质,熟练掌握相关知识点是解题的关键.根据圆周角定理可知,即可利用外角性质求出.
【详解】解:∵,
∴,
又∵,,
∴,
故选:D.
9.A
【分析】本题考查了弧、弦与圆心角的关系以及圆周角定理,首先取的中点,连接,,由,易得,继而证得;又由圆周角定理,可得,.
【详解】解:取的中点,连接,,
,
,
,
,
,
.
故A错误,符合题意,故C正确,不符合题意;
,,
,
,
,
故B、D正确,不符合题意;
故选:A.
10.2
【解析】略
11.
【分析】本题主要考查了树状图法或列表法求解概率,先画出树状图得到所有等可能性的结果数,再找到最后一只摘到的结果数,最后根据概率计算公式求解即可.
【详解】解:画树状图如图:
由树状图可知,共有个等可能的结果,最后一只摘到的结果有个,
最后一只摘到的概率为,
故答案为:.
12.且
【分析】此题考查了一元二次方程根的判别式,以及一元二次方程的定义,根据方程有实数根可以得到根的判别式大于等于0,再根据一元二次方程的定义得到,由此求出k的范围即可;
【详解】解:∵方程有实数根,
,且,
解得:且;
故答案为:且.
13.
【分析】本题考查一元二次方程的解的定义,代数式求值.将代入一元二次方程即可得出,再将代数式变形为,最后整体代入即可.
【详解】解:∵m为一元二次方程的一个根,
∴,
∴,
∴.
故答案为:.
14.
【分析】本题考查了一元二次方程的应用——增长率问题,找到等量关系准确地列出方程是解决问题的关键.根据“出油率增加是每公顷产量增长率的一半”可得公顷产量增长率为,根据“原有花生品种每公顷产量为千克,出油率为.改用新品种之后,每公顷收获的花生可加工得到花生油千克”即可列出关于的一元二次方程.
【详解】解:出油率增长率为,则公顷产量增长率为,依题意有:
,
故答案为:.
15.
【分析】本题考查了圆周角定理.连接,由,得到是等边三角形,据此求解即可.
【详解】解:连接,如图,
∵,
∴,
∵,
∴是等边三角形,
∴,
又∵直径,
∴,
∴.
故答案为:.
16.
【分析】根据折叠的性质可得折叠后的圆与圆半径一样,设折叠后的圆弧所对的圆心为,根据相交圆的性质可以得到与互相垂直平分,由勾股定理就可以求出和的值,从而求得结果.
【详解】解:设折叠后的圆弧所对的圆心为,连接,,,与交于点M,如图所示:
,
∴与互相垂直平分,
∴,,
∵,
∴,
以点为圆心的圆半径也是2,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
即折痕的长为,
故答案为:.
【点睛】本题考查了翻折的性质的运用,相交圆的性质的应用,勾股定理的运用,垂直平分线性质的运用,根据相交圆的性质求解是解题的关键.
17.5
【分析】本题考查垂径定理的应用,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.连接交于点E.利用垂径定理得,再利用勾股定理即可求出半径.
【详解】解:连接交于点E.设,
由题意,
∴(米),
∵,
∴,
在中,,
∴米,
故答案为:5.
18.(1)
(2)
(3)七年级走E出口,八九年级走C、D出口,理由见解析
【分析】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.(1)画树状图,共有6种等可能的结果,其中甲从A口进入,C口离开的结果有1种,再由概率公式求解即可;(2)画树状图,共有8种等可能的结果,其中甲、乙、丙三名观众选择同一入口进馆的结果有2种,再由概率公式求解即可;(3)满足题意的方案即可.
【详解】(1)解:(1)画树状图如下:共有6种等可能的结果,其中甲从A口进入,C口离开的结果有1种,
∴甲从A口进入,C口离开的概率为;
(2)画树状图如下:共有8种等可能的结果,其中甲、乙、丙三名观众选择同一入口进馆的结果有2种,
∴甲、乙、丙三名观众选择同一入口进馆的概率为.
(3)七年级走E出口,八九年级走C、D出口.
理由:因为七年级80人,八年级150人,九年级160人,又因为C、D出口有2个通道,E出口只有一个通道,且每个通道在规定时间内可通行100人,所以按七年级走E出口,八九年级走C、D出口方案,能够在规定时间内使所有同学都能有序离开.
19.(1)
(2)或.
【分析】本题考查了一元二次方程根与系数的关系;
(1)根据新定义可得,根据根与系数的关系得:, 得出,,进而代入,即可求解;
(2)分两种情况:设,则,或,则;根据(1)的方法,分别求得的值,代入代数式,即可求解.
【详解】(1)解:∵方程是“两根相反倍数”方程,
∴,
根据根与系数的关系得:,
∴,
∴
解得:
当,
∴,
∴
解得:
(2)分两种情况:设,则
根据根与系数的关系得:,
解得:,
设,则
根据根与系数的关系得:
,
解得:,
20.(1)
(2)
(3)每顶头盔应降价20元
【分析】本题主要考查了一元二次方程的应用以及一次函数的应用,解题的关键是:根据各数量之间的关系,找出y关于x的函数关系式;根据各数量之间的关系,列式计算;找准等量关系,正确列出一元二次方程.
(1)根据利润售价进价,列出代数式即可;
(2)利用平均每周的销售量,即可找出与之间的函数关系式;
(3)利用每周的销售利润每顶的销售利润每周的销售量,可列出关于的一元二次方程,解之可求出的值,再结合降价后每顶头盔的售价不高于元,即可确定结论.
【详解】(1)解:∵进价为每顶40元,原售价为每顶68元,
∴每顶头盔降价x元后,每顶头盔的利润是元;
故答案为:;
(2)解:根据题意得:,
故答案为:;
(3)解:根据题意得:,
解得:,,
当时,,不符合题意,舍去;
当时,,符合题意.
答:每顶头盔应降价20元.
21.(1)过程见解析
(2)5
【分析】(1)先根据垂径定理得,,再根据圆周角定理得出答案;
(2)设半径是r,可知,,根据垂径定理得,再根据勾股定理列出方程,求出解即可.
【详解】(1)连接.
∵,
∴,
∴.
∵,
∴,
即;
(2)设半径是r,则,.
∵,,
∴.
在中,,
即,
解得.
所以的半径是5.
【点睛】本题主要考查了垂径定理,圆周角定理及推论,勾股定理等,勾股定理是求线段长的常用方法.
22.(1)见解析;
(2)图中阴影部分的面积是.
【分析】()由是半圆的直径,是半圆的切线,可得,即得;
()由得,可得,,即得,再利用阴影部分的面积等于半圆减去即可解题.
【详解】(1)证明:∵是半圆的直径,
∴,
∵是半圆的切线,
∴,
∴,
∴;
(2)解:由()知,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,,
∴,
∴阴影部分的面积是,
答:阴影部分的面积是.
【点睛】此题考查了圆的切线性质,含角的直角三角形的性质,圆周角定理,求扇形面积,综合运用以上知识是解题的关键.
23.(1)为等腰直角三角形
(2)证明见解析
(3),证明见解
【分析】(1)由直径所对的圆周角为可得:,再根据圆周角定理可得,再结合可得,由等角对等边可得即可解答;
(2)如图:作交的延长线于点D,因为,所以,则,所以,再证明可得,所以,则
即可;
(3)如图:延长交于点,连接,由轴对称的性质得,则,所以,,则,再根据圆周角定理可得、,最后根据勾股定理即可解答.
【详解】(1)解:,
∴
又,
,
又是该外接圆的直径
,
为等腰直角三角形
(2)解:如图:作,并延长交于点,
,
为等腰直角三角形,
,
由勾股定理可知,
,
由(1)可知为等腰直角三角形,
,
又,
,
在和中,
,
,
,
(3)解:,证明如下:
如图,延长交于点,连接,
,
为等腰直角三角形
由勾股定理可求得:,
又,
又,
,即,
为直径,
,
在Rt中,有,
.
【点睛】本题主要考查了圆周角定理、等腰直角三角形的判定与性质、全等三角形的判定与性质、轴对称的性质、勾股定理等知识点,正确地作出所需要的辅助线是解题的关键.
24.(1),
(2)
(3)七年级
【分析】本题考查了平均数,众数,中位数,方差;
(1)利用统计图中的数据可得具体的成绩,再由众数和中位数的定义进行求解即可;
(2)观察统计图,数据波动较大的对应方差较大,即可求解;
(3)由于平均数相同,中位数越大成绩越好,据此即可求解;
理解定义:“由一组数据中出现次数最多的数据是这组数据的众数;一组数据中出现次数最多的数据是这组数据的众数;将这组数据按从小到大的顺序排列,当数据的个数是奇数时,中间的数为中位数,当数据的个数是偶数时,中间两个数的平均数为中位数;一组数据方差越大波动越大,越不稳定;”,并会根据中位数的意义判断决策是解题的关键.
【详解】(1)解:由统计图得
七年级的得分情况为:分名学生,分名学生,分名学生,分名学生,
分名学生,分名学生,分名学生,
个数最多的是,
众数是分,
;
八年级的得分情况按从小到大排列为:,,,,,,,,,,
中间的两个数是,,
中位数分;
故答案:,;
(2)解:观察折线统计图可得
七年级的成绩波动明显比八年级的成绩波动大,
,
故答案:;
(3)解:由题意得
七年级和八年级的平均成绩相同,但是七年级的中位数比八年级的大,所以七年级参赛学生的成绩较好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
