2023-2024学年人教版(2012)八年级下册第二十章 数据的分析单元测试卷(含解析)
文档属性
| 名称 | 2023-2024学年人教版(2012)八年级下册第二十章 数据的分析单元测试卷(含解析) | 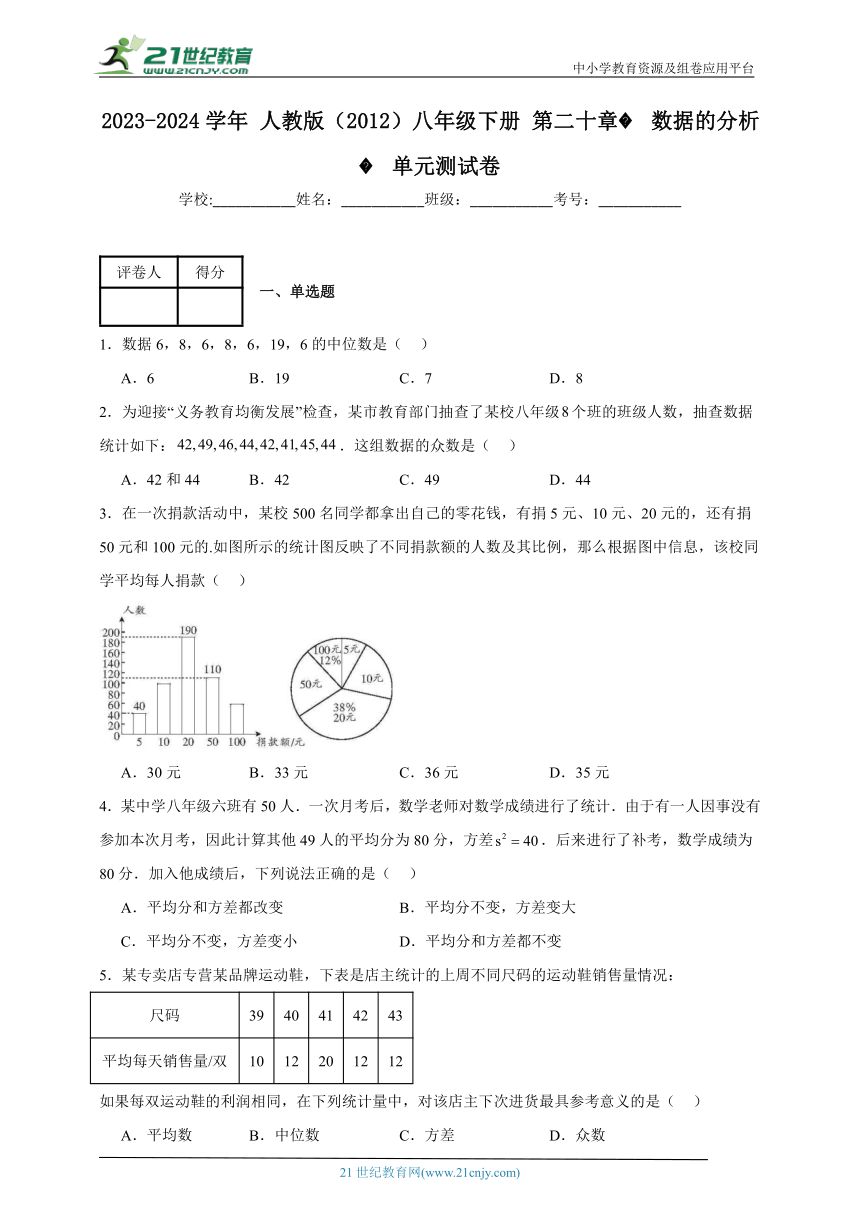 | |
| 格式 | docx | ||
| 文件大小 | 575.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:39:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年 人教版(2012)八年级下册 第二十章 数据的分析 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.数据6,8,6,8,6,19,6的中位数是( )
A.6 B.19 C.7 D.8
2.为迎接“义务教育均衡发展”检查,某市教育部门抽查了某校八年级个班的班级人数,抽查数据统计如下:.这组数据的众数是( )
A.42和44 B.42 C.49 D.44
3.在一次捐款活动中,某校500名同学都拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款额的人数及其比例,那么根据图中信息,该校同学平均每人捐款( )
A.30元 B.33元 C.36元 D.35元
4.某中学八年级六班有50人.一次月考后,数学老师对数学成绩进行了统计.由于有一人因事没有参加本次月考,因此计算其他49人的平均分为80分,方差.后来进行了补考,数学成绩为80分.加入他成绩后,下列说法正确的是( )
A.平均分和方差都改变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都不变
5.某专卖店专营某品牌运动鞋,下表是店主统计的上周不同尺码的运动鞋销售量情况:
尺码 39 40 41 42 43
平均每天销售量/双 10 12 20 12 12
如果每双运动鞋的利润相同,在下列统计量中,对该店主下次进货最具参考意义的是( )
A.平均数 B.中位数 C.方差 D.众数
6.八年级一班同学们一天的生活费用统计如图,根据统计图计算,这个班同学们一天的生活费用的平均数是( )
A.7.5元 B.15.3元 C.16.9元 D.25元
7.《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并作出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:2,4,3,2,5,2,3.则这组数据的众数和中位数分别是( )
A.2,2 B.2,2.5 C.2,3 D.3,3
8.6名同学参加体能测试,成绩如下:85,90,75,75,75,80.下列表述错误是( )
A.平均数是80 B.众数是75 C.中位数80 D.极差是15
9.小红连续5天的体温数据如下(单位:):、、、、,关于这组数据,下列说法正确的是( )
A.中位数是 B.众数是
C.平均数是 D.极差是
10.某中学七年级开展安全知识竞赛,进入决赛的学生有30名,他们的决赛成绩如表所示:
决赛成绩/分 100 99 98 97
人数 6 9 12 3
则这30名学生决赛成绩的中位数和众数分别是( ).
A.98,98 B.99,98 C.,98 D.,99
评卷人得分
二、填空题
11.在卫生检查中,各班的教室卫生成绩占,环境卫生占,个人卫生占.一班这三项成绩分别为80分,90分和90分,求该班卫生检查的总成绩是 .
12.若一组数据2,3,4,m的众数为3,则这组数据的方差是 ;
13.已知由某班40名同学的身高绘制的条形统计图如图所示,则该班同学身高的中位数是 .
14.已知一组数据5、8、10、x、7、9的众数是9,那么这组数据的中位数是 .
15.某校九年级1班50名学生的年龄情况如下(单位:岁):
年龄 14 15 16 17
人数 3 22 24 1
这个班学生年龄的中位数是 岁.
16.某单位要招聘1名英语翻译,小亮参加招聘考试的各门成绩如表所示若把听、说、读、写的成绩按计算平均成绩,则小亮的平均成绩为 .
项目 听 说 读 写
成绩(分) 70 90 85 85
评卷人得分
三、解答题
17.某射击队在一次训练中,甲、乙两名队员各射击10发子弹,成绩记录如下表;
射击次序(次) 一 二 三 四 五 六 七 八 九 十
甲的成绩(环) 8 9 7 9 8 6 7 10 8
乙的成绩(环) 6 7 9 7 9 10 8 7 7 10
经计算甲和乙的平均成绩都是8环.
(1)则表中的______;
(2)甲射击成绩的中位数、众数分别是多少?
(3)若甲成绩的方差是,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
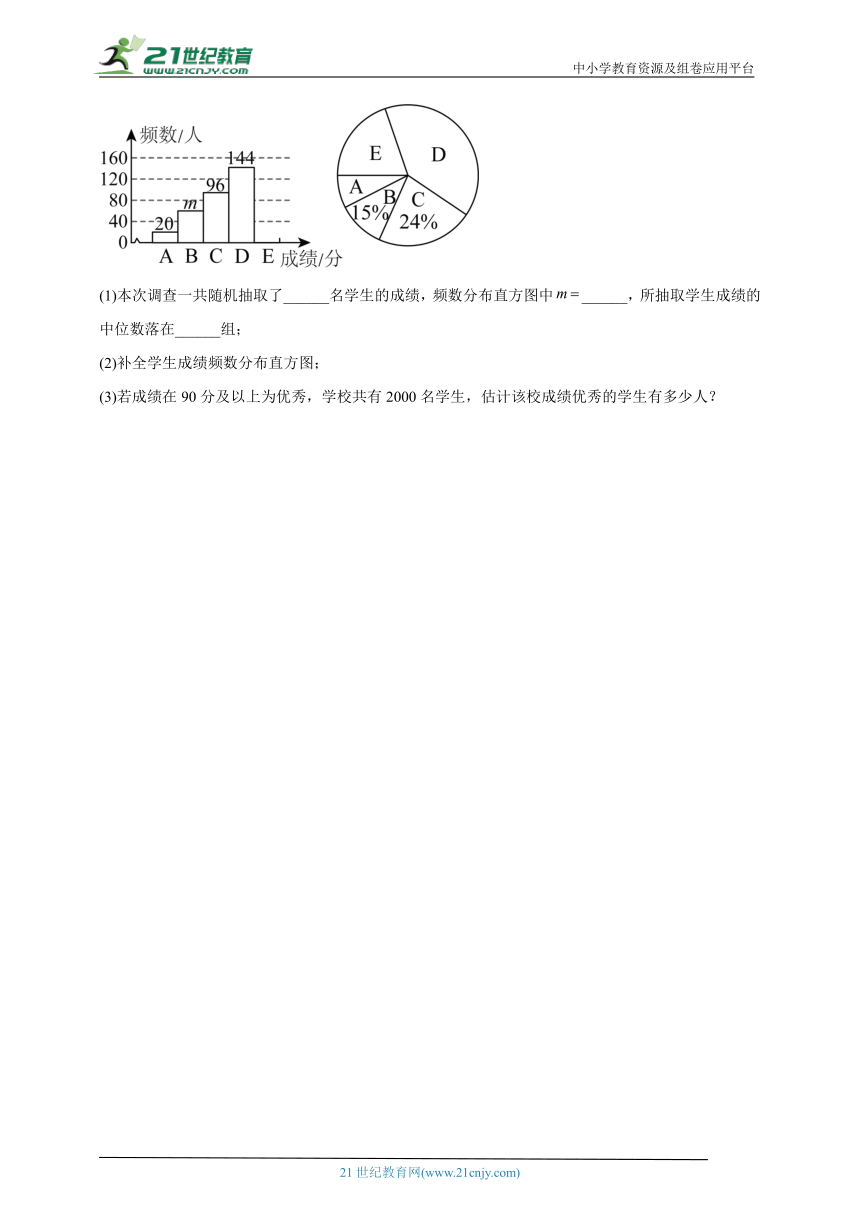
18.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:,B组:,C组:,D组:,E组:,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)本次调查一共随机抽取了______名学生的成绩,频数分布直方图中______,所抽取学生成绩的中位数落在______组;
(2)补全学生成绩频数分布直方图;
(3)若成绩在90分及以上为优秀,学校共有2000名学生,估计该校成绩优秀的学生有多少人?
参考答案:
1.A
【分析】本题考查中位数,解题的关键是熟记中位数的定义,将数据从小到大排列,奇数个数据,中间位置的就是中位数.
【详解】解:将数据6,8,6,8,6,19,6按从小到大依次排列为:
6,6,6,6,8,8,19,
位于中间位置的数为6.
∴中位数为6.
故选:A.
2.A
【解析】略
3.B
【解析】略
4.C
【分析】本题考查方差,算术平均数等知识.根据平均数,方差的定义计算即可.
【详解】解:∵补考的成绩和其他49人的平均数相同,都是80分,
该班50人的平均分为:(分),
该班50人的方差为:,
∴该班50人的测试成绩的平均分不变,方差变小,
故选:C.
5.D
【分析】此题主要考查统计的有关知识,了解平均数、中位数、众数、方差的意义是解题的关键.
【详解】解:由于众数是数据中出现次数最多的数,故该店主下次进货最具参考意义的是是众数.
故选:D.
6.C
【分析】本题考查了加权平均数的意义,解题的关键是记住加权平均数的计算公式.
【详解】解:一天的生活费用的平均数,
故选:C.
7.C
【分析】本题主要考查了众数及中位数的概念,一组数据中,出现次数最多的数为众数;按从小到大(或从大到小)顺序排列,处于中间位置的一个数(或两个数的平均数)为这组数据的中位数,根据众数及中位数的概念进行判断即可.
【详解】解:∵2出现的次数最多,
∴众数是2.
把这组数据从小到大排序为2,2,2,3,3,4,5.
∵3处于第四位的中间位置,
∴中位数是3.
故选:C.
8.C
【分析】本题考查了平均数,众数,中位数,极差;根据平均数,众数,中位数,极差的意义和计算方法逐项判断即可.
【详解】解:A.平均数是,正确;
B.∵75出现的次数最多,
∴众数是75,正确;
C.∵将数据从小到大排列为75,75,75,80,85,90,处在最中间的两个数是75,80,
∴中位数是,错误;
D.∵最大的数是90,最小的数是75,
∴极差是,正确;
故选:C.
9.B
【分析】本题考查了中位数、众数、平均数、极差,根据中位数、众数、平均数、极差的计算方法,分别求出结果即可.
【详解】解:把小红连续5天的体温从小到大排列得,、、、、,
A、中间位置的一个数是,因此中位数是,原说法错误,不符合题意;
B、出现次数最多的是,因此众数是,原说法正确,符合题意;;
C、平均数为:,原说法错误,不符合题意;
D、极差为:,原说法错误,不符合题意;
∴说法正确的是B.
故选:B.
10.C
【分析】本题考查了中位数和众数,将一组数据按大小依次排列,把处在最中间位置的一个数(或最中间位置的两个数的平均数)叫做这组数据的中位数,众数是在一组数据中出现次数最多的数据.根据众数,中位数的定义计算选择即可.
【详解】解:∵98出现的次数最多,12次,
∴众数为98;
∵中位数是第15个,16个数据的平均数,
即.
故选:C.
11.87分
【分析】本题考查了求加权平均数,根据求加权平均数的方法和步骤直接计算即可.
【详解】解:根据题意可得:
该班卫生检查的总成绩(分),
故答案为:87分.
12./
【分析】本题主要考查众数和方差,先根据众数的概念得出,再依据方差的定义计算可得.
【详解】解:∵数据2,3,4,m的众数是3,
∴,
则数据为2、3、3、4,
∴这组数据的平均数为,
∴这组数据的方差为,
故答案为:.
13.167cm
【解析】略
14.
【分析】本题考查了众数和中位数,掌握相关定义是解题关键.由众数的定义可知,,再将这组数据从小到大排列,即可就出中位数.
【详解】解:一组数据5、8、10、x、7、9的众数是9,
,
将这组数据从小到大排列:5、7、8、9、9、10,
这组数据的中位数是
故答案为:.
15.15.5
【分析】本题主要考查中位数,熟练掌握中位数的求法是解题的关键;由表格可知这个班学生年龄的中位数取第25和第26位同学的年龄的平均数,所以此题得解.
【详解】解:由题意可知这个班学生年龄的中位数为;
故答案为:15.5.
16.82分
【分析】本题考查了加权平均数,根据加权平均数公式即可求解,熟练掌握加权平均数公式是解题的关键.
【详解】解:小亮的平均成绩为:
(分).
故小亮的平均成绩为82分.
故答案为:82分.
17.(1)8
(2)中位数是8环,众数是8环
(3)甲的成绩更为稳定,理由见解析
【分析】本题主要考查了方差的定义,众数和中位数的定义,解题的关键是熟练掌握方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.一般地设n个数据,,,…的平均数为,则方差.
(1)根据甲的平均成绩为8环,然后求出a的值即可;
(2)根据中位数和众数的定义进行求解即可;
(3)先根据方差公式求出乙成绩的方差,然后再进行判断即可.
【详解】(1)解:,
故答案为:8.
(2)解:甲成绩排序后最中间的两个数据为8和8,
所以甲成绩的中位数是,
即甲射击成绩的中位数是8环,
出现次数最多的是8,
即甲射击成绩的众数是8环.
(3)解:乙成绩的方差为:
,
因为甲和乙的平均成绩都是8环,而甲成绩的方差小于乙成绩的方差,
所以甲的成绩更为稳定.
18.(1)400,60,D
(2)见解析
(3)1120名
【分析】本题主要考查调查与统计的相关知识,理解频数分布直方图、扇形统计图中的相关信息,掌握运用样本百分比估算总体数量,求中位数分方法是解题的关键.
(1)频数分布直方图中C的人数是96人,所占百分比是,由此可求出抽取的总人数;根据总体人数及B组人数占的百分比,进而求得B组人数m;根据中位数的定义,即可求出中位数落在哪一组;
(2)根据频数分布直方图中其余各组人数即可求出E组人数;
(3)根据样本所占百分比估算总体的方法即可求解.
【详解】(1)解:本次调查一共随机抽取的学生总人数为:(名),
∵B组的人数为:(名),
∴;
∵所抽取学生成绩的中位数是第200个和第201个成绩的平均数,A,B,C组的人数和为:,D组人数为,
∴所抽取学生成绩的中位数落在D组,
故答案为:400,60,D;
(2)解:E组的人数为:(人);
补全频数分布直方图如下:
;
(3)解:(名).
答:估计该校成绩优秀的学生有1120名.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年 人教版(2012)八年级下册 第二十章 数据的分析 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.数据6,8,6,8,6,19,6的中位数是( )
A.6 B.19 C.7 D.8
2.为迎接“义务教育均衡发展”检查,某市教育部门抽查了某校八年级个班的班级人数,抽查数据统计如下:.这组数据的众数是( )
A.42和44 B.42 C.49 D.44
3.在一次捐款活动中,某校500名同学都拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款额的人数及其比例,那么根据图中信息,该校同学平均每人捐款( )
A.30元 B.33元 C.36元 D.35元
4.某中学八年级六班有50人.一次月考后,数学老师对数学成绩进行了统计.由于有一人因事没有参加本次月考,因此计算其他49人的平均分为80分,方差.后来进行了补考,数学成绩为80分.加入他成绩后,下列说法正确的是( )
A.平均分和方差都改变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都不变
5.某专卖店专营某品牌运动鞋,下表是店主统计的上周不同尺码的运动鞋销售量情况:
尺码 39 40 41 42 43
平均每天销售量/双 10 12 20 12 12
如果每双运动鞋的利润相同,在下列统计量中,对该店主下次进货最具参考意义的是( )
A.平均数 B.中位数 C.方差 D.众数
6.八年级一班同学们一天的生活费用统计如图,根据统计图计算,这个班同学们一天的生活费用的平均数是( )
A.7.5元 B.15.3元 C.16.9元 D.25元
7.《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并作出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:2,4,3,2,5,2,3.则这组数据的众数和中位数分别是( )
A.2,2 B.2,2.5 C.2,3 D.3,3
8.6名同学参加体能测试,成绩如下:85,90,75,75,75,80.下列表述错误是( )
A.平均数是80 B.众数是75 C.中位数80 D.极差是15
9.小红连续5天的体温数据如下(单位:):、、、、,关于这组数据,下列说法正确的是( )
A.中位数是 B.众数是
C.平均数是 D.极差是
10.某中学七年级开展安全知识竞赛,进入决赛的学生有30名,他们的决赛成绩如表所示:
决赛成绩/分 100 99 98 97
人数 6 9 12 3
则这30名学生决赛成绩的中位数和众数分别是( ).
A.98,98 B.99,98 C.,98 D.,99
评卷人得分
二、填空题
11.在卫生检查中,各班的教室卫生成绩占,环境卫生占,个人卫生占.一班这三项成绩分别为80分,90分和90分,求该班卫生检查的总成绩是 .
12.若一组数据2,3,4,m的众数为3,则这组数据的方差是 ;
13.已知由某班40名同学的身高绘制的条形统计图如图所示,则该班同学身高的中位数是 .
14.已知一组数据5、8、10、x、7、9的众数是9,那么这组数据的中位数是 .
15.某校九年级1班50名学生的年龄情况如下(单位:岁):
年龄 14 15 16 17
人数 3 22 24 1
这个班学生年龄的中位数是 岁.
16.某单位要招聘1名英语翻译,小亮参加招聘考试的各门成绩如表所示若把听、说、读、写的成绩按计算平均成绩,则小亮的平均成绩为 .
项目 听 说 读 写
成绩(分) 70 90 85 85
评卷人得分
三、解答题
17.某射击队在一次训练中,甲、乙两名队员各射击10发子弹,成绩记录如下表;
射击次序(次) 一 二 三 四 五 六 七 八 九 十
甲的成绩(环) 8 9 7 9 8 6 7 10 8
乙的成绩(环) 6 7 9 7 9 10 8 7 7 10
经计算甲和乙的平均成绩都是8环.
(1)则表中的______;
(2)甲射击成绩的中位数、众数分别是多少?
(3)若甲成绩的方差是,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
18.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:,B组:,C组:,D组:,E组:,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)本次调查一共随机抽取了______名学生的成绩,频数分布直方图中______,所抽取学生成绩的中位数落在______组;
(2)补全学生成绩频数分布直方图;
(3)若成绩在90分及以上为优秀,学校共有2000名学生,估计该校成绩优秀的学生有多少人?
参考答案:
1.A
【分析】本题考查中位数,解题的关键是熟记中位数的定义,将数据从小到大排列,奇数个数据,中间位置的就是中位数.
【详解】解:将数据6,8,6,8,6,19,6按从小到大依次排列为:
6,6,6,6,8,8,19,
位于中间位置的数为6.
∴中位数为6.
故选:A.
2.A
【解析】略
3.B
【解析】略
4.C
【分析】本题考查方差,算术平均数等知识.根据平均数,方差的定义计算即可.
【详解】解:∵补考的成绩和其他49人的平均数相同,都是80分,
该班50人的平均分为:(分),
该班50人的方差为:,
∴该班50人的测试成绩的平均分不变,方差变小,
故选:C.
5.D
【分析】此题主要考查统计的有关知识,了解平均数、中位数、众数、方差的意义是解题的关键.
【详解】解:由于众数是数据中出现次数最多的数,故该店主下次进货最具参考意义的是是众数.
故选:D.
6.C
【分析】本题考查了加权平均数的意义,解题的关键是记住加权平均数的计算公式.
【详解】解:一天的生活费用的平均数,
故选:C.
7.C
【分析】本题主要考查了众数及中位数的概念,一组数据中,出现次数最多的数为众数;按从小到大(或从大到小)顺序排列,处于中间位置的一个数(或两个数的平均数)为这组数据的中位数,根据众数及中位数的概念进行判断即可.
【详解】解:∵2出现的次数最多,
∴众数是2.
把这组数据从小到大排序为2,2,2,3,3,4,5.
∵3处于第四位的中间位置,
∴中位数是3.
故选:C.
8.C
【分析】本题考查了平均数,众数,中位数,极差;根据平均数,众数,中位数,极差的意义和计算方法逐项判断即可.
【详解】解:A.平均数是,正确;
B.∵75出现的次数最多,
∴众数是75,正确;
C.∵将数据从小到大排列为75,75,75,80,85,90,处在最中间的两个数是75,80,
∴中位数是,错误;
D.∵最大的数是90,最小的数是75,
∴极差是,正确;
故选:C.
9.B
【分析】本题考查了中位数、众数、平均数、极差,根据中位数、众数、平均数、极差的计算方法,分别求出结果即可.
【详解】解:把小红连续5天的体温从小到大排列得,、、、、,
A、中间位置的一个数是,因此中位数是,原说法错误,不符合题意;
B、出现次数最多的是,因此众数是,原说法正确,符合题意;;
C、平均数为:,原说法错误,不符合题意;
D、极差为:,原说法错误,不符合题意;
∴说法正确的是B.
故选:B.
10.C
【分析】本题考查了中位数和众数,将一组数据按大小依次排列,把处在最中间位置的一个数(或最中间位置的两个数的平均数)叫做这组数据的中位数,众数是在一组数据中出现次数最多的数据.根据众数,中位数的定义计算选择即可.
【详解】解:∵98出现的次数最多,12次,
∴众数为98;
∵中位数是第15个,16个数据的平均数,
即.
故选:C.
11.87分
【分析】本题考查了求加权平均数,根据求加权平均数的方法和步骤直接计算即可.
【详解】解:根据题意可得:
该班卫生检查的总成绩(分),
故答案为:87分.
12./
【分析】本题主要考查众数和方差,先根据众数的概念得出,再依据方差的定义计算可得.
【详解】解:∵数据2,3,4,m的众数是3,
∴,
则数据为2、3、3、4,
∴这组数据的平均数为,
∴这组数据的方差为,
故答案为:.
13.167cm
【解析】略
14.
【分析】本题考查了众数和中位数,掌握相关定义是解题关键.由众数的定义可知,,再将这组数据从小到大排列,即可就出中位数.
【详解】解:一组数据5、8、10、x、7、9的众数是9,
,
将这组数据从小到大排列:5、7、8、9、9、10,
这组数据的中位数是
故答案为:.
15.15.5
【分析】本题主要考查中位数,熟练掌握中位数的求法是解题的关键;由表格可知这个班学生年龄的中位数取第25和第26位同学的年龄的平均数,所以此题得解.
【详解】解:由题意可知这个班学生年龄的中位数为;
故答案为:15.5.
16.82分
【分析】本题考查了加权平均数,根据加权平均数公式即可求解,熟练掌握加权平均数公式是解题的关键.
【详解】解:小亮的平均成绩为:
(分).
故小亮的平均成绩为82分.
故答案为:82分.
17.(1)8
(2)中位数是8环,众数是8环
(3)甲的成绩更为稳定,理由见解析
【分析】本题主要考查了方差的定义,众数和中位数的定义,解题的关键是熟练掌握方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.一般地设n个数据,,,…的平均数为,则方差.
(1)根据甲的平均成绩为8环,然后求出a的值即可;
(2)根据中位数和众数的定义进行求解即可;
(3)先根据方差公式求出乙成绩的方差,然后再进行判断即可.
【详解】(1)解:,
故答案为:8.
(2)解:甲成绩排序后最中间的两个数据为8和8,
所以甲成绩的中位数是,
即甲射击成绩的中位数是8环,
出现次数最多的是8,
即甲射击成绩的众数是8环.
(3)解:乙成绩的方差为:
,
因为甲和乙的平均成绩都是8环,而甲成绩的方差小于乙成绩的方差,
所以甲的成绩更为稳定.
18.(1)400,60,D
(2)见解析
(3)1120名
【分析】本题主要考查调查与统计的相关知识,理解频数分布直方图、扇形统计图中的相关信息,掌握运用样本百分比估算总体数量,求中位数分方法是解题的关键.
(1)频数分布直方图中C的人数是96人,所占百分比是,由此可求出抽取的总人数;根据总体人数及B组人数占的百分比,进而求得B组人数m;根据中位数的定义,即可求出中位数落在哪一组;
(2)根据频数分布直方图中其余各组人数即可求出E组人数;
(3)根据样本所占百分比估算总体的方法即可求解.
【详解】(1)解:本次调查一共随机抽取的学生总人数为:(名),
∵B组的人数为:(名),
∴;
∵所抽取学生成绩的中位数是第200个和第201个成绩的平均数,A,B,C组的人数和为:,D组人数为,
∴所抽取学生成绩的中位数落在D组,
故答案为:400,60,D;
(2)解:E组的人数为:(人);
补全频数分布直方图如下:
;
(3)解:(名).
答:估计该校成绩优秀的学生有1120名.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
