2023-2024学年人教版(2012)八年级下册第十八章平行四边形单元测试卷(含解析)
文档属性
| 名称 | 2023-2024学年人教版(2012)八年级下册第十八章平行四边形单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:39:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2023-2024学年 人教版(2012)八年级下册 第十八章 平行四边形 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
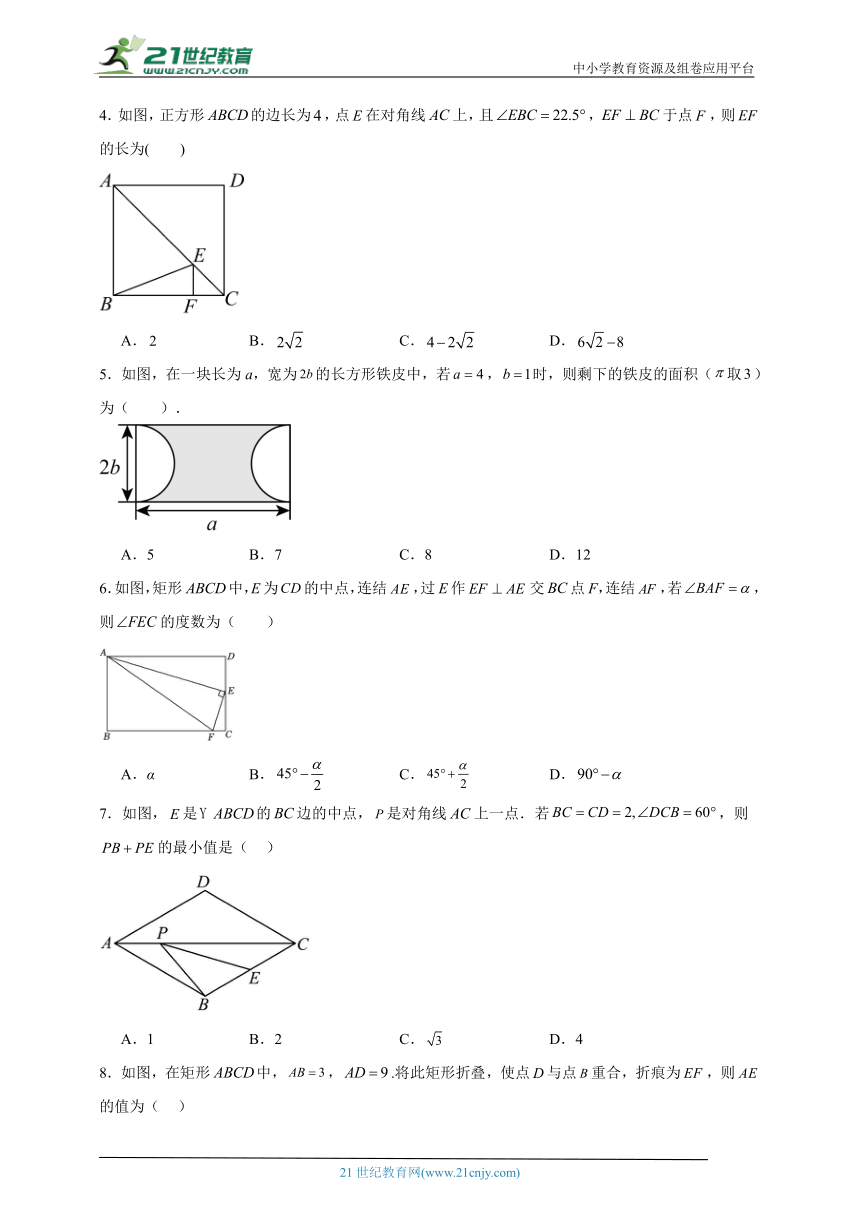
1.如图,在矩形中,平分交于点E,连接,若,,则的长为( )
A. B. C. D.
2.如图,中,,,分别是其角平分线和中线,过点C作于点F,交于点G,连接,则①;②;③;④.其中正确的是( )
A.①②③④ B.①② C.②③④ D.①③④
3.如图,将长方形纸片的角C沿着折叠(点F在上,不与B,C重合),使点C落在长方形内部点E处,若平分,则的度数α是( )
A. B.
C. D.α随折痕位置的变化而变化
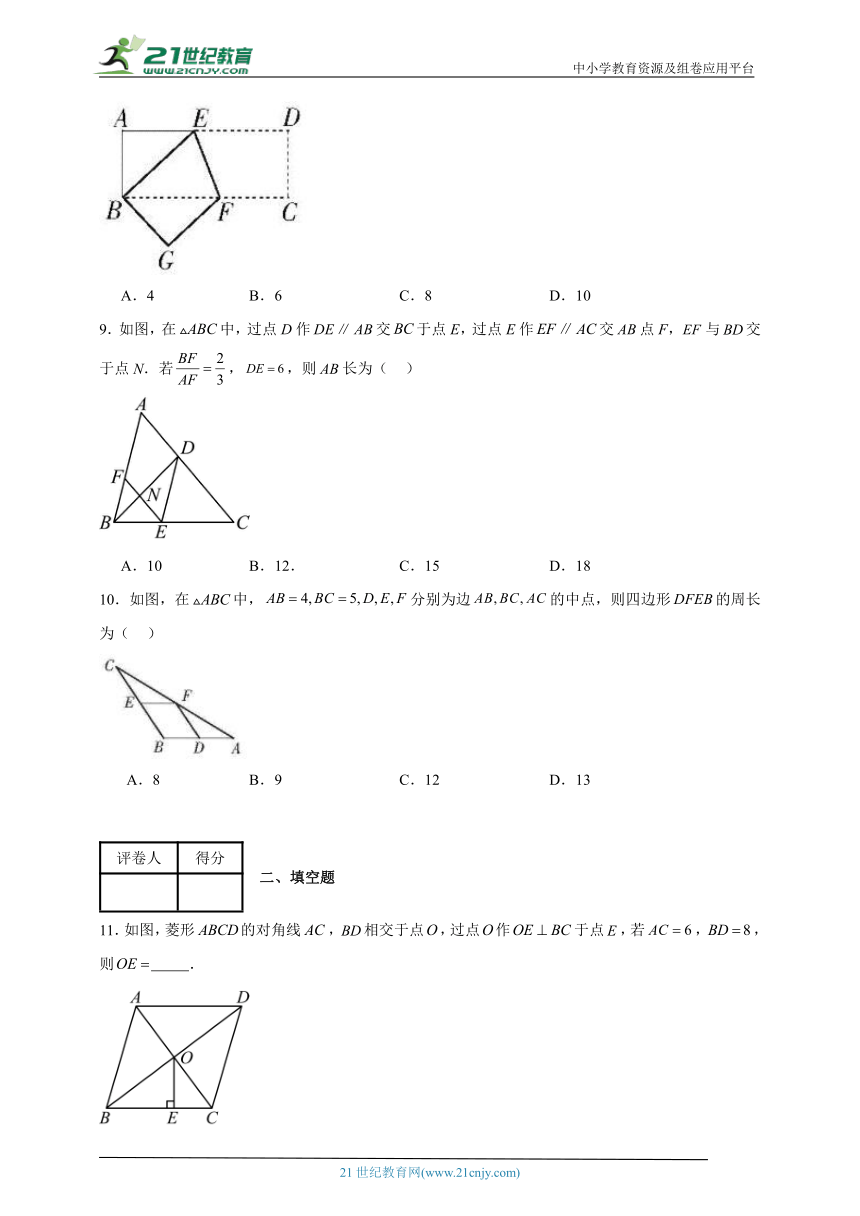
4.如图,正方形的边长为,点在对角线上,且,于点,则的长为( )
A. B. C. D.
5.如图,在一块长为a,宽为的长方形铁皮中,若,时,则剩下的铁皮的面积(取)为( ).
A.5 B.7 C.8 D.12
6.如图,矩形中,E为的中点,连结,过E作交点F,连结,若,则的度数为( )
A.α B. C. D.
7.如图,是的边的中点,是对角线上一点.若,则的最小值是( )
A.1 B.2 C. D.4
8.如图,在矩形中,,.将此矩形折叠,使点与点重合,折痕为,则的值为( )
A.4 B.6 C.8 D.10
9.如图,在中,过点D作交于点E,过点E作交点F,与交于点N.若,,则长为( )
A.10 B.12. C.15 D.18
10.如图,在中,分别为边的中点,则四边形的周长为( )
A.8 B.9 C.12 D.13
评卷人得分
二、填空题
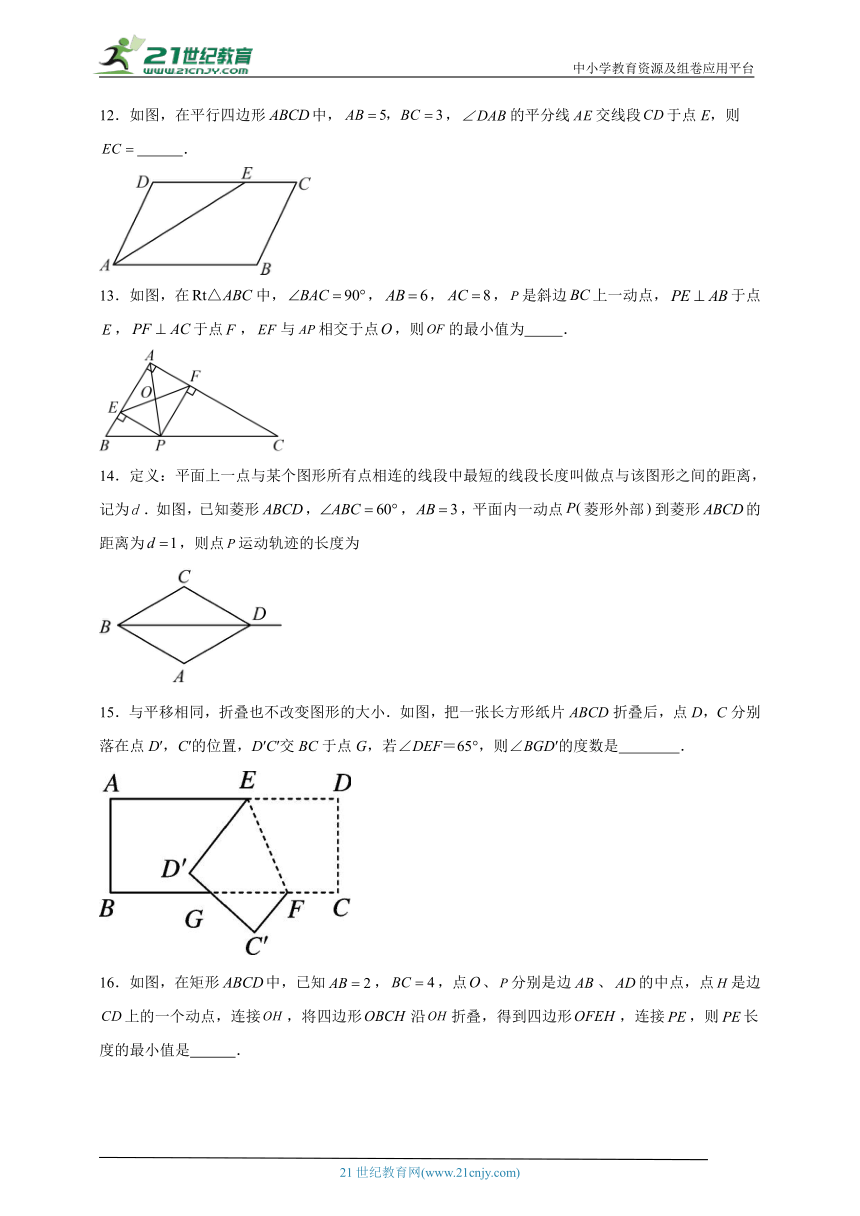
11.如图,菱形的对角线,相交于点,过点作于点,若,,则 .
12.如图,在平行四边形中,,的平分线交线段于点E,则 .
13.如图,在中,,,,是斜边上一动点,于点,于点,与相交于点,则的最小值为 .
14.定义:平面上一点与某个图形所有点相连的线段中最短的线段长度叫做点与该图形之间的距离,记为.如图,已知菱形,,,平面内一动点菱形外部到菱形的距离为,则点运动轨迹的长度为
15.与平移相同,折叠也不改变图形的大小.如图,把一张长方形纸片ABCD折叠后,点D,C分别落在点D′,C′的位置,D′C′交BC于点G,若∠DEF=65°,则∠BGD′的度数是 .
16.如图,在矩形中,已知,,点、分别是边、的中点,点是边上的一个动点,连接,将四边形沿折叠,得到四边形,连接,则长度的最小值是 .
评卷人得分
三、解答题
17.如图, 中,,在BC的延长线上取一点D,使得,点E是的中点,连接,M为的中点,连接、.
(1)试判断与的位置关系,并说明理由;
(2)若,请求出的度数.
18.如图,在菱形中,对角线,交延长线于E,交延长线于点F.
(1)求证:四边形是矩形;
(2)连接,若,,求线段的长.
参考答案:
1.C
【分析】本题考查矩形的性质,勾股定理及等角对等边,根据矩形得到,,,从而得到,根据角平分线得到,从而得到,即可得到,结合勾股定理即可得到答案;
【详解】解:∵四边形是矩形,,,
∴,,,,
∴,
∵平分,
∴,
,
∴,
∴,
在中,
,
故选:C.
2.A
【分析】由角平分线的定义可得出,即易证,得出,再根据中线的定义结合三角形中位线定理即可得出,故①正确;由全等三角形的性质可得出,结合三角形外角的性质可得出,最后根据,即可得出,故②正确;由全等三角形的性质可得出,进而得出,结合三角形中位线定理即可得出,故③正确;由题意可确定,即得出,从而得出.延长到M,使,连接.易证,即得出.由三角形三边关系可得出,即可证明,故④正确.
【详解】解:∵平分,
∴.
∵,
∴.
在和中,,
∴,
∴.
∵为的中线,
∴,
∴,故①正确;
∵,
∴,
∵,
∴,
∴,
∴,
∴,故②正确;
∵,
∴,
∴,
∵F、E分别是的中点,
∴,
∴,故③正确;
∵,
∴,
∵,
∴,
∴.
∵,
∴.
延长到M,使,连接.
∵在和中,,
∴,
∴.
在中,,
∵,
∴,
∴,
∴,故④正确.
综上可知正确的是①②③④.
故选A.
【点睛】本题考查角平分线的定义,三角形中线的性质,三角形中位线的判定和性质,三角形全等的判定和性质,三角形三边关系等知识.熟练掌握上述知识,并正确作出辅助线构造全等三角形是解题关键.
3.C
【分析】本题考查了折叠的性质,角的平分线的定义,平角的定义,熟练掌握折叠的性质是解题的关键.
【详解】∵且平分,
∴
.
故选:C.
4.C
【分析】本题考查了正方形的性质,勾股定理,等腰三角形的判定和性质,根据正方形的性质得到,,求得,根据等腰三角形的判定定理得到,推出是等腰直角三角形,于是得到结论.
【详解】解:四边形是正方形,
,,
正方形的边长为,
,
,,
,
,
,
,
,
,
,
是等腰直角三角形,
,
故选:C.
5.A
【分析】本题主要考查求不规则图形面积,解答本题的关键在于将不规则图形转化为规则图形面积再去求解即可.
【详解】解:剩下的铁皮的面积=长方形的面积﹣圆的面积,
故选:A.
6.B
【分析】本题考查了矩形的性质,全等三角形的判定和性质,线段垂直平分线的性质,添加合适的辅助线构造全等三角形是解题的关键.延长,交的延长线于点G,根据矩形的性质可得,,,可证,根据全等三角形的性质可得,可知垂直平分,根据线段垂直平分线的性质可得,进一步可得,根据,可得,可表示出的度数,进一步可得的度数,再根据,可得的度数.
【详解】解:如图:延长,交的延长线于点G,
∵四边形是矩形
∴,,
∴
∵E为边中点,
∴
在和中
∴
∴
∵
∴垂直平分
∴,
∵
∴
∴
∵
∴
∵
∴
∴
故选:B
7.C
【分析】本题主要考查轴对称-最短路线问题,菱形的判定与性质,勾股定理等知识点.找出B点关于的对称点D,连接交于P,则就是的最小值,求出即可.
【详解】解:∵四边形是平行四边形,,
∴是菱形,
连接,交于O,连接交于P,
由菱形的对角线互相垂直平分,可得B、D关于对称,则,
∴,
即就是的最小值.
∵四边形是菱形,
∴,,
∴是等边三角形,
∵,
∴.
在中,.
即的最小值为.
故选:C.
8.A
【解析】略
9.A
【分析】本题考查平行四边形的判定与性质,证明四边形是平行四边形,得到,然后由,求得,即可求解.
【详解】解:∵,,
∴四边形是平行四边形,
∴,
∵
∴
∴
故选:A.
10.B
【解析】略
11.//
【分析】本题考查菱形的性质及勾股定理,由菱形中,,,可求得的长,由面积法可求的长;
【详解】解:∵由菱形中,,,
∴,,,
∴,
∵,
∴,
故答案为:.
12.2
【分析】本题考查平行四边形的性质,平行线的性质,等腰三角形的判定和性质等知识.由平行四边形的性质结合题意间接证明是解题关键.由平行四边形的性质可得出,从而可证,结合题意得出,即证明,最后由求解即可.
【详解】解:∵四边形为平行四边形,
∴,,,
∴.
∵为的平分线,
∴,
∴,
∴,
∴.
故答案为:2.
13.
【分析】本题考查了矩形的性质的运用,勾股定理的运用,三角形的面积公式的运用,垂线段最短的性质的运用,根据,,结合,即可判断四边形是矩形, 根据矩形的对角线相等,于是可知当最小时,也最小,即当时,最小,最小,解题的关键求出的最小值是关键.
【详解】∵,,
∴,
∵,
∴四边形是矩形,
∴,,
∴当最小时,最小,最小,即当时,
∵,,
∴,
∴,
∴,
∴线段的最小值为,
∴线段的最小值为,
故答案为:.
14./
【分析】本题考查了菱形的性质,圆的周长公式,根据新定义可得点运动轨迹的长度为菱形的边长加上一个圆的周长,即可求解.
【详解】解:如图所示,依题意点运动轨迹的长度为菱形的边长加上一个圆的周长,
依题意, 点运动轨迹的长度为,
故答案为:.
15.40°
【解析】略
16./
【分析】本题考查了矩形的性质、折叠性质、勾股定理、三角形的三边关系,连接、,根据矩形和折叠性质,结合勾股定理求得,,再根据三角形的三边关系求解即可.熟练掌握折叠性质和三角形的三边关系求最值是解答的关键.
【详解】解:连接、,
∵四边形是矩形,,
∴,,
∵点、分别是边、的中点,
∴,,
∴,
由折叠性质得,,,
∴,
∵,
当点O、P、E共线时取等号,长度的最小值是,
故答案为:.
17.(1),理由见解析
(2)
【分析】此题考查了直角三角形斜边的中线性质,熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.
(1)根据直角三角形的性质推出,根据等腰三角形的性质即可得结果;
(2)根据直角三角形的性质推出,根据等腰三角形的性质推出,,根据三角形外角性质求出,,求出、,
【详解】(1)
理由如下:连接
,点E是的中点,
,
,
M为的中点,
.
(2),点E是的中点,
.
由(1)知:,
.
设,
则.
,
.
解得:.
.
.
18.(1)见解析
(2)
【分析】(1)本题主要考查特殊平行四边形的判定,根据是菱形可得边长平行,再根据已知判定为平行四边形,再根据垂直即可判定为矩形,解答本题的关键在于熟练掌握矩形的判定条件.
(2)本题主要考查了矩形的性质,根据矩形对角线平分且相等可求得,再运用勾股定理求出与,结合矩形的性质即可求出,解答本题的关键在于熟练掌握矩的性质.
【详解】(1)证明:∵四边形是菱形,
∴,即,
∵又,
∴四边形是平行四边形(两组对边分别平行的四边形是平行四边形),
又∵,
∴平行四边形是矩形(有一个角是直角的平行四边形是矩形).
(2)解:如图所示:
∵四边形ABCD为菱形,
∴,
又∵四边形为矩形,
,
又,
,
∴.
在中,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年 人教版(2012)八年级下册 第十八章 平行四边形 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,在矩形中,平分交于点E,连接,若,,则的长为( )
A. B. C. D.
2.如图,中,,,分别是其角平分线和中线,过点C作于点F,交于点G,连接,则①;②;③;④.其中正确的是( )
A.①②③④ B.①② C.②③④ D.①③④
3.如图,将长方形纸片的角C沿着折叠(点F在上,不与B,C重合),使点C落在长方形内部点E处,若平分,则的度数α是( )
A. B.
C. D.α随折痕位置的变化而变化
4.如图,正方形的边长为,点在对角线上,且,于点,则的长为( )
A. B. C. D.
5.如图,在一块长为a,宽为的长方形铁皮中,若,时,则剩下的铁皮的面积(取)为( ).
A.5 B.7 C.8 D.12
6.如图,矩形中,E为的中点,连结,过E作交点F,连结,若,则的度数为( )
A.α B. C. D.
7.如图,是的边的中点,是对角线上一点.若,则的最小值是( )
A.1 B.2 C. D.4
8.如图,在矩形中,,.将此矩形折叠,使点与点重合,折痕为,则的值为( )
A.4 B.6 C.8 D.10
9.如图,在中,过点D作交于点E,过点E作交点F,与交于点N.若,,则长为( )
A.10 B.12. C.15 D.18
10.如图,在中,分别为边的中点,则四边形的周长为( )
A.8 B.9 C.12 D.13
评卷人得分
二、填空题
11.如图,菱形的对角线,相交于点,过点作于点,若,,则 .
12.如图,在平行四边形中,,的平分线交线段于点E,则 .
13.如图,在中,,,,是斜边上一动点,于点,于点,与相交于点,则的最小值为 .
14.定义:平面上一点与某个图形所有点相连的线段中最短的线段长度叫做点与该图形之间的距离,记为.如图,已知菱形,,,平面内一动点菱形外部到菱形的距离为,则点运动轨迹的长度为
15.与平移相同,折叠也不改变图形的大小.如图,把一张长方形纸片ABCD折叠后,点D,C分别落在点D′,C′的位置,D′C′交BC于点G,若∠DEF=65°,则∠BGD′的度数是 .
16.如图,在矩形中,已知,,点、分别是边、的中点,点是边上的一个动点,连接,将四边形沿折叠,得到四边形,连接,则长度的最小值是 .
评卷人得分
三、解答题
17.如图, 中,,在BC的延长线上取一点D,使得,点E是的中点,连接,M为的中点,连接、.
(1)试判断与的位置关系,并说明理由;
(2)若,请求出的度数.
18.如图,在菱形中,对角线,交延长线于E,交延长线于点F.
(1)求证:四边形是矩形;
(2)连接,若,,求线段的长.
参考答案:
1.C
【分析】本题考查矩形的性质,勾股定理及等角对等边,根据矩形得到,,,从而得到,根据角平分线得到,从而得到,即可得到,结合勾股定理即可得到答案;
【详解】解:∵四边形是矩形,,,
∴,,,,
∴,
∵平分,
∴,
,
∴,
∴,
在中,
,
故选:C.
2.A
【分析】由角平分线的定义可得出,即易证,得出,再根据中线的定义结合三角形中位线定理即可得出,故①正确;由全等三角形的性质可得出,结合三角形外角的性质可得出,最后根据,即可得出,故②正确;由全等三角形的性质可得出,进而得出,结合三角形中位线定理即可得出,故③正确;由题意可确定,即得出,从而得出.延长到M,使,连接.易证,即得出.由三角形三边关系可得出,即可证明,故④正确.
【详解】解:∵平分,
∴.
∵,
∴.
在和中,,
∴,
∴.
∵为的中线,
∴,
∴,故①正确;
∵,
∴,
∵,
∴,
∴,
∴,
∴,故②正确;
∵,
∴,
∴,
∵F、E分别是的中点,
∴,
∴,故③正确;
∵,
∴,
∵,
∴,
∴.
∵,
∴.
延长到M,使,连接.
∵在和中,,
∴,
∴.
在中,,
∵,
∴,
∴,
∴,故④正确.
综上可知正确的是①②③④.
故选A.
【点睛】本题考查角平分线的定义,三角形中线的性质,三角形中位线的判定和性质,三角形全等的判定和性质,三角形三边关系等知识.熟练掌握上述知识,并正确作出辅助线构造全等三角形是解题关键.
3.C
【分析】本题考查了折叠的性质,角的平分线的定义,平角的定义,熟练掌握折叠的性质是解题的关键.
【详解】∵且平分,
∴
.
故选:C.
4.C
【分析】本题考查了正方形的性质,勾股定理,等腰三角形的判定和性质,根据正方形的性质得到,,求得,根据等腰三角形的判定定理得到,推出是等腰直角三角形,于是得到结论.
【详解】解:四边形是正方形,
,,
正方形的边长为,
,
,,
,
,
,
,
,
,
,
是等腰直角三角形,
,
故选:C.
5.A
【分析】本题主要考查求不规则图形面积,解答本题的关键在于将不规则图形转化为规则图形面积再去求解即可.
【详解】解:剩下的铁皮的面积=长方形的面积﹣圆的面积,
故选:A.
6.B
【分析】本题考查了矩形的性质,全等三角形的判定和性质,线段垂直平分线的性质,添加合适的辅助线构造全等三角形是解题的关键.延长,交的延长线于点G,根据矩形的性质可得,,,可证,根据全等三角形的性质可得,可知垂直平分,根据线段垂直平分线的性质可得,进一步可得,根据,可得,可表示出的度数,进一步可得的度数,再根据,可得的度数.
【详解】解:如图:延长,交的延长线于点G,
∵四边形是矩形
∴,,
∴
∵E为边中点,
∴
在和中
∴
∴
∵
∴垂直平分
∴,
∵
∴
∴
∵
∴
∵
∴
∴
故选:B
7.C
【分析】本题主要考查轴对称-最短路线问题,菱形的判定与性质,勾股定理等知识点.找出B点关于的对称点D,连接交于P,则就是的最小值,求出即可.
【详解】解:∵四边形是平行四边形,,
∴是菱形,
连接,交于O,连接交于P,
由菱形的对角线互相垂直平分,可得B、D关于对称,则,
∴,
即就是的最小值.
∵四边形是菱形,
∴,,
∴是等边三角形,
∵,
∴.
在中,.
即的最小值为.
故选:C.
8.A
【解析】略
9.A
【分析】本题考查平行四边形的判定与性质,证明四边形是平行四边形,得到,然后由,求得,即可求解.
【详解】解:∵,,
∴四边形是平行四边形,
∴,
∵
∴
∴
故选:A.
10.B
【解析】略
11.//
【分析】本题考查菱形的性质及勾股定理,由菱形中,,,可求得的长,由面积法可求的长;
【详解】解:∵由菱形中,,,
∴,,,
∴,
∵,
∴,
故答案为:.
12.2
【分析】本题考查平行四边形的性质,平行线的性质,等腰三角形的判定和性质等知识.由平行四边形的性质结合题意间接证明是解题关键.由平行四边形的性质可得出,从而可证,结合题意得出,即证明,最后由求解即可.
【详解】解:∵四边形为平行四边形,
∴,,,
∴.
∵为的平分线,
∴,
∴,
∴,
∴.
故答案为:2.
13.
【分析】本题考查了矩形的性质的运用,勾股定理的运用,三角形的面积公式的运用,垂线段最短的性质的运用,根据,,结合,即可判断四边形是矩形, 根据矩形的对角线相等,于是可知当最小时,也最小,即当时,最小,最小,解题的关键求出的最小值是关键.
【详解】∵,,
∴,
∵,
∴四边形是矩形,
∴,,
∴当最小时,最小,最小,即当时,
∵,,
∴,
∴,
∴,
∴线段的最小值为,
∴线段的最小值为,
故答案为:.
14./
【分析】本题考查了菱形的性质,圆的周长公式,根据新定义可得点运动轨迹的长度为菱形的边长加上一个圆的周长,即可求解.
【详解】解:如图所示,依题意点运动轨迹的长度为菱形的边长加上一个圆的周长,
依题意, 点运动轨迹的长度为,
故答案为:.
15.40°
【解析】略
16./
【分析】本题考查了矩形的性质、折叠性质、勾股定理、三角形的三边关系,连接、,根据矩形和折叠性质,结合勾股定理求得,,再根据三角形的三边关系求解即可.熟练掌握折叠性质和三角形的三边关系求最值是解答的关键.
【详解】解:连接、,
∵四边形是矩形,,
∴,,
∵点、分别是边、的中点,
∴,,
∴,
由折叠性质得,,,
∴,
∵,
当点O、P、E共线时取等号,长度的最小值是,
故答案为:.
17.(1),理由见解析
(2)
【分析】此题考查了直角三角形斜边的中线性质,熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.
(1)根据直角三角形的性质推出,根据等腰三角形的性质即可得结果;
(2)根据直角三角形的性质推出,根据等腰三角形的性质推出,,根据三角形外角性质求出,,求出、,
【详解】(1)
理由如下:连接
,点E是的中点,
,
,
M为的中点,
.
(2),点E是的中点,
.
由(1)知:,
.
设,
则.
,
.
解得:.
.
.
18.(1)见解析
(2)
【分析】(1)本题主要考查特殊平行四边形的判定,根据是菱形可得边长平行,再根据已知判定为平行四边形,再根据垂直即可判定为矩形,解答本题的关键在于熟练掌握矩形的判定条件.
(2)本题主要考查了矩形的性质,根据矩形对角线平分且相等可求得,再运用勾股定理求出与,结合矩形的性质即可求出,解答本题的关键在于熟练掌握矩的性质.
【详解】(1)证明:∵四边形是菱形,
∴,即,
∵又,
∴四边形是平行四边形(两组对边分别平行的四边形是平行四边形),
又∵,
∴平行四边形是矩形(有一个角是直角的平行四边形是矩形).
(2)解:如图所示:
∵四边形ABCD为菱形,
∴,
又∵四边形为矩形,
,
又,
,
∴.
在中,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
