2023-2024学年人教版(2012)九年级下册第二十九章 投影与视图单元测试卷(含解析)
文档属性
| 名称 | 2023-2024学年人教版(2012)九年级下册第二十九章 投影与视图单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 785.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:48:38 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2023-2024学年 人教版(2012)九年级下册 第二十九章 投影与视图 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图是由一些相同的小正方体构成的几何体的左视图和俯视图,这些相同的小正方体的个数为( )
A.5个 B.6个 C.7个 D.8个
2.下列几何体中,其主视图、左视图、右视图完全相同的是( )
A. B. C. D.
3.兴趣小组测量学校的旗杆,在阳光下,甲同学测得长1米的竹竿影长为米,同一时刻乙同学测量时发现旗杆的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,墙壁垂直地面,如图所示,落在墙上的影长为2米,,落在地面上的影长AB为9米,则旗杆的高度是( )米.
A.8 B.12 C. D.
4.如图,小树在路灯O的照射下形成投影.若树高,树影,树与路灯的水平距离.则路灯的高度为( )
A. B. C. D.
5.如图,是一个由6个大小相同的正方体组成的几何体,从正面看这个几何体,得到的图形是( )
A. B.
C. D.
6.中午12点,身高为的小冰的影长为,同学小雪此时在同一地点的影长为,那么小雪的身高为( ).
A. B. C. D.
7.如图是由个相同的小立方块搭成的几何体,那么这个几何体的左视图是( )
A. B. C. D.
8.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为 ( )
A. B. C. D.
9.如图是一个由4个相同的小正方形组成的立体图形,它的左视图是( )
A. B. C. D.
10.由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示,则搭成这个几何体的小正方体的个数最多为( )
A.3个 B.4个 C.5个 D.不能确定
评卷人得分
二、填空题
11.如图所示的几何体由若干个相同的小正方体搭成,要保持从上面和左面看到的形状图不变,最多可以同时拿走 个小正方体.
12.由若干个边长为的小正方体搭成一个组合体,它的主视图、左视图都是如图所示的形状,设垒成这种几何体所需小正方体的个数最少为,最多为,则的值为 .
13.古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔塔顶的影子处直立一根木杆,借助太阳光测金字塔的高度.如图所示,木杆长米.它的影长是米,同一时刻测得是米,则金字塔的高度是 米.
14.如图所示的是从不同方向观察一个长方体得到的视图,则左视图的面积为 .
15.如图,小阳发现电线杆 的影子落在土坡的坡面 和地面 上,量得 米,米,的坡度为:;且此时测得 米杆在地面上的影长为 米,则电线杆的高度为 米.
16.一个几何体由若干个大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是用 个小立方块搭成的.
评卷人得分
三、解答题
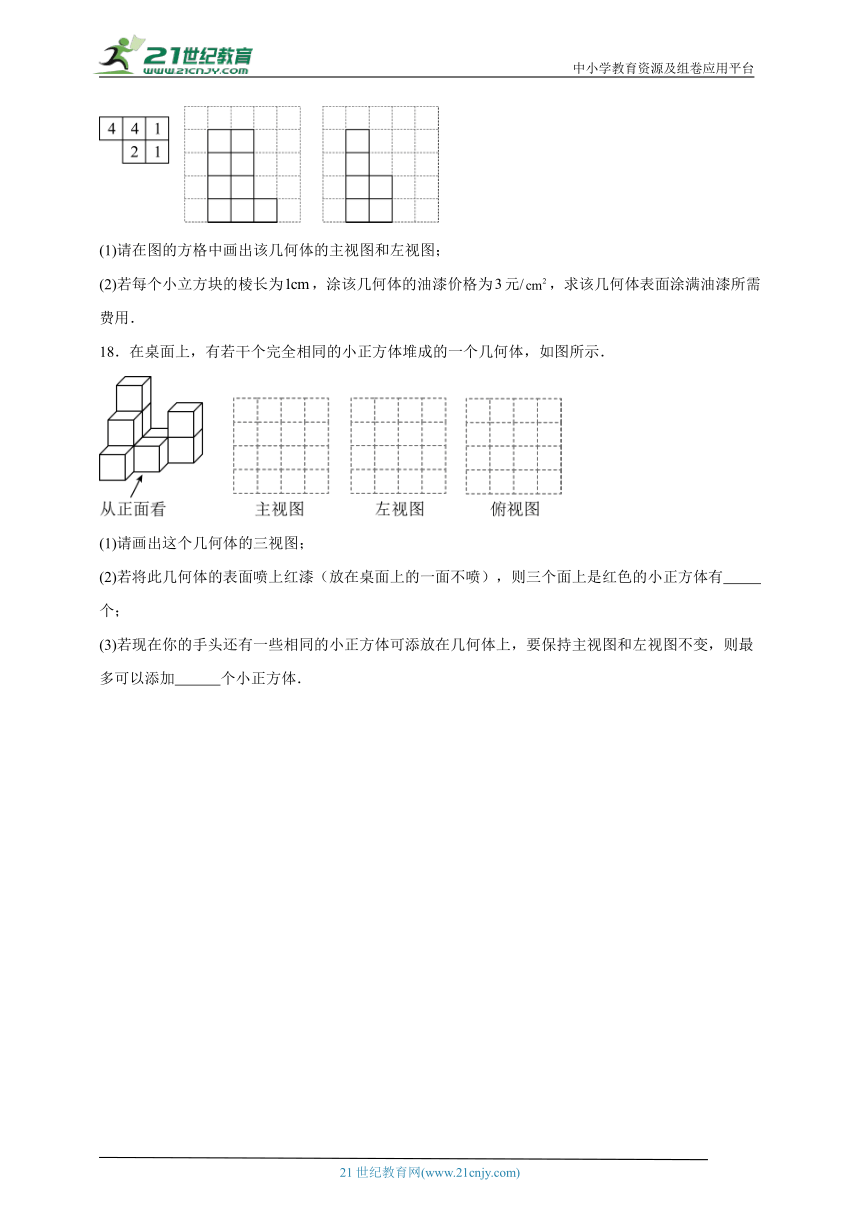
17.一个几何体由大小相同的小立方块搭成,从上面看到的形状如图所示,小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
(1)请在图的方格中画出该几何体的主视图和左视图;
(2)若每个小立方块的棱长为,涂该几何体的油漆价格为元/,求该几何体表面涂满油漆所需费用.
18.在桌面上,有若干个完全相同的小正方体堆成的一个几何体,如图所示.
(1)请画出这个几何体的三视图;
(2)若将此几何体的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个;
(3)若现在你的手头还有一些相同的小正方体可添放在几何体上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
参考答案:
1.B
【分析】本题考查几何体的三视图.做这类题时要借助从不同方向看到的图形表示物体的特点,从正面看的图形上弄清物体的上下和左右形状;从上面看到的图形上弄清物体的左右和前后形状;从左面看到的图形上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.
【详解】解:俯视图中有5个正方形,那么最底层有5个正方体,
由左视图可得第二层有1个正方体,
∴共有个正方体.
故选:B.
2.D
【分析】本题考查三视图:主视图、左视图、俯视图是分别从物体正面、侧面和上面看,所得到的图形.据此逐一判断.注意三视图都相同的常见的几何体有球和正方体.
【详解】解:A.圆柱的主视图和左视图是矩形,俯视图是圆,故本选项不合题意;
B.圆锥的主视图和左视图是等腰三角形,俯视图是带圆心的圆,故本选项不合题意;
C.三棱柱的主视图和左视图是矩形,俯视图是三角形,故本选项不合题意;
D.球的主视图、左视图、俯视图分别为三个全等的圆,故本选项符合题意.
故选:D.
3.A
【分析】本题考查相似三角形的应用.由题意可知在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.经过旗杆在教学楼上的影子的顶端作旗杆的垂线和经过旗杆顶的太阳光线以及旗杆所成三角形,与竹竿,影子光线形成的三角形相似,这样就可求出垂足到旗杆的顶端的高度,再加上墙上的影高就是旗杆高.
【详解】解:设从墙上的影子的顶端到旗杆的顶端的垂直高度是x米.
则有,
解得.
旗杆高是(米).
故选:A.
4.D
【分析】本题考查了中心投影,掌握相似三角形是解题关键.利用相似三角形的性质求解即可.
【详解】解:,
,
,,,
,
,
故选:D.
5.C
【分析】本题考查了简单组合体的三视图,根据从正面看得到的图形是主视图,可得答案.解题的关键是掌握主视图所看的位置.
【详解】解:从正面看,底层是三个小正方形,上层的右边是一个小正方形,
故选:C.
6.A
【分析】本题考查了平行投影,相似三角形的应用:利用影长测量物体的高度.设小雪的身高为,根据在同一时刻物高与影长的比相等得到,然后根据比例性质求x即可.通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
【详解】设小雪的身高为,根据题意得
,
解得.
所以小雪的身高为.
故选A.
7.A
【分析】本题考查了简单组合体的三视图,根据从左边看得到的图形是左视图,可得答案.
【详解】解:从左边看第一层是三个小正方形,第二层中间一个小正方形.
故选:A.
8.D
【分析】本题考查三视图,正方形的性质,长方体的表面积,根据主视图中的数据可得长方体的高和底边正方形的对角线长,进而求出正方形的边长,即可求解.
【详解】解:由图可知,俯视图中正方形的对角线长为,长方体的高为,
正方形的边长为,
这个长方体的表面积为,
故选D.
9.D
【分析】本题考查了简单组合体的三视图,从左边看得到的图形是左视图.根据从左边看得到的图形是左视图,可得答案.
【详解】解:从左边看第一层是两个小正方形,第二层左边一个小正方形,
故选:D.
10.C
【分析】本题考查了由三视图判断几何体,由图可得这个几何体有2层,结合主视图和俯视图可得出第一层和第二层最多的小正方体的个数,由此即可得解,考查了对三视图的掌握和空间想象能力.
【详解】解:由俯视图易得最底层有3个小正方体,第二层最多有2个小正方体,那么搭成这个几何体的小正方体最多为个,
故选:C.
11.1
【分析】本题考查了三视图的画法,根据左视图和俯视图求解即可,综合分析两种视图是解题的关键.
【详解】解:要保持从上面和左面看到的形状图不变,
从左面看:,从上面看:
则从正面看,第二列第二层最多可以拿走1个,
故答案为:1.
12.
【分析】本题主要考查了由三视图判断几何体的知识,解题的关键是利用“三视图”特点找到所需正方体的个数,从左视图中可以看出下面一层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从而确定和的值.
【详解】下面正方体最少的个数应是个,上面正方体最少的个数是个,
∴这个几何体最少有个小正方体组成,即;
下面正方体最多的个数应是个,上面正方体最多的个数是个,
∴这个几何体最多有个小正方体组成,即;
∴,
故答案为:.
13.
【分析】本题考查同一时刻物高和影长成正比.解题的关键是理解:如果光源是太阳,光线是平行照射的,此时物体的高度和影子的长度成正比例.据此列式解答即可.
【详解】解:根据题意知:相同时刻的物高与影长成正比,
设金字塔的高度为米,则:
∴,
解得:,
∴金字塔的高度是米.
故答案为:.
14.10
【分析】此题考查了由三视图判断几何体,根据题意得出左视图的长与宽是解本题的关键.
根据主视图与俯视图的长度,得到左视图的长与宽,即可求出面积.
【详解】解:根据题意得:主视图的长为5,宽为3,俯视图的宽为2,
则左视图的长为5,宽为2,面积为.
故答案为:10.
15.
【分析】本题考查的是平行投影,坡度的含义,如图,延长与的延长线交于 过作于 利用坡度先求解 再利用同一时刻物高与影长成比例求解 从而可得答案.
【详解】解:如图,延长与的延长线交于 过作于
设 则
因为同一时刻测得1米杆在地面上的影长为2米,
而
同理可得:
故答案为:
16.9
【分析】本题考查了由三视图判断几何体,应分别根据主视图、俯视图和左视图综合考虑几何体的形状,体现了对空间想象力的考查.根据题意可以得到该几何体从正面和上面看至少有多少个小立方体,综合考虑即可解答本题.
【详解】解:根据主视图可得俯视图中第一列至少有3层,第二列至少有一处为2层,另一处1层,第三列均为1层,
∴该几何体至少用9个小立方块搭成的.
故答案为:9.
17.(1)见解析;
(2)元.
【分析】本题考查了从不同方向看,几何体表面积,正确理解确定小正方体的个数是解题的关键.
(1)根据从正面看,从左面看的定义,画出即可;
(2)表面积等于上下面的个数即从上面看的图形正方形个数的倍;左右看的正方形面数,前后看的正方形面数,其和乘以一个正方形的面积即可,进而利用表面积乘以单价即可.
【详解】(1)解:
(2)解:∵小正方体的棱长为,
∴每个小正方形的面积为,
∵ ,
∴几何体的上下面的个数为个,前后面的个数为个,左右面的个数为个,
∴几何体表面涂满油漆所需费用为:(元).
18.(1)见解析
(2)2
(3)3
【分析】本题考查了三视图;
(1)由已知条件可知,主视图有3列,每列小正方数形数目分别为3,1,2;左视图有3列,每列小正方形数目分别为3,2,1;俯视图有3列,每列小正方数形数目分别为3,2,1.据此可画出图形;
(2)根据题意,找出三个面是红色的小正方体即可.
(3)根据三视图的定义,解答即可.
【详解】(1)
(2)解:将此几何体的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有2个,分别是主视图中最下一层中间的和左视图中第一列中间的正方体,
故答案为:.
(3)解:如图所示,
最多可添加3个小正方形,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年 人教版(2012)九年级下册 第二十九章 投影与视图 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图是由一些相同的小正方体构成的几何体的左视图和俯视图,这些相同的小正方体的个数为( )
A.5个 B.6个 C.7个 D.8个
2.下列几何体中,其主视图、左视图、右视图完全相同的是( )
A. B. C. D.
3.兴趣小组测量学校的旗杆,在阳光下,甲同学测得长1米的竹竿影长为米,同一时刻乙同学测量时发现旗杆的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,墙壁垂直地面,如图所示,落在墙上的影长为2米,,落在地面上的影长AB为9米,则旗杆的高度是( )米.
A.8 B.12 C. D.
4.如图,小树在路灯O的照射下形成投影.若树高,树影,树与路灯的水平距离.则路灯的高度为( )
A. B. C. D.
5.如图,是一个由6个大小相同的正方体组成的几何体,从正面看这个几何体,得到的图形是( )
A. B.
C. D.
6.中午12点,身高为的小冰的影长为,同学小雪此时在同一地点的影长为,那么小雪的身高为( ).
A. B. C. D.
7.如图是由个相同的小立方块搭成的几何体,那么这个几何体的左视图是( )
A. B. C. D.
8.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为 ( )
A. B. C. D.
9.如图是一个由4个相同的小正方形组成的立体图形,它的左视图是( )
A. B. C. D.
10.由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示,则搭成这个几何体的小正方体的个数最多为( )
A.3个 B.4个 C.5个 D.不能确定
评卷人得分
二、填空题
11.如图所示的几何体由若干个相同的小正方体搭成,要保持从上面和左面看到的形状图不变,最多可以同时拿走 个小正方体.
12.由若干个边长为的小正方体搭成一个组合体,它的主视图、左视图都是如图所示的形状,设垒成这种几何体所需小正方体的个数最少为,最多为,则的值为 .
13.古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔塔顶的影子处直立一根木杆,借助太阳光测金字塔的高度.如图所示,木杆长米.它的影长是米,同一时刻测得是米,则金字塔的高度是 米.
14.如图所示的是从不同方向观察一个长方体得到的视图,则左视图的面积为 .
15.如图,小阳发现电线杆 的影子落在土坡的坡面 和地面 上,量得 米,米,的坡度为:;且此时测得 米杆在地面上的影长为 米,则电线杆的高度为 米.
16.一个几何体由若干个大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是用 个小立方块搭成的.
评卷人得分
三、解答题
17.一个几何体由大小相同的小立方块搭成,从上面看到的形状如图所示,小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
(1)请在图的方格中画出该几何体的主视图和左视图;
(2)若每个小立方块的棱长为,涂该几何体的油漆价格为元/,求该几何体表面涂满油漆所需费用.
18.在桌面上,有若干个完全相同的小正方体堆成的一个几何体,如图所示.
(1)请画出这个几何体的三视图;
(2)若将此几何体的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个;
(3)若现在你的手头还有一些相同的小正方体可添放在几何体上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
参考答案:
1.B
【分析】本题考查几何体的三视图.做这类题时要借助从不同方向看到的图形表示物体的特点,从正面看的图形上弄清物体的上下和左右形状;从上面看到的图形上弄清物体的左右和前后形状;从左面看到的图形上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.
【详解】解:俯视图中有5个正方形,那么最底层有5个正方体,
由左视图可得第二层有1个正方体,
∴共有个正方体.
故选:B.
2.D
【分析】本题考查三视图:主视图、左视图、俯视图是分别从物体正面、侧面和上面看,所得到的图形.据此逐一判断.注意三视图都相同的常见的几何体有球和正方体.
【详解】解:A.圆柱的主视图和左视图是矩形,俯视图是圆,故本选项不合题意;
B.圆锥的主视图和左视图是等腰三角形,俯视图是带圆心的圆,故本选项不合题意;
C.三棱柱的主视图和左视图是矩形,俯视图是三角形,故本选项不合题意;
D.球的主视图、左视图、俯视图分别为三个全等的圆,故本选项符合题意.
故选:D.
3.A
【分析】本题考查相似三角形的应用.由题意可知在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.经过旗杆在教学楼上的影子的顶端作旗杆的垂线和经过旗杆顶的太阳光线以及旗杆所成三角形,与竹竿,影子光线形成的三角形相似,这样就可求出垂足到旗杆的顶端的高度,再加上墙上的影高就是旗杆高.
【详解】解:设从墙上的影子的顶端到旗杆的顶端的垂直高度是x米.
则有,
解得.
旗杆高是(米).
故选:A.
4.D
【分析】本题考查了中心投影,掌握相似三角形是解题关键.利用相似三角形的性质求解即可.
【详解】解:,
,
,,,
,
,
故选:D.
5.C
【分析】本题考查了简单组合体的三视图,根据从正面看得到的图形是主视图,可得答案.解题的关键是掌握主视图所看的位置.
【详解】解:从正面看,底层是三个小正方形,上层的右边是一个小正方形,
故选:C.
6.A
【分析】本题考查了平行投影,相似三角形的应用:利用影长测量物体的高度.设小雪的身高为,根据在同一时刻物高与影长的比相等得到,然后根据比例性质求x即可.通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
【详解】设小雪的身高为,根据题意得
,
解得.
所以小雪的身高为.
故选A.
7.A
【分析】本题考查了简单组合体的三视图,根据从左边看得到的图形是左视图,可得答案.
【详解】解:从左边看第一层是三个小正方形,第二层中间一个小正方形.
故选:A.
8.D
【分析】本题考查三视图,正方形的性质,长方体的表面积,根据主视图中的数据可得长方体的高和底边正方形的对角线长,进而求出正方形的边长,即可求解.
【详解】解:由图可知,俯视图中正方形的对角线长为,长方体的高为,
正方形的边长为,
这个长方体的表面积为,
故选D.
9.D
【分析】本题考查了简单组合体的三视图,从左边看得到的图形是左视图.根据从左边看得到的图形是左视图,可得答案.
【详解】解:从左边看第一层是两个小正方形,第二层左边一个小正方形,
故选:D.
10.C
【分析】本题考查了由三视图判断几何体,由图可得这个几何体有2层,结合主视图和俯视图可得出第一层和第二层最多的小正方体的个数,由此即可得解,考查了对三视图的掌握和空间想象能力.
【详解】解:由俯视图易得最底层有3个小正方体,第二层最多有2个小正方体,那么搭成这个几何体的小正方体最多为个,
故选:C.
11.1
【分析】本题考查了三视图的画法,根据左视图和俯视图求解即可,综合分析两种视图是解题的关键.
【详解】解:要保持从上面和左面看到的形状图不变,
从左面看:,从上面看:
则从正面看,第二列第二层最多可以拿走1个,
故答案为:1.
12.
【分析】本题主要考查了由三视图判断几何体的知识,解题的关键是利用“三视图”特点找到所需正方体的个数,从左视图中可以看出下面一层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从而确定和的值.
【详解】下面正方体最少的个数应是个,上面正方体最少的个数是个,
∴这个几何体最少有个小正方体组成,即;
下面正方体最多的个数应是个,上面正方体最多的个数是个,
∴这个几何体最多有个小正方体组成,即;
∴,
故答案为:.
13.
【分析】本题考查同一时刻物高和影长成正比.解题的关键是理解:如果光源是太阳,光线是平行照射的,此时物体的高度和影子的长度成正比例.据此列式解答即可.
【详解】解:根据题意知:相同时刻的物高与影长成正比,
设金字塔的高度为米,则:
∴,
解得:,
∴金字塔的高度是米.
故答案为:.
14.10
【分析】此题考查了由三视图判断几何体,根据题意得出左视图的长与宽是解本题的关键.
根据主视图与俯视图的长度,得到左视图的长与宽,即可求出面积.
【详解】解:根据题意得:主视图的长为5,宽为3,俯视图的宽为2,
则左视图的长为5,宽为2,面积为.
故答案为:10.
15.
【分析】本题考查的是平行投影,坡度的含义,如图,延长与的延长线交于 过作于 利用坡度先求解 再利用同一时刻物高与影长成比例求解 从而可得答案.
【详解】解:如图,延长与的延长线交于 过作于
设 则
因为同一时刻测得1米杆在地面上的影长为2米,
而
同理可得:
故答案为:
16.9
【分析】本题考查了由三视图判断几何体,应分别根据主视图、俯视图和左视图综合考虑几何体的形状,体现了对空间想象力的考查.根据题意可以得到该几何体从正面和上面看至少有多少个小立方体,综合考虑即可解答本题.
【详解】解:根据主视图可得俯视图中第一列至少有3层,第二列至少有一处为2层,另一处1层,第三列均为1层,
∴该几何体至少用9个小立方块搭成的.
故答案为:9.
17.(1)见解析;
(2)元.
【分析】本题考查了从不同方向看,几何体表面积,正确理解确定小正方体的个数是解题的关键.
(1)根据从正面看,从左面看的定义,画出即可;
(2)表面积等于上下面的个数即从上面看的图形正方形个数的倍;左右看的正方形面数,前后看的正方形面数,其和乘以一个正方形的面积即可,进而利用表面积乘以单价即可.
【详解】(1)解:
(2)解:∵小正方体的棱长为,
∴每个小正方形的面积为,
∵ ,
∴几何体的上下面的个数为个,前后面的个数为个,左右面的个数为个,
∴几何体表面涂满油漆所需费用为:(元).
18.(1)见解析
(2)2
(3)3
【分析】本题考查了三视图;
(1)由已知条件可知,主视图有3列,每列小正方数形数目分别为3,1,2;左视图有3列,每列小正方形数目分别为3,2,1;俯视图有3列,每列小正方数形数目分别为3,2,1.据此可画出图形;
(2)根据题意,找出三个面是红色的小正方体即可.
(3)根据三视图的定义,解答即可.
【详解】(1)
(2)解:将此几何体的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有2个,分别是主视图中最下一层中间的和左视图中第一列中间的正方体,
故答案为:.
(3)解:如图所示,
最多可添加3个小正方形,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
