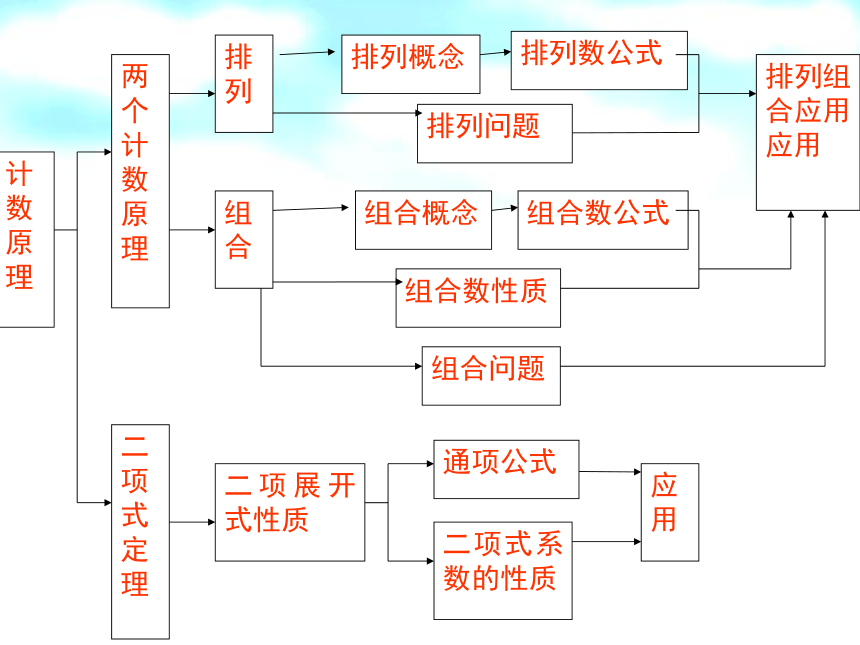
选修2-3第一章复习课

课件17张PPT。选修2-3第一章复习课复习:分类计数原理:定义： 从n个不同元素中取出m(m≤n)个元素
的所有排列的个数,叫做从n个不同元素中取
出m个元素的排列数.
规定：0！=1组合数的定义及其公式： 一般地，从n个不同元素中取出 m(m≤n)个元素合成一组，叫做从n个不同元素中取出 m个元素的一个组合。
组合的定义： 二项式定理 这个公式所表示的定理叫做二项式定理，等号右边的多项式叫做(a+b)n的二项展开式 称为二项展开式的通项公式，它表示展开式的第r+1项.解排列组合问题的常用技巧 （一）特殊元素的“优先安排法” [例1]用0，1，2，3，4这五个数，组成没有重复数字
的三位数，其中偶数共有（ ）
A.24 B.30 C.40 D.60 分析：由于该三位数是偶数，所以末尾数字必须是偶数， 又因为0不能排首位，故0就是其中的“特殊”元素，应优先安排。按0排在末尾和不排在末尾分为两类；0排在末尾时，有 个
0不排在末尾时，有 个
由分类计数原理，共有偶数30个.（2）相邻问题——捆绑法7人站成一排照相，要求甲，乙，丙三人相邻，分别有多少种站法？分析：先将甲，乙，丙三人捆绑在一起看作一个元素，与其余4人共有5个元素做全排列，有 种排法，然后对甲，乙，丙三人进行全排列
由分步计数原理可得：
种不同排法（3）不相邻问题——插空法 对于某几个元素不相邻得排列问题，可先将其它元素排好，然后再将不相邻的元素在已排好的元素之间及两端的空隙之间插入即可。例：7人站成一排照相，要求甲，乙，丙三人不相邻，分别有多少种站法？分析：可先让其余4人站好，共有 种排法，再在这4人之间及两端的5个“空隙”中选三个位置让甲，乙，丙插入，则有 种方法，这样共有 种不同的排法。（4）顺序固定问题用“除法” 对于某几个元素顺序一定的排列问题，可先将这几个元素与其它元素一同进行排列，然后用总的排列数除以这几个元素的全排列数.[例]五人排队，甲在乙前面的排法有几种？分析：若不考虑限制条件，则有 种排法，而甲，乙之间排法有 种，故甲在乙前面的排法只有一种符合条件，故
符合条件的排法有 种.（5）分堆问题例. 6本不同的书分成3堆,各堆分别1，2，3本，则共有多少分法？例. 6本不同的书平均分成3堆,每堆2本共有
多少分法？解：分三步取书得 种方法Why?1 将13个球队分成3组,一组5个队,其它两组4
个队, 有多少分法？2.某校高二年级共有六个班级，现从外地转 入4名学生，要安排到该年级的两个班级且每班安排2名，则不同的安排方案种数为______ 回目录元素相同问题隔板策略例.有10个运动员名额，再分给7个班，每
　　班至少一个,有多少种分配方案？ 解：因为10个名额没有差别，把它们排成
　　一排。相邻名额之间形成９个空隙。在９个空档中选６个位置插个隔板，
可把名额分成７份，对应地分给７个
班级，每一种插板方法对应一种分法
共有___________种分法。在处理排列组合综合题时，通过分析条件按元素的性质分类，做到不重复，不遗漏按事件的发生过程分类、分步，正确地交替使用两个原理，这是解决排列问题的最基本，也是最重要的思想方法。二项式定理有哪些题型？知识梳理：1.两个计数原理：______________(分类)
_______________(分步)2.排列：（1）排列的定义：____________
（2）排列数公式：____________3.组合：（1）组合的定义：__________
（2）组合数公式：____________
（3）组合数性质：①_______②________4.排列组合基本方法：特殊元素法、特殊位置法、捆绑法、插空法、排除法、隔板法、分堆5.排列组合应用题的关键：区别它是排列问题，还是组合问题，也就是看它有无顺序6.二项式定理：______________
通项：_____________7.二项式系数的性质：①对称性_______
②增减性________最大值__________
③二项式系数之和____________8.注意区别“二项式系数”和“项的系数”9.关于二项式定理的类型题：
求展开式、求指定项、求指定项的系数、求二项式系数和、求展开式中指定的项的系数和（赋值法）、整除问题等。