人教版数学七年级下册第九章 不等式与不等式组 学情评估试题(含答案)
文档属性
| 名称 | 人教版数学七年级下册第九章 不等式与不等式组 学情评估试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 18:59:40 | ||
图片预览


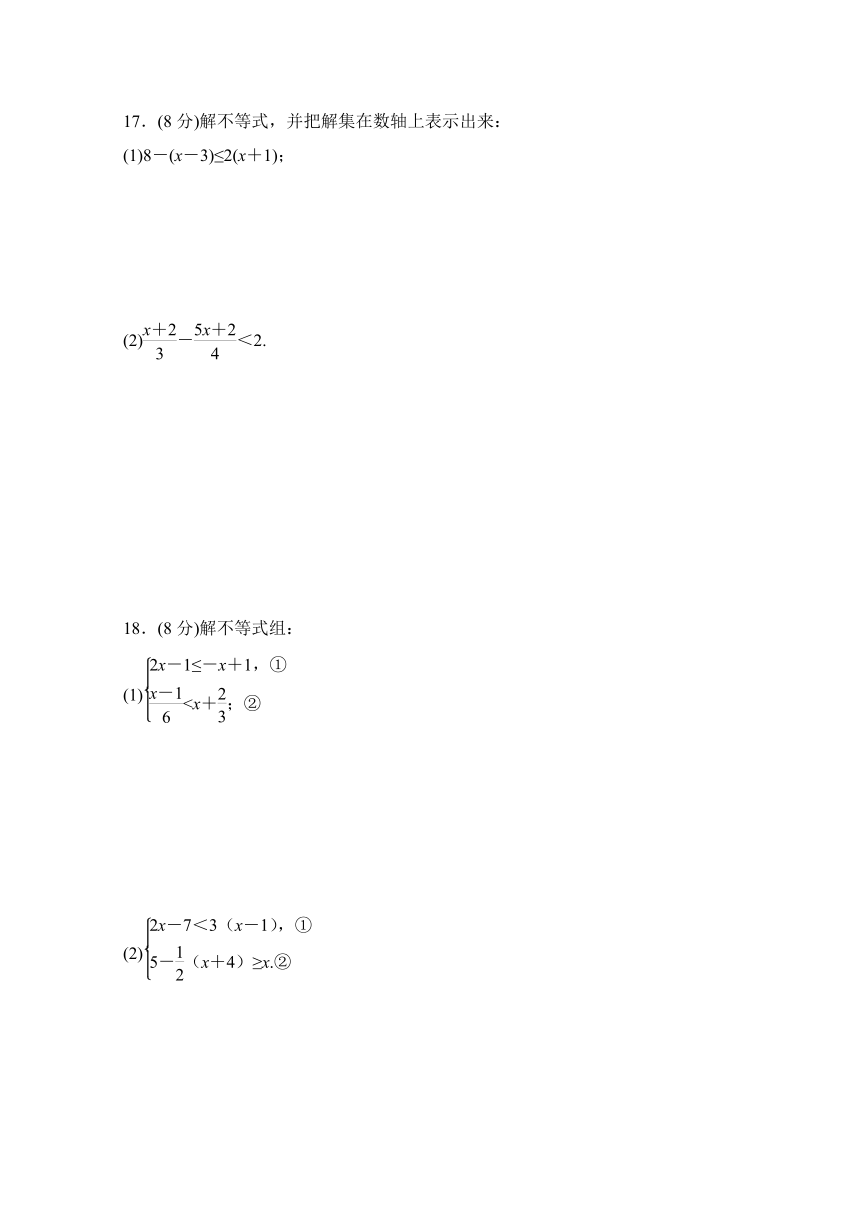

文档简介
第九章学情评估
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列各式中,是一元一次不等式的是( )
A.5+4>8 B.2x-1 C.2x≤5 D.-3x≥0
2.若x>y,则下列式子中错误的是( )
A.x-9>y-9 B.> C.3-x>3-y D.-2x<-2y
3.不等式x+1≥2x-1的解集在数轴上表示为( )
INCLUDEPICTURE"AZ56.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\AZ56.tif" \* MERGEFORMATINET
4.不等式2x-1≤4的最大整数解是( )
A.0 B.1 C. D.2
5.不等式组的解集是( )
A.x≤-2 B.-2≤x< C.x> D.无解
6.已知点P(2a-1,1-a)在第二象限,则a的取值范围是( )
A.a< B.a>1 C.<a<1 D.a<1
7.若关于x的方程x-2+3k=的解是正数,则k的取值范围是( )
A.k> B.k≥ C.k< D.k≤
8.若关于x的不等式组无解,则a的取值范围是( )
A.a≤-3 B.a<-3 C.a>3 D.a≥3
9.八年级某班部分同学去植树,若每人平均植树7棵,则还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设去植树的同学有x人,则下列各项能准确地求出同学人数与种植的树木的数量的是( )
A.7x+9≤8+9(x-1) B.7x+9≥9(x-1)
C. D.
10.甲从商贩A处购买了若干千克西瓜,又从商贩B处购买了若干千克西瓜,A,B两处所购买的西瓜质量之比为3?2,然后将买回的西瓜以从A,B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A.商贩A处西瓜的单价大于商贩B处西瓜的单价
B.商贩A处西瓜的单价等于商贩B处西瓜的单价
C.商贩A处西瓜的单价小于商贩B处西瓜的单价
D.赔钱与商贩A,B处西瓜的单价无关
二、填空题(本题共6小题,每小题3分,共18分)
11.x的与12的差小于6,用不等式表示为______________.
12.若2x+y=1,且013.我校组织开展的环保知识竞赛,共有25道题,规定答对一题得4分,答错或不答扣1分.要使小明参加本次竞赛得分不低于85分,那么他至少要答对________道题.
14.按如图所示的程序进行操作,规定:程序运行从“输入一个数x”到“判断结果是否>7”为一次操作,若经过两次操作就停止,则x的取值范围是____________.
INCLUDEPICTURE"7F-21.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\7F-21.tif" \* MERGEFORMATINET
15.关于x的不等式2x+a≤1只有2个正整数解,则a的取值范围为____________.
16.有这样的一列数:a1,a2,a3,…,an,满足公式an=a1+(n-1)d,已知a2=197,a5=188,若ak>0,ak+1<0,则k的值为____________.
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)解不等式,并把解集在数轴上表示出来:
(1)8-(x-3)≤2(x+1);
(2)-<2.
18.(8分)解不等式组:
(1)
(2)
19.(8分) 为了举行班级晚会,小张同学准备去商店购买20个乒乓球作为道具,并购买一些乒乓球拍作为奖品.已知每个乒乓球1.5元,每副乒乓球拍22元.如果购买金额不超过200元,且购买的球拍数量要尽可能多,那么小张同学应购买多少副球拍?
INCLUDEPICTURE"一改卷+4.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\一改卷+4.tif" \* MERGEFORMATINET
20.(8分)如果点P(x,y)的坐标满足
(1)求点P的坐标;(用含m,n的式子表示x,y)
(2)如果点P在第二象限,且符合要求的整数m只有两个,求n的取值范围;
(3)如果点P在第二象限,且所有符合要求的整数m之和为9,求n的取值范围.
21.(10分)某市为了提升菜篮子工程质量,计划用大、中型车共30辆调拨不超过190吨蔬菜和162吨肉制品补充当地市场.已知一辆大型车可运蔬菜8吨和肉制品5吨;一辆中型车可运蔬菜3吨和肉制品6吨.
(1)符合题意的运输方案有几种?请你帮助设计出来;
(2)若一辆大型车的运费是900元,一辆中型车的运费是600元,(1)中哪种运输方案费用最低?最低费用是多少元?
22.(10分)福州某电器店销售一批进价分别为180元、150元的A,B两种风扇,下表是近两天的销售情况:(利润=销售收入-进货成本)
销售时段 销售数量/台 销售收入/元
A B
第1天 3 5 1560
第2天 4 10 2680
(1)求A,B两种风扇的销售单价;
(2)若该店准备用不多于7 000元的金额再购进这两种风扇共40台.试探索:通过合理安排,销售完这40台风扇能否恰好实现利润1 500元的目标?若能,请给出采购方案;若不能,请说明理由;
(3)若该店按(2)中的方案进货,在实际销售中,为尽快把B种风扇售完,该店决定对B种风扇每台降价a(a为整数)元销售,若全部售完这批风扇利润不低于1 450元,求a的最大值.
答案
一、1.C 2.C 3.B 4.D 5.B 6.A 7.C
8.D 点拨:由题意得a-1≥2,∴a≥3.
9.D 10.A
二、11.x-12<6 12.013.22 14.416.67 点拨:根据题意可得
解得
∴an=200-3(n-1),
∴ak=200-3(k-1)=203-3k,ak+1=200-3k.
∵ak>0,ak+1<0,∴解得66∵k取整数,∴k的值为67.
三、17.解:(1)去括号,得8-x+3≤2x+2,
移项、合并同类项,得-3x≤-9,
系数化为1,得x≥3.
在数轴上表示这个解集如图所示.
INCLUDEPICTURE"7FD-6.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\7FD-6.tif" \* MERGEFORMATINET
(2)去分母,得4(x+2)-3(5x+2)<24,
去括号、移项、合并同类项,得-11x<22,
系数化为1,得x>-2.
在数轴上表示这个解集如图所示.
INCLUDEPICTURE"7FD-7.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\7FD-7.tif" \* MERGEFORMATINET
18.解:(1)由①得x≤;由②得x>-1.
所以原不等式组的解集为-1<x≤.
(2)由①得x>-4;由②得x≤2.
所以原不等式组的解集为-4<x≤2.
19.解:设小张同学购买x副球拍,
依题意,得1.5×20+22x≤200,解得x≤7.
因为x是正整数,所以x的最大值为7.
答:小张同学应购买7副球拍.
20.解:(1)解方程组得
∴点P的坐标为(m-5,m-n).
(2)∵点P在第二象限,
∴∴n<m<5,
∵符合要求的整数m只有两个,∴2≤n<3.
(3)由(2)知n∴m的整数值为-1,0,1,2,3,4或2,3,4,
∴-2≤n<-1或1≤n<2.
21.解:(1)设安排x辆大型车,则安排(30-x)辆中型车.
依题意,得解得18≤x≤20.
因为x为整数,所以x=18,19或20.所以30-x=12,11或10.
所以符合题意的运输方案有3种,方案1:安排18辆大型车,12辆中型车;方案2:安排19辆大型车,11辆中型车;方案3:安排20辆大型车,10辆中型车.
(2)方案1所需费用:900×18+600×12=23 400(元),
方案2所需费用:900×19+600×11=23 700(元),
方案3所需费用:900×20+600×10=24 000(元).
因为23 400<23 700<24 000,
所以方案1所需费用最低,最低费用是23 400元.
22.解:(1)设A种风扇的销售单价为x元,B种风扇的销售单价为y元,
根据题意,得解得
答:A种风扇的销售单价为220元,B种风扇的销售单价为180元.
(2)能.理由如下:设购进A种风扇m台,则购进B种风扇(40-m)台,
根据题意,得180m+150(40-m)≤7 000,
解得m≤33.
因为销售完这40台风扇的利润为1 500元,
所以(220-180)m+(180-150)(40-m)=1 500,
解得m=30.
因为m≤33,所以m=30符合题意.40-m=10.
答:通过合理安排,销售完这40台风扇能恰好实现利润1 500元的目标.采购方案为购进A种风扇30台,B种风扇10台.
(3)根据题意,得30×(220-180)+10×(180-150-a)≥1 450,解得a≤5.所以a的最大值是5.
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列各式中,是一元一次不等式的是( )
A.5+4>8 B.2x-1 C.2x≤5 D.-3x≥0
2.若x>y,则下列式子中错误的是( )
A.x-9>y-9 B.> C.3-x>3-y D.-2x<-2y
3.不等式x+1≥2x-1的解集在数轴上表示为( )
INCLUDEPICTURE"AZ56.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\AZ56.tif" \* MERGEFORMATINET
4.不等式2x-1≤4的最大整数解是( )
A.0 B.1 C. D.2
5.不等式组的解集是( )
A.x≤-2 B.-2≤x< C.x> D.无解
6.已知点P(2a-1,1-a)在第二象限,则a的取值范围是( )
A.a< B.a>1 C.<a<1 D.a<1
7.若关于x的方程x-2+3k=的解是正数,则k的取值范围是( )
A.k> B.k≥ C.k< D.k≤
8.若关于x的不等式组无解,则a的取值范围是( )
A.a≤-3 B.a<-3 C.a>3 D.a≥3
9.八年级某班部分同学去植树,若每人平均植树7棵,则还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设去植树的同学有x人,则下列各项能准确地求出同学人数与种植的树木的数量的是( )
A.7x+9≤8+9(x-1) B.7x+9≥9(x-1)
C. D.
10.甲从商贩A处购买了若干千克西瓜,又从商贩B处购买了若干千克西瓜,A,B两处所购买的西瓜质量之比为3?2,然后将买回的西瓜以从A,B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A.商贩A处西瓜的单价大于商贩B处西瓜的单价
B.商贩A处西瓜的单价等于商贩B处西瓜的单价
C.商贩A处西瓜的单价小于商贩B处西瓜的单价
D.赔钱与商贩A,B处西瓜的单价无关
二、填空题(本题共6小题,每小题3分,共18分)
11.x的与12的差小于6,用不等式表示为______________.
12.若2x+y=1,且0
14.按如图所示的程序进行操作,规定:程序运行从“输入一个数x”到“判断结果是否>7”为一次操作,若经过两次操作就停止,则x的取值范围是____________.
INCLUDEPICTURE"7F-21.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\7F-21.tif" \* MERGEFORMATINET
15.关于x的不等式2x+a≤1只有2个正整数解,则a的取值范围为____________.
16.有这样的一列数:a1,a2,a3,…,an,满足公式an=a1+(n-1)d,已知a2=197,a5=188,若ak>0,ak+1<0,则k的值为____________.
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)解不等式,并把解集在数轴上表示出来:
(1)8-(x-3)≤2(x+1);
(2)-<2.
18.(8分)解不等式组:
(1)
(2)
19.(8分) 为了举行班级晚会,小张同学准备去商店购买20个乒乓球作为道具,并购买一些乒乓球拍作为奖品.已知每个乒乓球1.5元,每副乒乓球拍22元.如果购买金额不超过200元,且购买的球拍数量要尽可能多,那么小张同学应购买多少副球拍?
INCLUDEPICTURE"一改卷+4.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\一改卷+4.tif" \* MERGEFORMATINET
20.(8分)如果点P(x,y)的坐标满足
(1)求点P的坐标;(用含m,n的式子表示x,y)
(2)如果点P在第二象限,且符合要求的整数m只有两个,求n的取值范围;
(3)如果点P在第二象限,且所有符合要求的整数m之和为9,求n的取值范围.
21.(10分)某市为了提升菜篮子工程质量,计划用大、中型车共30辆调拨不超过190吨蔬菜和162吨肉制品补充当地市场.已知一辆大型车可运蔬菜8吨和肉制品5吨;一辆中型车可运蔬菜3吨和肉制品6吨.
(1)符合题意的运输方案有几种?请你帮助设计出来;
(2)若一辆大型车的运费是900元,一辆中型车的运费是600元,(1)中哪种运输方案费用最低?最低费用是多少元?
22.(10分)福州某电器店销售一批进价分别为180元、150元的A,B两种风扇,下表是近两天的销售情况:(利润=销售收入-进货成本)
销售时段 销售数量/台 销售收入/元
A B
第1天 3 5 1560
第2天 4 10 2680
(1)求A,B两种风扇的销售单价;
(2)若该店准备用不多于7 000元的金额再购进这两种风扇共40台.试探索:通过合理安排,销售完这40台风扇能否恰好实现利润1 500元的目标?若能,请给出采购方案;若不能,请说明理由;
(3)若该店按(2)中的方案进货,在实际销售中,为尽快把B种风扇售完,该店决定对B种风扇每台降价a(a为整数)元销售,若全部售完这批风扇利润不低于1 450元,求a的最大值.
答案
一、1.C 2.C 3.B 4.D 5.B 6.A 7.C
8.D 点拨:由题意得a-1≥2,∴a≥3.
9.D 10.A
二、11.x-12<6 12.0
解得
∴an=200-3(n-1),
∴ak=200-3(k-1)=203-3k,ak+1=200-3k.
∵ak>0,ak+1<0,∴解得66
三、17.解:(1)去括号,得8-x+3≤2x+2,
移项、合并同类项,得-3x≤-9,
系数化为1,得x≥3.
在数轴上表示这个解集如图所示.
INCLUDEPICTURE"7FD-6.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\7FD-6.tif" \* MERGEFORMATINET
(2)去分母,得4(x+2)-3(5x+2)<24,
去括号、移项、合并同类项,得-11x<22,
系数化为1,得x>-2.
在数轴上表示这个解集如图所示.
INCLUDEPICTURE"7FD-7.tif" INCLUDEPICTURE "D:\\课件\\七数R福建夹卷\\7FD-7.tif" \* MERGEFORMATINET
18.解:(1)由①得x≤;由②得x>-1.
所以原不等式组的解集为-1<x≤.
(2)由①得x>-4;由②得x≤2.
所以原不等式组的解集为-4<x≤2.
19.解:设小张同学购买x副球拍,
依题意,得1.5×20+22x≤200,解得x≤7.
因为x是正整数,所以x的最大值为7.
答:小张同学应购买7副球拍.
20.解:(1)解方程组得
∴点P的坐标为(m-5,m-n).
(2)∵点P在第二象限,
∴∴n<m<5,
∵符合要求的整数m只有两个,∴2≤n<3.
(3)由(2)知n
∴-2≤n<-1或1≤n<2.
21.解:(1)设安排x辆大型车,则安排(30-x)辆中型车.
依题意,得解得18≤x≤20.
因为x为整数,所以x=18,19或20.所以30-x=12,11或10.
所以符合题意的运输方案有3种,方案1:安排18辆大型车,12辆中型车;方案2:安排19辆大型车,11辆中型车;方案3:安排20辆大型车,10辆中型车.
(2)方案1所需费用:900×18+600×12=23 400(元),
方案2所需费用:900×19+600×11=23 700(元),
方案3所需费用:900×20+600×10=24 000(元).
因为23 400<23 700<24 000,
所以方案1所需费用最低,最低费用是23 400元.
22.解:(1)设A种风扇的销售单价为x元,B种风扇的销售单价为y元,
根据题意,得解得
答:A种风扇的销售单价为220元,B种风扇的销售单价为180元.
(2)能.理由如下:设购进A种风扇m台,则购进B种风扇(40-m)台,
根据题意,得180m+150(40-m)≤7 000,
解得m≤33.
因为销售完这40台风扇的利润为1 500元,
所以(220-180)m+(180-150)(40-m)=1 500,
解得m=30.
因为m≤33,所以m=30符合题意.40-m=10.
答:通过合理安排,销售完这40台风扇能恰好实现利润1 500元的目标.采购方案为购进A种风扇30台,B种风扇10台.
(3)根据题意,得30×(220-180)+10×(180-150-a)≥1 450,解得a≤5.所以a的最大值是5.
